Last time we learned most of the tricks needed to assemble a co-design diagram from the smaller boxes inside: 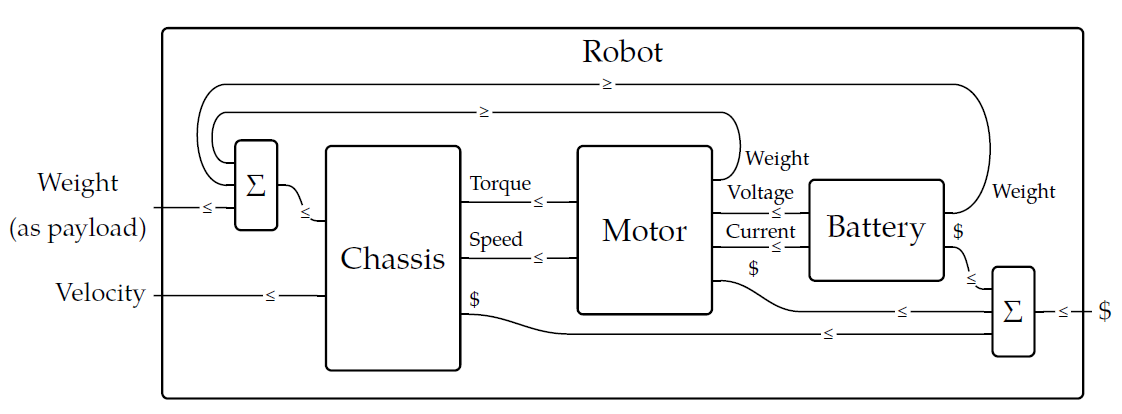Remember, we're really building a feasibility relation out of other feasibility relations. Each smaller box is a feasibility relation. If we don't inquire into exactly what feasibility relations these particular boxes stand for, just how they're assembled, there's just one question left to discuss. What happens when a wire _bends back?_ Intuitively, this describes 'feedback'. For example, I may take some bread, toast it, sell it, make money, and use that to buy more bread. Here I'm stringing together a number of processes, each one producing the resources needed for the next... until finally the last one produces some resources needed for the first! 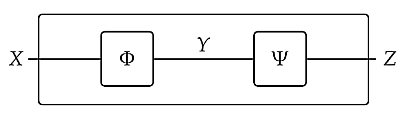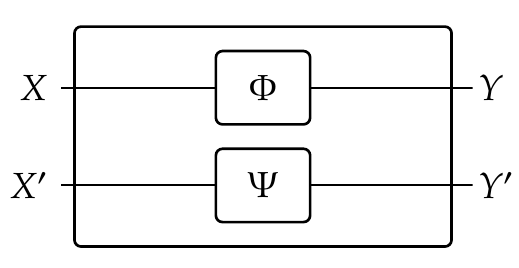It's not obvious how to describe feedback using just **composition**, which takes two feasibility relations \\(\Phi \colon X \nrightarrow Y\\) and \\(\Psi \colon Y \nrightarrow Z\\) and puts one after the other: and **tensoring**, which takes two feasibility relations \\(\Phi \colon X \nrightarrow Y\\) and \\(\Psi \colon X' \nrightarrow Y'\\) and puts them side by side: Using these we can build co-design diagrams like this: 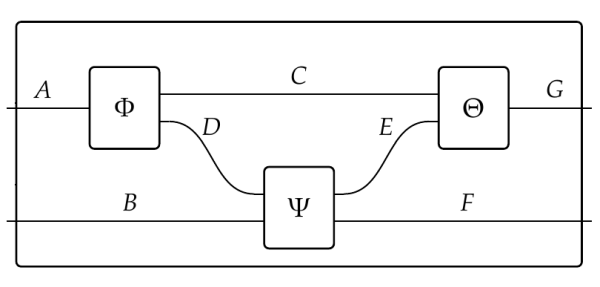But we cannot get wires that bend back! For that we need two extra feasibility relations. The first is called the cup: 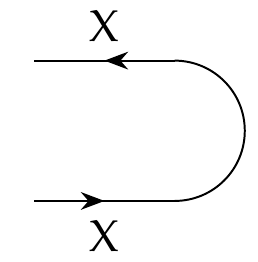It looks like a wire coming in labelled \\(X\\), bending around and going back out to the left. In co-design diagrams, labels of wires stand for preorders. The wire coming in stands for a preorder \\(X\\) as usual. But what about the wire going back out? This stands for \\(X^{\text{op}}\\): the same set with the opposite concept of \\(\le\\). This is a a rule we haven't discussed yet. A wire going from left to right, labelled by some preorder, stands for that preorder. But a wire going right to left, labelled by some preorder stands for the _opposite_ of that preorder. But how do we tell if wire are going from left to right or the other way? One way is to draw arrows on them, as I've done just now. Fong and Spivak often use a different notation: a wire going from left to right is labelled \\(\le\\), while one going the other way is labelled \\(\ge\\). This will turn out to make a lot of sense. Anyway, it looks like our cup stands for a feasibility relation from \\(X^{\text{op}} \times X \\) to... _nothing!_ But what's 'nothing'? That's another rule I haven't told you. 'Nothing' - the invisible wire - is our symbol for the preorder \\(\textbf{1}\\). This is the set \\( \\{0\\} \\) made into a preorder in the only way possible, with \\(0 \le 0\\). So, our cup stands for some particular feasibility relation \[ \cup_X \colon X^{\text{op}} \times X \nrightarrow \textbf{1} . \] Which one? We can guess if remember that such a feasibility relation is really a monotone function \[ \cup_X \colon (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \to \mathbf{Bool} .\] We can simplify this a bit: **Puzzle 213.** Show that for any preorder \\(A\\), the preorder \\( A \times \textbf{1}\\) is **isomorphic** to \\(A\\):: in other words, there is a monotone function from \\( A \times \textbf{1}\\) to \\(A\\) with a monotone inverse. For short we write \\(A \times \textbf{1} \cong A\\). (This is one way in which \\(\textbf{1}\\) acts like 'nothing'.) **Puzzle 214.** Show that for any preorders \\(A\\) and \\(B\\) we have \\( (A \times B)^{\text{op}} \cong A^{\text{op}} \times B^{\text{op}}\\). **Puzzle 215.** Show that for any preorder \\(A\\) we have \\( (A^{\text{op}})^{\text{op}} \cong A\\). So, we get \[ (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \cong (X^{\text{op}} \times X)^\text{op} \cong (X^{\text{op}})^\text{op} \times X^\text{op} \cong X \times X^\text{op} \] Replacing the fancy expression at left by the simpler but isomorphic expression at right, we can reinterpret the cup more simply as a monotone function \[ \cup_X \colon X \times X^{\text{op}} \to \textbf{Bool} . \] What could this be? It should remind you of our old friend the hom-functor \[ \text{hom} \colon X^{\text{op}} \times X \to \textbf{Bool} .\] And that's what it is - just twisted around a bit! In other words, we define \[ \cup_X (x,x') = \text{hom}(x',x) . \] If you forget your old friend the hom-functor, this just means that \[ \cup_X (x,x') = \begin{cases} \texttt{true} & \mbox{if } x' \le x \\\\ \texttt{false} & \mbox{otherwise.} \end{cases} \] Whew! It's simple in the end: it just says that when send a resource round a bend, what comes out must be less than or equal to what came in. 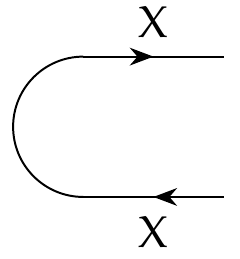The little inequality symbols on this picture are designed to make that easier to remember: One more thing: to describe feedback we also need a feasibility relation called the **cap**, which looks like this: This is some feasibility relation from 'nothing' to \\(X^{\text{op}} \times X\\), or more precisely \[ \cap_X \colon \textbf{1} \nrightarrow X^{\text{op}} \times X .\] **Puzzle 216.** Rewrite this feasibility relation as a monotone function and simplify it just as we did for the cup. Then, guess what it is! The cap winds up being just as simple as the cup. We can discuss this and work it out... and next time I'll show you how to use the cap and cup to describe feedback. By the way, this stuff we're doing was first invented in particle physics. Feynman invented diagrams that describe the interaction between particles... and he realized that an antiparticle could be understood as a particle going 'backwards in time', so he drew little arrows to indicate whether the edges in his diagrams were going forwards or backwards in time. Only much later did people realize that the preorder \\(X^{\text{op}}\\) is like the antiparticle of the preorder \\(X\\). **[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_4)**