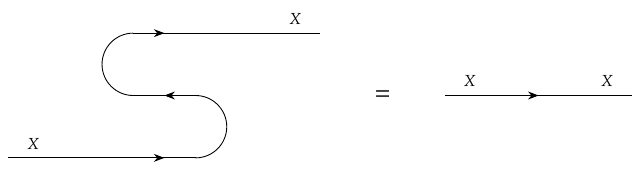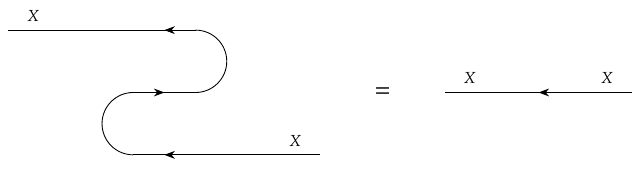[Last time](https://forum.azimuthproject.org/discussion/2303/lecture-67-chapter-4-feedback) we began studying feedback in co-design diagrams. This led us into a fascinating topic which we'll explore more deeply today: cups and caps. Ultimately it leads to the subject of ['compact closed'](https://en.wikipedia.org/wiki/Compact_closed_category) categories, which Fong and Spivak introduce in Section 4.5.1. Covering this material adequately will take longer than the three weeks I'd intended to spend on each chapter, but I think it's worth it.
Last time we saw that for each preorder \\(X\\) there's a feasibility relation called the **cup**
\[ \cup_X \colon X^{\text{op}} \times X \nrightarrow \textbf{1} \]
which we draw as follows:
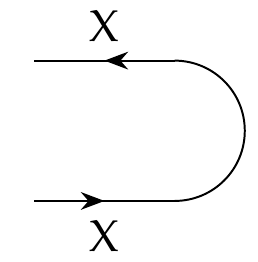 To define the cup, we remembered that feasibility relations \\(X^{\text{op}} \times X \nrightarrow \textbf{1}\\) are monotone functions \\( (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \to \mathbf{Bool} \\), and we defined \\(\cup_X\\) to be the composite
\[ (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \stackrel{\sim}{\to} (X^{\text{op}} \times X)^\text{op} \stackrel{\sim}{\to} (X^{\text{op}})^\text{op} \times X^{\text{op}} \stackrel{\sim}{\to} X \times X^{\text{op}} \stackrel{\sim}{\to} X^{\text{op}} \times X \stackrel{\text{hom}}{\to} \textbf{Bool} \]
where all the arrows with little squiggles over them are isomorphisms - most of them discussed in Puzzles 213-215. In short, the cup is the hom-functor \\(\text{hom} \colon X^{\text{op}} \times X \to \mathbf{Bool}\\) in disguise!
The cup's partner is called the **cap**
\[ \cap_X \colon \textbf{1} \nrightarrow X \times X^{\text{op}} \]
and we draw it like this:
To define the cup, we remembered that feasibility relations \\(X^{\text{op}} \times X \nrightarrow \textbf{1}\\) are monotone functions \\( (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \to \mathbf{Bool} \\), and we defined \\(\cup_X\\) to be the composite
\[ (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \stackrel{\sim}{\to} (X^{\text{op}} \times X)^\text{op} \stackrel{\sim}{\to} (X^{\text{op}})^\text{op} \times X^{\text{op}} \stackrel{\sim}{\to} X \times X^{\text{op}} \stackrel{\sim}{\to} X^{\text{op}} \times X \stackrel{\text{hom}}{\to} \textbf{Bool} \]
where all the arrows with little squiggles over them are isomorphisms - most of them discussed in Puzzles 213-215. In short, the cup is the hom-functor \\(\text{hom} \colon X^{\text{op}} \times X \to \mathbf{Bool}\\) in disguise!
The cup's partner is called the **cap**
\[ \cap_X \colon \textbf{1} \nrightarrow X \times X^{\text{op}} \]
and we draw it like this:
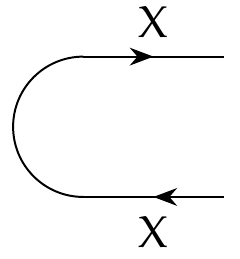 The cap is also the hom-functor in disguise! To define it, remember that feasibility relations \\(\textbf{1} \nrightarrow X^{\text{op}} \times X\\) are monotone functions \\(\textbf{1}^{\text{op}} \times (X^{\text{op}} \times X) \\). But \\(\textbf{1}^{\text{op}} = \textbf{1}\\), so we define the cap to be the compoiste
\[ \textbf{1}^{\text{op}} \times (X^{\text{op}} \times X) = \textbf{1}\times (X^{\text{op}} \times X) \stackrel{\sim}{\to} X^{\text{op}} \times X \stackrel{\text{hom}}{\to} \textbf{Bool} . \]
One great thing about the cup and cap is that they let us treat the edges in our co-design diagrams as flexible wires. In particular, they obey the **snake equations**, also known as the **zig-zag identities**. These say that we can pull taut a zig-zag of wire.
The first snake equation says
The cap is also the hom-functor in disguise! To define it, remember that feasibility relations \\(\textbf{1} \nrightarrow X^{\text{op}} \times X\\) are monotone functions \\(\textbf{1}^{\text{op}} \times (X^{\text{op}} \times X) \\). But \\(\textbf{1}^{\text{op}} = \textbf{1}\\), so we define the cap to be the compoiste
\[ \textbf{1}^{\text{op}} \times (X^{\text{op}} \times X) = \textbf{1}\times (X^{\text{op}} \times X) \stackrel{\sim}{\to} X^{\text{op}} \times X \stackrel{\text{hom}}{\to} \textbf{Bool} . \]
One great thing about the cup and cap is that they let us treat the edges in our co-design diagrams as flexible wires. In particular, they obey the **snake equations**, also known as the **zig-zag identities**. These say that we can pull taut a zig-zag of wire.
The first snake equation says
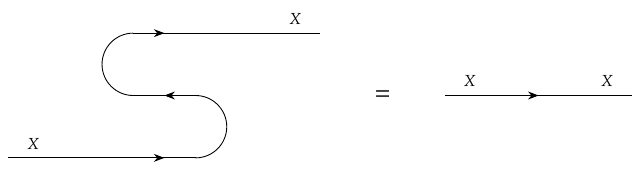 In other words,
\[ (1\_X \times \cup\_X) (\cap\_X \times 1_X)
= 1\_X .\]
Please study the diagram and the corresponding equation very carefully to make sure you see how each part of one corresponds to a part of the other! And please ask questions if there's anything puzzling. It takes a while to get used to these things.
The second snake equation says
In other words,
\[ (1\_X \times \cup\_X) (\cap\_X \times 1_X)
= 1\_X .\]
Please study the diagram and the corresponding equation very carefully to make sure you see how each part of one corresponds to a part of the other! And please ask questions if there's anything puzzling. It takes a while to get used to these things.
The second snake equation says
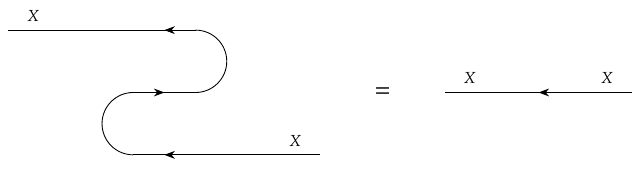 In other words,
\[ (\cup_X \times 1\_{X^{\text{op}}}) (1\_{X^{\text{op}}} \times \cap_X) = 1_{X^{\text{op}}} .\]
A great exercise, to make sure you understand what's going on, is to prove the snake equations. You just need to remember all the definition, use them to compute the left-hand side of the identity, and show it equals the much simpler right-hand side.
**Puzzle 217.** Prove the snake equations.
In fact some of you have already started doing this!
In other words,
\[ (\cup_X \times 1\_{X^{\text{op}}}) (1\_{X^{\text{op}}} \times \cap_X) = 1_{X^{\text{op}}} .\]
A great exercise, to make sure you understand what's going on, is to prove the snake equations. You just need to remember all the definition, use them to compute the left-hand side of the identity, and show it equals the much simpler right-hand side.
**Puzzle 217.** Prove the snake equations.
In fact some of you have already started doing this!