Okay, now we've got all the machinery set up to study co-design diagrams with feedback. Today let's consider a very simple one.
I'll start without feedback. I seem to like examples from business and economics for these purposes:
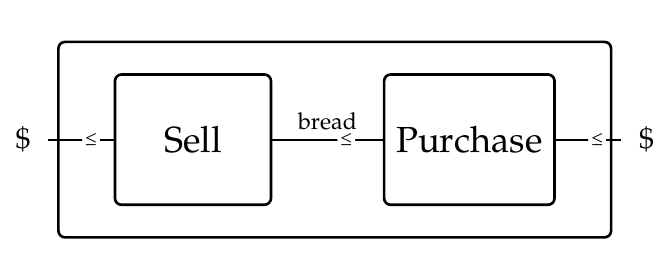 This describes someone who buys bread and then sells it, perhaps at a higher price. This is described by the composite of two feasibility relations:
\[ \mathrm{Purchase} \colon \mathbb{N} \nrightarrow \mathbb{N} \]
and
\[ \mathrm{Sell} \colon \mathbb{N} \nrightarrow \mathbb{N} \]
where \\(\mathbb{N}\\) is the set of natural numbers given its usual ordering \\(\le\\).
Be careful about which way these feasibility relations go:
* \\( \mathrm{Purchase}(j,k) = \texttt{true}\\) if you can purchase \\(j\\) loaves of bread for \\(k\\) dollars.
* \\( \mathrm{Sell}(i,j) = \texttt{true} \\) if you can make \\(i\\) dollars selling \\(j\\) loaves of bread.
The variable at right is the 'resource', while the variable at left describes what you can obtain using this resource. For example, in purchasing bread, \\( \mathrm{Purchase}(j,k) = \text{true}\\) if starting with \\(k\\) dollars as your 'resource' you can buy \\(j\\) loaves of bread. This is an arbitrary convention, but it's the one in the book!
When we compose these we get a feasibility relation
\[ \mathrm{Purchase} \mathrm{Sell} \colon \mathbb{N} \to \mathbb{N} \]
(and again, there's an annoying arbitrary choice of convention in the order here). We have
* \\( (\mathrm{Purchase}\mathrm{Sell})(i,k) = \text{true} \\) if you can make \\(i\\) dollars if you have \\(k\\) dollars to purchase bread which you then sell.
I haven't said what the feasibility relations \\( \mathrm{Purchase}\\) and \\( \mathrm{Sell}\\) actually _are_: they could be all sorts of things. But let's pick something specific, so you can do some computations with them. Let's keep it very simple: let's say you can buy a loaf of bread for \\( \$ 2\\) and sell it for \\( \$ 3\\).
**Puzzle 218.** Write down a formula for the feasibility relation \\(\mathrm{Purchase}.\\)
**Puzzle 219.** Write down a formula for the feasibility relation \\(\mathrm{Sell}.\\)
**Puzzle 220.** Compute the composite feasibility relation \\( \mathrm{Purchase} \mathrm{Sell}\\). (Hint: we discussed composing feasibility relations in [Lecture 58](https://forum.azimuthproject.org/discussion/2283/lecture-58-chapter-4-composing-feasibility-relations/p1).)
That was just a warmup. Now let's introduce feedback!
This describes someone who buys bread and then sells it, perhaps at a higher price. This is described by the composite of two feasibility relations:
\[ \mathrm{Purchase} \colon \mathbb{N} \nrightarrow \mathbb{N} \]
and
\[ \mathrm{Sell} \colon \mathbb{N} \nrightarrow \mathbb{N} \]
where \\(\mathbb{N}\\) is the set of natural numbers given its usual ordering \\(\le\\).
Be careful about which way these feasibility relations go:
* \\( \mathrm{Purchase}(j,k) = \texttt{true}\\) if you can purchase \\(j\\) loaves of bread for \\(k\\) dollars.
* \\( \mathrm{Sell}(i,j) = \texttt{true} \\) if you can make \\(i\\) dollars selling \\(j\\) loaves of bread.
The variable at right is the 'resource', while the variable at left describes what you can obtain using this resource. For example, in purchasing bread, \\( \mathrm{Purchase}(j,k) = \text{true}\\) if starting with \\(k\\) dollars as your 'resource' you can buy \\(j\\) loaves of bread. This is an arbitrary convention, but it's the one in the book!
When we compose these we get a feasibility relation
\[ \mathrm{Purchase} \mathrm{Sell} \colon \mathbb{N} \to \mathbb{N} \]
(and again, there's an annoying arbitrary choice of convention in the order here). We have
* \\( (\mathrm{Purchase}\mathrm{Sell})(i,k) = \text{true} \\) if you can make \\(i\\) dollars if you have \\(k\\) dollars to purchase bread which you then sell.
I haven't said what the feasibility relations \\( \mathrm{Purchase}\\) and \\( \mathrm{Sell}\\) actually _are_: they could be all sorts of things. But let's pick something specific, so you can do some computations with them. Let's keep it very simple: let's say you can buy a loaf of bread for \\( \$ 2\\) and sell it for \\( \$ 3\\).
**Puzzle 218.** Write down a formula for the feasibility relation \\(\mathrm{Purchase}.\\)
**Puzzle 219.** Write down a formula for the feasibility relation \\(\mathrm{Sell}.\\)
**Puzzle 220.** Compute the composite feasibility relation \\( \mathrm{Purchase} \mathrm{Sell}\\). (Hint: we discussed composing feasibility relations in [Lecture 58](https://forum.azimuthproject.org/discussion/2283/lecture-58-chapter-4-composing-feasibility-relations/p1).)
That was just a warmup. Now let's introduce feedback!
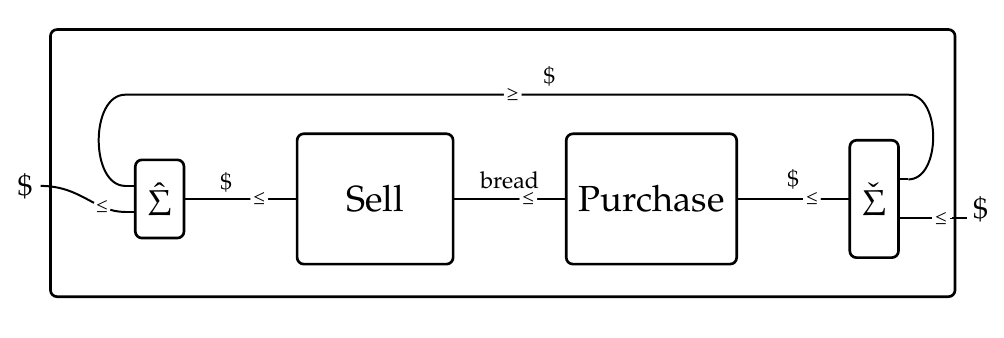 Now you can reinvest some of the money you make to buy more loaves of bread! That creates a 'feedback loop'. Obviously this changes things dramatically: now you can start with a little money and keep making more. But how does the mathematics work now?
First, you'll notice this feedback loop has a cap at left and a cup at right. I defined these [last time](https://forum.azimuthproject.org/discussion/2304/lecture-68-chapter-4-feedback-in-collaborative-design/p1).
But this feedback loop also involves two feasibility relations called \\(\hat{\textstyle{\sum}}\\) and \\(\check{\textstyle{\sum}}\\). We use the one at left,
\[ \hat{\textstyle{\sum}} \colon \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} ,\]
to say that the money we reinvest (which loops back), plus the money we take as profit (which comes out of the diagram at left), equals the money we make by selling bread.
We use the one at right,
\[ \check{\textstyle{\sum}} \colon \mathbb{N} \nrightarrow \mathbb{N} \times \mathbb{N} ,\]
to say that the money we have reinvested (which has looped around), plus the new money we put in (which comes into the diagram at right), equals the money we use to purchase bread.
These two feasibility relations are both built from the monotone function
\[ \textstyle{\sum} \colon \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} \]
defined in the obvious way:
\[ \textstyle{\sum}(m,n) = m + n .\]
Remember, we saw in [Lecture 65](https://forum.azimuthproject.org/discussion/2299/lecture-65-chapter-4-collaborative-design/p1) that any monotone function \\(F \colon \mathcal{X} \to \mathcal{Y} \\) gives two feasibility relations, its 'companion' \\(\hat{F} \colon \mathcal{X} \nrightarrow \mathcal{Y}\\) and its 'conjoint' \\(\check{F} \colon \mathcal{Y} \nrightarrow \mathcal{X}\\).
**Puzzle 221.** Give a formula for the feasibility relation \\( \hat{\textstyle{\sum}} \colon \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} \\). In other words, say when \\(\hat{\textstyle{\sum}}(a,b,c) = \texttt{true}\\).
**Puzzle 222.** Give a formula for the feasibility relation \\( \check{\textstyle{\sum}} \colon \mathbb{N} \nrightarrow \mathbb{N} \times \mathbb{N} \\).
And now finally for the big puzzle that all the others were leading up to:
**Puzzle 223.** Give a formula for the feasibility relation described by this co-design diagram:
Now you can reinvest some of the money you make to buy more loaves of bread! That creates a 'feedback loop'. Obviously this changes things dramatically: now you can start with a little money and keep making more. But how does the mathematics work now?
First, you'll notice this feedback loop has a cap at left and a cup at right. I defined these [last time](https://forum.azimuthproject.org/discussion/2304/lecture-68-chapter-4-feedback-in-collaborative-design/p1).
But this feedback loop also involves two feasibility relations called \\(\hat{\textstyle{\sum}}\\) and \\(\check{\textstyle{\sum}}\\). We use the one at left,
\[ \hat{\textstyle{\sum}} \colon \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} ,\]
to say that the money we reinvest (which loops back), plus the money we take as profit (which comes out of the diagram at left), equals the money we make by selling bread.
We use the one at right,
\[ \check{\textstyle{\sum}} \colon \mathbb{N} \nrightarrow \mathbb{N} \times \mathbb{N} ,\]
to say that the money we have reinvested (which has looped around), plus the new money we put in (which comes into the diagram at right), equals the money we use to purchase bread.
These two feasibility relations are both built from the monotone function
\[ \textstyle{\sum} \colon \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} \]
defined in the obvious way:
\[ \textstyle{\sum}(m,n) = m + n .\]
Remember, we saw in [Lecture 65](https://forum.azimuthproject.org/discussion/2299/lecture-65-chapter-4-collaborative-design/p1) that any monotone function \\(F \colon \mathcal{X} \to \mathcal{Y} \\) gives two feasibility relations, its 'companion' \\(\hat{F} \colon \mathcal{X} \nrightarrow \mathcal{Y}\\) and its 'conjoint' \\(\check{F} \colon \mathcal{Y} \nrightarrow \mathcal{X}\\).
**Puzzle 221.** Give a formula for the feasibility relation \\( \hat{\textstyle{\sum}} \colon \mathbb{N} \times \mathbb{N} \nrightarrow \mathbb{N} \\). In other words, say when \\(\hat{\textstyle{\sum}}(a,b,c) = \texttt{true}\\).
**Puzzle 222.** Give a formula for the feasibility relation \\( \check{\textstyle{\sum}} \colon \mathbb{N} \nrightarrow \mathbb{N} \times \mathbb{N} \\).
And now finally for the big puzzle that all the others were leading up to:
**Puzzle 223.** Give a formula for the feasibility relation described by this co-design diagram:
 You can guess the answer, and then you can work it systematically by composing and tensoring the feasibility relations defined by the boxes, the cap and the cup! This is a good way to make sure you understand everything I've been talking about lately.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_4)**
You can guess the answer, and then you can work it systematically by composing and tensoring the feasibility relations defined by the boxes, the cap and the cup! This is a good way to make sure you understand everything I've been talking about lately.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_4)**


