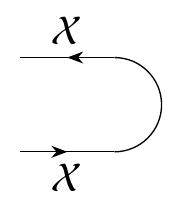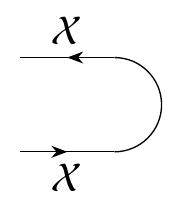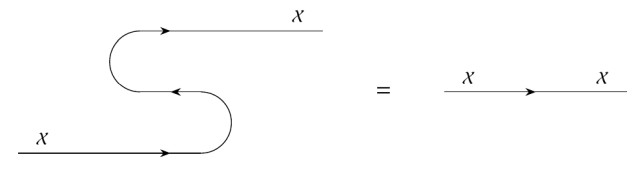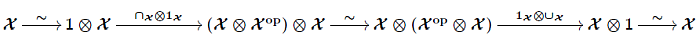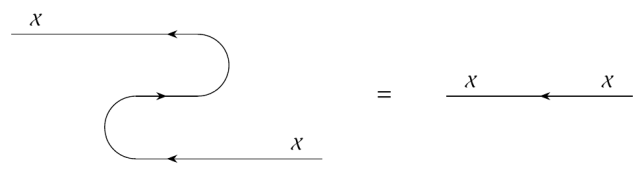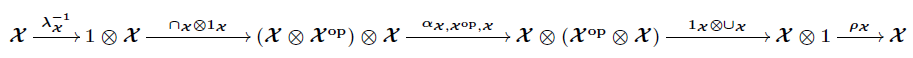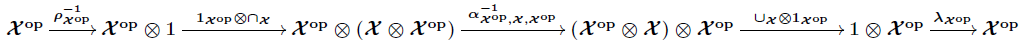Last time we saw how to tensor enriched profunctors. Now let's see caps and cups for enriched profunctors! We are building up to a kind of climax of this course: the theory of 'compact closed categories'. This is the right language for studying many kinds of complex systems, from collaborative design and PERT charts to electrical circuits and control theory. But we need to climb the mountain patiently.
We've already seen caps and cups for feasibility relations in [Lecture 68](https://forum.azimuthproject.org/discussion/2304/lecture-68-chapter-4-feedback-in-collaborative-design/p1). We can just generalize what we did.
As usual, let's assume \\(\mathcal{V}\\) is a commutative quantale, so we get a category \\(\mathbf{Prof}_\mathcal{V}\\) where:
* objects are \\(\mathcal{V}\\)-enriched categories
and
* morphisms are \\(\mathcal{V}\\)-enriched profunctors.
To keep my hands from getting tired, from now on in this lecture I'll simply write 'enriched' when I mean '\\(\mathcal{V}\\)-enriched'.
Let \\(\mathcal{X}\\) be an enriched category. Then there's an enriched profunctor called the **cup**
\[ \cup_{\mathcal{X}} \colon \mathcal{X}^{\text{op}} \otimes \mathcal{X} \nrightarrow \textbf{1} \]
drawn as follows:
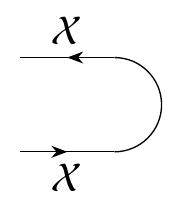 To define it, remember that enriched profunctors \\(\mathcal{X}^{\text{op}} \otimes \mathcal{X} \nrightarrow \textbf{1}\\) are really just enriched functors \\( (\mathcal{X}^{\text{op}} \otimes \mathcal{X})^\text{op} \otimes \textbf{1} \to \mathcal{V} \\). Also, remember that \\(\mathcal{X}\\) comes with a **hom-functor**, which is the enriched functor
\[ \mathrm{hom} \colon \mathcal{X}^{\text{op}} \otimes \mathcal{X} \to \mathcal{V} \]
sending any object \\( (x,x') \\) to \\( \mathcal{X}(x,x')\\). So, we define \\(\cup_\mathcal{X}\\) to be the composite
\[ (\mathcal{X}^{\text{op}} \otimes \mathcal{X})^\text{op} \otimes \textbf{1} \stackrel{\sim}{\to} (\mathcal{X}^{\text{op}} \otimes \mathcal{X})^\text{op} \stackrel{\sim}{\to} (\mathcal{X}^{\text{op}})^\text{op} \otimes \mathcal{X}^{\text{op}} \stackrel{\sim}{\to} \mathcal{X} \otimes \mathcal{X}^{\text{op}} \stackrel{\sim}{\to} \mathcal{X}^{\text{op}} \otimes \mathcal{X} \stackrel{\text{hom}}{\to} \mathcal{V} \]
where the arrows with squiggles over them are isomorphisms, most of which I explained [last time](https://forum.azimuthproject.org/discussion/2310/lecture-70-tensoring-enriched-profunctors/p1).
There's also an enriched profunctor called the **cap**
\[ \cap_\mathcal{X} \colon \textbf{1} \nrightarrow \mathcal{X} \otimes \mathcal{X}^{\text{op}} \]
drawn like this:
To define it, remember that enriched profunctors \\(\mathcal{X}^{\text{op}} \otimes \mathcal{X} \nrightarrow \textbf{1}\\) are really just enriched functors \\( (\mathcal{X}^{\text{op}} \otimes \mathcal{X})^\text{op} \otimes \textbf{1} \to \mathcal{V} \\). Also, remember that \\(\mathcal{X}\\) comes with a **hom-functor**, which is the enriched functor
\[ \mathrm{hom} \colon \mathcal{X}^{\text{op}} \otimes \mathcal{X} \to \mathcal{V} \]
sending any object \\( (x,x') \\) to \\( \mathcal{X}(x,x')\\). So, we define \\(\cup_\mathcal{X}\\) to be the composite
\[ (\mathcal{X}^{\text{op}} \otimes \mathcal{X})^\text{op} \otimes \textbf{1} \stackrel{\sim}{\to} (\mathcal{X}^{\text{op}} \otimes \mathcal{X})^\text{op} \stackrel{\sim}{\to} (\mathcal{X}^{\text{op}})^\text{op} \otimes \mathcal{X}^{\text{op}} \stackrel{\sim}{\to} \mathcal{X} \otimes \mathcal{X}^{\text{op}} \stackrel{\sim}{\to} \mathcal{X}^{\text{op}} \otimes \mathcal{X} \stackrel{\text{hom}}{\to} \mathcal{V} \]
where the arrows with squiggles over them are isomorphisms, most of which I explained [last time](https://forum.azimuthproject.org/discussion/2310/lecture-70-tensoring-enriched-profunctors/p1).
There's also an enriched profunctor called the **cap**
\[ \cap_\mathcal{X} \colon \textbf{1} \nrightarrow \mathcal{X} \otimes \mathcal{X}^{\text{op}} \]
drawn like this:
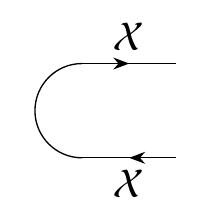 To define this, remember that enriched profunctors \\(\textbf{1} \nrightarrow \mathcal{X} \otimes \mathcal{X}^{\text{op}} \\) are enriched profunctors \\(\textbf{1}^{\text{op}} \otimes (\mathcal{X} \otimes \mathcal{X}^{\text{op}}) \\). But \\(\textbf{1}^{\text{op}} = \textbf{1}\\), so we define the cap to be the composite
\[ \textbf{1}^{\text{op}} \otimes (\mathcal{X} \otimes \mathcal{X}^{\text{op}}) = \textbf{1}\otimes (\mathcal{X} \otimes \mathcal{X}^{\text{op}}) \stackrel{\sim}{\to} \mathcal{X} \otimes \mathcal{X}^{\text{op}} \stackrel{\sim}{\to} \mathcal{X}^{\text{op}} \otimes \mathcal{X} \stackrel{\text{hom}}{\to} \mathcal{V} . \]
As we've already seen for feasibility relations, the cap and cup obey the **snake equations**, also known as **zig-zag equations** or **yanking equations**. (Everyone likes making up their own poetic names for these equations.) The first snake equation says
To define this, remember that enriched profunctors \\(\textbf{1} \nrightarrow \mathcal{X} \otimes \mathcal{X}^{\text{op}} \\) are enriched profunctors \\(\textbf{1}^{\text{op}} \otimes (\mathcal{X} \otimes \mathcal{X}^{\text{op}}) \\). But \\(\textbf{1}^{\text{op}} = \textbf{1}\\), so we define the cap to be the composite
\[ \textbf{1}^{\text{op}} \otimes (\mathcal{X} \otimes \mathcal{X}^{\text{op}}) = \textbf{1}\otimes (\mathcal{X} \otimes \mathcal{X}^{\text{op}}) \stackrel{\sim}{\to} \mathcal{X} \otimes \mathcal{X}^{\text{op}} \stackrel{\sim}{\to} \mathcal{X}^{\text{op}} \otimes \mathcal{X} \stackrel{\text{hom}}{\to} \mathcal{V} . \]
As we've already seen for feasibility relations, the cap and cup obey the **snake equations**, also known as **zig-zag equations** or **yanking equations**. (Everyone likes making up their own poetic names for these equations.) The first snake equation says
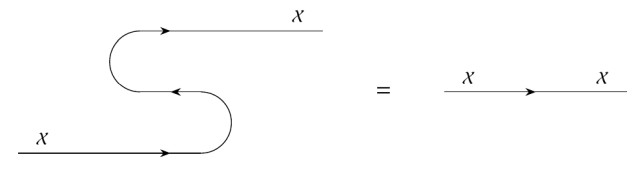 In other words, the composite
In other words, the composite
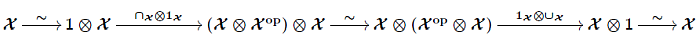 is the identity, where the arrows with squiggles over them are obvious isomorphisms that I described [last time](https://forum.azimuthproject.org/discussion/2310/lecture-70-tensoring-enriched-profunctors/p1). The second snake equation says
is the identity, where the arrows with squiggles over them are obvious isomorphisms that I described [last time](https://forum.azimuthproject.org/discussion/2310/lecture-70-tensoring-enriched-profunctors/p1). The second snake equation says
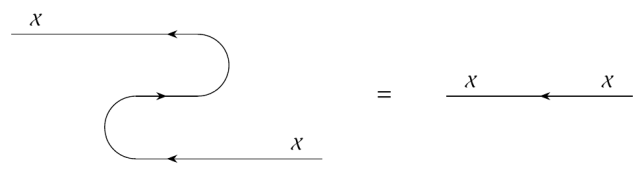 In other words, the composite
In other words, the composite
 is the identity.
Last time I sketched how \\(\mathbf{Prof}_{\mathcal{V}}\\) is a [monoidal](https://en.wikipedia.org/wiki/Monoidal_category) category, meaning one with a tensor product obeying certain rules. It's also [symmetric monoidal](https://en.wikipedia.org/wiki/Symmetric_monoidal_category), meaning it has isomorphisms
\[ \sigma_{\mathcal{X}, \mathcal{Y}} \colon \mathcal{X} \otimes \mathcal{Y} \nrightarrow \mathcal{Y} \otimes \mathcal{X} \]
obeying certain rules. These let us switch the order of objects in a tensor product: in terms of diagrams, it means wires can cross each other! And finally, when every object in a symmetric monoidal category has a cap and cup obeying the snake equations, we say that category is [compact closed](https://en.wikipedia.org/wiki/Compact_closed_category). I will define all these concepts more carefully soon. For now I just want you to know that
_Compact closed categories let us study processes that can run in series or in parallel, with feedback_.
and also that \\(\mathbf{Prof}_{\mathcal{V}}\\) is an example of a compact closed category. If you're impatient to learn more, try Section 4.4 of the book.
**Puzzle 227.** Prove the snake equations in \\(\mathbf{Prof}_{\mathcal{V}}\\).
For this, I should state the snake equations more precisely! The first one says this composite:
is the identity.
Last time I sketched how \\(\mathbf{Prof}_{\mathcal{V}}\\) is a [monoidal](https://en.wikipedia.org/wiki/Monoidal_category) category, meaning one with a tensor product obeying certain rules. It's also [symmetric monoidal](https://en.wikipedia.org/wiki/Symmetric_monoidal_category), meaning it has isomorphisms
\[ \sigma_{\mathcal{X}, \mathcal{Y}} \colon \mathcal{X} \otimes \mathcal{Y} \nrightarrow \mathcal{Y} \otimes \mathcal{X} \]
obeying certain rules. These let us switch the order of objects in a tensor product: in terms of diagrams, it means wires can cross each other! And finally, when every object in a symmetric monoidal category has a cap and cup obeying the snake equations, we say that category is [compact closed](https://en.wikipedia.org/wiki/Compact_closed_category). I will define all these concepts more carefully soon. For now I just want you to know that
_Compact closed categories let us study processes that can run in series or in parallel, with feedback_.
and also that \\(\mathbf{Prof}_{\mathcal{V}}\\) is an example of a compact closed category. If you're impatient to learn more, try Section 4.4 of the book.
**Puzzle 227.** Prove the snake equations in \\(\mathbf{Prof}_{\mathcal{V}}\\).
For this, I should state the snake equations more precisely! The first one says this composite:
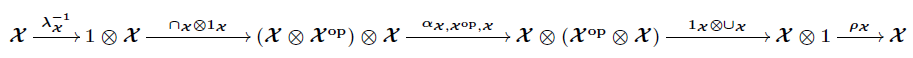 is the identity, where \\(\alpha\\) is the associator and \\(\lambda, \rho\\) are the left and right unitors, defined [last time](https://forum.azimuthproject.org/discussion/2310/lecture-70-tensoring-enriched-profunctors/p1). The second snake equation says this composite:
is the identity, where \\(\alpha\\) is the associator and \\(\lambda, \rho\\) are the left and right unitors, defined [last time](https://forum.azimuthproject.org/discussion/2310/lecture-70-tensoring-enriched-profunctors/p1). The second snake equation says this composite:
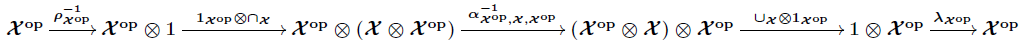 is the identity.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_4)**
is the identity.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_4)**