We can use the math we've been developing to answer the question "given what I have, is it possible to get what I want?" For example, consider a set \\(S\\) of different resources:
* crust
* lemon
* (one stick of) butter
* (one cup of) sugar
* egg
* yolk
* white
* (lemon) filling
* meringue
* (unbaked) lemon pie
* (unbaked) meringue pie
Then there is a monoid called \\(\mathbb{N}[S]\\) consisting of combinations of these things, like
\[ 2 [\textrm{crust}] + 3[\textrm{egg}] + 2[\textrm{filling}] .\]
We write the operation in this monoid as \\(+\\), and it's commutative. For example:
\[ 2 [\textrm{egg}] + [\textrm{yolk}] = [\textrm{yolk}] + 2 [\textrm{egg}] .\]
The coefficients in front of the various things say how many copies of them we have, and addition works with these in the obvious way; for example:
\[ (2 [\textrm{egg}] + [\textrm{yolk}]) + (3 [\textrm{egg}] + 3 [\textrm{crust}]) = 5[\textrm{egg}] + [\textrm{yolk}] + 3 [\textrm{crust}] . \]
Also, this monoid has an element \\(0\\) which serves as the identity for addition: it corresponds to _nothing_. For example:
\[ [\textrm{egg}] + 0 = [\textrm{egg}] .\]
This monoid is called \\(\mathbb{N}[S]\\) because it consists of linear combinations of things in \\(S\\) with _natural number_ coefficients. So, we are not allowing ourselves to talk about \\( \frac{1}{2} [\textrm{stick of butter}] \\) or \\( -3 [\textrm{egg}] \\). Why not? Simple: while those generalizations are important, they're not part of the game we're playing right now.
Next we need to decide which combinations of things we can turn into which other combinations of things. As explained in [Lecture 19](https://forum.azimuthproject.org/discussion/2079/lecture-19-chapter-2-chemistry-and-scheduling/p1), we can specify this using a [Petri net](https://en.wikipedia.org/wiki/Petri_net):
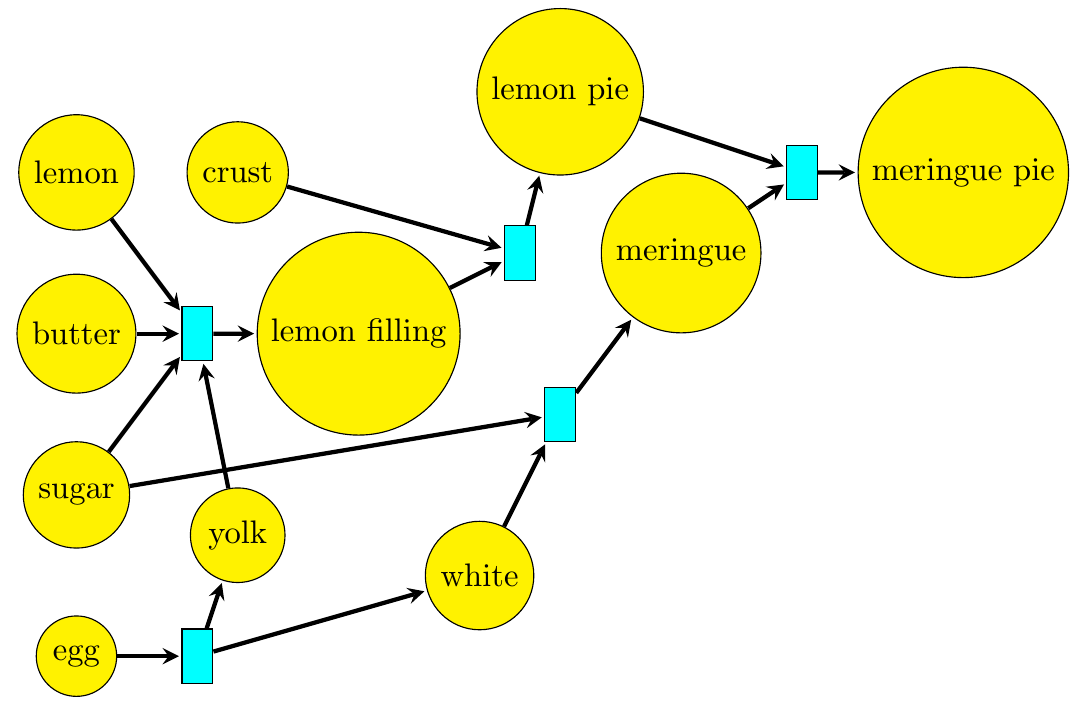 Another way to present the same information is to write down a **[reaction network](https://en.wikipedia.org/wiki/Chemical_reaction_network_theory#Overview).** This is a bunch of reactions going between elements of \\(\mathbb{N}[S]\\), like this:
\[ [\textrm{egg}] \to [\textrm{yolk}] + [\textrm{white}] \]
\[ [\textrm{lemon}] + [\text{butter}] + [\text{sugar}] + [\text{yolk}] \to [\textrm{filling}] \]
\[ [\textrm{crust}] + [\textrm{filling}] \to [\textrm{lemon pie}] \]
\[ [\textrm{white}] + [\textrm{sugar}] \to [\textrm{meringue}] \]
\[ [\textrm{lemon pie}] + [\textrm{meringue}] \to [\textrm{meringue pie}] \]
We can also think of these reactions as _inequalities_, which we use to make our monoid \\(\mathbb{N}[S]\\) into a monoidal preorder! I've been using the convention that says \\(x \le y\\) if we can make \\(x\\) from \\(y\\). The book uses the opposite convention. Both have their advantages, and I keep wanting to flip-flop, like right now - but all that really matters is to stay consistent. With my convention, the reaction network above gives these inequalities:
\[ [\textrm{yolk}] + [\textrm{white}] \le [\textrm{egg}] \]
\[ [\textrm{lemon filling}] \le [\textrm{lemon}] + [\text{butter}] + [\text{sugar}] + [\text{yolk}] \]
\[ [\textrm{lemon pie}] \le [\textrm{crust}] + [\textrm{filling}] \]
\[ [\textrm{meringue}] \le [\textrm{white}] + [\textrm{sugar}] \]
\[ [\textrm{meringue pie}] \le [\textrm{lemon pie}] + [\textrm{meringue}] \]
We can then reason with these inequalities using the laws of a symmetric monoidal preorder - in fact a commutative one! So, we can use these 6 laws:
* reflexivity: \\(x \le x\\)
* transitivity: \\(x \le y\\) and \\(y \le z\\) imply \\(x \le z\\)
* associativity: \\( x + (y + z) = (x + y) + z \\)
* the left and right unit laws: \\( 0 + x = x = x + 0 \\)
* commutativity: \\(x + y = y + x \\)
* the monoidal preorder law: \\(x \le x'\\) and \\(y \le y'\\) imply \\(x + y \le x' + y'\\).
So, since we have
\[ [\textrm{yolk}] + [\textrm{white}] \le [\textrm{egg}] \]
and
\[ [\textrm{meringue}] \le [\textrm{white}] + [\textrm{sugar}] \]
we can add a cup of sugar to both sides of the first inequality, using reflexivity and the monoidal preorder law:
\[ [\textrm{yolk}] + [\textrm{white}] + [\textrm{sugar}] \le [\textrm{egg}] + [\textrm{sugar}] \]
and add a yolk to the second inequality, in the same way:
\[ [\textrm{yolk}] + [\textrm{meringue}] \le [\textrm{yolk}] + [\textrm{white}] + [\textrm{sugar}] \]
Then we can string together the resulting inequalities using transitivity:
\[ [\textrm{yolk}] + [\textrm{meringue}] \le [\textrm{egg}] + [\textrm{sugar}] \]
and so on.
Indeed, such reasoning lets you prove it's possible to make a lemon meringue pie from suitable ingredients:
\[ [\textrm{meringue pie}] \le [\textrm{crust}] + [\textrm{lemon}] + 2[\textrm{sugar}] + [\textrm{butter}] + [\textrm{egg}] . \]
We can also prove such facts using "wiring diagrams", as mentioned in [Lecture 18](https://forum.azimuthproject.org/discussion/2075/lecture-18-chapter-2-resource-theories/p1):
Another way to present the same information is to write down a **[reaction network](https://en.wikipedia.org/wiki/Chemical_reaction_network_theory#Overview).** This is a bunch of reactions going between elements of \\(\mathbb{N}[S]\\), like this:
\[ [\textrm{egg}] \to [\textrm{yolk}] + [\textrm{white}] \]
\[ [\textrm{lemon}] + [\text{butter}] + [\text{sugar}] + [\text{yolk}] \to [\textrm{filling}] \]
\[ [\textrm{crust}] + [\textrm{filling}] \to [\textrm{lemon pie}] \]
\[ [\textrm{white}] + [\textrm{sugar}] \to [\textrm{meringue}] \]
\[ [\textrm{lemon pie}] + [\textrm{meringue}] \to [\textrm{meringue pie}] \]
We can also think of these reactions as _inequalities_, which we use to make our monoid \\(\mathbb{N}[S]\\) into a monoidal preorder! I've been using the convention that says \\(x \le y\\) if we can make \\(x\\) from \\(y\\). The book uses the opposite convention. Both have their advantages, and I keep wanting to flip-flop, like right now - but all that really matters is to stay consistent. With my convention, the reaction network above gives these inequalities:
\[ [\textrm{yolk}] + [\textrm{white}] \le [\textrm{egg}] \]
\[ [\textrm{lemon filling}] \le [\textrm{lemon}] + [\text{butter}] + [\text{sugar}] + [\text{yolk}] \]
\[ [\textrm{lemon pie}] \le [\textrm{crust}] + [\textrm{filling}] \]
\[ [\textrm{meringue}] \le [\textrm{white}] + [\textrm{sugar}] \]
\[ [\textrm{meringue pie}] \le [\textrm{lemon pie}] + [\textrm{meringue}] \]
We can then reason with these inequalities using the laws of a symmetric monoidal preorder - in fact a commutative one! So, we can use these 6 laws:
* reflexivity: \\(x \le x\\)
* transitivity: \\(x \le y\\) and \\(y \le z\\) imply \\(x \le z\\)
* associativity: \\( x + (y + z) = (x + y) + z \\)
* the left and right unit laws: \\( 0 + x = x = x + 0 \\)
* commutativity: \\(x + y = y + x \\)
* the monoidal preorder law: \\(x \le x'\\) and \\(y \le y'\\) imply \\(x + y \le x' + y'\\).
So, since we have
\[ [\textrm{yolk}] + [\textrm{white}] \le [\textrm{egg}] \]
and
\[ [\textrm{meringue}] \le [\textrm{white}] + [\textrm{sugar}] \]
we can add a cup of sugar to both sides of the first inequality, using reflexivity and the monoidal preorder law:
\[ [\textrm{yolk}] + [\textrm{white}] + [\textrm{sugar}] \le [\textrm{egg}] + [\textrm{sugar}] \]
and add a yolk to the second inequality, in the same way:
\[ [\textrm{yolk}] + [\textrm{meringue}] \le [\textrm{yolk}] + [\textrm{white}] + [\textrm{sugar}] \]
Then we can string together the resulting inequalities using transitivity:
\[ [\textrm{yolk}] + [\textrm{meringue}] \le [\textrm{egg}] + [\textrm{sugar}] \]
and so on.
Indeed, such reasoning lets you prove it's possible to make a lemon meringue pie from suitable ingredients:
\[ [\textrm{meringue pie}] \le [\textrm{crust}] + [\textrm{lemon}] + 2[\textrm{sugar}] + [\textrm{butter}] + [\textrm{egg}] . \]
We can also prove such facts using "wiring diagrams", as mentioned in [Lecture 18](https://forum.azimuthproject.org/discussion/2075/lecture-18-chapter-2-resource-theories/p1):
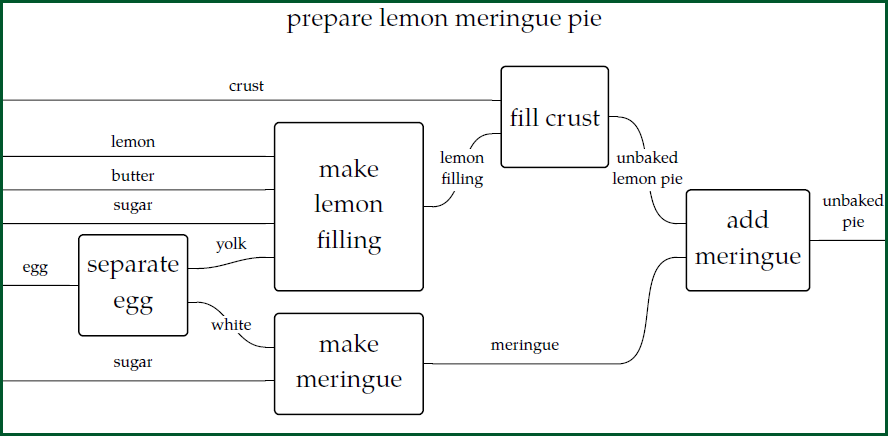 Here each basic inequality is drawn as a little box, and we combine them to prove more complicated inequalities. It's sort of an obvious idea. But how does it work, exactly? How, exactly, do our 6 rules for a commutative monoidal preorder turn into tricks we can play with wiring diagrams? I'll let you think about this:
**Puzzle 78.** When we reason using transitivity:
\\(x \le y\\) and \\(y \le z\\) imply \\(x \le z\\)
what does this look like in terms of wiring diagrams?
**Puzzle 79.** When we reason using the monoidal preorder law:
\\(x \le x'\\) and \\(y \le y'\\) imply \\(x + y \le x' + y'\\)
what does this look like in terms of wiring diagrams?
We could go through all 6 laws this way, but those two are the most charismatic in terms of pictures. You should read Section 2.2.2 of [the book](http://math.mit.edu/~dspivak/teaching/sp18/7Sketches.pdf) to learn more about wiring diagrams and the rules for working with them.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2)**
Here each basic inequality is drawn as a little box, and we combine them to prove more complicated inequalities. It's sort of an obvious idea. But how does it work, exactly? How, exactly, do our 6 rules for a commutative monoidal preorder turn into tricks we can play with wiring diagrams? I'll let you think about this:
**Puzzle 78.** When we reason using transitivity:
\\(x \le y\\) and \\(y \le z\\) imply \\(x \le z\\)
what does this look like in terms of wiring diagrams?
**Puzzle 79.** When we reason using the monoidal preorder law:
\\(x \le x'\\) and \\(y \le y'\\) imply \\(x + y \le x' + y'\\)
what does this look like in terms of wiring diagrams?
We could go through all 6 laws this way, but those two are the most charismatic in terms of pictures. You should read Section 2.2.2 of [the book](http://math.mit.edu/~dspivak/teaching/sp18/7Sketches.pdf) to learn more about wiring diagrams and the rules for working with them.
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_2)**

