We've been having fun with databases using categories and functors. To go any further we need 'natural transformations'. These are one of the most important aspects of category theory. They give it a special flavor different from almost all previous branches of mathematics!
In most branches of math you study _gadgets_ and _maps between gadgets_, like:
* sets and functions between sets,
* vector spaces and linear maps between vector spaces,
* posets and monotone functions between posets,
and so on.
We do this in category theory too! We have categories and functors between categories. But category theory has an extra layer. It also has _natural transformations between functors._
The reason is not hard to find. Some people think categories are abstract, but I don't. When you say the word 'category', a picture sort of like this pops into my head:
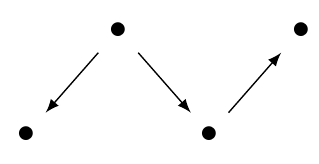 It's a bunch of objects, which look like dots, and a bunch of morphisms, which look like arrows between dots.
Now, you might object that this is a picture of a _graph_, not a category. And you'd be right! In a category we can _compose_ morphisms, and we also have _identity_ morphisms. So a more detailed mental picture of the same category would look like this:
It's a bunch of objects, which look like dots, and a bunch of morphisms, which look like arrows between dots.
Now, you might object that this is a picture of a _graph_, not a category. And you'd be right! In a category we can _compose_ morphisms, and we also have _identity_ morphisms. So a more detailed mental picture of the same category would look like this:
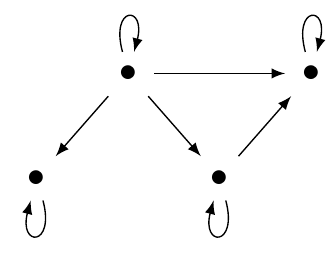 Let's call this category \\(\mathcal{C}\\). Then, a functor \\(F\\) from this category \\(\mathcal{C}\\) to some other category \\(\mathcal{D}\\) would look a bit like this:
Let's call this category \\(\mathcal{C}\\). Then, a functor \\(F\\) from this category \\(\mathcal{C}\\) to some other category \\(\mathcal{D}\\) would look a bit like this:
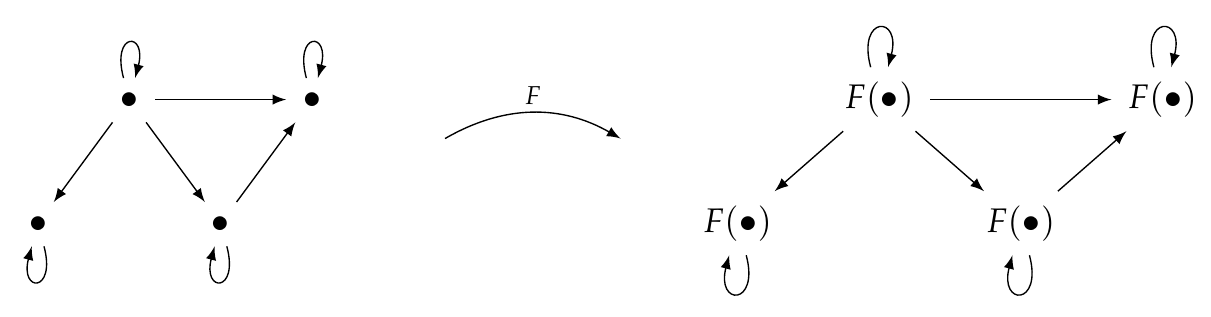 \\(F\\) maps each object of \\(\mathcal{C}\\) to an object in \\(\mathcal{D}\\), and it maps each morphism to a morphism. So, a functor from \\(\mathcal{C}\\) to \\(\mathcal{D}\\) is like _a picture of \\(\,\mathcal{C}\\) drawn on the blackboard of \\(\,\mathcal{D}\\)_.
The category \\(\mathcal{D}\\) may, of course, contain other objects and morphisms that aren't in our picture. To keep things simple I haven't drawn those. Also, two objects or morphisms of \\(\mathcal{C}\\) may get mapped to the same object in \\(\mathcal{D}\\), so the picture of \\(\mathcal{C}\\) in \\(\mathcal{D}\\) could be 'squashed down'. But I haven't drawn that either! You can draw these other possibilities.
Now for the fun part.
Suppose we have two functors from \\(\mathcal{C}\\) to \\(\mathcal{D}\\), say \\(F\\) and \\(G\\). Let me draw them in a stripped-down way:
\\(F\\) maps each object of \\(\mathcal{C}\\) to an object in \\(\mathcal{D}\\), and it maps each morphism to a morphism. So, a functor from \\(\mathcal{C}\\) to \\(\mathcal{D}\\) is like _a picture of \\(\,\mathcal{C}\\) drawn on the blackboard of \\(\,\mathcal{D}\\)_.
The category \\(\mathcal{D}\\) may, of course, contain other objects and morphisms that aren't in our picture. To keep things simple I haven't drawn those. Also, two objects or morphisms of \\(\mathcal{C}\\) may get mapped to the same object in \\(\mathcal{D}\\), so the picture of \\(\mathcal{C}\\) in \\(\mathcal{D}\\) could be 'squashed down'. But I haven't drawn that either! You can draw these other possibilities.
Now for the fun part.
Suppose we have two functors from \\(\mathcal{C}\\) to \\(\mathcal{D}\\), say \\(F\\) and \\(G\\). Let me draw them in a stripped-down way:
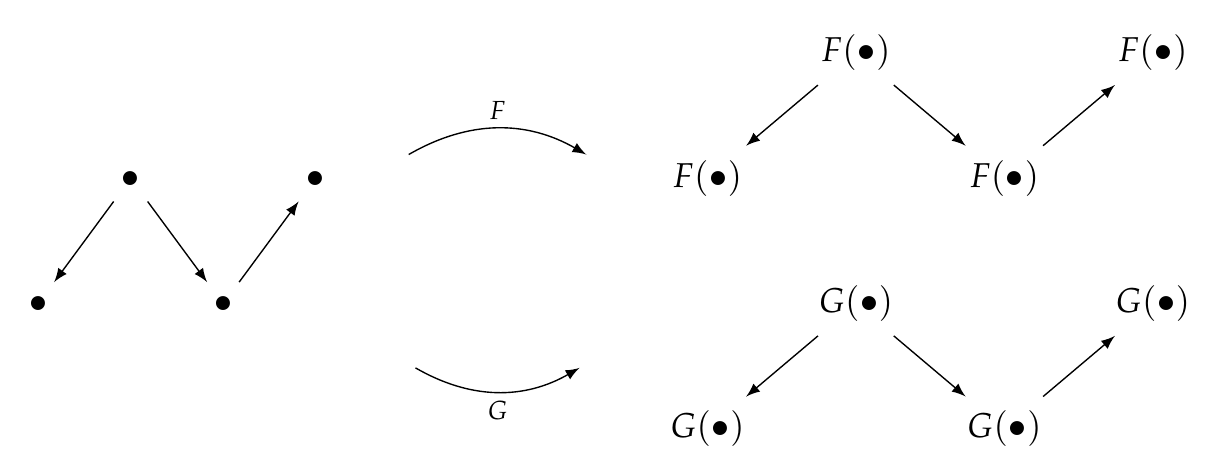 Then we can define a 'natural transformation' from \\(F\\) to \\(G\\), written \\(\alpha : F \Rightarrow G\\). It looks like this:
Then we can define a 'natural transformation' from \\(F\\) to \\(G\\), written \\(\alpha : F \Rightarrow G\\). It looks like this:
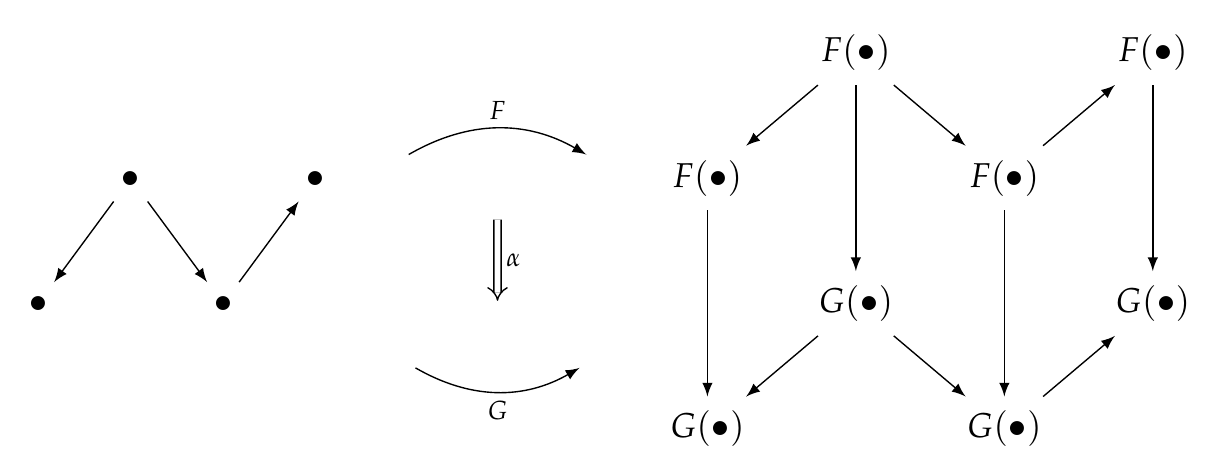 For each object \\(x \in \mathcal{C}\\), the natural transformation gives a morphism from \\(F(x)\\) to \\(G(x)\\). In the picture above I've drawn every objects of \\(\mathcal{C}\\) as a mere dot, but that's a bit sloppy. So let's give all the objects and morphisms names:
For each object \\(x \in \mathcal{C}\\), the natural transformation gives a morphism from \\(F(x)\\) to \\(G(x)\\). In the picture above I've drawn every objects of \\(\mathcal{C}\\) as a mere dot, but that's a bit sloppy. So let's give all the objects and morphisms names:
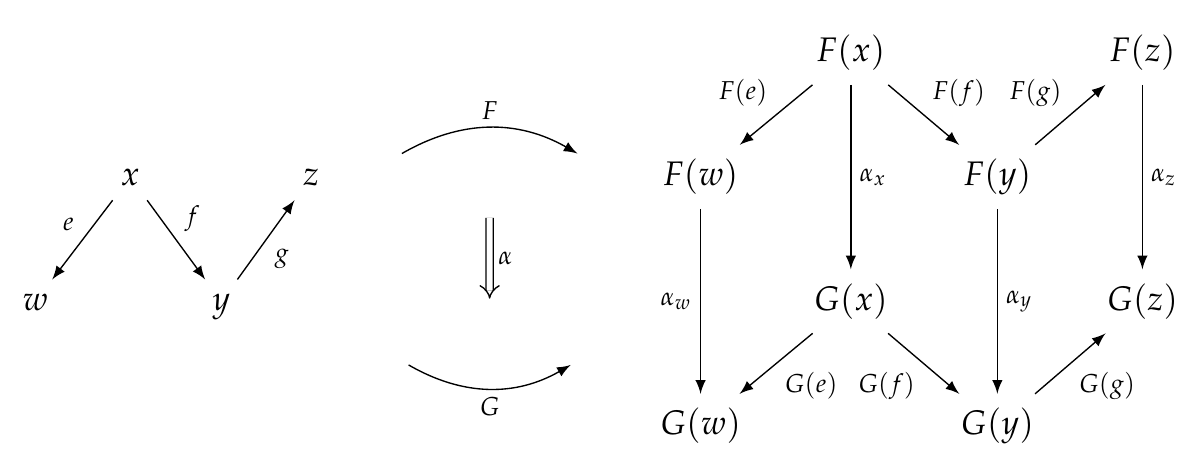 Now we see more clearly that for each object \\(x \in \mathcal{C}\\), the natural transformation \\(\alpha\\) gives a morphism \\(\alpha_x : F(x) \to G(x) \\).
Note that this creates a lot of parallelograms in our picture... or squares, if you draw them like this:
Now we see more clearly that for each object \\(x \in \mathcal{C}\\), the natural transformation \\(\alpha\\) gives a morphism \\(\alpha_x : F(x) \to G(x) \\).
Note that this creates a lot of parallelograms in our picture... or squares, if you draw them like this:
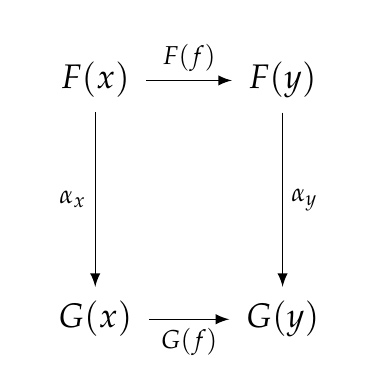 What makes the transformation _natural_ is that all these squares must 'commute': that is, going down and across gives the same morphism as going across and down.
It takes a while to see why this it's so important, but this condition is one of the first really big ideas in category theory. Ways of going between functors that feel 'natural' in an intuitive sense, meaning that they don't involve disorganized random choices, tend to be natural in this technical sense! And it turns out that one can do a lot using this idea.
Indeed, when Eilenberg and Mac Lane came out with their [first paper on category theory](http://www.ams.org/journals/tran/1945-058-00/S0002-9947-1945-0013131-6/S0002-9947-1945-0013131-6.pdf) in 1945, the main topic was natural transformations. Mac Lane later said:
> _I didn't invent categories to study functors; I invented them to study natural transformations._
Okay, now let me give the formal definition:
**Definition.** Given categories \\(\mathcal{C},\mathcal{D}\\) and functors \\(F, G: \mathcal{C} \to \mathcal{D}\\), a **transformation** \\(\alpha : F \to G\\) is a choice of morphism
\[ \alpha_x : F(x) \to G(x) \]
for each objects \\(x \in \mathcal{C}\\). We say the transformation \\(\alpha\\) is **natural** if for each morphism \\(f : x \to y\\) in \\(\mathcal{C}\\), this square commutes:
What makes the transformation _natural_ is that all these squares must 'commute': that is, going down and across gives the same morphism as going across and down.
It takes a while to see why this it's so important, but this condition is one of the first really big ideas in category theory. Ways of going between functors that feel 'natural' in an intuitive sense, meaning that they don't involve disorganized random choices, tend to be natural in this technical sense! And it turns out that one can do a lot using this idea.
Indeed, when Eilenberg and Mac Lane came out with their [first paper on category theory](http://www.ams.org/journals/tran/1945-058-00/S0002-9947-1945-0013131-6/S0002-9947-1945-0013131-6.pdf) in 1945, the main topic was natural transformations. Mac Lane later said:
> _I didn't invent categories to study functors; I invented them to study natural transformations._
Okay, now let me give the formal definition:
**Definition.** Given categories \\(\mathcal{C},\mathcal{D}\\) and functors \\(F, G: \mathcal{C} \to \mathcal{D}\\), a **transformation** \\(\alpha : F \to G\\) is a choice of morphism
\[ \alpha_x : F(x) \to G(x) \]
for each objects \\(x \in \mathcal{C}\\). We say the transformation \\(\alpha\\) is **natural** if for each morphism \\(f : x \to y\\) in \\(\mathcal{C}\\), this square commutes:
 In other words,
\[ G(f) \alpha_x = \alpha_y F(f) .\]
We call a square diagram of this sort a **naturality square.**
Okay, now let's start figuring out what natural transformations are good for!
**Puzzle 126.** Let \\(\mathcal{C}\\) be the free category on this graph:
In other words,
\[ G(f) \alpha_x = \alpha_y F(f) .\]
We call a square diagram of this sort a **naturality square.**
Okay, now let's start figuring out what natural transformations are good for!
**Puzzle 126.** Let \\(\mathcal{C}\\) be the free category on this graph:
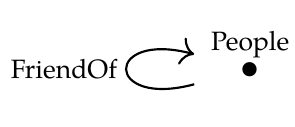 If we treat this as a database schema, a functor \\(F: \mathcal{C} \to \mathbf{Set}\\) is a database built using this schema, and you can draw it as a table, like this:
\\[
\begin{array}{c|c}
\text{People} & \mathrm{FriendOf} \\\\
\hline
Alice & Bob \\\\
Bob & Alice \\\\
Stan & Alice \\\\
Tyler & Stan \\\\
\end{array}
\\]
Suppose \\(G: \mathcal{C} \to \mathbf{Set} \\) is another such database:
\\[
\begin{array}{c|c}
\text{People} & \mathrm{FriendOf} \\\\
\hline
Alice & Bob \\\\
Bob & Alice \\\\
Stan & Alice \\\\
Tyler & Stan \\\\
Mei-Chu & Stan \\\\
\end{array}
\\]
Can you find a natural transformation \\(\alpha : F \Rightarrow G\\) in this example? What is its practical meaning: that is, what could it be used for? What is the significance of naturality in this example?
**Puzzle 127.** Suppose \\(H : \mathcal{C} \to \mathbf{Set} \\) is yet another database built using the same schema, namely
\\[
\begin{array}{c|c}
\text{People} & \mathrm{FriendOf} \\\\
\hline
Alice & Bob \\\\
Bob & Alice \\\\
Tyler & Bob \\\\
\end{array}
\\]
Can you find a natural transformation \\(\beta : F \Rightarrow H\\)? What is its practical meaning? What is the significance of naturality in this example?
**Puzzle 128.** How many natural transformations \\(\gamma: H \Rightarrow H\\) are there? What is their practical meaning?
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_3)**
If we treat this as a database schema, a functor \\(F: \mathcal{C} \to \mathbf{Set}\\) is a database built using this schema, and you can draw it as a table, like this:
\\[
\begin{array}{c|c}
\text{People} & \mathrm{FriendOf} \\\\
\hline
Alice & Bob \\\\
Bob & Alice \\\\
Stan & Alice \\\\
Tyler & Stan \\\\
\end{array}
\\]
Suppose \\(G: \mathcal{C} \to \mathbf{Set} \\) is another such database:
\\[
\begin{array}{c|c}
\text{People} & \mathrm{FriendOf} \\\\
\hline
Alice & Bob \\\\
Bob & Alice \\\\
Stan & Alice \\\\
Tyler & Stan \\\\
Mei-Chu & Stan \\\\
\end{array}
\\]
Can you find a natural transformation \\(\alpha : F \Rightarrow G\\) in this example? What is its practical meaning: that is, what could it be used for? What is the significance of naturality in this example?
**Puzzle 127.** Suppose \\(H : \mathcal{C} \to \mathbf{Set} \\) is yet another database built using the same schema, namely
\\[
\begin{array}{c|c}
\text{People} & \mathrm{FriendOf} \\\\
\hline
Alice & Bob \\\\
Bob & Alice \\\\
Tyler & Bob \\\\
\end{array}
\\]
Can you find a natural transformation \\(\beta : F \Rightarrow H\\)? What is its practical meaning? What is the significance of naturality in this example?
**Puzzle 128.** How many natural transformations \\(\gamma: H \Rightarrow H\\) are there? What is their practical meaning?
**[To read other lectures go here.](http://www.azimuthproject.org/azimuth/show/Applied+Category+Theory#Chapter_3)** 








