_guest post by **[Daniel Cicala](http://math.ucr.edu/~cicala)** and **[Jules Hedges](https://julesh.com/)**_
We continue the [Applied Category Theory Seminar](http://www.appliedcategorytheory.org/school/) with a discussion of Carboni and Walters' paper _[Cartesian Bicategories I](https://www.sciencedirect.com/science/article/pii/0022404987901216)_. The star of this paper is the notion of 'bicategories of relations'. This is an abstraction of relations internal to a category. As such, this paper provides excellent, if technical, examples of internal relations and other internal category theory concepts. In this post, we discuss bicategories of relations while occasionally pausing to enjoy some internal category theory such as relations, adjoints, monads, and the Kleisli construction.
We'd like to thank Brendan Fong and Nina Otter for running such a great seminar. We'd also like to thank Paweł Sobociński and John Baez for helpful discussion.
Shortly after Bénabou introduced bicategories, a program was initiated to study these through profunctor bicategories. Carboni and Walters, however, decided to study bicategories with a more relational flavor. This is not quite as far a departure as one might think. Indeed, relations and profunctors are connected. Let's recall two facts:
* a profunctor from $C$ to $D$ is a functor from $D^{op} \times C \to Set$, and
* a relation between sets $x$ and $y$ can be described with a $\{0,1\}$-valued matrix of size $x \times y$.
Heuristically, profunctors can be thought of as a generalization of relations when considering profunctors as "$\mathbf{Set}$-valued matrix of size $\text{ob} (C) \times \text{ob} (D)$". As such, a line between profunctors and relations appears. In *Cartesian Bicategories I*, authors Carboni and Walters walk this line and continue a study of bicategories from a relational viewpoint.
The primary accomplishment of this paper is to characterize 'bicategories of internal relations' $\mathbf{Rel}(E)$ and of 'ordered objects' $\mathbf{Ord}(E)$ in a regular category $E$. To do this, the authors begin by introducing the notion of Cartesian bicategory, an early example of a *bicategory* with a monoidal product. They then explore **bicategories of relations**, which are Cartesian bicategories whose objects are Frobenius monoids. The name "bicategories of relations" indicates their close relationship with classical relations $\mathbf{Rel}$.
We begin by defining the two most important examples of a bicategory of relations: $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$. Knowing these bicategories will ground us as we wade through the theory of Cartesian bicategories. We finish by characterizing $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$ in terms of the developed theory.
## Internal relations
In set theory, a relation from $x$ to $y$ is a subset of $x \times y$. In category theory, things become more subtle. A relation $r$ from $x$ to $y$ internal to a category $C$ is a 'jointly monic' $C$-span $$x \xleftarrow{r_0} \hat{r} \xrightarrow{r_1} y$$ That is, for any arrows $a , b \colon u \to \hat{r}$ such that $r_0 a = r_0 b$ and $r_1 a = r_1 b$ hold, then $a = b$. In a category with products, this definition simplifies substantially; it is merely a monic arrow $r \colon \hat{r} \to x \times y$.
Given a span $x \xleftarrow{c} w \xrightarrow{d} y$ and the relation $r \coloneqq \langle r_0 , r_1 \rangle $ from above, we say that $c$ is $r$-related to $d$ if there is an $w \to \hat{r}$ so that
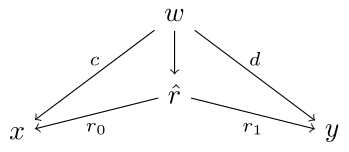 commutes. We will write $ r \colon c \nrightarrow d$ when $c$ is $r$-related to $d$.
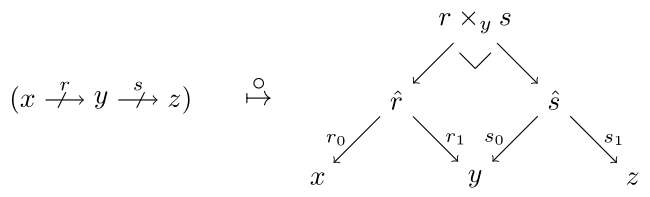
While we can talk about relations internal to $any$ category, we cannot generally assemble them into another category. However, if we start with a [regular category](https://ncatlab.org/nlab/show/regular+category) $E$, then there is a bicategory $\mathbf{Rel}(E)$ of relations internal to $E$. The objects are those of $E$. The arrows are the relations internal to $E$ with composition given by pullback:
commutes. We will write $ r \colon c \nrightarrow d$ when $c$ is $r$-related to $d$.
While we can talk about relations internal to $any$ category, we cannot generally assemble them into another category. However, if we start with a [regular category](https://ncatlab.org/nlab/show/regular+category) $E$, then there is a bicategory $\mathbf{Rel}(E)$ of relations internal to $E$. The objects are those of $E$. The arrows are the relations internal to $E$ with composition given by pullback:
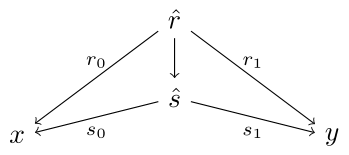
 Additionally, we have a unique 2-cell, written $r \leq s$, whenever $ s \colon r_0 \nrightarrow r_1 $. Diagrammatically, $r \leq s$ if there exists a commuting diagram
Additionally, we have a unique 2-cell, written $r \leq s$, whenever $ s \colon r_0 \nrightarrow r_1 $. Diagrammatically, $r \leq s$ if there exists a commuting diagram
 ### Internal ordered objects
We are quite used to the idea of having an order on a set. But what about an order on a category? This is captured by $\mathbf{Ord}(E),$ the bicategory of ordered objects and ideals in a regular category $E$.
The objects of $\mathbf{Ord}(E)$ are ordered objects in $E$. An **ordered object** is a pair $(x,r)$ consisting of an $E$-object $x$ and a reflexive and transitive relation $r : x \to x$ internal to $E$.
*(Puzzle: $ r $ is a monic of type $ r \colon \hat{r} \to x \times x$. Both reflexivity and transitivity can be defined using morphisms. What are the domains and codomains? What properties should be satisfied?)*
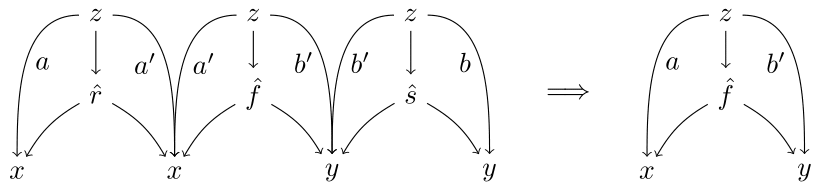
The arrows of $\mathbf{Ord}(E)$ are a sort of 'order preserving relation' called an ideal. Precisely, an **ideal** $f \colon (x,r) \to (y,s)$ between ordered objects is a relation $f \colon x \nrightarrow y$ such that given
* morphisms $ a , a' , b , b' $ with a common domain $ z $, and
* relations $ r \colon a \nrightarrow a'$, $ f \colon a' \nrightarrow b'$, and $ s \colon b' \nrightarrow b $
then $ f \colon a \nrightarrow b$.
### Internal ordered objects
We are quite used to the idea of having an order on a set. But what about an order on a category? This is captured by $\mathbf{Ord}(E),$ the bicategory of ordered objects and ideals in a regular category $E$.
The objects of $\mathbf{Ord}(E)$ are ordered objects in $E$. An **ordered object** is a pair $(x,r)$ consisting of an $E$-object $x$ and a reflexive and transitive relation $r : x \to x$ internal to $E$.
*(Puzzle: $ r $ is a monic of type $ r \colon \hat{r} \to x \times x$. Both reflexivity and transitivity can be defined using morphisms. What are the domains and codomains? What properties should be satisfied?)*
The arrows of $\mathbf{Ord}(E)$ are a sort of 'order preserving relation' called an ideal. Precisely, an **ideal** $f \colon (x,r) \to (y,s)$ between ordered objects is a relation $f \colon x \nrightarrow y$ such that given
* morphisms $ a , a' , b , b' $ with a common domain $ z $, and
* relations $ r \colon a \nrightarrow a'$, $ f \colon a' \nrightarrow b'$, and $ s \colon b' \nrightarrow b $
then $ f \colon a \nrightarrow b$.
 In $ \mathbf{Set} $, an ordered object is a preordered set and an ideal $ f \colon (x,r) \to (y,s) $ is a directed subset of $x \times y $ with the property that if it contains $ s $ and $ s' \leq s $, then it contains $ s' $.
There is at most a single 2-cell between parallel arrows in $\mathbf{Ord}(E)$. Given $f , g \colon (x,r) \to (y,s)$, write $f \leq g$ whenever $ g \colon f_0 \nrightarrow f_1 $.
## Cartesian Bicategories
Now that we know what bicategories we have the pleasure of working with, we can move forward with the theoretical aspects. As we work through the upcoming definitions, it is helpful to recall our motivating examples $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$.
As mentioned above, in the early days of bicategory theory, mathematicians would study bicategories as $V$-enriched profunctor bicategories for some suitable $V$. A shrewd observation was made that when $V$ is Cartesian, a $V$-profunctor bicategory has several important commonalities with $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$. Namely, there is the existence of a Cartesian product $\otimes$, plus for each object $x$, a diagonal arrow $\Delta \colon x \to x \otimes x$ and terminal object $\epsilon \colon x \to I$. With this insight, Carboni and Walters decided to take this structute as primitive.
To simplify coherence, we only look at locally posetal bicategories (i.e. $\mathbf{Pos}$-enriched categories). This renders 2-dimensional coherences redundant as all parallel 2-cells manifestly commute. This assumption also endows each hom-poset with 2-cells $\leq$ and, as we will see, local meets $\wedge$. For the remainder of this article, all bicategories will be locally posetal unless otherwise stated.
**Definition.** A locally posetal bicategory $B$ is **Cartesian** when equipped with
* a symmetric tensor product $B \otimes B \to B$,
* a cocommutative comonoid structure, $\Delta_x \colon x \to x \otimes x$, and $\epsilon_x \colon x \to I$, on every $B$-object $x$
such that
* every 1-arrow $r \colon x \to y$ is a lax comonoid homomorphism, i.e.
$$
\Delta_y r \leq ( r \otimes r ) \Delta_x
\quad \text{and} \quad
\epsilon_y r \leq \epsilon_x
$$
* for all objects $x$, both $\Delta_x$ and $\epsilon_x$ have right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$.
Moreover, $(\Delta_x , \epsilon_x)$ is the *only* cocommutative comonoid structure on $x$ admitting right adjoints.
*(Question: This definition contains a slight ambiguity in the authors use of the term "moreover". Is the uniqueness property of the cocommutative comonoid structure an additional axiom or does it follow from the other axioms?)*
If you're not accustomed to thinking about adjoints internal to a general bicategory, place yourself for a moment in $\mathbf{Cat}$. Recall that adjoint functors are merely a pair of *arrows* (adjoint functors) together with a pair of *2-cells* (unit and counit) obeying certain equations. But this sort of data can exist in *any* bicategory, not just $\mathbf{Cat}$. It is worth spending a minute to feel comfortable with this concept because, in what follows, adjoints play an important role.
Observe that the right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$ turn $x$ into a commutative monoid object, hence a bimonoid. The (co)commutative (co)monoid structure on an object $x$ extend to a tensor product on $x \otimes x$ as seen in this string diagram:
In $ \mathbf{Set} $, an ordered object is a preordered set and an ideal $ f \colon (x,r) \to (y,s) $ is a directed subset of $x \times y $ with the property that if it contains $ s $ and $ s' \leq s $, then it contains $ s' $.
There is at most a single 2-cell between parallel arrows in $\mathbf{Ord}(E)$. Given $f , g \colon (x,r) \to (y,s)$, write $f \leq g$ whenever $ g \colon f_0 \nrightarrow f_1 $.
## Cartesian Bicategories
Now that we know what bicategories we have the pleasure of working with, we can move forward with the theoretical aspects. As we work through the upcoming definitions, it is helpful to recall our motivating examples $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$.
As mentioned above, in the early days of bicategory theory, mathematicians would study bicategories as $V$-enriched profunctor bicategories for some suitable $V$. A shrewd observation was made that when $V$ is Cartesian, a $V$-profunctor bicategory has several important commonalities with $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$. Namely, there is the existence of a Cartesian product $\otimes$, plus for each object $x$, a diagonal arrow $\Delta \colon x \to x \otimes x$ and terminal object $\epsilon \colon x \to I$. With this insight, Carboni and Walters decided to take this structute as primitive.
To simplify coherence, we only look at locally posetal bicategories (i.e. $\mathbf{Pos}$-enriched categories). This renders 2-dimensional coherences redundant as all parallel 2-cells manifestly commute. This assumption also endows each hom-poset with 2-cells $\leq$ and, as we will see, local meets $\wedge$. For the remainder of this article, all bicategories will be locally posetal unless otherwise stated.
**Definition.** A locally posetal bicategory $B$ is **Cartesian** when equipped with
* a symmetric tensor product $B \otimes B \to B$,
* a cocommutative comonoid structure, $\Delta_x \colon x \to x \otimes x$, and $\epsilon_x \colon x \to I$, on every $B$-object $x$
such that
* every 1-arrow $r \colon x \to y$ is a lax comonoid homomorphism, i.e.
$$
\Delta_y r \leq ( r \otimes r ) \Delta_x
\quad \text{and} \quad
\epsilon_y r \leq \epsilon_x
$$
* for all objects $x$, both $\Delta_x$ and $\epsilon_x$ have right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$.
Moreover, $(\Delta_x , \epsilon_x)$ is the *only* cocommutative comonoid structure on $x$ admitting right adjoints.
*(Question: This definition contains a slight ambiguity in the authors use of the term "moreover". Is the uniqueness property of the cocommutative comonoid structure an additional axiom or does it follow from the other axioms?)*
If you're not accustomed to thinking about adjoints internal to a general bicategory, place yourself for a moment in $\mathbf{Cat}$. Recall that adjoint functors are merely a pair of *arrows* (adjoint functors) together with a pair of *2-cells* (unit and counit) obeying certain equations. But this sort of data can exist in *any* bicategory, not just $\mathbf{Cat}$. It is worth spending a minute to feel comfortable with this concept because, in what follows, adjoints play an important role.
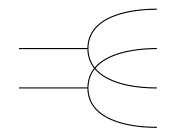
Observe that the right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$ turn $x$ into a commutative monoid object, hence a bimonoid. The (co)commutative (co)monoid structure on an object $x$ extend to a tensor product on $x \otimes x$ as seen in this string diagram:
 Ultimately, we want to think of arrows in a Cartesian bicategory as generalized relations. What other considerations are required to do this? To answer this, it is helpful to first think about what a generalized function should be.
For the moment, let's use our $\mathbf{Set}$ based intuition. For a relation to be a function, we ask that every element of the domain is related to an element of the codomain (entireness) and that the relationship is unique (determinism). How do we encode these requirements into this new, general situation? Again, let's use intuition from relations in $\mathbf{Set}$. Let $r \nrightarrow x \times y$ be a relation and $r^\circ \nrightarrow y \times x$ be the relation defined by $ r^{\circ} \colon y \nrightarrow x $ whenever $r \colon x \nrightarrow y$. To say that $r$ is entire is equivalent to saying that the composite relation $r^\circ r$ contains the identity relation on $x$ *(puzzle)*. To say that $r$ is deterministic is to say that the composite relation $rr^\circ$ is contained by the identity *(another puzzle)*. These two containments are concisely expressed by writing $1 \leq r^\circ r$ and $r r^\circ \leq 1$. Hence $r$ and $r^\circ$ form an adjoint pair! This leads us to the following definition.
**Definition.** An arrow of a Cartesian bicategory is a **map** when it has a right adjoint. Maps are closed under identity and composition. Hence, for any Cartesian bicategory $B$, there is the full subbicategory $\mathbf{Map}(B)$ whose arrows are the maps in $B$.
*(Puzzle: There is an equivalences of categories $E \simeq \mathbf{Map}(\mathbf{Rel}(E))$ for a regular category $E$. What does this say for $E := \mathbf{Set}$?)*
We can now state what appears as Theorem 1.6 of the paper. Recall that $(-)^\ast$ refers to the right adjoint.
**Theorem.** Let $B$ be a locally posetal bicategory. If $B$ is Cartesian, then
* $\mathbf{Map}(B)$ has finite biproducts $\otimes$,
* the hom-posets have finite meets $\wedge$ (i.e. categorical products) and the identity arrow in $B(I,I)$ is maximal (i.e. a terminal object), and
* biproducts and the biterminal object in $\mathbf{Map}(B)$ may be chosen so that $r \otimes s = (p^\ast r p) \wedge (p s p^\ast)$,where $p$ denotes the appropriate projection.
Conversely, if the first two properties are satisfied and the third defines a tensor product, then $B$ is Cartesian.
This theorem gives a nice characterisation of Cartesian bicategories. The first two axioms are straightforward enough, but what is the significance of the above tensor product equation?
It's actually quite painless when you break it down. Note, every biproduct $\otimes$ comes with projections $p$ and inclusions $p^\ast$. Now, let $r \colon w \to y$ and $s \colon x \to z$ which gives $r \otimes s \colon w \otimes x \to y \otimes z$. One canonical arrow of type $w \otimes x \to y \otimes z$ is $p^\ast r p$ which first projects to $w$, arrives at $y$ via $r$, which then includes into $y \otimes w$. The other arrow is similar, except we first project to $x$. The above theorem says that by combining these two arrows with a meet $\wedge$, the only available operation, we get our tensor product.
## Characterizing bicatgories of internal relations
The next stage is to add to Cartesian bicategories the property that each object is a Frobenius monoid. In this section we will study such bicategories and see that Cartesian plus Frobenius provides a reasonable axiomatization of relations.
Recall that an object with monoid and comonoid structures is called a **Frobenius monoid** if the equation
Ultimately, we want to think of arrows in a Cartesian bicategory as generalized relations. What other considerations are required to do this? To answer this, it is helpful to first think about what a generalized function should be.
For the moment, let's use our $\mathbf{Set}$ based intuition. For a relation to be a function, we ask that every element of the domain is related to an element of the codomain (entireness) and that the relationship is unique (determinism). How do we encode these requirements into this new, general situation? Again, let's use intuition from relations in $\mathbf{Set}$. Let $r \nrightarrow x \times y$ be a relation and $r^\circ \nrightarrow y \times x$ be the relation defined by $ r^{\circ} \colon y \nrightarrow x $ whenever $r \colon x \nrightarrow y$. To say that $r$ is entire is equivalent to saying that the composite relation $r^\circ r$ contains the identity relation on $x$ *(puzzle)*. To say that $r$ is deterministic is to say that the composite relation $rr^\circ$ is contained by the identity *(another puzzle)*. These two containments are concisely expressed by writing $1 \leq r^\circ r$ and $r r^\circ \leq 1$. Hence $r$ and $r^\circ$ form an adjoint pair! This leads us to the following definition.
**Definition.** An arrow of a Cartesian bicategory is a **map** when it has a right adjoint. Maps are closed under identity and composition. Hence, for any Cartesian bicategory $B$, there is the full subbicategory $\mathbf{Map}(B)$ whose arrows are the maps in $B$.
*(Puzzle: There is an equivalences of categories $E \simeq \mathbf{Map}(\mathbf{Rel}(E))$ for a regular category $E$. What does this say for $E := \mathbf{Set}$?)*
We can now state what appears as Theorem 1.6 of the paper. Recall that $(-)^\ast$ refers to the right adjoint.
**Theorem.** Let $B$ be a locally posetal bicategory. If $B$ is Cartesian, then
* $\mathbf{Map}(B)$ has finite biproducts $\otimes$,
* the hom-posets have finite meets $\wedge$ (i.e. categorical products) and the identity arrow in $B(I,I)$ is maximal (i.e. a terminal object), and
* biproducts and the biterminal object in $\mathbf{Map}(B)$ may be chosen so that $r \otimes s = (p^\ast r p) \wedge (p s p^\ast)$,where $p$ denotes the appropriate projection.
Conversely, if the first two properties are satisfied and the third defines a tensor product, then $B$ is Cartesian.
This theorem gives a nice characterisation of Cartesian bicategories. The first two axioms are straightforward enough, but what is the significance of the above tensor product equation?
It's actually quite painless when you break it down. Note, every biproduct $\otimes$ comes with projections $p$ and inclusions $p^\ast$. Now, let $r \colon w \to y$ and $s \colon x \to z$ which gives $r \otimes s \colon w \otimes x \to y \otimes z$. One canonical arrow of type $w \otimes x \to y \otimes z$ is $p^\ast r p$ which first projects to $w$, arrives at $y$ via $r$, which then includes into $y \otimes w$. The other arrow is similar, except we first project to $x$. The above theorem says that by combining these two arrows with a meet $\wedge$, the only available operation, we get our tensor product.
## Characterizing bicatgories of internal relations
The next stage is to add to Cartesian bicategories the property that each object is a Frobenius monoid. In this section we will study such bicategories and see that Cartesian plus Frobenius provides a reasonable axiomatization of relations.
Recall that an object with monoid and comonoid structures is called a **Frobenius monoid** if the equation
 holds. If you're not familiar with this equation, it has an interesting history as [outlined by Walters](http://rfcwalters.blogspot.com/2006/02/history-of-equation-1-tensor.html). Now, if every object in a Cartesian bicategory is a Frobenius monoid, we call it a **bicategory of relations**. This term is a bit overworked as it commonly refers to $\mathbf{Rel}(E)$. Therefore, we will be careful to call the latter a "bicategory of internal relations".
Why are bicatgories of relations better than simply Cartesian bicategories? For one, they admit a compact closed structure! This appears as Theorem 2.4 in the paper.
**Theorem.** A bicategory of relations has a compact closed structure. Objects are self-dual via the unit
$$
\Delta \epsilon^\ast_x \colon I \to x \otimes x
$$
and counit
$$
\epsilon \Delta^\ast_x \colon x \otimes x \to I. $$
Moreover, the dual $r^\circ$ of any arrow $r \colon x \to y$ satisfies
$$
(r \otimes id) \Delta \leq (1 \otimes r^\circ) \Delta r
$$
and
$$
\Delta^\ast (r \otimes id) \leq r \Delta^\ast (1 \otimes r^\circ).
$$
Or if you prefer string diagrams, the above inequalities are respectively
holds. If you're not familiar with this equation, it has an interesting history as [outlined by Walters](http://rfcwalters.blogspot.com/2006/02/history-of-equation-1-tensor.html). Now, if every object in a Cartesian bicategory is a Frobenius monoid, we call it a **bicategory of relations**. This term is a bit overworked as it commonly refers to $\mathbf{Rel}(E)$. Therefore, we will be careful to call the latter a "bicategory of internal relations".
Why are bicatgories of relations better than simply Cartesian bicategories? For one, they admit a compact closed structure! This appears as Theorem 2.4 in the paper.
**Theorem.** A bicategory of relations has a compact closed structure. Objects are self-dual via the unit
$$
\Delta \epsilon^\ast_x \colon I \to x \otimes x
$$
and counit
$$
\epsilon \Delta^\ast_x \colon x \otimes x \to I. $$
Moreover, the dual $r^\circ$ of any arrow $r \colon x \to y$ satisfies
$$
(r \otimes id) \Delta \leq (1 \otimes r^\circ) \Delta r
$$
and
$$
\Delta^\ast (r \otimes id) \leq r \Delta^\ast (1 \otimes r^\circ).
$$
Or if you prefer string diagrams, the above inequalities are respectively
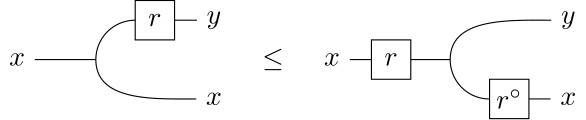 and
and
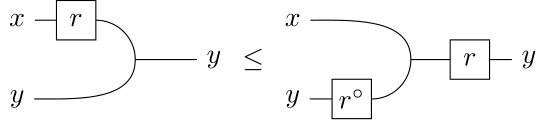 Because a bicategory of relations is Cartesian, maps are still present. In fact, they have a very nice characterization here.
**Lemma.** In a bicategory of relations, an arrow $r$ is a map iff it is a (strict) comonoid homomorphism iff $r \dashv r^\circ$.
As one would hope, the adjoint of a map corresponds with the involution coming from the compact closed structure. The following corollary provides further evidence that maps are well-behaved.
**Corollary.** In a bicategory of relations:
* $f$ is a map implies $f^\circ = f^\ast$. In particular, multiplication is adjoint to comultiplication and the unit is adjoint to the counit.
* for maps $f$ and $g$, if $f \leq g$ then $f=g$.
But maps don't merely behave in a nice way. They also contain a lot of the information about a Cartesian bicategory and, when working with bicategories of relations, the local information is quite fruitful too. This is made precise in the following corollary.
**Corollary.** Let $F \colon B \to D$ be a pseudofunctor between bicategories of relations. The following are equivalent:
* $F$ strictly preserves the Frobenius structure.
* The restriction $F \colon \mathbf{Map}(B) \to \mathbf{Map}(D)$ strictly preserves the comonoid structure.
* $F$ preserves local meets and $I$.
## Characterizing bicategories of internal relations
The entire point of the theory developed above is to be able to prove things about certain classes of bicategories. In this section, we provide a characterization theorem for bicategories of internal relations. Freyd had already given this characterization using [allegories](https://ncatlab.org/nlab/show/allegory#maps_tabulations_and_units). However, he relied on a proof by contradiction whereas using bicategories of relations allows for a constructive proof.
A bicategory of relations is meant to generalize bicategories of internal relations. Given a bicategory of relations, we'd like to know when an arrow is "like an internal relation".
**Definition.** An arrow $r \colon x \to y$ is a **tabulation** if there exists maps $f \colon z \to x$ and $g \colon z \to y$ such that $r = g f^\ast$ and $f^\ast f \wedge g^\ast g = 1_z$.
Because a bicategory of relations is Cartesian, maps are still present. In fact, they have a very nice characterization here.
**Lemma.** In a bicategory of relations, an arrow $r$ is a map iff it is a (strict) comonoid homomorphism iff $r \dashv r^\circ$.
As one would hope, the adjoint of a map corresponds with the involution coming from the compact closed structure. The following corollary provides further evidence that maps are well-behaved.
**Corollary.** In a bicategory of relations:
* $f$ is a map implies $f^\circ = f^\ast$. In particular, multiplication is adjoint to comultiplication and the unit is adjoint to the counit.
* for maps $f$ and $g$, if $f \leq g$ then $f=g$.
But maps don't merely behave in a nice way. They also contain a lot of the information about a Cartesian bicategory and, when working with bicategories of relations, the local information is quite fruitful too. This is made precise in the following corollary.
**Corollary.** Let $F \colon B \to D$ be a pseudofunctor between bicategories of relations. The following are equivalent:
* $F$ strictly preserves the Frobenius structure.
* The restriction $F \colon \mathbf{Map}(B) \to \mathbf{Map}(D)$ strictly preserves the comonoid structure.
* $F$ preserves local meets and $I$.
## Characterizing bicategories of internal relations
The entire point of the theory developed above is to be able to prove things about certain classes of bicategories. In this section, we provide a characterization theorem for bicategories of internal relations. Freyd had already given this characterization using [allegories](https://ncatlab.org/nlab/show/allegory#maps_tabulations_and_units). However, he relied on a proof by contradiction whereas using bicategories of relations allows for a constructive proof.
A bicategory of relations is meant to generalize bicategories of internal relations. Given a bicategory of relations, we'd like to know when an arrow is "like an internal relation".
**Definition.** An arrow $r \colon x \to y$ is a **tabulation** if there exists maps $f \colon z \to x$ and $g \colon z \to y$ such that $r = g f^\ast$ and $f^\ast f \wedge g^\ast g = 1_z$.
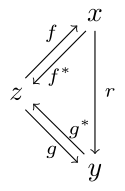 This definition seems bizarre on its face, but it really is analogous to the jointly monic span-definition of an internal relation. That $r = g f^\ast$ is saying that $r$ is like a span $x \xleftarrow{f} z \xrightarrow{g} y$. The equation $f^\ast f \wedge g^\ast g = 1_z$ implies that this span is jointly monic *(puzzle)*.
A bicategory of relations is called **functionally complete** if every arrow $r \colon x \to I$ has a tabulation $i \colon x_r \to x$ and $t \colon x_r \to I$. One can show that the existence of these tabulations together with compact closedness is sufficient to obtain a unique (up to isomorphism) tabulation for every arrow. We now provide the characterization, presented as Theorem 3.5.
**Theorem.** Let $B$ be a functionally complete bicategory of relations. Then:
* $\mathbf{Map}(B)$ is a regular category (all 2-arrows are trivial by an above corollary)
* There is a biequivalence of bicategories $\mathbf{Rel}(\mathbf{Map}(B)) \simeq B$ obtained by sending the relation $\langle f,g \rangle$ of $\mathbf{Rel}(\mathbf{Map}(B))$ to the arrow $g f^\circ$ of $B$.
So all functionally complete bicategories of relations *are* bicategories of internal relations. An interesting quesion is whether any regular category can be realized as $\mathbf{Map}(B)$ for some functionally complete bicategory of relations. Perhaps a knowledgeable passerby will gift us with an answer in the comments!
From this theorem, we can classify some important types of categories. For instance, bicategories of relations internal to a Heyting category are exactly the functionally complete bicategory of relations having all right Kan extensions. Bicategories of relations internal to an elementary topos are exactly the functionally complete bicategories of relations $B$ such that $B(x,-)$ is representable in $\mathbf{Map}(B)$ for all objects $x$.
## Characterizing ordered object bicategories
The goal of this section is to characterize the bicategory $\mathbf{Ord}(E)$ of ordered objects and ideals. We already introduced $\mathbf{Ord}(E)$ earlier, but that definition isn't quite abstract enough for our purposes. An equivalent way of defining an ordered object in $E$ is as an $E$-object $x$ together with a relation $r$ on $x$ such that $1 \leq r$ and $r r \leq r$. Does this data look familiar? An ordered object in $E$ is simply a monad in $\mathbf{Rel}(E)$!
*(Puzzle: What is a monad in a general bicategory? Hint: how are adjoints defined in a general bicategory?)*
Quite a bit is known about monads, and we can now apply that knowledge to our study of $\mathbf{Ord}(E)$.
Recall that any monad in $\mathbf{Cat}$ gives rise to a category of adjunctions. The initial object of this category is the Kleisli category. Since the Kleisli category can be defined using a universal property, we can define a Kleisli object in any bicategory. In general, a Kleisli object for a monad $t \colon x \to x$ need not exist but when it does, it is defined as an arrow $k : x \to x_t$ plus a 2-arrow $\theta \colon k t \to k$ such that, given any arrow $f \colon x \to y$ and 2-arrow $\alpha \colon f t \to f$, there exists a unique arrow $h \colon x_t \to y$ such that $h k = f$. The pasting diagrams involved also commute:
This definition seems bizarre on its face, but it really is analogous to the jointly monic span-definition of an internal relation. That $r = g f^\ast$ is saying that $r$ is like a span $x \xleftarrow{f} z \xrightarrow{g} y$. The equation $f^\ast f \wedge g^\ast g = 1_z$ implies that this span is jointly monic *(puzzle)*.
A bicategory of relations is called **functionally complete** if every arrow $r \colon x \to I$ has a tabulation $i \colon x_r \to x$ and $t \colon x_r \to I$. One can show that the existence of these tabulations together with compact closedness is sufficient to obtain a unique (up to isomorphism) tabulation for every arrow. We now provide the characterization, presented as Theorem 3.5.
**Theorem.** Let $B$ be a functionally complete bicategory of relations. Then:
* $\mathbf{Map}(B)$ is a regular category (all 2-arrows are trivial by an above corollary)
* There is a biequivalence of bicategories $\mathbf{Rel}(\mathbf{Map}(B)) \simeq B$ obtained by sending the relation $\langle f,g \rangle$ of $\mathbf{Rel}(\mathbf{Map}(B))$ to the arrow $g f^\circ$ of $B$.
So all functionally complete bicategories of relations *are* bicategories of internal relations. An interesting quesion is whether any regular category can be realized as $\mathbf{Map}(B)$ for some functionally complete bicategory of relations. Perhaps a knowledgeable passerby will gift us with an answer in the comments!
From this theorem, we can classify some important types of categories. For instance, bicategories of relations internal to a Heyting category are exactly the functionally complete bicategory of relations having all right Kan extensions. Bicategories of relations internal to an elementary topos are exactly the functionally complete bicategories of relations $B$ such that $B(x,-)$ is representable in $\mathbf{Map}(B)$ for all objects $x$.
## Characterizing ordered object bicategories
The goal of this section is to characterize the bicategory $\mathbf{Ord}(E)$ of ordered objects and ideals. We already introduced $\mathbf{Ord}(E)$ earlier, but that definition isn't quite abstract enough for our purposes. An equivalent way of defining an ordered object in $E$ is as an $E$-object $x$ together with a relation $r$ on $x$ such that $1 \leq r$ and $r r \leq r$. Does this data look familiar? An ordered object in $E$ is simply a monad in $\mathbf{Rel}(E)$!
*(Puzzle: What is a monad in a general bicategory? Hint: how are adjoints defined in a general bicategory?)*
Quite a bit is known about monads, and we can now apply that knowledge to our study of $\mathbf{Ord}(E)$.
Recall that any monad in $\mathbf{Cat}$ gives rise to a category of adjunctions. The initial object of this category is the Kleisli category. Since the Kleisli category can be defined using a universal property, we can define a Kleisli object in any bicategory. In general, a Kleisli object for a monad $t \colon x \to x$ need not exist but when it does, it is defined as an arrow $k : x \to x_t$ plus a 2-arrow $\theta \colon k t \to k$ such that, given any arrow $f \colon x \to y$ and 2-arrow $\alpha \colon f t \to f$, there exists a unique arrow $h \colon x_t \to y$ such that $h k = f$. The pasting diagrams involved also commute:
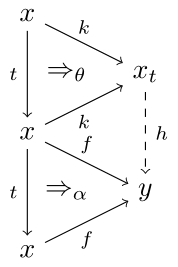 As in the case of working inside $\mathbf{Cat}$, we would expect for $k$ to be on the left of an adjoint pair, and indeed it is. We get a right adjoint $k^\ast$ such that the composite $k^\ast k$ is our original monad $t$. The benefit of working in the locally posetal case is we also have that $k k^\ast = 1$. This realizes $t$ as an idempotent:
$$ t t
= k^\ast k k^\ast k
= k^\ast k
= t. $$
It follows that the Kleisli object construction is exactly an idempotent splitting of $t$! This means we can start with an exact category $E$ and construct $\mathbf{Ord}(E)$ by splitting the idempotents of $\mathbf{Rel}(E)$. With this in mind, we move on to the characterization, presented as Theorem 4.6.
**Theorem.** A bicategory $B$ is biequivalent to a bicategory $\mathbf{Ord}(E)$ if and only if
* $B$ is Cartesian,
* every monad in $B$ has a Kleisli object,
* for each object $x$, there is a monad on $x$ and a Frobenius monoid $x_0$ that is isomorphic to the monad's Kleisli object,
* given a Frobenius monoid x and $f \colon x \to x$ with $f \leq 1$, $f$ splits.
## Final words
The authors go on to look closer at bicategories of relations inside Grothendieck topoi and abelian categories. Both of these are regular categories, and so fit into the picture we've just painted. However, each have additional properties and structure that compels further study.
Much of what we have done can be done in greater generality. For instance, we can drop the local posetal requirement. However, this would greatly complicate matters by requiring non-trivial coherence conditions.
As in the case of working inside $\mathbf{Cat}$, we would expect for $k$ to be on the left of an adjoint pair, and indeed it is. We get a right adjoint $k^\ast$ such that the composite $k^\ast k$ is our original monad $t$. The benefit of working in the locally posetal case is we also have that $k k^\ast = 1$. This realizes $t$ as an idempotent:
$$ t t
= k^\ast k k^\ast k
= k^\ast k
= t. $$
It follows that the Kleisli object construction is exactly an idempotent splitting of $t$! This means we can start with an exact category $E$ and construct $\mathbf{Ord}(E)$ by splitting the idempotents of $\mathbf{Rel}(E)$. With this in mind, we move on to the characterization, presented as Theorem 4.6.
**Theorem.** A bicategory $B$ is biequivalent to a bicategory $\mathbf{Ord}(E)$ if and only if
* $B$ is Cartesian,
* every monad in $B$ has a Kleisli object,
* for each object $x$, there is a monad on $x$ and a Frobenius monoid $x_0$ that is isomorphic to the monad's Kleisli object,
* given a Frobenius monoid x and $f \colon x \to x$ with $f \leq 1$, $f$ splits.
## Final words
The authors go on to look closer at bicategories of relations inside Grothendieck topoi and abelian categories. Both of these are regular categories, and so fit into the picture we've just painted. However, each have additional properties and structure that compels further study.
Much of what we have done can be done in greater generality. For instance, we can drop the local posetal requirement. However, this would greatly complicate matters by requiring non-trivial coherence conditions. commutes. We will write $ r \colon c \nrightarrow d$ when $c$ is $r$-related to $d$.
While we can talk about relations internal to $any$ category, we cannot generally assemble them into another category. However, if we start with a [regular category](https://ncatlab.org/nlab/show/regular+category) $E$, then there is a bicategory $\mathbf{Rel}(E)$ of relations internal to $E$. The objects are those of $E$. The arrows are the relations internal to $E$ with composition given by pullback:
commutes. We will write $ r \colon c \nrightarrow d$ when $c$ is $r$-related to $d$.
While we can talk about relations internal to $any$ category, we cannot generally assemble them into another category. However, if we start with a [regular category](https://ncatlab.org/nlab/show/regular+category) $E$, then there is a bicategory $\mathbf{Rel}(E)$ of relations internal to $E$. The objects are those of $E$. The arrows are the relations internal to $E$ with composition given by pullback:
 Additionally, we have a unique 2-cell, written $r \leq s$, whenever $ s \colon r_0 \nrightarrow r_1 $. Diagrammatically, $r \leq s$ if there exists a commuting diagram
Additionally, we have a unique 2-cell, written $r \leq s$, whenever $ s \colon r_0 \nrightarrow r_1 $. Diagrammatically, $r \leq s$ if there exists a commuting diagram
 ### Internal ordered objects
We are quite used to the idea of having an order on a set. But what about an order on a category? This is captured by $\mathbf{Ord}(E),$ the bicategory of ordered objects and ideals in a regular category $E$.
The objects of $\mathbf{Ord}(E)$ are ordered objects in $E$. An **ordered object** is a pair $(x,r)$ consisting of an $E$-object $x$ and a reflexive and transitive relation $r : x \to x$ internal to $E$.
*(Puzzle: $ r $ is a monic of type $ r \colon \hat{r} \to x \times x$. Both reflexivity and transitivity can be defined using morphisms. What are the domains and codomains? What properties should be satisfied?)*
The arrows of $\mathbf{Ord}(E)$ are a sort of 'order preserving relation' called an ideal. Precisely, an **ideal** $f \colon (x,r) \to (y,s)$ between ordered objects is a relation $f \colon x \nrightarrow y$ such that given
* morphisms $ a , a' , b , b' $ with a common domain $ z $, and
* relations $ r \colon a \nrightarrow a'$, $ f \colon a' \nrightarrow b'$, and $ s \colon b' \nrightarrow b $
then $ f \colon a \nrightarrow b$.
### Internal ordered objects
We are quite used to the idea of having an order on a set. But what about an order on a category? This is captured by $\mathbf{Ord}(E),$ the bicategory of ordered objects and ideals in a regular category $E$.
The objects of $\mathbf{Ord}(E)$ are ordered objects in $E$. An **ordered object** is a pair $(x,r)$ consisting of an $E$-object $x$ and a reflexive and transitive relation $r : x \to x$ internal to $E$.
*(Puzzle: $ r $ is a monic of type $ r \colon \hat{r} \to x \times x$. Both reflexivity and transitivity can be defined using morphisms. What are the domains and codomains? What properties should be satisfied?)*
The arrows of $\mathbf{Ord}(E)$ are a sort of 'order preserving relation' called an ideal. Precisely, an **ideal** $f \colon (x,r) \to (y,s)$ between ordered objects is a relation $f \colon x \nrightarrow y$ such that given
* morphisms $ a , a' , b , b' $ with a common domain $ z $, and
* relations $ r \colon a \nrightarrow a'$, $ f \colon a' \nrightarrow b'$, and $ s \colon b' \nrightarrow b $
then $ f \colon a \nrightarrow b$.
 In $ \mathbf{Set} $, an ordered object is a preordered set and an ideal $ f \colon (x,r) \to (y,s) $ is a directed subset of $x \times y $ with the property that if it contains $ s $ and $ s' \leq s $, then it contains $ s' $.
There is at most a single 2-cell between parallel arrows in $\mathbf{Ord}(E)$. Given $f , g \colon (x,r) \to (y,s)$, write $f \leq g$ whenever $ g \colon f_0 \nrightarrow f_1 $.
## Cartesian Bicategories
Now that we know what bicategories we have the pleasure of working with, we can move forward with the theoretical aspects. As we work through the upcoming definitions, it is helpful to recall our motivating examples $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$.
As mentioned above, in the early days of bicategory theory, mathematicians would study bicategories as $V$-enriched profunctor bicategories for some suitable $V$. A shrewd observation was made that when $V$ is Cartesian, a $V$-profunctor bicategory has several important commonalities with $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$. Namely, there is the existence of a Cartesian product $\otimes$, plus for each object $x$, a diagonal arrow $\Delta \colon x \to x \otimes x$ and terminal object $\epsilon \colon x \to I$. With this insight, Carboni and Walters decided to take this structute as primitive.
To simplify coherence, we only look at locally posetal bicategories (i.e. $\mathbf{Pos}$-enriched categories). This renders 2-dimensional coherences redundant as all parallel 2-cells manifestly commute. This assumption also endows each hom-poset with 2-cells $\leq$ and, as we will see, local meets $\wedge$. For the remainder of this article, all bicategories will be locally posetal unless otherwise stated.
**Definition.** A locally posetal bicategory $B$ is **Cartesian** when equipped with
* a symmetric tensor product $B \otimes B \to B$,
* a cocommutative comonoid structure, $\Delta_x \colon x \to x \otimes x$, and $\epsilon_x \colon x \to I$, on every $B$-object $x$
such that
* every 1-arrow $r \colon x \to y$ is a lax comonoid homomorphism, i.e.
$$
\Delta_y r \leq ( r \otimes r ) \Delta_x
\quad \text{and} \quad
\epsilon_y r \leq \epsilon_x
$$
* for all objects $x$, both $\Delta_x$ and $\epsilon_x$ have right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$.
Moreover, $(\Delta_x , \epsilon_x)$ is the *only* cocommutative comonoid structure on $x$ admitting right adjoints.
*(Question: This definition contains a slight ambiguity in the authors use of the term "moreover". Is the uniqueness property of the cocommutative comonoid structure an additional axiom or does it follow from the other axioms?)*
If you're not accustomed to thinking about adjoints internal to a general bicategory, place yourself for a moment in $\mathbf{Cat}$. Recall that adjoint functors are merely a pair of *arrows* (adjoint functors) together with a pair of *2-cells* (unit and counit) obeying certain equations. But this sort of data can exist in *any* bicategory, not just $\mathbf{Cat}$. It is worth spending a minute to feel comfortable with this concept because, in what follows, adjoints play an important role.
Observe that the right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$ turn $x$ into a commutative monoid object, hence a bimonoid. The (co)commutative (co)monoid structure on an object $x$ extend to a tensor product on $x \otimes x$ as seen in this string diagram:
In $ \mathbf{Set} $, an ordered object is a preordered set and an ideal $ f \colon (x,r) \to (y,s) $ is a directed subset of $x \times y $ with the property that if it contains $ s $ and $ s' \leq s $, then it contains $ s' $.
There is at most a single 2-cell between parallel arrows in $\mathbf{Ord}(E)$. Given $f , g \colon (x,r) \to (y,s)$, write $f \leq g$ whenever $ g \colon f_0 \nrightarrow f_1 $.
## Cartesian Bicategories
Now that we know what bicategories we have the pleasure of working with, we can move forward with the theoretical aspects. As we work through the upcoming definitions, it is helpful to recall our motivating examples $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$.
As mentioned above, in the early days of bicategory theory, mathematicians would study bicategories as $V$-enriched profunctor bicategories for some suitable $V$. A shrewd observation was made that when $V$ is Cartesian, a $V$-profunctor bicategory has several important commonalities with $\mathbf{Rel}(E)$ and $\mathbf{Ord}(E)$. Namely, there is the existence of a Cartesian product $\otimes$, plus for each object $x$, a diagonal arrow $\Delta \colon x \to x \otimes x$ and terminal object $\epsilon \colon x \to I$. With this insight, Carboni and Walters decided to take this structute as primitive.
To simplify coherence, we only look at locally posetal bicategories (i.e. $\mathbf{Pos}$-enriched categories). This renders 2-dimensional coherences redundant as all parallel 2-cells manifestly commute. This assumption also endows each hom-poset with 2-cells $\leq$ and, as we will see, local meets $\wedge$. For the remainder of this article, all bicategories will be locally posetal unless otherwise stated.
**Definition.** A locally posetal bicategory $B$ is **Cartesian** when equipped with
* a symmetric tensor product $B \otimes B \to B$,
* a cocommutative comonoid structure, $\Delta_x \colon x \to x \otimes x$, and $\epsilon_x \colon x \to I$, on every $B$-object $x$
such that
* every 1-arrow $r \colon x \to y$ is a lax comonoid homomorphism, i.e.
$$
\Delta_y r \leq ( r \otimes r ) \Delta_x
\quad \text{and} \quad
\epsilon_y r \leq \epsilon_x
$$
* for all objects $x$, both $\Delta_x$ and $\epsilon_x$ have right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$.
Moreover, $(\Delta_x , \epsilon_x)$ is the *only* cocommutative comonoid structure on $x$ admitting right adjoints.
*(Question: This definition contains a slight ambiguity in the authors use of the term "moreover". Is the uniqueness property of the cocommutative comonoid structure an additional axiom or does it follow from the other axioms?)*
If you're not accustomed to thinking about adjoints internal to a general bicategory, place yourself for a moment in $\mathbf{Cat}$. Recall that adjoint functors are merely a pair of *arrows* (adjoint functors) together with a pair of *2-cells* (unit and counit) obeying certain equations. But this sort of data can exist in *any* bicategory, not just $\mathbf{Cat}$. It is worth spending a minute to feel comfortable with this concept because, in what follows, adjoints play an important role.
Observe that the right adjoints $\Delta^\ast_x$ and $\epsilon^\ast_x$ turn $x$ into a commutative monoid object, hence a bimonoid. The (co)commutative (co)monoid structure on an object $x$ extend to a tensor product on $x \otimes x$ as seen in this string diagram:
 Ultimately, we want to think of arrows in a Cartesian bicategory as generalized relations. What other considerations are required to do this? To answer this, it is helpful to first think about what a generalized function should be.
For the moment, let's use our $\mathbf{Set}$ based intuition. For a relation to be a function, we ask that every element of the domain is related to an element of the codomain (entireness) and that the relationship is unique (determinism). How do we encode these requirements into this new, general situation? Again, let's use intuition from relations in $\mathbf{Set}$. Let $r \nrightarrow x \times y$ be a relation and $r^\circ \nrightarrow y \times x$ be the relation defined by $ r^{\circ} \colon y \nrightarrow x $ whenever $r \colon x \nrightarrow y$. To say that $r$ is entire is equivalent to saying that the composite relation $r^\circ r$ contains the identity relation on $x$ *(puzzle)*. To say that $r$ is deterministic is to say that the composite relation $rr^\circ$ is contained by the identity *(another puzzle)*. These two containments are concisely expressed by writing $1 \leq r^\circ r$ and $r r^\circ \leq 1$. Hence $r$ and $r^\circ$ form an adjoint pair! This leads us to the following definition.
**Definition.** An arrow of a Cartesian bicategory is a **map** when it has a right adjoint. Maps are closed under identity and composition. Hence, for any Cartesian bicategory $B$, there is the full subbicategory $\mathbf{Map}(B)$ whose arrows are the maps in $B$.
*(Puzzle: There is an equivalences of categories $E \simeq \mathbf{Map}(\mathbf{Rel}(E))$ for a regular category $E$. What does this say for $E := \mathbf{Set}$?)*
We can now state what appears as Theorem 1.6 of the paper. Recall that $(-)^\ast$ refers to the right adjoint.
**Theorem.** Let $B$ be a locally posetal bicategory. If $B$ is Cartesian, then
* $\mathbf{Map}(B)$ has finite biproducts $\otimes$,
* the hom-posets have finite meets $\wedge$ (i.e. categorical products) and the identity arrow in $B(I,I)$ is maximal (i.e. a terminal object), and
* biproducts and the biterminal object in $\mathbf{Map}(B)$ may be chosen so that $r \otimes s = (p^\ast r p) \wedge (p s p^\ast)$,where $p$ denotes the appropriate projection.
Conversely, if the first two properties are satisfied and the third defines a tensor product, then $B$ is Cartesian.
This theorem gives a nice characterisation of Cartesian bicategories. The first two axioms are straightforward enough, but what is the significance of the above tensor product equation?
It's actually quite painless when you break it down. Note, every biproduct $\otimes$ comes with projections $p$ and inclusions $p^\ast$. Now, let $r \colon w \to y$ and $s \colon x \to z$ which gives $r \otimes s \colon w \otimes x \to y \otimes z$. One canonical arrow of type $w \otimes x \to y \otimes z$ is $p^\ast r p$ which first projects to $w$, arrives at $y$ via $r$, which then includes into $y \otimes w$. The other arrow is similar, except we first project to $x$. The above theorem says that by combining these two arrows with a meet $\wedge$, the only available operation, we get our tensor product.
## Characterizing bicatgories of internal relations
The next stage is to add to Cartesian bicategories the property that each object is a Frobenius monoid. In this section we will study such bicategories and see that Cartesian plus Frobenius provides a reasonable axiomatization of relations.
Recall that an object with monoid and comonoid structures is called a **Frobenius monoid** if the equation
Ultimately, we want to think of arrows in a Cartesian bicategory as generalized relations. What other considerations are required to do this? To answer this, it is helpful to first think about what a generalized function should be.
For the moment, let's use our $\mathbf{Set}$ based intuition. For a relation to be a function, we ask that every element of the domain is related to an element of the codomain (entireness) and that the relationship is unique (determinism). How do we encode these requirements into this new, general situation? Again, let's use intuition from relations in $\mathbf{Set}$. Let $r \nrightarrow x \times y$ be a relation and $r^\circ \nrightarrow y \times x$ be the relation defined by $ r^{\circ} \colon y \nrightarrow x $ whenever $r \colon x \nrightarrow y$. To say that $r$ is entire is equivalent to saying that the composite relation $r^\circ r$ contains the identity relation on $x$ *(puzzle)*. To say that $r$ is deterministic is to say that the composite relation $rr^\circ$ is contained by the identity *(another puzzle)*. These two containments are concisely expressed by writing $1 \leq r^\circ r$ and $r r^\circ \leq 1$. Hence $r$ and $r^\circ$ form an adjoint pair! This leads us to the following definition.
**Definition.** An arrow of a Cartesian bicategory is a **map** when it has a right adjoint. Maps are closed under identity and composition. Hence, for any Cartesian bicategory $B$, there is the full subbicategory $\mathbf{Map}(B)$ whose arrows are the maps in $B$.
*(Puzzle: There is an equivalences of categories $E \simeq \mathbf{Map}(\mathbf{Rel}(E))$ for a regular category $E$. What does this say for $E := \mathbf{Set}$?)*
We can now state what appears as Theorem 1.6 of the paper. Recall that $(-)^\ast$ refers to the right adjoint.
**Theorem.** Let $B$ be a locally posetal bicategory. If $B$ is Cartesian, then
* $\mathbf{Map}(B)$ has finite biproducts $\otimes$,
* the hom-posets have finite meets $\wedge$ (i.e. categorical products) and the identity arrow in $B(I,I)$ is maximal (i.e. a terminal object), and
* biproducts and the biterminal object in $\mathbf{Map}(B)$ may be chosen so that $r \otimes s = (p^\ast r p) \wedge (p s p^\ast)$,where $p$ denotes the appropriate projection.
Conversely, if the first two properties are satisfied and the third defines a tensor product, then $B$ is Cartesian.
This theorem gives a nice characterisation of Cartesian bicategories. The first two axioms are straightforward enough, but what is the significance of the above tensor product equation?
It's actually quite painless when you break it down. Note, every biproduct $\otimes$ comes with projections $p$ and inclusions $p^\ast$. Now, let $r \colon w \to y$ and $s \colon x \to z$ which gives $r \otimes s \colon w \otimes x \to y \otimes z$. One canonical arrow of type $w \otimes x \to y \otimes z$ is $p^\ast r p$ which first projects to $w$, arrives at $y$ via $r$, which then includes into $y \otimes w$. The other arrow is similar, except we first project to $x$. The above theorem says that by combining these two arrows with a meet $\wedge$, the only available operation, we get our tensor product.
## Characterizing bicatgories of internal relations
The next stage is to add to Cartesian bicategories the property that each object is a Frobenius monoid. In this section we will study such bicategories and see that Cartesian plus Frobenius provides a reasonable axiomatization of relations.
Recall that an object with monoid and comonoid structures is called a **Frobenius monoid** if the equation
 holds. If you're not familiar with this equation, it has an interesting history as [outlined by Walters](http://rfcwalters.blogspot.com/2006/02/history-of-equation-1-tensor.html). Now, if every object in a Cartesian bicategory is a Frobenius monoid, we call it a **bicategory of relations**. This term is a bit overworked as it commonly refers to $\mathbf{Rel}(E)$. Therefore, we will be careful to call the latter a "bicategory of internal relations".
Why are bicatgories of relations better than simply Cartesian bicategories? For one, they admit a compact closed structure! This appears as Theorem 2.4 in the paper.
**Theorem.** A bicategory of relations has a compact closed structure. Objects are self-dual via the unit
$$
\Delta \epsilon^\ast_x \colon I \to x \otimes x
$$
and counit
$$
\epsilon \Delta^\ast_x \colon x \otimes x \to I. $$
Moreover, the dual $r^\circ$ of any arrow $r \colon x \to y$ satisfies
$$
(r \otimes id) \Delta \leq (1 \otimes r^\circ) \Delta r
$$
and
$$
\Delta^\ast (r \otimes id) \leq r \Delta^\ast (1 \otimes r^\circ).
$$
Or if you prefer string diagrams, the above inequalities are respectively
holds. If you're not familiar with this equation, it has an interesting history as [outlined by Walters](http://rfcwalters.blogspot.com/2006/02/history-of-equation-1-tensor.html). Now, if every object in a Cartesian bicategory is a Frobenius monoid, we call it a **bicategory of relations**. This term is a bit overworked as it commonly refers to $\mathbf{Rel}(E)$. Therefore, we will be careful to call the latter a "bicategory of internal relations".
Why are bicatgories of relations better than simply Cartesian bicategories? For one, they admit a compact closed structure! This appears as Theorem 2.4 in the paper.
**Theorem.** A bicategory of relations has a compact closed structure. Objects are self-dual via the unit
$$
\Delta \epsilon^\ast_x \colon I \to x \otimes x
$$
and counit
$$
\epsilon \Delta^\ast_x \colon x \otimes x \to I. $$
Moreover, the dual $r^\circ$ of any arrow $r \colon x \to y$ satisfies
$$
(r \otimes id) \Delta \leq (1 \otimes r^\circ) \Delta r
$$
and
$$
\Delta^\ast (r \otimes id) \leq r \Delta^\ast (1 \otimes r^\circ).
$$
Or if you prefer string diagrams, the above inequalities are respectively
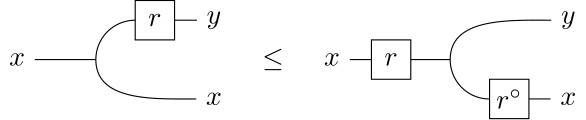 and
and
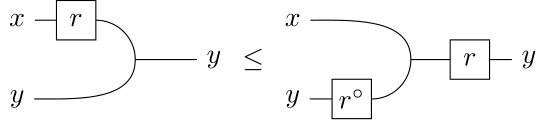 Because a bicategory of relations is Cartesian, maps are still present. In fact, they have a very nice characterization here.
**Lemma.** In a bicategory of relations, an arrow $r$ is a map iff it is a (strict) comonoid homomorphism iff $r \dashv r^\circ$.
As one would hope, the adjoint of a map corresponds with the involution coming from the compact closed structure. The following corollary provides further evidence that maps are well-behaved.
**Corollary.** In a bicategory of relations:
* $f$ is a map implies $f^\circ = f^\ast$. In particular, multiplication is adjoint to comultiplication and the unit is adjoint to the counit.
* for maps $f$ and $g$, if $f \leq g$ then $f=g$.
But maps don't merely behave in a nice way. They also contain a lot of the information about a Cartesian bicategory and, when working with bicategories of relations, the local information is quite fruitful too. This is made precise in the following corollary.
**Corollary.** Let $F \colon B \to D$ be a pseudofunctor between bicategories of relations. The following are equivalent:
* $F$ strictly preserves the Frobenius structure.
* The restriction $F \colon \mathbf{Map}(B) \to \mathbf{Map}(D)$ strictly preserves the comonoid structure.
* $F$ preserves local meets and $I$.
## Characterizing bicategories of internal relations
The entire point of the theory developed above is to be able to prove things about certain classes of bicategories. In this section, we provide a characterization theorem for bicategories of internal relations. Freyd had already given this characterization using [allegories](https://ncatlab.org/nlab/show/allegory#maps_tabulations_and_units). However, he relied on a proof by contradiction whereas using bicategories of relations allows for a constructive proof.
A bicategory of relations is meant to generalize bicategories of internal relations. Given a bicategory of relations, we'd like to know when an arrow is "like an internal relation".
**Definition.** An arrow $r \colon x \to y$ is a **tabulation** if there exists maps $f \colon z \to x$ and $g \colon z \to y$ such that $r = g f^\ast$ and $f^\ast f \wedge g^\ast g = 1_z$.
Because a bicategory of relations is Cartesian, maps are still present. In fact, they have a very nice characterization here.
**Lemma.** In a bicategory of relations, an arrow $r$ is a map iff it is a (strict) comonoid homomorphism iff $r \dashv r^\circ$.
As one would hope, the adjoint of a map corresponds with the involution coming from the compact closed structure. The following corollary provides further evidence that maps are well-behaved.
**Corollary.** In a bicategory of relations:
* $f$ is a map implies $f^\circ = f^\ast$. In particular, multiplication is adjoint to comultiplication and the unit is adjoint to the counit.
* for maps $f$ and $g$, if $f \leq g$ then $f=g$.
But maps don't merely behave in a nice way. They also contain a lot of the information about a Cartesian bicategory and, when working with bicategories of relations, the local information is quite fruitful too. This is made precise in the following corollary.
**Corollary.** Let $F \colon B \to D$ be a pseudofunctor between bicategories of relations. The following are equivalent:
* $F$ strictly preserves the Frobenius structure.
* The restriction $F \colon \mathbf{Map}(B) \to \mathbf{Map}(D)$ strictly preserves the comonoid structure.
* $F$ preserves local meets and $I$.
## Characterizing bicategories of internal relations
The entire point of the theory developed above is to be able to prove things about certain classes of bicategories. In this section, we provide a characterization theorem for bicategories of internal relations. Freyd had already given this characterization using [allegories](https://ncatlab.org/nlab/show/allegory#maps_tabulations_and_units). However, he relied on a proof by contradiction whereas using bicategories of relations allows for a constructive proof.
A bicategory of relations is meant to generalize bicategories of internal relations. Given a bicategory of relations, we'd like to know when an arrow is "like an internal relation".
**Definition.** An arrow $r \colon x \to y$ is a **tabulation** if there exists maps $f \colon z \to x$ and $g \colon z \to y$ such that $r = g f^\ast$ and $f^\ast f \wedge g^\ast g = 1_z$.
 This definition seems bizarre on its face, but it really is analogous to the jointly monic span-definition of an internal relation. That $r = g f^\ast$ is saying that $r$ is like a span $x \xleftarrow{f} z \xrightarrow{g} y$. The equation $f^\ast f \wedge g^\ast g = 1_z$ implies that this span is jointly monic *(puzzle)*.
A bicategory of relations is called **functionally complete** if every arrow $r \colon x \to I$ has a tabulation $i \colon x_r \to x$ and $t \colon x_r \to I$. One can show that the existence of these tabulations together with compact closedness is sufficient to obtain a unique (up to isomorphism) tabulation for every arrow. We now provide the characterization, presented as Theorem 3.5.
**Theorem.** Let $B$ be a functionally complete bicategory of relations. Then:
* $\mathbf{Map}(B)$ is a regular category (all 2-arrows are trivial by an above corollary)
* There is a biequivalence of bicategories $\mathbf{Rel}(\mathbf{Map}(B)) \simeq B$ obtained by sending the relation $\langle f,g \rangle$ of $\mathbf{Rel}(\mathbf{Map}(B))$ to the arrow $g f^\circ$ of $B$.
So all functionally complete bicategories of relations *are* bicategories of internal relations. An interesting quesion is whether any regular category can be realized as $\mathbf{Map}(B)$ for some functionally complete bicategory of relations. Perhaps a knowledgeable passerby will gift us with an answer in the comments!
From this theorem, we can classify some important types of categories. For instance, bicategories of relations internal to a Heyting category are exactly the functionally complete bicategory of relations having all right Kan extensions. Bicategories of relations internal to an elementary topos are exactly the functionally complete bicategories of relations $B$ such that $B(x,-)$ is representable in $\mathbf{Map}(B)$ for all objects $x$.
## Characterizing ordered object bicategories
The goal of this section is to characterize the bicategory $\mathbf{Ord}(E)$ of ordered objects and ideals. We already introduced $\mathbf{Ord}(E)$ earlier, but that definition isn't quite abstract enough for our purposes. An equivalent way of defining an ordered object in $E$ is as an $E$-object $x$ together with a relation $r$ on $x$ such that $1 \leq r$ and $r r \leq r$. Does this data look familiar? An ordered object in $E$ is simply a monad in $\mathbf{Rel}(E)$!
*(Puzzle: What is a monad in a general bicategory? Hint: how are adjoints defined in a general bicategory?)*
Quite a bit is known about monads, and we can now apply that knowledge to our study of $\mathbf{Ord}(E)$.
Recall that any monad in $\mathbf{Cat}$ gives rise to a category of adjunctions. The initial object of this category is the Kleisli category. Since the Kleisli category can be defined using a universal property, we can define a Kleisli object in any bicategory. In general, a Kleisli object for a monad $t \colon x \to x$ need not exist but when it does, it is defined as an arrow $k : x \to x_t$ plus a 2-arrow $\theta \colon k t \to k$ such that, given any arrow $f \colon x \to y$ and 2-arrow $\alpha \colon f t \to f$, there exists a unique arrow $h \colon x_t \to y$ such that $h k = f$. The pasting diagrams involved also commute:
This definition seems bizarre on its face, but it really is analogous to the jointly monic span-definition of an internal relation. That $r = g f^\ast$ is saying that $r$ is like a span $x \xleftarrow{f} z \xrightarrow{g} y$. The equation $f^\ast f \wedge g^\ast g = 1_z$ implies that this span is jointly monic *(puzzle)*.
A bicategory of relations is called **functionally complete** if every arrow $r \colon x \to I$ has a tabulation $i \colon x_r \to x$ and $t \colon x_r \to I$. One can show that the existence of these tabulations together with compact closedness is sufficient to obtain a unique (up to isomorphism) tabulation for every arrow. We now provide the characterization, presented as Theorem 3.5.
**Theorem.** Let $B$ be a functionally complete bicategory of relations. Then:
* $\mathbf{Map}(B)$ is a regular category (all 2-arrows are trivial by an above corollary)
* There is a biequivalence of bicategories $\mathbf{Rel}(\mathbf{Map}(B)) \simeq B$ obtained by sending the relation $\langle f,g \rangle$ of $\mathbf{Rel}(\mathbf{Map}(B))$ to the arrow $g f^\circ$ of $B$.
So all functionally complete bicategories of relations *are* bicategories of internal relations. An interesting quesion is whether any regular category can be realized as $\mathbf{Map}(B)$ for some functionally complete bicategory of relations. Perhaps a knowledgeable passerby will gift us with an answer in the comments!
From this theorem, we can classify some important types of categories. For instance, bicategories of relations internal to a Heyting category are exactly the functionally complete bicategory of relations having all right Kan extensions. Bicategories of relations internal to an elementary topos are exactly the functionally complete bicategories of relations $B$ such that $B(x,-)$ is representable in $\mathbf{Map}(B)$ for all objects $x$.
## Characterizing ordered object bicategories
The goal of this section is to characterize the bicategory $\mathbf{Ord}(E)$ of ordered objects and ideals. We already introduced $\mathbf{Ord}(E)$ earlier, but that definition isn't quite abstract enough for our purposes. An equivalent way of defining an ordered object in $E$ is as an $E$-object $x$ together with a relation $r$ on $x$ such that $1 \leq r$ and $r r \leq r$. Does this data look familiar? An ordered object in $E$ is simply a monad in $\mathbf{Rel}(E)$!
*(Puzzle: What is a monad in a general bicategory? Hint: how are adjoints defined in a general bicategory?)*
Quite a bit is known about monads, and we can now apply that knowledge to our study of $\mathbf{Ord}(E)$.
Recall that any monad in $\mathbf{Cat}$ gives rise to a category of adjunctions. The initial object of this category is the Kleisli category. Since the Kleisli category can be defined using a universal property, we can define a Kleisli object in any bicategory. In general, a Kleisli object for a monad $t \colon x \to x$ need not exist but when it does, it is defined as an arrow $k : x \to x_t$ plus a 2-arrow $\theta \colon k t \to k$ such that, given any arrow $f \colon x \to y$ and 2-arrow $\alpha \colon f t \to f$, there exists a unique arrow $h \colon x_t \to y$ such that $h k = f$. The pasting diagrams involved also commute:
 As in the case of working inside $\mathbf{Cat}$, we would expect for $k$ to be on the left of an adjoint pair, and indeed it is. We get a right adjoint $k^\ast$ such that the composite $k^\ast k$ is our original monad $t$. The benefit of working in the locally posetal case is we also have that $k k^\ast = 1$. This realizes $t$ as an idempotent:
$$ t t
= k^\ast k k^\ast k
= k^\ast k
= t. $$
It follows that the Kleisli object construction is exactly an idempotent splitting of $t$! This means we can start with an exact category $E$ and construct $\mathbf{Ord}(E)$ by splitting the idempotents of $\mathbf{Rel}(E)$. With this in mind, we move on to the characterization, presented as Theorem 4.6.
**Theorem.** A bicategory $B$ is biequivalent to a bicategory $\mathbf{Ord}(E)$ if and only if
* $B$ is Cartesian,
* every monad in $B$ has a Kleisli object,
* for each object $x$, there is a monad on $x$ and a Frobenius monoid $x_0$ that is isomorphic to the monad's Kleisli object,
* given a Frobenius monoid x and $f \colon x \to x$ with $f \leq 1$, $f$ splits.
## Final words
The authors go on to look closer at bicategories of relations inside Grothendieck topoi and abelian categories. Both of these are regular categories, and so fit into the picture we've just painted. However, each have additional properties and structure that compels further study.
Much of what we have done can be done in greater generality. For instance, we can drop the local posetal requirement. However, this would greatly complicate matters by requiring non-trivial coherence conditions.
As in the case of working inside $\mathbf{Cat}$, we would expect for $k$ to be on the left of an adjoint pair, and indeed it is. We get a right adjoint $k^\ast$ such that the composite $k^\ast k$ is our original monad $t$. The benefit of working in the locally posetal case is we also have that $k k^\ast = 1$. This realizes $t$ as an idempotent:
$$ t t
= k^\ast k k^\ast k
= k^\ast k
= t. $$
It follows that the Kleisli object construction is exactly an idempotent splitting of $t$! This means we can start with an exact category $E$ and construct $\mathbf{Ord}(E)$ by splitting the idempotents of $\mathbf{Rel}(E)$. With this in mind, we move on to the characterization, presented as Theorem 4.6.
**Theorem.** A bicategory $B$ is biequivalent to a bicategory $\mathbf{Ord}(E)$ if and only if
* $B$ is Cartesian,
* every monad in $B$ has a Kleisli object,
* for each object $x$, there is a monad on $x$ and a Frobenius monoid $x_0$ that is isomorphic to the monad's Kleisli object,
* given a Frobenius monoid x and $f \colon x \to x$ with $f \leq 1$, $f$ splits.
## Final words
The authors go on to look closer at bicategories of relations inside Grothendieck topoi and abelian categories. Both of these are regular categories, and so fit into the picture we've just painted. However, each have additional properties and structure that compels further study.
Much of what we have done can be done in greater generality. For instance, we can drop the local posetal requirement. However, this would greatly complicate matters by requiring non-trivial coherence conditions.