*guest post by [Joseph Moeller](http://math.ucr.edu/~moeller/) and [Dmitry Vagner](https://math.duke.edu/people/dmitry-vagner)*
We begin the [Applied Category Theory Seminar](http://www.appliedcategorytheory.org/school/) by discussing the paper [A categorical semantics for causal structure](https://arxiv.org/abs/1701.04732) by Aleks Kissinger and Sander Uijlen.
Compact closed categories have been used in categorical quantum mechanics to give a structure for talking about quantum processes. However, they prove insufficient to handle higher order processes, in other words, processes of processes. This paper offers a construction for a $\ast$-autonomous extension of a given compact closed category which allows one to reason about higher order processes in a non-trivial way.
We would like to thank Brendan Fong, Nina Otter, Joseph Hirsh and Tobias Heindel as well as the other participants for the discussions and feedback.
## Preliminaries
We begin with a discussion about the types of categories which we will be working with, and the diagrammatic language we use to reason about these categories.
### Diagrammatics
Recall the following diagrammatic language we use to reason about symmetric monoidal categories. Objects are represented by wires. Arrows can be graphically encoded as
>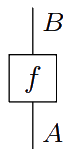 Composition $\circ$ and $\otimes$ depicted vertically and horizontally
>
Composition $\circ$ and $\otimes$ depicted vertically and horizontally
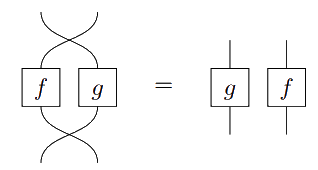
>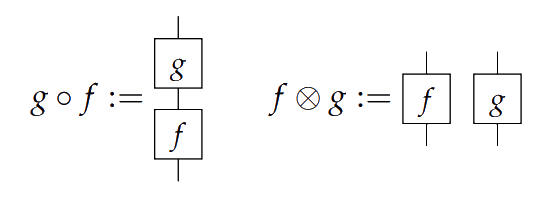 satisfying the properties
>
satisfying the properties
>
 and the interchange law
>
and the interchange law
> If $I$ is the unit object, and $A$ is an object, we call arrows $I \to A$ **states**, $A \to I$ **effects**, and $I \to I$ **numbers**.
>
If $I$ is the unit object, and $A$ is an object, we call arrows $I \to A$ **states**, $A \to I$ **effects**, and $I \to I$ **numbers**.
>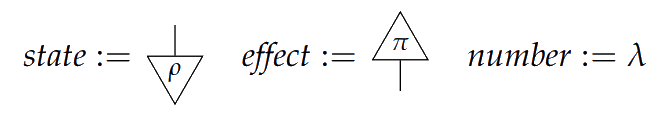 The identity morphism on an object is only displayed as a wire, and both $I$ and its identity morphism are not displayed.
>
The identity morphism on an object is only displayed as a wire, and both $I$ and its identity morphism are not displayed.
>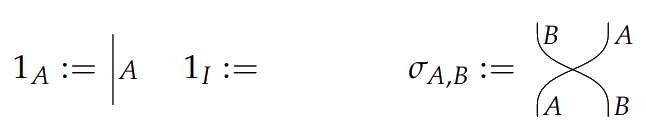 ### Compact closed categories
A symmetric monoidal category is **compact closed** if each object $A$ has a dual object $A^\ast$ with arrows
$$\eta_A \colon I \to A^\ast \otimes A,$$
and
$$\epsilon_A \colon A \otimes A^\ast \to I,$$
depicted as $\cup$ and $\cap$ and obeying the **zigzag identities**:
>
### Compact closed categories
A symmetric monoidal category is **compact closed** if each object $A$ has a dual object $A^\ast$ with arrows
$$\eta_A \colon I \to A^\ast \otimes A,$$
and
$$\epsilon_A \colon A \otimes A^\ast \to I,$$
depicted as $\cup$ and $\cap$ and obeying the **zigzag identities**:
>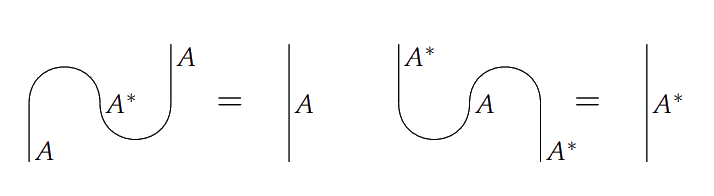 Given a process $f \colon A \to B$ in a compact closed category, we can construct a state $\rho_f \colon I \to A^\ast \otimes B$ by defining
$$\rho_f = (1_{A^\ast} \otimes f) \circ \eta_A.$$
>
Given a process $f \colon A \to B$ in a compact closed category, we can construct a state $\rho_f \colon I \to A^\ast \otimes B$ by defining
$$\rho_f = (1_{A^\ast} \otimes f) \circ \eta_A.$$
>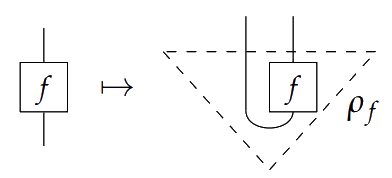 This gives a correspondence which is called "process-state duality".
### An example
Let $Mat(\mathbb{R}_+)$ be the category in which objects are natural numbers, and morphisms $m \to n$ are $n\times m$ $\mathbb{R}_+$-matrices with composition given by the usual multiplication of matrices. This category is made symmetric monoidal with tensor defined by $n \otimes m = nm$ on objects and the Kronecker product of matrices on arrows, $(f \otimes g)^{kl}_{ij} = f^k_i g^l_j$. For example
$$
\begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}
\otimes
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
=
\begin{bmatrix}
1\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&
2\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\\
3 \cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&4\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
0 & 5 & 0 & 10 \\
6 & 7 & 12 & 14 \\
0 & 15 & 0 & 20 \\
18 & 21 & 24 & 28
\end{bmatrix}
$$
The unit with respect to this tensor is $1$.
States in this category are column vectors, effects are row vectors, and numbers are $1\times 1$ matrices, in other words, numbers.
Composing a state $\rho\colon 1 \to n$ with an effect $\pi\colon n \to 1$, is the dot product.
To define a compact closed structure on this category, let $n^\ast := n$. Then $\eta_n \colon 1 \to n^2$ and $\varepsilon_n \colon n^2 \to 1$ are given by the Kronecker delta.
## A Categorical Framework for Causality
### Encoding causality
The main construction in this paper requires what is called a *precausal* category. In a precausal category, we demand that every system has a **discard effect**, which is a process
This gives a correspondence which is called "process-state duality".
### An example
Let $Mat(\mathbb{R}_+)$ be the category in which objects are natural numbers, and morphisms $m \to n$ are $n\times m$ $\mathbb{R}_+$-matrices with composition given by the usual multiplication of matrices. This category is made symmetric monoidal with tensor defined by $n \otimes m = nm$ on objects and the Kronecker product of matrices on arrows, $(f \otimes g)^{kl}_{ij} = f^k_i g^l_j$. For example
$$
\begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}
\otimes
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
=
\begin{bmatrix}
1\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&
2\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\\
3 \cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&4\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
0 & 5 & 0 & 10 \\
6 & 7 & 12 & 14 \\
0 & 15 & 0 & 20 \\
18 & 21 & 24 & 28
\end{bmatrix}
$$
The unit with respect to this tensor is $1$.
States in this category are column vectors, effects are row vectors, and numbers are $1\times 1$ matrices, in other words, numbers.
Composing a state $\rho\colon 1 \to n$ with an effect $\pi\colon n \to 1$, is the dot product.
To define a compact closed structure on this category, let $n^\ast := n$. Then $\eta_n \colon 1 \to n^2$ and $\varepsilon_n \colon n^2 \to 1$ are given by the Kronecker delta.
## A Categorical Framework for Causality
### Encoding causality
The main construction in this paper requires what is called a *precausal* category. In a precausal category, we demand that every system has a **discard effect**, which is a process  $_A \colon A \to I$. This collection of effects must be compatible with $\otimes$:
*
$_A \colon A \to I$. This collection of effects must be compatible with $\otimes$:
*  $_{A \otimes B} = $
$_{A \otimes B} = $ $_A $
$_A $ $_B$
*
$_B$
*  $_I = 1$
A process $\Phi \colon A \to B$ is called **causal** if discarding $B$ after having done $\Phi$ is the same as just discarding $A$.
>
$_I = 1$
A process $\Phi \colon A \to B$ is called **causal** if discarding $B$ after having done $\Phi$ is the same as just discarding $A$.
>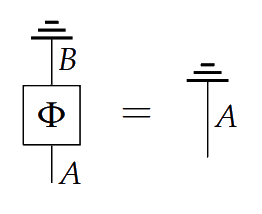 If $A^\ast$ has discarding, we can produce a state for $A$ by spawning an $A$ and $A^\ast$ pair, then discarding the $A^\ast$:
>
If $A^\ast$ has discarding, we can produce a state for $A$ by spawning an $A$ and $A^\ast$ pair, then discarding the $A^\ast$:
>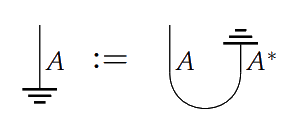 In the case of $Mat(\mathbb{R}_+)$, the discard effect is given as row vector of $1$'s: $\mathbf{1}:=(1\cdots 1)$. Composing a matrix with the discard effect sums the entries of each column. So if a matrix is a causal process, then its column vectors have entries that sum to $1$. Thus causal processes in $Mat(\mathbb{R}_+)$ are stochastic maps.
A process $\Phi \colon A \otimes B \to A' \otimes B'$ is **one-way signalling** with $A \preceq B$ if
>
In the case of $Mat(\mathbb{R}_+)$, the discard effect is given as row vector of $1$'s: $\mathbf{1}:=(1\cdots 1)$. Composing a matrix with the discard effect sums the entries of each column. So if a matrix is a causal process, then its column vectors have entries that sum to $1$. Thus causal processes in $Mat(\mathbb{R}_+)$ are stochastic maps.
A process $\Phi \colon A \otimes B \to A' \otimes B'$ is **one-way signalling** with $A \preceq B$ if
>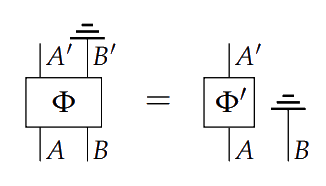 and $B \preceq A$ if
>
and $B \preceq A$ if
>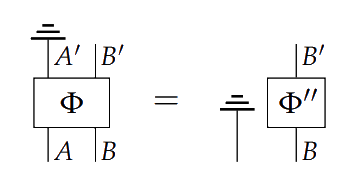 and **non-signalling** if both $A\preceq B$ and $B\preceq A$.
The intuition here is that $A \preceq B$ means $B$ cannot signal to $A$; the formal condition encodes the fact that had $B$ influenced the transformation from $A$ to $A'$, then it couldn't have been discarded prior to it occurring.
Consider the following example: let $A$ be a cup of tea, and $B$ a glass of milk. Let $\Phi$ the process of pouring half of $B$ into $A$ then mixing, to form $A'$ milktea and $B'$ half-glass of milk. Clearly this process would not be the same as if we start by discarding the milk. Our intuition is that the milk "signalled" to, or influenced, the tea, and hence intuitively we do not have $A \preceq B$.
A compact closed category $\C$ is **precausal** if
1) Every system $A$ has a discard process
and **non-signalling** if both $A\preceq B$ and $B\preceq A$.
The intuition here is that $A \preceq B$ means $B$ cannot signal to $A$; the formal condition encodes the fact that had $B$ influenced the transformation from $A$ to $A'$, then it couldn't have been discarded prior to it occurring.
Consider the following example: let $A$ be a cup of tea, and $B$ a glass of milk. Let $\Phi$ the process of pouring half of $B$ into $A$ then mixing, to form $A'$ milktea and $B'$ half-glass of milk. Clearly this process would not be the same as if we start by discarding the milk. Our intuition is that the milk "signalled" to, or influenced, the tea, and hence intuitively we do not have $A \preceq B$.
A compact closed category $\C$ is **precausal** if
1) Every system $A$ has a discard process  $_A$
2) For every system $A$, the **dimension** is invertible
>
$_A$
2) For every system $A$, the **dimension** is invertible
>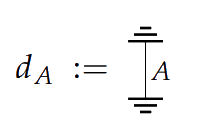 3) $\C$ has **enough causal states**
>
3) $\C$ has **enough causal states**
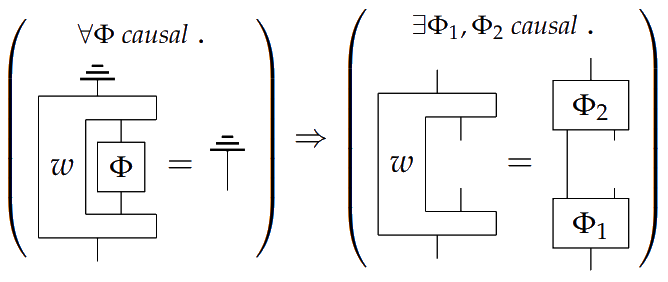
>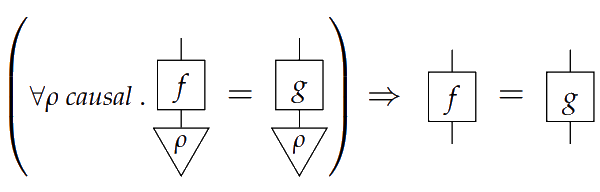 4) **Second order causal processes factor**
>
4) **Second order causal processes factor**
> From the definition, we can begin to exclude certain causal situations from systems in precausal categories. In Theorem 3.12, we see that precausal categories do not admit 'time-travel'.
> **Theorem** *If there are systems $A$, $B$, $C$ such that*
>
From the definition, we can begin to exclude certain causal situations from systems in precausal categories. In Theorem 3.12, we see that precausal categories do not admit 'time-travel'.
> **Theorem** *If there are systems $A$, $B$, $C$ such that*
>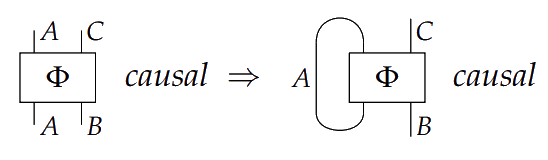 >*then $A \cong I$.*
In precausal categories, we have processes that we call *first order causal*. However, higher order processes collapse into first order processes, because precausal categories are compact closed.
For example, letting $A \Rightarrow B := A^\ast\otimes B$,
$$
(A\Rightarrow B)\Rightarrow C = (A^\ast\otimes B)\ast\otimes C
\cong B\Rightarrow A\otimes C
$$
We can see this happens because of the condition $A \otimes B \cong (A^\ast \otimes B^\ast)^\ast$. Weakening this condition of compact closed categories yields $\ast$-autonomous categories. From a precausal category $\C$, we construct a category $Caus[\C]$ of higher order causal relations.
### The category of higher order causal processes
Given a set of states $c \subseteq \C(I,A)$ for a system $A$, define its dual by
$$
c^\ast = \{\pi \in A^\ast |\, \forall \rho \in c ,\, \pi \circ \rho = 1\} \subseteq \C(I, A^\ast)
$$
Then we say a set of states $c \subseteq \C(I,A)$ is **closed** if $c=c^{\ast\ast}$, and **flat** if there are invertible scalars $\lambda$, $\mu$ such that $\lambda$
>*then $A \cong I$.*
In precausal categories, we have processes that we call *first order causal*. However, higher order processes collapse into first order processes, because precausal categories are compact closed.
For example, letting $A \Rightarrow B := A^\ast\otimes B$,
$$
(A\Rightarrow B)\Rightarrow C = (A^\ast\otimes B)\ast\otimes C
\cong B\Rightarrow A\otimes C
$$
We can see this happens because of the condition $A \otimes B \cong (A^\ast \otimes B^\ast)^\ast$. Weakening this condition of compact closed categories yields $\ast$-autonomous categories. From a precausal category $\C$, we construct a category $Caus[\C]$ of higher order causal relations.
### The category of higher order causal processes
Given a set of states $c \subseteq \C(I,A)$ for a system $A$, define its dual by
$$
c^\ast = \{\pi \in A^\ast |\, \forall \rho \in c ,\, \pi \circ \rho = 1\} \subseteq \C(I, A^\ast)
$$
Then we say a set of states $c \subseteq \C(I,A)$ is **closed** if $c=c^{\ast\ast}$, and **flat** if there are invertible scalars $\lambda$, $\mu$ such that $\lambda$ 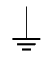 $\in c$, $\mu$
$\in c$, $\mu$  $\in c^\ast$.
Now we can define the category $Caus[\C]$. Let the objects be pairs $(A, c_A)$ where $c_A$ is a closed and flat set of states of the system $A \in \C$. A morphism $f \colon (A, c_A) \to (B, c_B)$ is a morphism $f \colon A \to B$ in $\C$ such that if $\rho \in c_A$, then $f \circ \rho \in c_B$. This category is a symmetric monoidal category with $(A, c_A) \otimes (B, c_B) = (A \otimes B, c_{A \otimes B})$. Further, it's $\ast$-autonomous, so higher order processes won't necessarily collapse into first order.
A **first order** system in $Caus[\C]$ is one of the form $(A, \{$
$\in c^\ast$.
Now we can define the category $Caus[\C]$. Let the objects be pairs $(A, c_A)$ where $c_A$ is a closed and flat set of states of the system $A \in \C$. A morphism $f \colon (A, c_A) \to (B, c_B)$ is a morphism $f \colon A \to B$ in $\C$ such that if $\rho \in c_A$, then $f \circ \rho \in c_B$. This category is a symmetric monoidal category with $(A, c_A) \otimes (B, c_B) = (A \otimes B, c_{A \otimes B})$. Further, it's $\ast$-autonomous, so higher order processes won't necessarily collapse into first order.
A **first order** system in $Caus[\C]$ is one of the form $(A, \{$ $_A\}^\ast)$. First order systems are closed under $\otimes$. In fact, $C_C$ admits a full faithful monoidal embedding into $Caus[\C]$ by assigning systems to their corresponding first order systems $A \mapsto (A, \{$
$_A\}^\ast)$. First order systems are closed under $\otimes$. In fact, $C_C$ admits a full faithful monoidal embedding into $Caus[\C]$ by assigning systems to their corresponding first order systems $A \mapsto (A, \{$ $_A\})$.
For an example of a higher order process in $Caus[Mat(\mathbb{R}_+)]$, consider a classical switch. Let
$$\rho_0 = \begin{bmatrix}
1\\0
\end{bmatrix},
\quad
\rho_1 = \begin{bmatrix}
0\\1
\end{bmatrix},
\quad
\rho'_i = \rho_i^T,$$
and let $s$ be the second order process
$_A\})$.
For an example of a higher order process in $Caus[Mat(\mathbb{R}_+)]$, consider a classical switch. Let
$$\rho_0 = \begin{bmatrix}
1\\0
\end{bmatrix},
\quad
\rho_1 = \begin{bmatrix}
0\\1
\end{bmatrix},
\quad
\rho'_i = \rho_i^T,$$
and let $s$ be the second order process
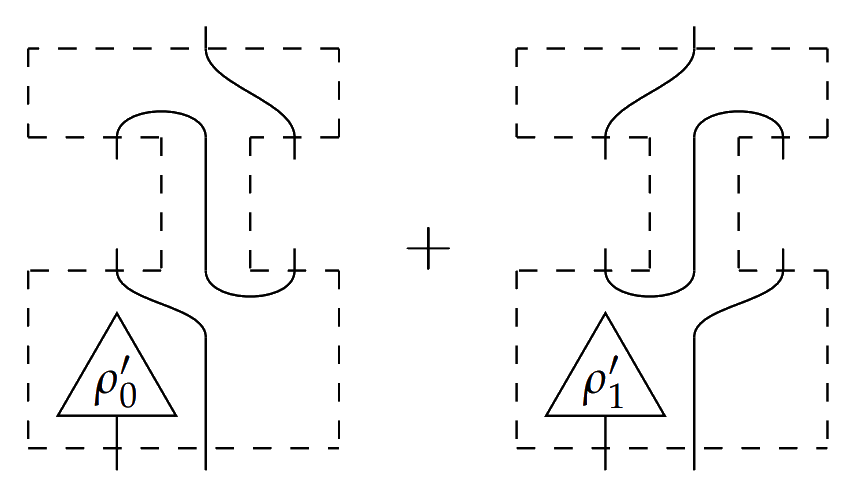 This process is of type $X \otimes C \multimap (A \multimap B) \otimes (B \multimap A) \multimap C'$, where the two middle inputs take types $A \multimap B$ on the left and $B \multimap A$ on the right. Since $\rho'_i \circ \rho_j$ is $1$ if $i=j$ and $0$ otherwise, then plugging in either $\rho_0$ or $\rho_1$ to the bottom left input *switches* the order that the $A \multimap B$ and $B \multimap A$ processes are composed in the final output process. This second order process is causal because
This process is of type $X \otimes C \multimap (A \multimap B) \otimes (B \multimap A) \multimap C'$, where the two middle inputs take types $A \multimap B$ on the left and $B \multimap A$ on the right. Since $\rho'_i \circ \rho_j$ is $1$ if $i=j$ and $0$ otherwise, then plugging in either $\rho_0$ or $\rho_1$ to the bottom left input *switches* the order that the $A \multimap B$ and $B \multimap A$ processes are composed in the final output process. This second order process is causal because
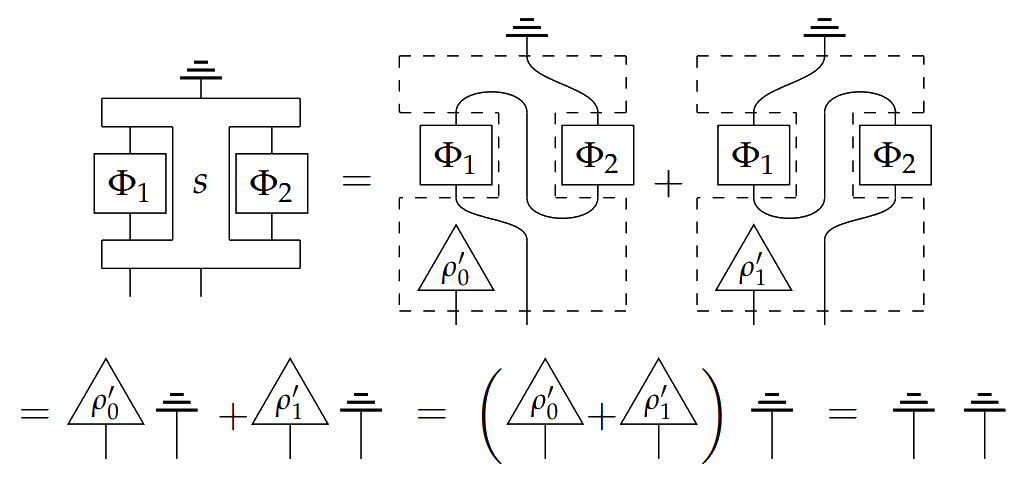 The authors go on to prove in Theorem 6.17 that a switch cannot be causally ordered, indicating that this process is genuinely second order.
The authors go on to prove in Theorem 6.17 that a switch cannot be causally ordered, indicating that this process is genuinely second order.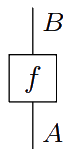 Composition $\circ$ and $\otimes$ depicted vertically and horizontally
>
Composition $\circ$ and $\otimes$ depicted vertically and horizontally
>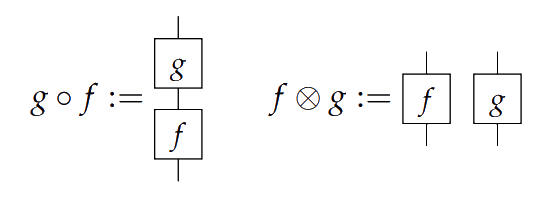 satisfying the properties
>
satisfying the properties
>
 and the interchange law
>
and the interchange law
>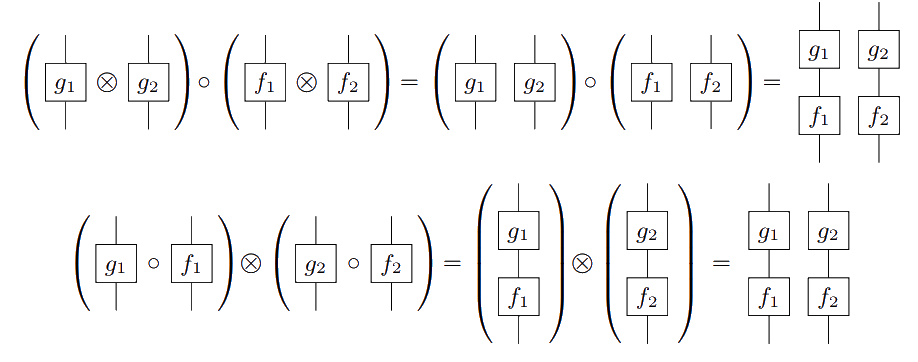 If $I$ is the unit object, and $A$ is an object, we call arrows $I \to A$ **states**, $A \to I$ **effects**, and $I \to I$ **numbers**.
>
If $I$ is the unit object, and $A$ is an object, we call arrows $I \to A$ **states**, $A \to I$ **effects**, and $I \to I$ **numbers**.
>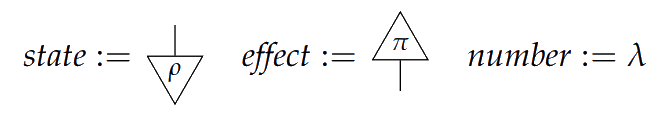 The identity morphism on an object is only displayed as a wire, and both $I$ and its identity morphism are not displayed.
>
The identity morphism on an object is only displayed as a wire, and both $I$ and its identity morphism are not displayed.
>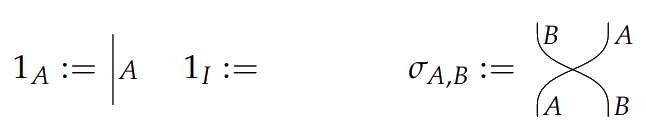 ### Compact closed categories
A symmetric monoidal category is **compact closed** if each object $A$ has a dual object $A^\ast$ with arrows
$$\eta_A \colon I \to A^\ast \otimes A,$$
and
$$\epsilon_A \colon A \otimes A^\ast \to I,$$
depicted as $\cup$ and $\cap$ and obeying the **zigzag identities**:
>
### Compact closed categories
A symmetric monoidal category is **compact closed** if each object $A$ has a dual object $A^\ast$ with arrows
$$\eta_A \colon I \to A^\ast \otimes A,$$
and
$$\epsilon_A \colon A \otimes A^\ast \to I,$$
depicted as $\cup$ and $\cap$ and obeying the **zigzag identities**:
>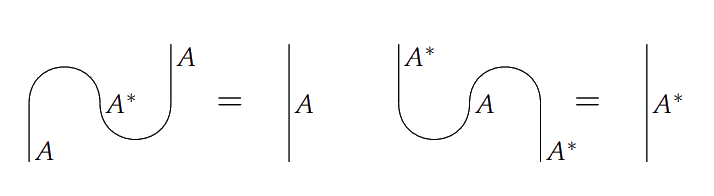 Given a process $f \colon A \to B$ in a compact closed category, we can construct a state $\rho_f \colon I \to A^\ast \otimes B$ by defining
$$\rho_f = (1_{A^\ast} \otimes f) \circ \eta_A.$$
>
Given a process $f \colon A \to B$ in a compact closed category, we can construct a state $\rho_f \colon I \to A^\ast \otimes B$ by defining
$$\rho_f = (1_{A^\ast} \otimes f) \circ \eta_A.$$
> This gives a correspondence which is called "process-state duality".
### An example
Let $Mat(\mathbb{R}_+)$ be the category in which objects are natural numbers, and morphisms $m \to n$ are $n\times m$ $\mathbb{R}_+$-matrices with composition given by the usual multiplication of matrices. This category is made symmetric monoidal with tensor defined by $n \otimes m = nm$ on objects and the Kronecker product of matrices on arrows, $(f \otimes g)^{kl}_{ij} = f^k_i g^l_j$. For example
$$
\begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}
\otimes
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
=
\begin{bmatrix}
1\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&
2\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\\
3 \cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&4\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
0 & 5 & 0 & 10 \\
6 & 7 & 12 & 14 \\
0 & 15 & 0 & 20 \\
18 & 21 & 24 & 28
\end{bmatrix}
$$
The unit with respect to this tensor is $1$.
States in this category are column vectors, effects are row vectors, and numbers are $1\times 1$ matrices, in other words, numbers.
Composing a state $\rho\colon 1 \to n$ with an effect $\pi\colon n \to 1$, is the dot product.
To define a compact closed structure on this category, let $n^\ast := n$. Then $\eta_n \colon 1 \to n^2$ and $\varepsilon_n \colon n^2 \to 1$ are given by the Kronecker delta.
## A Categorical Framework for Causality
### Encoding causality
The main construction in this paper requires what is called a *precausal* category. In a precausal category, we demand that every system has a **discard effect**, which is a process
This gives a correspondence which is called "process-state duality".
### An example
Let $Mat(\mathbb{R}_+)$ be the category in which objects are natural numbers, and morphisms $m \to n$ are $n\times m$ $\mathbb{R}_+$-matrices with composition given by the usual multiplication of matrices. This category is made symmetric monoidal with tensor defined by $n \otimes m = nm$ on objects and the Kronecker product of matrices on arrows, $(f \otimes g)^{kl}_{ij} = f^k_i g^l_j$. For example
$$
\begin{bmatrix}
1 & 2 \\
3 & 4
\end{bmatrix}
\otimes
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
=
\begin{bmatrix}
1\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&
2\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\\
3 \cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
&4\cdot
\begin{bmatrix}
0 & 5 \\
6 & 7
\end{bmatrix}
\end{bmatrix}
=
\begin{bmatrix}
0 & 5 & 0 & 10 \\
6 & 7 & 12 & 14 \\
0 & 15 & 0 & 20 \\
18 & 21 & 24 & 28
\end{bmatrix}
$$
The unit with respect to this tensor is $1$.
States in this category are column vectors, effects are row vectors, and numbers are $1\times 1$ matrices, in other words, numbers.
Composing a state $\rho\colon 1 \to n$ with an effect $\pi\colon n \to 1$, is the dot product.
To define a compact closed structure on this category, let $n^\ast := n$. Then $\eta_n \colon 1 \to n^2$ and $\varepsilon_n \colon n^2 \to 1$ are given by the Kronecker delta.
## A Categorical Framework for Causality
### Encoding causality
The main construction in this paper requires what is called a *precausal* category. In a precausal category, we demand that every system has a **discard effect**, which is a process 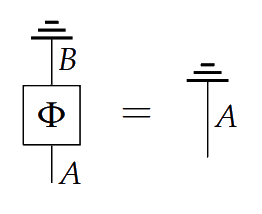 If $A^\ast$ has discarding, we can produce a state for $A$ by spawning an $A$ and $A^\ast$ pair, then discarding the $A^\ast$:
>
If $A^\ast$ has discarding, we can produce a state for $A$ by spawning an $A$ and $A^\ast$ pair, then discarding the $A^\ast$:
>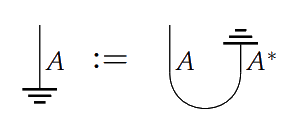 In the case of $Mat(\mathbb{R}_+)$, the discard effect is given as row vector of $1$'s: $\mathbf{1}:=(1\cdots 1)$. Composing a matrix with the discard effect sums the entries of each column. So if a matrix is a causal process, then its column vectors have entries that sum to $1$. Thus causal processes in $Mat(\mathbb{R}_+)$ are stochastic maps.
A process $\Phi \colon A \otimes B \to A' \otimes B'$ is **one-way signalling** with $A \preceq B$ if
>
In the case of $Mat(\mathbb{R}_+)$, the discard effect is given as row vector of $1$'s: $\mathbf{1}:=(1\cdots 1)$. Composing a matrix with the discard effect sums the entries of each column. So if a matrix is a causal process, then its column vectors have entries that sum to $1$. Thus causal processes in $Mat(\mathbb{R}_+)$ are stochastic maps.
A process $\Phi \colon A \otimes B \to A' \otimes B'$ is **one-way signalling** with $A \preceq B$ if
>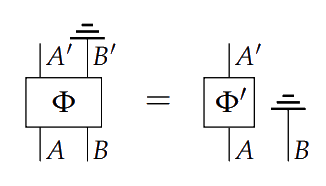 and $B \preceq A$ if
>
and $B \preceq A$ if
>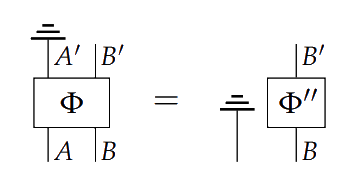 and **non-signalling** if both $A\preceq B$ and $B\preceq A$.
The intuition here is that $A \preceq B$ means $B$ cannot signal to $A$; the formal condition encodes the fact that had $B$ influenced the transformation from $A$ to $A'$, then it couldn't have been discarded prior to it occurring.
Consider the following example: let $A$ be a cup of tea, and $B$ a glass of milk. Let $\Phi$ the process of pouring half of $B$ into $A$ then mixing, to form $A'$ milktea and $B'$ half-glass of milk. Clearly this process would not be the same as if we start by discarding the milk. Our intuition is that the milk "signalled" to, or influenced, the tea, and hence intuitively we do not have $A \preceq B$.
A compact closed category $\C$ is **precausal** if
1) Every system $A$ has a discard process
and **non-signalling** if both $A\preceq B$ and $B\preceq A$.
The intuition here is that $A \preceq B$ means $B$ cannot signal to $A$; the formal condition encodes the fact that had $B$ influenced the transformation from $A$ to $A'$, then it couldn't have been discarded prior to it occurring.
Consider the following example: let $A$ be a cup of tea, and $B$ a glass of milk. Let $\Phi$ the process of pouring half of $B$ into $A$ then mixing, to form $A'$ milktea and $B'$ half-glass of milk. Clearly this process would not be the same as if we start by discarding the milk. Our intuition is that the milk "signalled" to, or influenced, the tea, and hence intuitively we do not have $A \preceq B$.
A compact closed category $\C$ is **precausal** if
1) Every system $A$ has a discard process 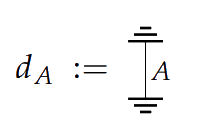 3) $\C$ has **enough causal states**
>
3) $\C$ has **enough causal states**
>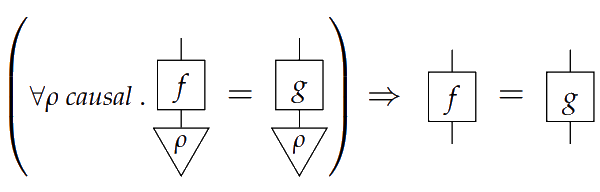 4) **Second order causal processes factor**
>
4) **Second order causal processes factor**
> From the definition, we can begin to exclude certain causal situations from systems in precausal categories. In Theorem 3.12, we see that precausal categories do not admit 'time-travel'.
> **Theorem** *If there are systems $A$, $B$, $C$ such that*
>
From the definition, we can begin to exclude certain causal situations from systems in precausal categories. In Theorem 3.12, we see that precausal categories do not admit 'time-travel'.
> **Theorem** *If there are systems $A$, $B$, $C$ such that*
>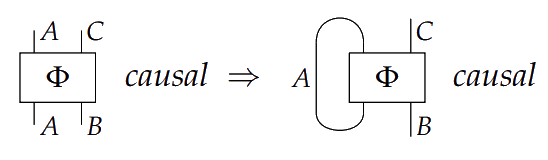 >*then $A \cong I$.*
In precausal categories, we have processes that we call *first order causal*. However, higher order processes collapse into first order processes, because precausal categories are compact closed.
For example, letting $A \Rightarrow B := A^\ast\otimes B$,
$$
(A\Rightarrow B)\Rightarrow C = (A^\ast\otimes B)\ast\otimes C
\cong B\Rightarrow A\otimes C
$$
We can see this happens because of the condition $A \otimes B \cong (A^\ast \otimes B^\ast)^\ast$. Weakening this condition of compact closed categories yields $\ast$-autonomous categories. From a precausal category $\C$, we construct a category $Caus[\C]$ of higher order causal relations.
### The category of higher order causal processes
Given a set of states $c \subseteq \C(I,A)$ for a system $A$, define its dual by
$$
c^\ast = \{\pi \in A^\ast |\, \forall \rho \in c ,\, \pi \circ \rho = 1\} \subseteq \C(I, A^\ast)
$$
Then we say a set of states $c \subseteq \C(I,A)$ is **closed** if $c=c^{\ast\ast}$, and **flat** if there are invertible scalars $\lambda$, $\mu$ such that $\lambda$
>*then $A \cong I$.*
In precausal categories, we have processes that we call *first order causal*. However, higher order processes collapse into first order processes, because precausal categories are compact closed.
For example, letting $A \Rightarrow B := A^\ast\otimes B$,
$$
(A\Rightarrow B)\Rightarrow C = (A^\ast\otimes B)\ast\otimes C
\cong B\Rightarrow A\otimes C
$$
We can see this happens because of the condition $A \otimes B \cong (A^\ast \otimes B^\ast)^\ast$. Weakening this condition of compact closed categories yields $\ast$-autonomous categories. From a precausal category $\C$, we construct a category $Caus[\C]$ of higher order causal relations.
### The category of higher order causal processes
Given a set of states $c \subseteq \C(I,A)$ for a system $A$, define its dual by
$$
c^\ast = \{\pi \in A^\ast |\, \forall \rho \in c ,\, \pi \circ \rho = 1\} \subseteq \C(I, A^\ast)
$$
Then we say a set of states $c \subseteq \C(I,A)$ is **closed** if $c=c^{\ast\ast}$, and **flat** if there are invertible scalars $\lambda$, $\mu$ such that $\lambda$  This process is of type $X \otimes C \multimap (A \multimap B) \otimes (B \multimap A) \multimap C'$, where the two middle inputs take types $A \multimap B$ on the left and $B \multimap A$ on the right. Since $\rho'_i \circ \rho_j$ is $1$ if $i=j$ and $0$ otherwise, then plugging in either $\rho_0$ or $\rho_1$ to the bottom left input *switches* the order that the $A \multimap B$ and $B \multimap A$ processes are composed in the final output process. This second order process is causal because
This process is of type $X \otimes C \multimap (A \multimap B) \otimes (B \multimap A) \multimap C'$, where the two middle inputs take types $A \multimap B$ on the left and $B \multimap A$ on the right. Since $\rho'_i \circ \rho_j$ is $1$ if $i=j$ and $0$ otherwise, then plugging in either $\rho_0$ or $\rho_1$ to the bottom left input *switches* the order that the $A \multimap B$ and $B \multimap A$ processes are composed in the final output process. This second order process is causal because
 The authors go on to prove in Theorem 6.17 that a switch cannot be causally ordered, indicating that this process is genuinely second order.
The authors go on to prove in Theorem 6.17 that a switch cannot be causally ordered, indicating that this process is genuinely second order.