Last time in this series we found all the polyhedra that arise in a systematic way from Coxeter diagrams. Before we sail off into new seas, let's review what we've done. To spice things up, I'll explain everything in a different way than before. If you don't see how this new way relates to the old one, please ask! There's a lot to say about this stuff, that I'm not saying. And if you're wondering what that thing is up there, just read on.

Coxeter theory

Harold Scott MacDonald Coxeter, the 'king of geometry', developed a beautiful theory relating group theory to highly symmetrical polyhedra and their higher-dimensional generalizations, called polytopes. His book Regular Polytopes is required reading for anyone who wants to learn about these things. There's a copy sitting by my bed, and there should be one sitting by yours, too. It took him 24 years to write. In his honor, finite groups generated by reflections in n-dimensional space are called Coxeter groups. They're described by diagrams with n dots, called Coxeter diagrams. We've been looking at the 3d case, where there are three such diagrams, with mysterious-sounding names:
A3      o---3---o---3---o
B3      o---3---o---4---o
H3      o---3---o---5---o
I want to show you to use these diagrams. So let's do an example, namely A3:
o---3---o---3---o
This diagram is telling us to draw a bunch of triangles on a sphere, like this:
This shape is called a Coxeter complex. As you can see, it contains lots of great circles. For each one we get a symmetry: a reflection across that circle, as if the circle were the place where a mirror cut our Coxeter complex in half. So, the symmetries of the Coxeter complex form a finite group, generated by reflections. This is a Coxeter group! But how do we get the Coxeter complex from the diagram? The dots in the diagram are secretly called V, E, and F:
V---3---E---3---F
These letters are actually names for the edges of our favorite triangle in the Coxeter complex:
It doesn't matter which is our favorite triangle, so I just picked one. Each edge of this triangle gives a symmetry: the reflection that reflects the Coxeter complex across that edge! We call these symmetries V, E and F. The 3 on the line going between V and E in this diagram:
V---3---E---3---F
is a quick way of saying that
(VE)3 = 1
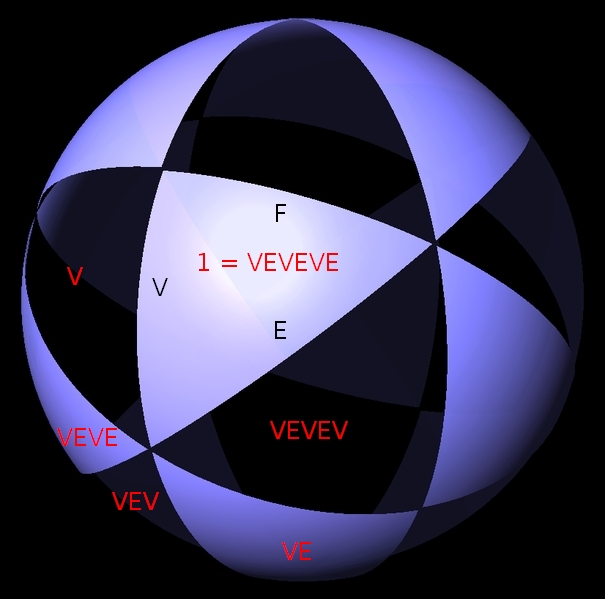
In other words, doing the reflections V, E, V, E, V, E gets us back where we started. To see this, let's call our favorite triangle 1. Reflecting this triangle across the great circle containing the edge V, we get a new triangle, which we'll call V. When we reflect that across the great circle containing the edge E, we get a new triangle, which we'll call VE. And so on:
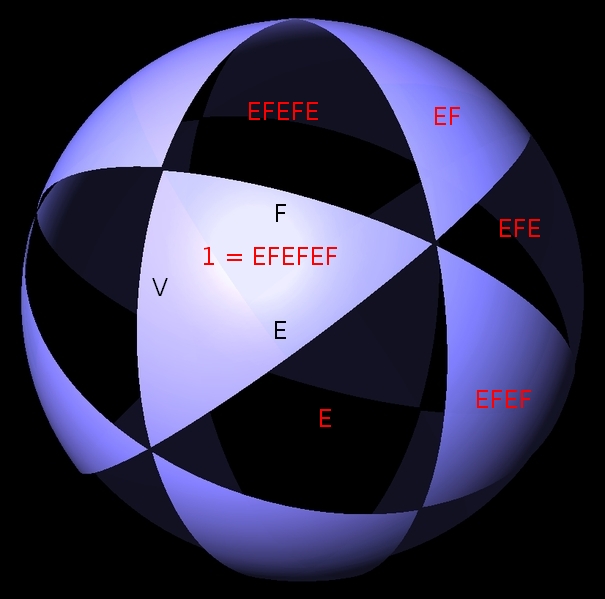
By the time we get to VEVEVE = (VE)3, we're back where we started! That's a total of 6 reflections, so the V and E edges of each triangle must meet at a 60° angle. Similarly, the 3 on the line going between E and V says that
(EF)3 = 1
so doing the reflections E, F, E, F, E, F also gets us back where we started:
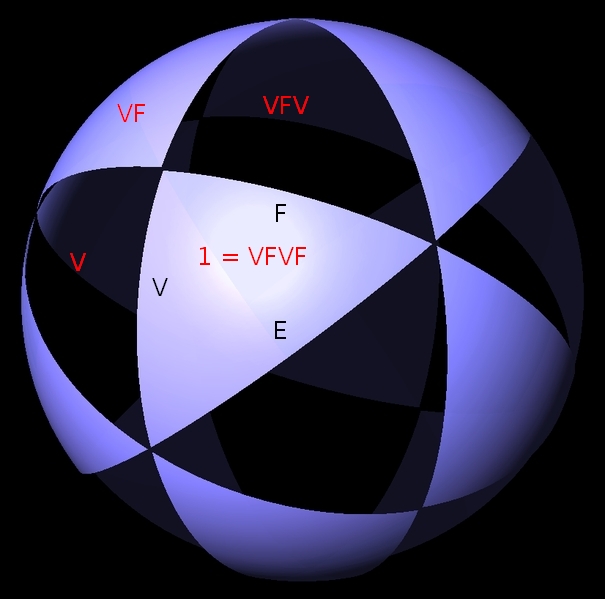
On the other hand, there's no line connecting the dots V and F in our Coxeter diagram:
V---3---E---3---F
But this is short for a line with a 2 on it! You see, this case happens so often that we prefer to save time by not drawing such lines. So, we have
(VF)2 = 1
and doing the reflections V, F, V, F also gets us back where started:
That's a total of 4 reflections, so the V and F edges of each triangle must meet at a 90° angle. So, I've described how the Coxeter group and the Coxeter complex are described by the Coxeter diagram. To be a bit more precise, the Coxeter group A3 has generators V, E, F obeying relations
(VE)3 = (EF)3 = (VF)2 = 1
and also
V2 = E2 = F2 = 1
since V, E, and F are reflections. What makes Coxeter complexes special, compared to other ways of tiling a sphere with triangles? One thing is that they have exactly as many symmetries as triangles. If you pick any triangle and call it your favorite, there's exactly one symmetry—that is, rotation and/or reflection—sending this triangle to any other. So, the Coxeter complex is actually a picture of its own symmetry group! The particular Coxeter complex we've been looking at has 24 triangles. So, its symmetry group has 24 elements. This group is called the tetrahedral finite reflection group, or A3 for short. There's a lot to say about it, but not now! There's another more urgent question.

Polyhedra

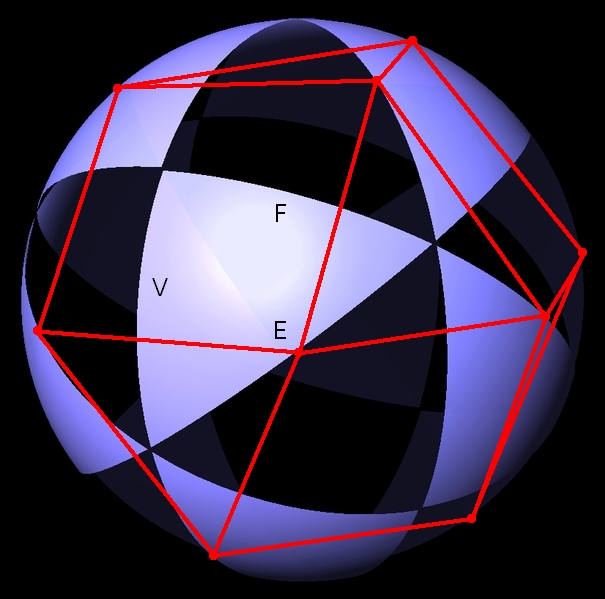
How do we get polyhedra from our Coxeter complex? The easiest one works like this. We take the Coxeter complex and create a polyhedron with a corner in the middle of each triangle, connecting two corners with an edge whenever their triangles touch:
The polyhedron looks better if we view it from a slightly different angle, and let a skilled artist like Tom Ruen do the drawing:
This polyhedron is called the Poincaré dual of the Coxeter complex. There's a notation for this particular polyhedron:
•---3---•---3---•
All the dots are black, because this is the biggest most interesting polyhedron in the A3 family. We get other polyhedra by blackening just some of the dots. In parts 7 and 8, I described how to build these other polyhedra using the concept of 'flag'. But there's another way, using the Coxeter complex, which I'll sketch here. Suppose we blacken just some of the dots in our Coxeter diagram. Then our favorite triangle belongs to a bunch of triangles, all related by reflections corresponding to the dots we left white. And indeed, all the triangles can be grouped into bunches that all look the same... and there's a polyhedron that has a corner in the middle of each bunch of triangles. For example, suppose we leave the E dot white:
•---3---o---3---•
Then our favorite triangle belongs to a bunch of triangles---in this case, just a pair!---that are related by reflections along the E edge of our favorite triangle. If we group our triangles into pairs like this, we get a polyhedron with a corner in the middle of each pair:
Again, it looks better if we let Tom Ruen draw it:
I should do more examples, but I think I'll wrap up by describing the procedure in more highbrow language. Skip the next paragraph if you don't know group theory, and move on to the complete list of examples! If we call the Coxeter group G, blackening all the dots of the Coxeter diagram gives a polyhedron with one corner for each element of G. But if we don't blacken all of them, the reflections corresponding to the white dots generate a subgroup B of G. Then we get a polyhedron with one corner for each element of G/B. Last time I said each way of blackening some dots describes some sort of 'flag', and in these terms, B is the subgroup fixing a flag of this sort, and G/B is the set of flags of this sort. Each of those flags corresponds to what I'm calling a 'bunch of triangles' in my current story. But now let's see what we get from all this! We get three families of polyhedra, and these are almost all the 'Archimedean solids' in 3 dimensions.

The A3 family:     o---3---o---3---o

This family of polyhedra can all be gotten from the tetrahedron by chopping off vertices, edges or faces. They're associated to the Coxeter complex we've just been looking at:
It's built from triangles whose interior angles are $latex \pi/3, \pi/3$ and $latex \pi/2$. These numbers come from taking π and dividing it by the numbers on the edges of the Coxeter diagram: 3, 3, and the invisible edge labelled 2. As mentioned, this Coxeter complex has 24 triangles, and its symmetry group, with 24 elements, is called the tetrahedral finite reflection group, or A3. Here are all the polyhedra in this family. The list has some repeats, because this Coxeter diagram is its own mirror image!
tetrahedron •---3---o---3---o
truncated tetrahedron 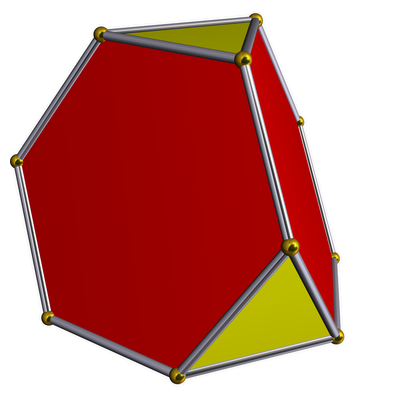•---3---•---3---o
octahedron o---3---•---3---o
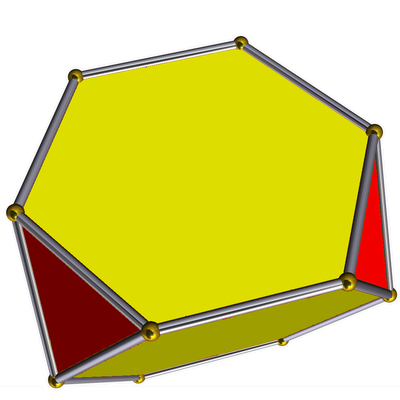
truncated tetrahedron o---3---•---3---•
tetrahedron o---3---o---3---•
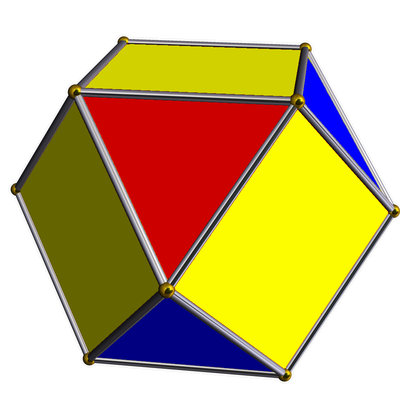
cuboctahedron •---3---o---3---•
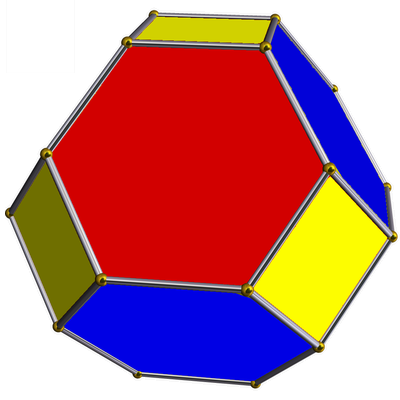
truncated octahedron •---3---•---3---•

The B3 family:     o---3---o---4---o

This family of polyhedra can all be gotten by taking the cube or the octahedron and chopping off vertices, edges or faces. They come from the Coxeter complex whose triangles have interior angles $latex \pi/3, \pi/4$ and $latex \pi/2$:
This Coxeter complex has 48 triangles, and its symmetry group is a Coxeter group with 48 elements, called the octahedral finite reflection group, or B3. Here are all the polyhedra in this family. We've seen some of these already in the A3 family, and there's a reason for that: the group B3 happens to contain A3 as a subgroup! It's twice as big.
cube •---4---o---3---o
truncated cube •---4---•---3---o
cuboctahedron o---4---•---3---o
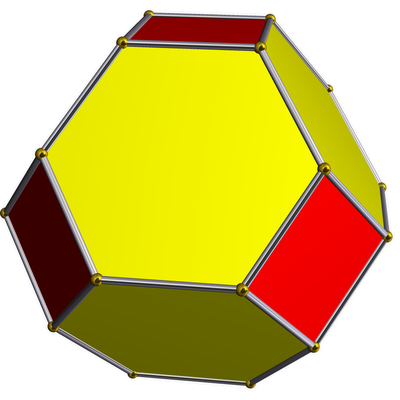
truncated octahedron o---4---•---3---•
octahedron 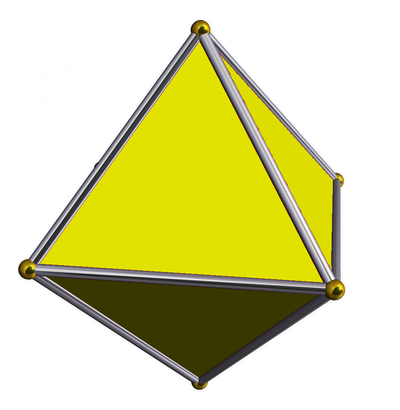o---4---o---3---•
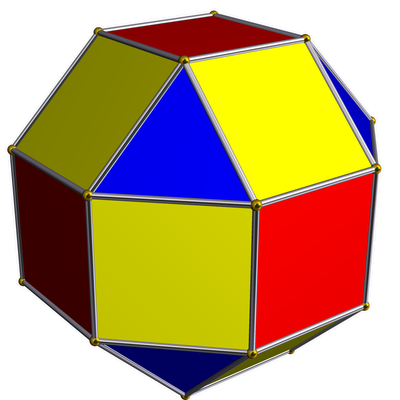
rhombicuboctahedron •---4---o---3---•
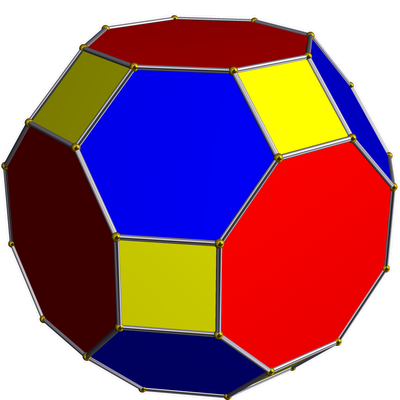
truncated cuboctahedron •---4---•---3---•

The H3 family:     o---3---o---5---o

This family of polyhedra can all be gotten by taking the dodecahedron or icosahedron and chopping off vertices, edges and faces. They come from the Coxeter complex built from triangles whose interior angles are $latex \pi/3, \pi/5$ and $latex \pi/2$:
This Coxeter complex has 120 triangles, and its symmetry group is a Coxeter group with 120 elements, called the icosahedral finite reflection group, or H3. Here are all the polyhedra coming from this Coxeter complex. These are my favorites, because they look the most fancy, and I have a fondness for the quirky charm of 5-fold symmetry:
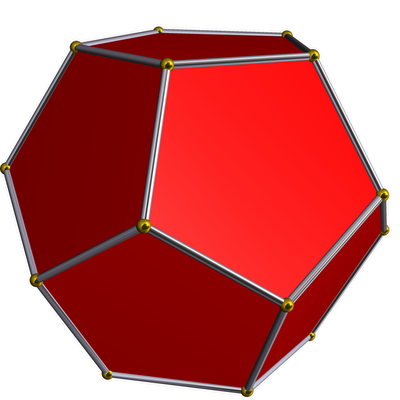
dodecahedron •---5---o---3---o
truncated dodecahedron 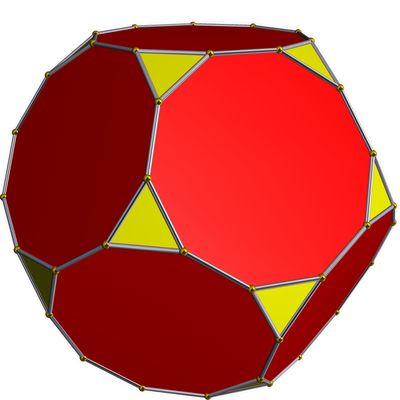•---5---•---3---o
icosidodecahedron 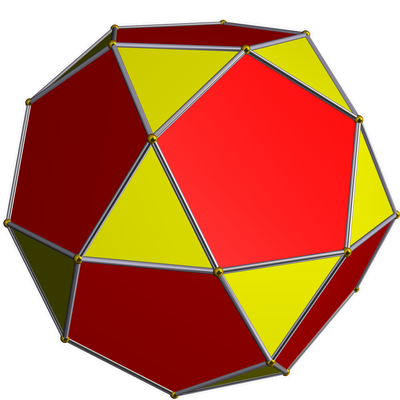o---5---•---3---o
truncated icosahedron o---5---•---3---•
icosahedron o---5---o---3---•
rhombicosidodecahedron •---5---o---3---•
truncated icosidodecahedron •---5---•---3---•

Afterword

The picture at the start of this post was taken by my friend Allen Knutson:
It's the H3 Coxeter complex, and for some reason it's in the library of the music department at Cornell University, where Allen teaches math. The picture of H. S. M. Coxeter is from the cover of a book about him: • King of Infinite Space, ???? As usual, the pretty pictures of solids with brass balls at the vertices were made by Tom Ruen using Robert Webb’s Stella software. Tom Ruen also drew the Coxeter complexes; I'm to blame for the crude labellings added on. You can see the previous episodes of this series here: • Part 1: Platonic solids and Coxeter complexes. • Part 2: Coxeter groups. • Part 3: Coxeter diagrams. • Part 4: duals of Platonic solids. • Part 5: Interpolating between a Platonic solid and its dual, and how to describe this using Coxeter diagrams. Example: the cube/octahedron family. • Part 6: Interpolating between a Platonic solid and its dual. Example: the dodecahedron/icosahedron family. • Part 7: Interpolating between a Platonic solid and its dual. Example: the tetrahedron family. • Part 8: The missing solids, coming from Coxeter diagrams with both ends blackened.