The elliptic curve also has a point at infinity, so its number of points over the field with pn elements is
$$ p^n - \alpha^n - \overline{\alpha}^{\, n} + 1 $$
where \(\alpha \in \mathbb{C}\) has \(|\alpha| = \sqrt{p}\).
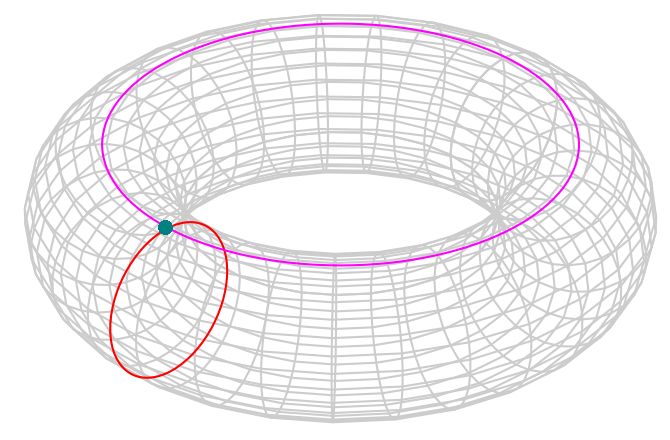
The four terms correspond, in some profound way, to
these four pieces of the elliptic curve over \(\mathbb{C}\), which is a torus:
The pieces of dimension k give the terms that grow
like \(p^{\frac{k}{2} n}\).
