Bibliography

1

J. F. Adams, Lectures on Lie Groups, Benjamin, New York, 1969.

2

J. F. Adams, Lectures on Exceptional Lie Groups, eds. Z. Mahmud and M. Mimira, University of Chicago Press, Chicago, 1996.

3

J. C. Baez, The octonions, Bull. Amer. Math. Soc. 39 (2002), 145-205. Errata in Bull. Amer. Math. Soc. 42 (2005), 213. Corrected version available at math.RA/0105155 or this website.

4

J. W. S. Cassels, An Introduction to the Geometry of Numbers, Springer, Berlin, 1997.

5

J. H. Conway and N. J. A. Sloane, Sphere Packings, Lattices and Groups, 2nd edition, Springer, Berlin, 1993.

6

H. S. M. Coxeter, Integral Cayley numbers, Duke Math. Jour. 13 (1946), 561-578.

7

M. J. Crowe, A History of Vector Analysis, University of Notre Dame Press, Notre Dame, 1967.

8

D. D. Fenster, Leonard Eugene Dickson and his work in the arithmetics of algebras, Arch. Hist. Exact Sci. 52 (1998), 119-159.

9

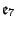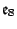Hans Freudenthal, Beziehungen der ${\mathfrak e}_7$ und ${\mathfrak e}_8$ zur Oktavenebene, I, II, Indag. Math. 16 (1954), 218-230, 363-368. III, IV, Indag. Math. 17 (1955), 151-157, 277-285. V -- IX, Indag. Math. 21 (1959), 165-201, 447-474. X, XI, Indag. Math. 25 (1963) 457-487.

10

W. Fulton and J. Harris, Representation Theory -- a First Course, Springer, Berlin, 1991.

11

P. M. Gruber and C. G. Lekkerkerker, Geometry of Numbers, second edition, North-Holland, New York, 1987.

12

M. Gunaydin, K. Koepsell and H. Nicolai, Conformal and quasiconformal realizations of exceptional Lie groups, Comm. Math. Phys. 221 (2001), 57-76. Also available as hep-th/0008063.

13

S. Kaneyuki, Graded Lie algebras, related geometric structures, and pseudo-hermitian symmetric spaces, in Analysis and Geometry on Complex Homogeneous Domains, by Faraut, Kaneyuki, Koranyi, Lu, and Roos, Birkhauser, New York, 2000.

14

T. A. Larsson, Structures preserved by exceptional Lie algebras, available as math-ph/0301006.

15

K. McCrimmon, Jordan algebras and their applications, Bull. Amer. Math. Soc. 84 (1978), 612-627.

16

C. L. Siegel, Lectures on the Geometry of Numbers, Springer, Berlin, 1989.

17

T. A. Springer and F. D. Veldkamp, Octonions, Jordan Algebras and Exceptional Groups, Springer, Berlin, 2000.

18

M. Waldschmidt, P. Moussa, J.-M. Luck, and C. Itzykson, eds., From Number Theory to Physics, Springer, Berlin, 1992.

home