September 3, 2013

Integral Octonions (Part 5)

John Baez

In its full 8-dimensional glory, this shape has:

• 240 vertices
• 6,720 edges
• 60,480 2d faces, which are all equilateral triangles
• 241,920 3d faces, which are all regular tetrahedra
• 483,840 4d faces, which are all regular 4-simplexes
• 483,840 5d faces, which are all regular 5-simplexes
• 207,360 6d faces, which are all regular 6-simplexes
• 19,440 7d faces, consisting of 17,280 regular 7-simplexes and 2,160 regular 7-orthoplexes

and

• a symmetry group with 696,729,600 elements, including rotations and reflections.

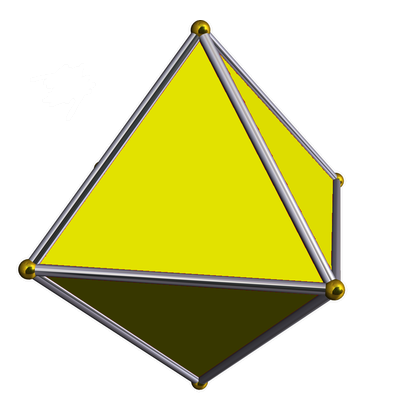
Remember, a 3-simplex is a tetrahedron:

while a 3-orthoplex is an octahedron:

Anyone can look up these crazy numbers on Wikipedia. But how can we see that they're right?

That's our challenge for today. It's easiest if we define the \(\mathrm{E}_8\) root polytope starting from this picture:

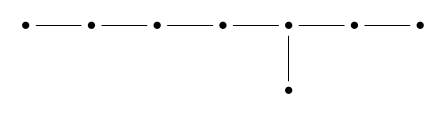
and use the theory of simply-laced Dynkin diagrams, which are Dynkin diagrams without any multiple edges between dots. (Most of what I'm about to say generalizes to other Dynkin diagrams, but I'll save a bit of time by focusing on this case.)

Suppose we've got such a diagram with \(n\) dots. At an elementary level, this diagram tells us to take a bunch of unit vectors in \(n\)-dimensional Euclidean space, and make sure they lie at a \(90^\circ\) angle if there's no edge connecting them, and a \(120^\circ\) angle if there is an edge connecting them.

We get a lattice called the root lattice by taking all integer linear combinations of these vectors. The nonzero vectors closest to the origin are called roots. These roots are the vertices of an \(n\)-dimensional convex polytope called the root polytope.

The roots include the vectors we started with, one for each dot in our Dynkin diagram: these are called the simple roots. But there are also a lot more.

Starting with the \(\mathrm{E}_8\) Dynkin diagram, we can in principle figure out everything we want to know about the \(\mathrm{E}_8\) root polytope, including how many faces of each dimension it has, and the size of its symmetry group. But to do such things elegantly, it helps to use some tricks.

Coxeter groups

The main trick is to use the theory of Coxeter groups. Any simply-laced Dynkin diagram gives such a group, and it's very easy to describe. It has one generator \(s_i\) obeying

for each dot in the Dynkin diagram, one relation

for each pair of dots connected by an edge, and one relation

for each pair of dots not connected by an edge. Each generator \(s_i\) corresponds to a reflection: the reflection that flips the \(i\)th simple root to its negative.

For example, starting with the Dynkin diagram called \(\mathrm{A}_3\):

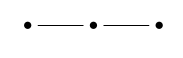
we get a group with 3 generators, which happens to be the symmetry group of a regular tetrahedron:

So, you should think of the three dots in the Dynkin diagram as standing for 'vertex', 'edge' and 'face'. Why? Because the corresponding generators of the Coxeter group are reflections that:

• switch two neighboring vertices,

• switch two neighboring edges, and

• switch two neigboring faces,

respectively!

The \(\mathrm{A}_n\) diagram gives the symmetry group of a regular \(n\)-simplex in just the same way. A similar story applies to the symmetry group of the regular \(n\)-dimensional orthoplex, but the Dynkin diagram for this is not simply laced, so I won't get into the details. The cases we really need now are the \(\mathrm{E}_8\) Dynkin diagram and the sub-diagrams of this.

For example, if we pull off the end dot of \(\mathrm{E}_8\) we get a sub-diagram called \(\mathrm{D}_7\), which looks like this:

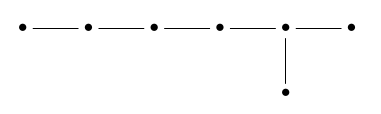
or, after prettying it up, this:

Reading from left to right, can think of the dots here as standing for 'vertex', 'edge', '2d face', '3d face' and so on... but when we get to the right end of the diagram, obviously something funny must happen!

There are two dots that mean 'top-dimensional face'. The reason is that this Coxeter group is the symmetry group of a 7-orthoplex that has its 6-dimensional faces colored alternately white and black. We only consider symmetries that carry faces to faces of the same color. Two 6d faces intersect in at most one 5d face, so there's no dot for '5d face'. We can summarize the story like this:

All the \(\mathrm{D}_n\) Dynkin diagrams look similar, with some number of dots in a row followed by two at the end... and they all work the same way. Their Coxeter groups are the symmetry groups of orthoplexes with their top-dimensional faces colored alternately white and black.

In the case of \(\mathrm{E}_8\), something even stranger happens! The top-dimensional faces are of two kinds: 7-simplex and 7-orthoplex:

Other subtleties arise for the sub-diagrams \(\mathrm{E}_7\) and \(\mathrm{E}_6\). So, you're probably thinking that this subject is an elaborate quagmire. But it's not.

Coxeter complexes

To deal with all Coxeter groups in a systematic way, it's better to think of them as symmetry groups of certain simplicial complexes called 'Coxeter complexes'. Roughly speaking, a simplicial complex is a gadget made of 0-simplexes, 1-simplexes, 2-simplexes, 3-simplexes, and so on — all stuck together in a nice way.

If you have a Coxeter diagram with \(n\) dots, the highest dimension of the simplexes in its Coxeter complex is \(n-1\). There is one of these top-dimensional simplexes for each element of the Coxeter group. For example, I've already said this Dynkin diagram:

gives the Coxeter group consisting of symmetries of a regular tetrahedron — by which I mean all reflections and rotations. This group has 4! = 24 elements, so the Coxeter complex is built from 24 triangles. And in fact, we get it by barycentrically subdividing the surface of a tetrahedron! We can draw it on a sphere, like this:

You can see there are 24 triangles. And, you can see that if you fix a given triangle, there's a unique symmetry of the Coxeter group mapping it to any other triangle.

In general, the Coxeter group of a Dynkin diagram with \(n\) dots always acts as linear transformations of \(\mathbb{R}^n\). Each root gives a reflection that flips that root to its negative. So, this group also acts on the \((n-1)\)-sphere. If we take this sphere and chop it up along the hyperplanes corresponding to all the reflections in the Coxeter group, we get the Coxeter complex. See if you can visualize this in the picture above.

Even better, if you pick any top-dimensional simplex in the Coxeter complex, there always exactly one element of the Coxeter group that maps it to any other top-dimensional simplex. So the Coxeter complex is the best possible thing made out of simplexes on which the Coxeter group acts as symmetries!

The size of the Coxeter group corresponding to a Dynkin diagram is always the product of some integers, one for each dot in the Dynkin diagram. These integers have lots of important properties, and calculating them is really the key to all the problems we've set out to solve. To start with, let me just show you these numbers and what we can do with them.

Here they are. For any Dynkin diagram \(D\), let \(W(D)\) be its Coxeter group, also known as its Weyl group. Here are the sizes of these groups for all the simply-laced Dynkin diagrams:

It's easy to see that \(W(A_n)\), the symmetry group of the \(n\)-dimensional simplex, has size equal to

since the \(n\)-simplex has symmetries permuting its vertices any way you want. While it's not a simply-laced example, it's also easy to see that \(W(B_n)\), the symmetry group of the \(n\)-dimensional orthoplex, has size equal to

This number is equal to the double factorial

Finally, it's also easy to see that \(W(D_n)\), the symmetry group of the orthoplex with its top-dimensional faces colored alternately white and black, is half as big. So, its size is the half double factorial of \(2n\):

So, the only problem is computing the size of \(W(\mathrm{E}_6)\), \(W(\mathrm{E}_7)\), and \(W(\mathrm{E}_8)\). I'll talk about this later.

You might think it's somewhat arbitrary how we wrote the size of these Coxeter groups as products of numbers—but it's not! I'll talk about this more at the end of the article. But here's a little taste of the fun:

Puzzle 1. If you double each of these numbers and subtract one, then add up the results, you get the dimension of the Lie group corresponding to this Dynkin diagram. Why?

Let's check that it works for \(\mathrm{E}_8\):

Yes, this is the dimension of the Lie group \(\mathrm{E}_8\)!

Getting ready to calculate

Assuming we know the size of the Coxeter groups for all the simply-laced Dynkin diagrams, let's see if we can calculate how many faces of each kind the \(\mathrm{E}_8\) root polytope has.

I explained the method in week187. Each Dynkin diagram \(D\) describes a kind of 'incidence geometry' with different kinds of figures—points, edges, triangles, tetrahedra and so on—one for each dot in the Dynkin diagram. These figures can be 'incident' to each other—e.g., a triangle can lie on a tetrahedron—and there's one basic incidence relation for each edge in the Dynkin diagram.

The Coxeter group \(W(D)\) acts transitively on the figures of any given kind. We can also work out the subgroup of \(W(D)\) that preserves a figure of a given kind. To do this, we just remove the corresponding dot from the Dynkin diagram, and get a sub-diagram \(E \subset D\). Then \(W(E) \subseteq W(D)\) is the subgroup we want!

So, the set of the figures of a given kind is \(W(D)/W(E)\). Thus, the number of figures of this kind is the ratio

To see if you understand this, let's do an easy example! How many edges does a tetrahedron have? Here our Dynkin diagram \(D\) is \(\mathrm{A}_3\):

It describes a geometry, namely a tetrahedron, with figures of three kinds:

Suppose we want to count the number of 1-simplexes, or edges. We take the '1-simplex' dot:

and we remove it, obtaining this sub-diagram:

Hmm, this isn't connected! But that's okay. This diagram is the disjoint union of two copies of the one-dot Dynkin diagram, \(\mathrm{A}_1\). If you follow the rules, you'll see its Coxeter group is the product

So, the number of edges in a tetrahedron is

which is right!

If you've never done this sort of stuff, I encourage you to play around with more examples. It's lots of fun! But having spent years warming up with exercises like that, I'm now going to climb Mount Everest and count the various figures in the \(\mathrm{E}_8\) root polytope.

It starts out easy, but near the end, as you might imagine from this picture, it gets tricky—and I'll slip and fall. Hanging from a icy cliff, I'll ask for your help!

0-simplexes

If we remove the 'vertex' dot from the \(\mathrm{E}_8\) Dynkin diagram:

we're left with \(\mathrm{E}_7\)

So, the number of vertices of the \(\mathrm{E}_8\) root polytope is

as we knew!

Just for fun, in the next to last step I cancelled all the numbers I could from the big fraction in the top line. This is worth doing because a \(q\)-deformed version of the same calculation lets us count the number of points in a certain space called a 'Grassmannian' for the version of the group \(\mathrm{E}_8\) defined over the finite field with \(q\) elements, where \(q\) is any prime power. I explained how this works in week186 and week187.

In the \(q\)-deformed count we replace integers with \(q\)-integers, defined as follows:

So, for this particular Grassmannian the number of points is

or, doing all the cancellations we can,

This, believe it or not, is a polynomial in \(q\). But we can't say it's equal to \([240]\), because in general \([n m] \ne [n][m]\). Only when we set \(q = 1\) does this equation hold, and then we get 240 points. So, our problem now, involving Coxeter groups, concerns the special case of the legendary but so far still mythical 'field with one element'.

But if we wanted, we could look at the group \(\mathrm{E}_8\) defined over the field with 2 elements. It acts in a transitive way on a set with

points. How many points is that? In this case

so the number of points is

1-simplexes

If we remove the 'edge' dot from the \(\mathrm{E}_8\) Dynkin diagram:

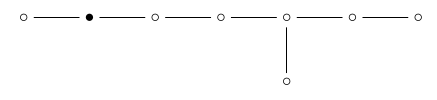
we're left with \( \mathrm{A}_1 \times \mathrm{E}_6\):

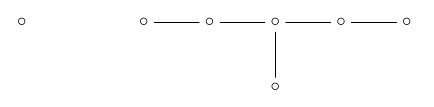
So, the number of edges of the \(\mathrm{E}_8\) root polytope is

2-simplexes

A 2-simplex is just a triangle. If we remove the '2-simplex' dot:

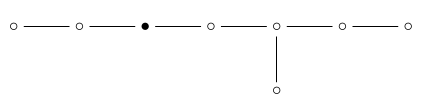
we're left with \(\mathrm{A}_2 \times \mathrm{D}_5\):

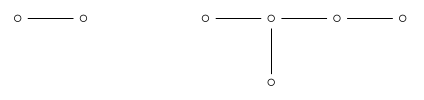
so the number of 2d faces is

3-simplexes

This is a funny picture of a 3-simplex, or tetrahedron. If we remove the '3-simplex' dot:

we're left with \(\mathrm{A}_3 \times \mathrm{A}_4\):

so the number of 3d faces is

4-simplexes

This is a picture of a 4-simplex. If we remove the '4-simplex' dot from the \(\mathrm{E}_8\) Dynkin diagram:

we're left with \(\mathrm{A}_4 \times \mathrm{A}_1 \times \mathrm{A}_2\):

so the number of 4d faces is

5-simplexes

At this point we meet a mystery: there is no '5-simplex' dot in the \(\mathrm{E}_8\) Dynkin diagram!

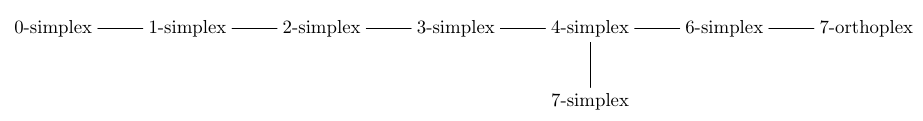
This is a bit like how there is no 5-simplex dot in the \(\mathrm{D}_7\) Dynkin diagram:

The resolution there is that if we have 'complete flag' consisting of one figure of each kind shown in this picture, all incident, there is a unique 5-simplex that's incident to all the other figures. Indeed, there's at most one 5-simplex touching any pair consisting of a white and a black 6-simplex. So, the 5-simplex is 'redundant'.

The same sort of resolution must, I think, apply to \(\mathrm{E}_8\). Figuring this out in detail would make a good test of our understanding. But let's move on!

6-simplexes

If we remove the '6-simplex' dot:

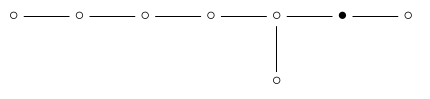
we're left with \(\mathrm{A}_6 \times \mathrm{A}_1\):

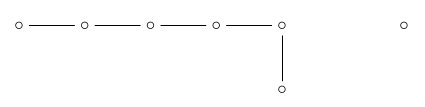
so the number of 6d faces is apparently:

But this does not agree with Wikipedia's answer! It says our polytope has 207,360 6-dimensional faces, which are all regular 6-simplexes. So, we have another mystery on our hands here, which we will return to.

7-simplexes

If we remove the '7-simplex' dot:

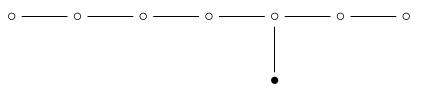
we are left with \(\mathrm{A}_7\):

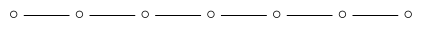
so the number of 7-dimensional simplex faces is:

7-orthoplexes

If we remove the '7-orthoplex' dot:

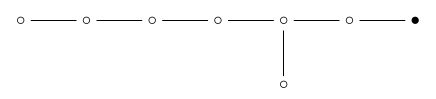
we are left with \(\mathrm{D}_7\):

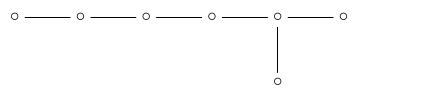
so the number of 7-dimensional orthoplex faces is:

6-simplexes, revisited

First, our calculations seemed to show the number of 6-simplex faces of root polytope of \(\mathrm{E}_8\) is 69,120, while Wikipedia says the answer is 207,360. Luckily we can compute the answer another way, which sheds a little light on this problem.

Our polytope has 17,280 7-simplex faces and 2,160 7-orthoplex faces. Each 7-simplex has 8 faces, all of which are 6-simplexes. Each 7-orthoplex has 2⁷ faces, all of which are 6-simplexes. So, we could naively count the total number of 6-simplexes and get

But this is double-counting, since each 6-simplex touches two 7-simplexes. (The top-dimensional faces of a convex polytope always meet in pairs along faces of the next highest dimension.) So the real count is half this:

This matches the answer on Wikipedia. But it also sheds some light on our wrong answer. Our wrong answer, 69,120, is exactly the total number of faces of all the 7-simplexes. It's also half the total number of faces of the 7-orthoplexes. It's also exactly 1/3 of the correct answer!

All this suggests that the 6-simplex faces of our polytope come in two kinds, which cannot be interchanged by symmetries of the polytope. 1/3 of them are the ones we counted, the kind mentioned in this diagram:

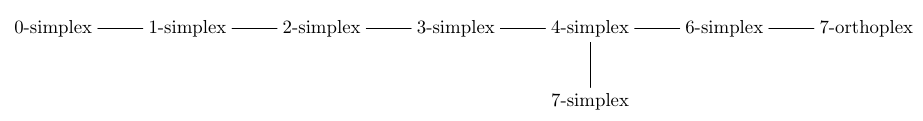
2/3 of them are 6-simplexes of some other kind, which do not appear in the above diagram.

If this seems weird, remember that this diagram also does not include the 5-simplex faces of our polytope! Also remember that the \(\mathrm{D}_7\) diagram, corresponding to the 7-orthoplex, gives another example where some simplexes come in two kinds, while others do not appear at all, even though they exist as faces of the 7-orthoplex:

Even if this is true, it's clearly not enough for a full understanding. If our polytope has two kinds of 6-simplex as faces, how do they differ? And where is the number 1/3 coming from?

Here's my guess. The 7-orthoplex faces of our polytope have 6-simplex faces that can be colored alternately white and black, and all the symmetries of our polytope preserve this two-coloring. As evidence, note that the symmetries preserving a 7-orthoplex form the group \(\mathrm{D}_7\), which preserves such a two-coloring. But I'm guessing we can do this two-coloring in a consistent way, so every 6-simplex in our polytope is either white or black.

And I'm guessing we can do this so that each 7-orthoplex touches another 7-orthoplex on each of its black faces, and a 7-simplex on each of its white faces! On the other hand, every 7-simplex is completely surrounded by 7-orthoplexes.

If we can do this:

• Each white 6-simplex is the face of a unique 7-simplex, so the number of white 6-simplexes is
  $$ 17,280 \cdot 8 = 138,240 $$

  These are the 6-simplexes we counted.

• Each white 6-simplex is the face of a unique 7-orthoplex, so the number of white 6-simplexes is also
  $$ \frac{2,160 \cdot 2^7}{2} = 138,240 $$

  where we get a factor of \(1/2\) because only half the 6-simplex faces of each 7-orthoplex are white. This is a consistency check!

• Each black 6-simplex is the face of two 7-orthoplexes, so the number of black 6-simplexes is
  $$ \frac{2,160 \cdot 2^7}{4} = 69,120 $$
• The total number of 6-simplexes is
  $$ 69,120 + 138,240 = 207,360 $$

  as it says on Wikipedia.

All this fits together nicely... so while I haven't proved the existence of this 'consistent two-coloring' and this arrangement of 6-simplexes and 6-orthoplexes, I believe it.

Puzzle 2. Prove or disprove my guesses here!

5-simplexes, revisited

Why does our polytope have \(483,840\) 5d faces, which are all regular 5-simplexes? I haven't figured out how to count them. With work I should be able to do it using my guesses in the previous section, but I made these guess just a few minutes ago.

Notably, \(483,840\) is also the number of 4d faces.

Puzzle 3. Show how to count the 5d faces of the \(\mathrm{E}_8\) root polytope.

The magic numbers

All my calculations rely on general results that I understand, together with some numbers I don't understand:

In fact for my calculations I only need to know the sizes of these three Coxeter groups, but it's irresistible to try understanding the 'magic numbers' that you can multiply to get their sizes.

Puzzle 4. What's the best way to calculate these magic numbers?

Back in week186 and week187, I gave many characterizations of these numbers. Unfortunately, they don't seem to make it easy to calculate these numbers for \(\mathrm{E}_6, \mathrm{E}_7\) and \(\mathrm{E}_8\).

I bet somebody knows an easy way. But to help you with this puzzle, I'll tell you eight hard ways!

Start with any Dynkin diagram \(D\), not necessarily simply-laced. Let \(G(\mathbb{F})\) be the corresponding simple algebraic group over a field \(\mathbb{F}\). In particular,

is a complex Lie group. Suppose the diagram \(D\) has \(n\) dots. Then the magic numbers \(d_1, \dots, d_n\) are natural numbers such that

Moreover:

1. The real cohomology of \(G\) is an exterior algebra on generators \(x_1, \dots, x_n\), one for each dot of the Dynkin diagram. The degrees of these generators are all odd, and the degree of \(x_i\) is \(2d_i - 1\).
2. The real cohomology of the classifying space \(B G\) is a polynomial algebra on generators \(y_1, \dots, y_n\). The degrees of these generators are all even, and the degree of \(y_i\) is \(2 d_i\).
3. The Weyl group \(W(D)\) acts on \(\mathbb{R}^n\). The algebra of polynomials on \(\mathbb{R}^n\) invariant under this group action is a free commutative algebra on generators \(z_1, \dots, z_n\). The polynomial \(z_i\) is homogeneous of degree \(d_i\).
4. Define the q-polynomial of the Dynkin diagram \(D\) to be the polynomial in \(q\) where the coefficient of \(q^k\) is the number of \(k\)-cells in the Bruhat decomposition of the flag variety \(G/B\). Here \(B\) is the Borel subgroup of \(G\), and the Bruhat decomposition is a standard way of writing \(G/B\) as disjoint union of \(k\)-cells, that is, copies of \(\mathbb{C}^k\). Then the \(q\)-polynomial equals $$ [d_1] \cdot \cdots \cdot [d_n] $$ where \([d_i] = 1 + q + \cdots + q^{d_i}\).
5. If the coefficient of \(q^k\) in the \(q\)-polynomial is \(d\), the \((2i)\)th homology group of \(G/B\) is \(\mathbb{Z}^d.\)
6. The value of the \(q\)-polynomial when \(q\) is a prime power is the cardinality of \(G(\mathbb{F}_q)/B(\mathbb{F}_q)\). Here \(\mathbb{F}_q\) is the field with \(q\) elements, and \(B(\mathbb{F}_q)\) is the Borel subgroup of the simple algebraic group \(G(\mathbb{F}_q)\).
7. The coefficient of \(q^k\) in the \(q\)-polynomial is the number of Coxeter group elements of length \(k\). Here the length of any element in the Coxeter group is its minimal length as a word when we write it as product of the generators \(s_1, \dots, s_n\) corresponding to dots in the Dynkin diagram.
8. The coefficient of \(q^k\) in the polynomial is the number of top-dimensional simplexes of distance \(k\) from a chosen top-dimensional simplex in the Coxeter complex. Here we measure 'distance' between top-dimensional simplexes in the hopefully obvious way, based on how many walls you need to cross to get from one to the other.

If you know enough stuff you may have fun proving all these descriptions of the magic numbers are equivalent.

I have not managed to use any of these descriptions of the magic numbers to solve this problem:

Puzzle 5. Why is these sequence of magic numbers for any Dynkin diagram 'symmetrical'?

To explain what I mean here, look at the pattern of spacings between magic numbers for \(\mathrm{E}_6\):

It doesn't change when you reflect it! The same is true for \(\mathrm{E}_7, \mathrm{E}_8\) and also the non-exceptional cases if you write the magic numbers in increasing order. Why? It's reminiscent of Poincaré duality, but I don't see how it is that.

Puzzle 1. If you double each of the magic numbers and subtract one, then add up the results, you get the dimension of the Lie group corresponding to this Dynkin diagram. Why?

Answer. A self-contained proof can be found in Humphrey's book Reflection Groups and Coxeter Groups; see Theorem 3.9. Personally I prefer using the fact that the real cohomology of the Lie group \(G\) corresponding to the Dynkin diagram is an exterior algebra on generators \(x_i\) of degrees \(2d_i - 1\). Thus, the highest-degree element in the cohomology of \(G\) is the product \(x_1 \cdots x_n\), which has degree \( \sum_{i=1}^n (2d_i - 1) \). But the highest degree possible in the cohomology of \(G\) is just the dimension of \(G\).

Puzzle 2. Show that the faces of the 7-orthoplexes in the \(\mathrm{E}_8\) polytope can be 2-colored in an alternating way so that their black faces touch other 7-orthoplexes, while their white faces touch 7-simplexes.

Answer. Layra Idrani answered:

You can prove the black-white thing by example, or at least I did.

Letting our vertices be

$$ (\pm 1,\pm 1,0,0,0,0,0,0) $$

and permutations, and

$$ (\pm 1/2,\pm 1/2,\pm 1/2,\pm 1/2,\pm 1/2,\pm 1/2,\pm 1/2,\pm 1/2) $$

with an even number of \(-1/2\)s, we get that a pair of vertices are connected by an edge iff their inner product is 1.

We can look at the following orthoplex:

$$(1,1,0,0,0,0,0,0) $$ $$ (1,0,1,0,0,0,0,0) $$ $$ (1,0,0,1,0,0,0,0) $$ $$ (1,0,0,0,1,0,0,0) $$ $$ (1,0,0,0,0,1,0,0) $$ $$(1,0,0,0,0,0,1,0) $$ $$ (1,0,0,0,0,0,0,1) $$ $$ (1,-1,0,0,0,0,0,0) $$ $$ (1,0,-1,0,0,0,0,0) $$ $$ (1,0,0,-1,0,0,0,0) $$ $$ (1,0,0,0,-1,0,0,0) $$ $$ (1,0,0,0,0,-1,0,0) $$ $$ (1,0,0,0,0,0,-1,0) $$ $$ (1,0,0,0,0,0,0,-1) $$

Now we figure out which sets of seven can be extended to a simplex via adding another vertex.

Consider a vertex \((1,-1,0,0,0,0,0,0)\). For another vertex to have an edge to it, i.e. to have inner product 1, its first entry must be positive or 0, and its second entry must be negative or 0, since otherwise there would be a negative term in the inner product; both entries can't be 0, and if both are non-zero then they must be 1/2 and -1/2 respectively.

Similarly, for any other vertex \(v\) in the orthoplex, any vertex \(w\) connected to \(v\) must either match the sign of \(v\) in precisely one of the two non-zero entries of \(v\), or \(w\) must match both and all of its coordinates must have magnitude 1/2. We take a set of seven vertices in our orthoplex such that except for the first entry, if \(v\) has a non-zero entry somewhere then the other 6 vertices have 0 there. These are all our 6-dimensional simplices in our orthoplex, since any other set would contain a pair of vertices whose inner product is 0. Suppose that of these, \( \{v_i\}\) for \(i\) from 1 to \(k\) each have a -1 in position \(i\). The point that has coordinate -1/2 in position \(i\) and 1/2 in all other positions is of distance 2 from all the vertices given. Such a point is a vertex iff \(k\) is even. So that gives us 64 6-simplices that extend to 7-simplices. Moreover, these 6-simplices alternate with the remaining 6-simplices, since given a 6-simplex with an even number of vertices that have a -1 in them, changing any of the vertices such that we still get a 6-simplex in the orthoplex yields a 6-simplex with an odd number of vertices with a -1 in them, and vice versa.

Now we just need to show that the other 64 6-simplices don't extend to 7-simplices. Consider a set of seven vertices in the orthoplex such that an odd number have an entry of -1 and the seven vertices form a 6-simplex.

Suppose we have a vertex \(w\) with a 0 entry. If it has 1 as its first entry, then it must have an entry of 1 or -1 somewhere else, and thus either matches or is orthogonal to a vertex in our 6-simplex. If \(w\) has 0 as its first entry, then it must have non-zero entries in two other places, but as there are then five remaining entries, there is a vertex in our 6-simplex that is 0 in those two places and hence is orthogonal to \(w\). If \(w\) has only entries of \(\pm 1/2\), then it must match each vertex in our simplex wherever that simplex is non-zero, but doing so yields a point with an odd number of entries of -1/2, which is not a vertex. So these 6-simplices cannot be extended to 7-simplices, and hence must be connected to orthoplexes (orthoplices?).

So this particular orthoplex has precisely half of its 6-faces connected to simplices, and the other half to other orthoplexes, and such faces alternate. By symmetry, this applies to all the orthoplexes.

Puzzle 3. Show how to count the 5d faces of the \(\mathrm{E}_8\) root polytope.

Answer. Layra Idrani give an explanation of the answer in Wikipedia:

In terms of the 5-simplices, the fastest way I can think to do it is to count the number of 5-simplices per 7-simplex (28) and then multiply by the number of 7-simplices (17280). This gives the right answer (483,840). Now we just have to show that this is the correct calculation to do.

We know that we only have to worry about 5-simplices that are contained in 7-simplices, since for any 5-simplex in an orthoplex, it can extend to a white 6-simplex, and uniquely so.

To show that each 5-simplex is in a unique 7-simplex, we look at 4-simplices. According to the diagram, each 4-simplex A is contained in exactly two 7-simplices, denoted B and C. Hence if a 5-simplex D contains A, then it can only be contained in B or C, no other 7-simplices, and indeed must be contained in at least one of B or C. Since all 5-simplices are identical, if any 5-simplex is in two 7-simplices, each 5-simplex must be in two 7-simplices.

So we assume that D is in both B and C. Since any other D' that contains A must be in B or C, and D is in two simplices, D' must also be in both B and C. We know that D' exists since B has more than one vertex that isn't in A.

D and D' share 5 vertices and are both in the same 7-simplex B, and so thus together define a unique 6-simplex, and that 6-simplex is contained in B. But by assumption, they're also both in C, and so that same 6-simplex is also in C. Thus we get that B and C share a 6-simplex, which is impossible.

Hence D is in exactly one of B and C, and similarly every 5-simplex is in precisely one 7-simplex.

The only part of this answer I didn't undertand is why every 4-simplex lies in exactly two 7-simplexes. However, I was able to confirm this using a slight extension of the technique already used in this article.

First I'll count the pairs consisting of a 4-simplex and a 7-simplex that contains it. Then I'll count the 4-simplexes. Then I'll divide the first number by the second and get 2.

To count the pairs consisting of a 4-simplex and a 7-simplex that contains it, I mark those dots in the Dynkin diagram:

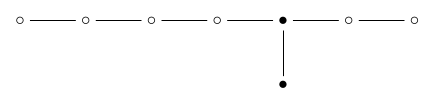
and then remove them:

leaving me with the Dynkin diagram for \(\mathrm{A}_4 \times \mathrm{A}_2\). So, the number of these pairs is $$ \begin{array}{ccl} \frac{|W(\mathrm{E}_8)|}{|W(\mathrm{A}_4)| \times |W(\mathrm{A}_2)| \times |W(\mathrm{A}_4)|} &=& \frac{2 \cdot 8 \cdot 12 \cdot 14 \cdot 18 \cdot 20 \cdot 24 \cdot 30}{(2 \cdot 3 \cdot 4 \cdot 5) \times (2 \times 3)}\end{array} $$ On the other hand, I already counted the number of 4-simplexes. But just as a reminder: to do this, we remove just the 4-simplex dot from the Dynkin diagram:

leaving us with \(\mathrm{A}_4 \times \mathrm{A}_1 \times \mathrm{A}_2\):

so the number of 4d faces is $$ \begin{array}{ccl} \frac{|W(\mathrm{E}_8)|}{|W(\mathrm{A}_4)| \times |W(\mathrm{A}_1)| \times |W(\mathrm{A}_4)|} &=& \frac{2 \cdot 8 \cdot 12 \cdot 14 \cdot 18 \cdot 20 \cdot 24 \cdot 30}{(2 \cdot 3 \cdot 4 \cdot 5) \times 2 \times (2 \cdot 3)} \end{array} $$ You can see this is half our previous answer. So, yes: there are two 7-simplexes containing each 4-simplex!

Puzzle 4. What's the best way to calculate the magic numbers for a given Dynkin diagram?

Proposition 3.20. If \(h\) is the Coxeter number of the Dynkin diagram \(D\) and \(1 \le m \le h\) is relatively prime to \(h\), then \(m+1\) is a magic number for \(D\).

Recall that the Coxeter number is the number of roots divided by the number of dots in the Dynkin diagram. (For other more conceptual descriptions, click the link!)

To use this proposition, it may help to know that the number of roots is the dimension of the Lie algebra corresponding to \(D\) minus the number of dots in \(D\). For example, the dimension of the Lie algebra \(\mathrm{E}_8\) is 248, and its Dynkin diagram has 8 dots, so the number of roots is \(248 - 8 = 240\) (which we already knew), and its Coxeter number is \(240/8 = 30\). The numbers between 1 and 30 that are relatively prime to 30 are: $$ 1, 7, 11, 13, 17, 19, 23, 29 $$

So, adding one, we get some magic numbers for \(\mathrm{E}_8\):

But there are eight of them, and there's always just one magic number for each dot in the Dynkin diagram, so these must be all the magic numbers!

This is black magic, and even the normally imperturbable Humphreys gives it an exclamation mark.

By the way, did you notice something funny about these numbers:

Except for 1, they're all prime! 30 just happens to be the largest number for which every number besides 1 that's smaller than it and relatively prime to it is actually prime. I don't know if this is important here, but it's darn suspicious.

For \(\mathrm{E}_7\) we have to work harder. The dimension of the Lie algebra \(\mathrm{E}_7\) is 133, so the number of roots is \(133 - 7 = 126\), and the Coxeter number is \(126/7 = 18\). Here are the numbers smaller than 18 that are relatively prime to 18: $$ 1, 5, 7, 11, 13, 17 $$ Adding one, we get magic numbers for \(\mathrm{E}_7\): $$ 2, 6, 8, 12, 14, 18 $$ Unfortunately we only get six of the seven magic numbers this way. Luckily, Humphreys also proved that the sequence of magic numbers must be 'symmetrical' as described in Puzzle 5. The only possibility is that the seventh magic number is 10: $$ \begin{array}{ccccccccccccccccc} 2 &&&& 6 &&8 && \mathbf{10} && 12 &&14 &&&& 18 \\ \bullet &\circ &\circ &\circ & \bullet &\circ &\bullet &\circ &\bullet &\circ &\bullet &\circ &\bullet &\circ&\circ &\circ& \bullet \end{array} $$ By the way, did you notice anything funny about these numbers: $$ 1, 5, 7, 11, 13, 17 ?$$

Yes, again they're all prime. Like 30, 18 is a very round number, meaning that every nature number relatively prime to it and smaller than it is either 1 or prime.

For \(\mathrm{E}_6\) we must work even harder for our supper, but I'll leave that as a puzzle for you! To get you started, I'll remind you that the dimension of the \(\mathrm{E}_6\) is 78, so the number of roots is \(78 - 6 = 72\), so the Coxeter number is \(72/6 = 12\). Also: puzzle 1 may come in handy.

(By the way, the only very round numbers are $$ 1, 2, 3, 4, 6, 8, 12, 18, 24, 30 $$ and it is a mystery to me that three of them have come up in this discussion. But it is easy to see that there's no very round number bigger than \(30\). First, it would have to be divisible by \(2, 3\), and \(5\), or else some product of two of these primes would be relatively prime to this number and smaller than it, but not prime. So the first option is \(60\). \(60\) is not very round because \(7^2\) is relatively prime to it but not prime. In short, the problem is that there's a prime that does not divide \(60\) whose square is less than \(60\). So, any round number bigger than \(30\) actually needs to be divisible by \(7\), too, which means it must be bigger than \(2 \times 3 \times 5 \times 7 = 210\). But \(11^2 < 210\) and \(13^2 < 210\), so any round number bigger than \(30\) must actually be bigger than \(2 \times 3 \times 5 \times 7 \times 11 \times 13\). And so on: this is clearly a losing battle. At this stage, knowing there's always a prime between \(n\) and \(2n\) is enough to guarantee that we can keep up this argument by induction.)

The second method for computing magic numbers is more systematic.

This method uses the concept of the height of a positive root, meaning the sum of its coefficients when expanded as a linear combination of simple roots. To calculate the magic numbers, you calculate how many positive roots of each height there are, and use this to get a partition of the total number of positive roots. For example, \(\mathrm{B}_2\) has 2 positive roots of height one, 1 of height two and 1 of height three, so we get the partition (2,1,1).

Then you write this partition as a Young diagram:

XX
X
X

XXX
X

This sounds insane, but it's true! It's Theorem 3.20 in Humphreys' book — the last theorem in the book.

Puzzle 5. Why is the sequence of magic numbers for any Dynkin diagram 'symmetrical'?

Allen is correct; this symmetry is Lemma 3.16 in Humphreys. The quick explanation is that \(\zeta^{d_i-1}\) for \(\zeta\) a particular \(h\)-th root of unity is the set of eigenvalues of the Coxeter element. Since this is a real matrix, its eigenvalues come in complex conjugate pairs. Here \(h\) is the Coxeter number, the order of the Coxeter element.

© 2013 John Baez
baez@math.removethis.ucr.andthis.edu
home