Bibliography

1

S. Abramsky and B. Coecke, A categorical semantics of quantum protocols, available at http://www.arXiv.org/abs/quant-ph/0402130.

2

M. F. Atiyah, Topological quantum field theories, Publ. Math. IHES Paris 68 (1989), 175-186.

M. F. Atiyah, The Geometry and Physics of Knots, Cambridge U. Press, Cambridge, 1990.

3

J. Baez, Bell's inequality for C*-algebras, Lett. Math. Phys. 13 (1987), 135-136.

4

J. Baez, Spin foam models, Class. Quantum Grav. 15 (1998), 1827-1858. Also available at http://www.arXiv.org/abs/gr-qc/9709052.

J. Baez, An introduction to spin foam models of quantum gravity and BF theory, in Geometry and Quantum Physics, eds. H. Gausterer and H. Grosse, Springer, Berlin, 2000, pp. 25-93. Also available at http://www.arXiv.org/abs/gr-qc/9905087.

5

J. Baez, Higher-dimensional algebra and Planck-scale physics, in Physics Meets Philosophy at the Planck Length, eds. Craig Callender and Nick Huggett, Cambridge U. Press, Cambridge, 2001, pp. 177-195. Also available at http://www.arXiv.org/abs/gr-qc/9902017 and this website.

6

J. Baez and J. Dolan, Higher-dimensional algebra and topological quantum field theory, Jour. Math. Phys. 36 (1995), 6073-6105. Also available at http://www.arXiv.org/q-alg/9503002.

7

M. Barr and C. Wells, Toposes, Triples and Theories, Springer Verlag, Berlin, 1983. Revised and corrected version available at http://www.cwru.edu/artsci/math/wells/pub/ttt.html.

8

J. S. Bell, On the Einstein-Podolsky-Rosen paradox, Physics 1 (1964), 195-200.

9

A. Boileau, A. Joyal, La logique des topos, J. Symb. Logic 46 (1981), 6-16.

10

D. Corfield, Towards a Philosophy of Real Mathematics, Cambridge U. Press, Cambridge, 2003.

11

M. Coste, Langage interne d'un topos, Seminaire Bénabou, Université Paris-Nord 1972.

12

R. L. Crole, Categories for Types, Cambridge U. Press, Cambridge, 1993.

13

A. Arageorgis, J. Earman, and L. Ruetsche, Weyling the time away: the non-unitary implementability of quantum field dynamics on curved spacetime, Studies in the History and Philosophy of Modern Physics, 33 (2002), 151-184.

14

A. Einstein, B. Podolsky, and N. Rosen, Can quantum-mechanical description of physical reality be considered complete?, Phys. Rev. 47 (1935) 77.

15

E. Hawkins, F. Markopoulou and H. Sahlmann, Evolution in quantum causal histories, Class. Quant. Grav. 20 (2003), 3839-3854. Also available at http://www.arXiv.org/abs/hep-th/0302111.

16

P. Johnstone, Toposes as theories, in Sketches of an Elephant: A Topos Theory Compendium, vol. 2, Oxford U. Press, Oxford, 2002, pp. 805-1088.

17

A. Kanamori, The empty set, the singleton, and the ordered pair, Bull. Symb. Logic 9 (2003), 273-298. Also available as http://www.math.ucla.edu/~asl/bsl/0903/0903-001.ps.

18

J. Lambek, From 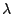$\lambda$-calculus to cartesian closed categories, in To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, eds. J. P. Seldin and J. R. Hindley, Academic Press, New York, 1980, pp. 375-402.

19

G. Lakoff and R. Núñez, Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being, Basic Books, 2000.

20

J. Lambek and P. J. Scott, Introduction to Higher-Order Categorical Logic, Cambridge U. Press, Cambridge, 1986.

21

F. W. Lawvere, Functorial Semantics of Algebraic Theories, Ph.D. Dissertation, Columbia University, 1963.

22

J.-L. Loday, J. Stasheff and A. Voronov, eds., Operads: Proceedings of Renaissance Conferences, American Mathematical Society, Providence, Rhode Island, 1997.

23

S. Mac Lane, Natural associativity and commutativity, Rice Univ. Stud. 49 (1963) 28-46.

24

S. Mac Lane and I. Moerdijk, Sheaves in Geometry and Logic: a First Introduction to Topos Theory, Springer Verlag, Berlin, 1992.

25

M. Markl, S. Shnider and J. Stasheff, Operads in Algebra, Topology and Physics, American Mathematical Society, Providence, Rhode Island, 2002.

26

L. Mauri, Algebraic theories in monoidal categories, available at http://www.math.rutgers.edu/~mauri.

27

C. McLarty, Elementary Categories, Elementary Toposes, Clarendon Press, Oxford, 1995.

28

W. Mitchell, Boolean topoi and the theory of sets, J. Pure Appl. Alg. 2 (1972), 261-274.

29

G. Segal, The definition of a conformal field theory, in Topology, Geometry and Quantum Field Theory: Proceedings of the 2002 Oxford Symposium in Honour of the 60th Birthday of Graeme Segal, ed. U. L. Tillmann, Cambridge U. Press, 2004.

30

L. Smolin, Three Roads to Quantum Gravity, Basic Books, New York, 2001.

L. Smolin, How far are we from the theory of quantum gravity?, available at http://www.arXiv.org/abs/hep-th/0303185.

31

R. Vaas, The duel: strings versus loops, trans. M. Bojowald and A. Sen, available at http://www.arXiv.org/abs/physics/0403112.

32

W. K. Wootters and W. H. Zurek, A single quantum cannot be cloned, Nature 299 (1982), 802-803.

© 2004 John Baez
baez@math.removethis.ucr.andthis.edu

home