Selection Rules Redux

We start in a stationary state $v(0)$. We wait a bit. Under the influence of the electromagnetic perturbation $V$, $v$ evolves to a state which is a superposition of $v(0)$ and other stationary states $u_j$. What can we say about the possible $u_j$?

At first you might guess that one could not say anything without a detailed study of $V$. Say $\{u_j\}$ is a basis of eigenvectors of $H$. Expand $v(t)$ out in this basis:

$$v(t) = \sum_j c_j(t) u_j$$

It turns out that for small positive $t$, $c_j(t)\approx 0$ unless $Vv(0)$ contains a non-zero $u_j$ component. Say we set $v(0)=u_i$, and expand out $Vu_i$ in the $\{u_j\}$ basis-- $Vu_i=\sum_j a_{ij}u_j$. We must have $a_{ij}\neq 0$ to have a significant chance of the transition $u_i \rightarrow u_j$.

Let's rephrase this without so many indices. $V$ has a matrix representation in the basis of eigenvectors of $H$. ``Immediate'' transitions between ``stationary states'' (i.e., eigenvectors of $H$) come from non-zero off-diagonal entries in the $V$ matrix.

Over longer periods of time, we can have transitions through intermediate states: $u_i \rightarrow u_j \rightarrow u_k$. If you work through the math, you will find out that you are computing $V^2$, $V^3$, etc., for these indirect transitions; the power series for $\exp(iV)$ makes an appearance in the final result.

The moral of this tale is that zero entries in the $V$ matrix correspond to forbidden transitions. A selection rule translates into an assertion about the form of the $V$ matrix. And so, it appears, we need a detailed study of $V$ to determine the selection rules.

Our crude ``derivation'' of the selection rules for $S$ indeed depended on the ``mechanism'' of light. But for $J$, we appealed to a general physical principle, conservation of angular momentum. Can one not translate this argument into quantum mechanics?

One can. The thread runs thus: $V$ must be invariant under all spatial rotations, for electromagnetism does not single out any preferred direction in space. So the group of spatial rotations, $SO(3)$, must play a special role. At this point group representation theory takes over, and out pops the selection rules for $J$ and $M_J$. (You do need some additional assumptions I won't spell out.)

Let's take a last look at the Paschen-Back effect, using all we've learned. Where do the $J,M_J$ selection rules leave off and the $L,M_L$ and $S,M_S$ selection rules take over, as we increase the magnetic field?

Both sets of selection rules hold throughout! The trick is picking the right basis. To understand this, we must consider again the combined influence of the spin-orbit and magnetic perturbations.

The operator $H$ looks like this:

$$H = H^0 + c_1 {\bf L}\cdot{\bf S} + c_2 {\bf B}\cdot({\bf L}+2{\bf S})$$

or equally well:

$$H = H^0 + c_1 {\bf L}\cdot{\bf S} + c_2 {\bf B}\cdot({\bf J}+{\bf S})$$

$H^0$ contains terms representing the attraction of the nucleus, and perhaps other refinements for complex atoms. The next two terms are the spin-orbit coupling and the effect of the magnetic field.

B is just a conventional 3-space vector, but L, S, and J are all ``operator vectors''. That is, for any coordinate system, we have ${\bf L}=(L_x,L_y,L_z)$, where $L_x$, $L_y$, and $L_z$ are all operators. Ditto for S and J.

Pick the $z$-axis in the direction of the magnetic field. Several operators now demand a role:

$$\begin{eqnarray*} {\bf J}\cdot{\bf J} &=& J_xJ_x+J_yJ_y+J_zJ_z\\ {\bf L}\cdot{\... ...{\bf L}\cdot{\bf S} &=& L_xS_x+L_yS_y+L_zS_z\\ J_z,&L_z,&S_z\\ \end{eqnarray*}$$

some with eigenvalues we've come to know and love:

$$\begin{eqnarray*} {\bf J}\cdot{\bf J}& \rightarrow & J(J+1)\\ {\bf L}\cdot{\bf ... ...tarrow& M_J\\ L_z &\rightarrow& M_L\\ S_z &\rightarrow& M_S\\ \end{eqnarray*}$$

Alas, these operators do not all commute. It turns out that ${\bf L}\cdot{\bf L}$ and ${\bf S}\cdot{\bf S}$ commute with each other and all the rest, and hence with $H$. For this reason, $L$ and $S$ are ``good'' quantum numbers: we can pick stationary states (in the Bohr sense) that have sharp values for $L$ and $S$.

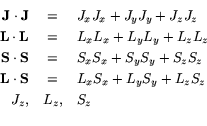
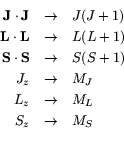
Finding additional ``good'' quantum numbers proves more frustrating. ${\bf J}\cdot{\bf J}$ commutes with $J_z$ and with ${\bf L}\cdot{\bf S}$, but not with $L_z$ or $S_z$ (as it happens). Drop the ${\bf B}\cdot{\bf S}$ term from $H$, and we have $J$ and $M_J$ as good quantum numbers. Alternately, drop the spin-orbit coupling term, and, as luck will have it, $M_L$ and $M_S$ become good quantum numbers.

So we have a choice of bases. With no field, we can find stationary states with sharp values of $(L,S,J,M_J)$. With no spin-orbit coupling, we can demand sharp values for $(L,S,M_L,M_S)$.

Start with the $(L,S,J,M_J)$ basis, and turn on a weak field. The states are now only approximately stationary (even in Bohr's sense). The stronger the field, the less accurate the approximation. But the matrix elements for $V$, in this basis, strictly obey the $J$ and $M_J$ selection rules, no matter how strong the field.

For a very strong field, the $(L,S,M_L,M_S)$ basis consists of approximately stationary states (i.e., near-eigenvectors of $H$). The $M_L$ and $M_S$ selection rules hold strictly with respect to this basis, no matter how weak the field. (The $L$ and $S$ selection rules hold for either basis.)

Just to hose away the last traces of the muddle: how can we reconcile $\Delta M_S = 0$ with the formulas $M_S=g(J,L,S)M_J$ and $\Delta M_J = 0, \pm 1$? (We needed the latter two formulas for the anomalous Zeeman effect.) Answer: Suppose an atom makes a transition from $\vert M_J=\uparrow\rangle$ to $\vert M_J=\downarrow\rangle$ (using the Dirac $\vert\rangle$ notation for state-vectors, plus the ``colloquial'' abbreviations $\uparrow=\frac{1}{2}$, $\downarrow=-\frac{1}{2}$). The atom begins and ends in an eigenstate of $J_z$. Each eigenstate is a ``blend'' of eigenstates of $S_z$, say:

$$\begin{eqnarray*} \vert M_J=\uparrow\rangle &=& a\,\vert M_S=\uparrow\rangle + ... ...\,\vert M_S=\uparrow\rangle + d\,\vert M_S=\downarrow\rangle\\ \end{eqnarray*}$$

The selection rule for $M_S$ holds, in the sense that $\vert M_S=\uparrow\rangle$ makes a transition only to itself; likewise for $\vert M_S=\downarrow\rangle$. But the coefficients $a$, $b$, $c$, and $d$ change. The $M_S$ in the equation $M_S=g(J,L,S)M_J$ is an ``average'' $M_S$, and depends on these coefficients. (More precisely, it is the expectation value of $S_z$ for a state which is an eigenstate of $J_z$, not of $S_z$.) The $M_S$ of the selection rule is the quantum number of an eigenstate of $S_z$.

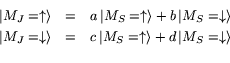
We have already seen this resolution foreshadowed in the classical treatment, when we obtained the ``average'' $z$-component of S by taking the $z$-component of ${\bf S}_\parallel$. But classical mechanics lacks the notion of ``blended'' states, and so is ill-equipped to pass smoothly from the weak field to the strong field regime.

So much for the Zeeman effect. Let us punctuate the tale with an anecdote. A friend ran into Heisenberg on the streets of Cophenhagen, around 1920; Heisenberg had a grim expression. ``Cheer up, Werner, things can't be that bad!'' Replied Heisenberg, ``How can one be cheerful when one is thinking about the anomalous Zeeman effect?''

© 2001 Michael Weiss

home