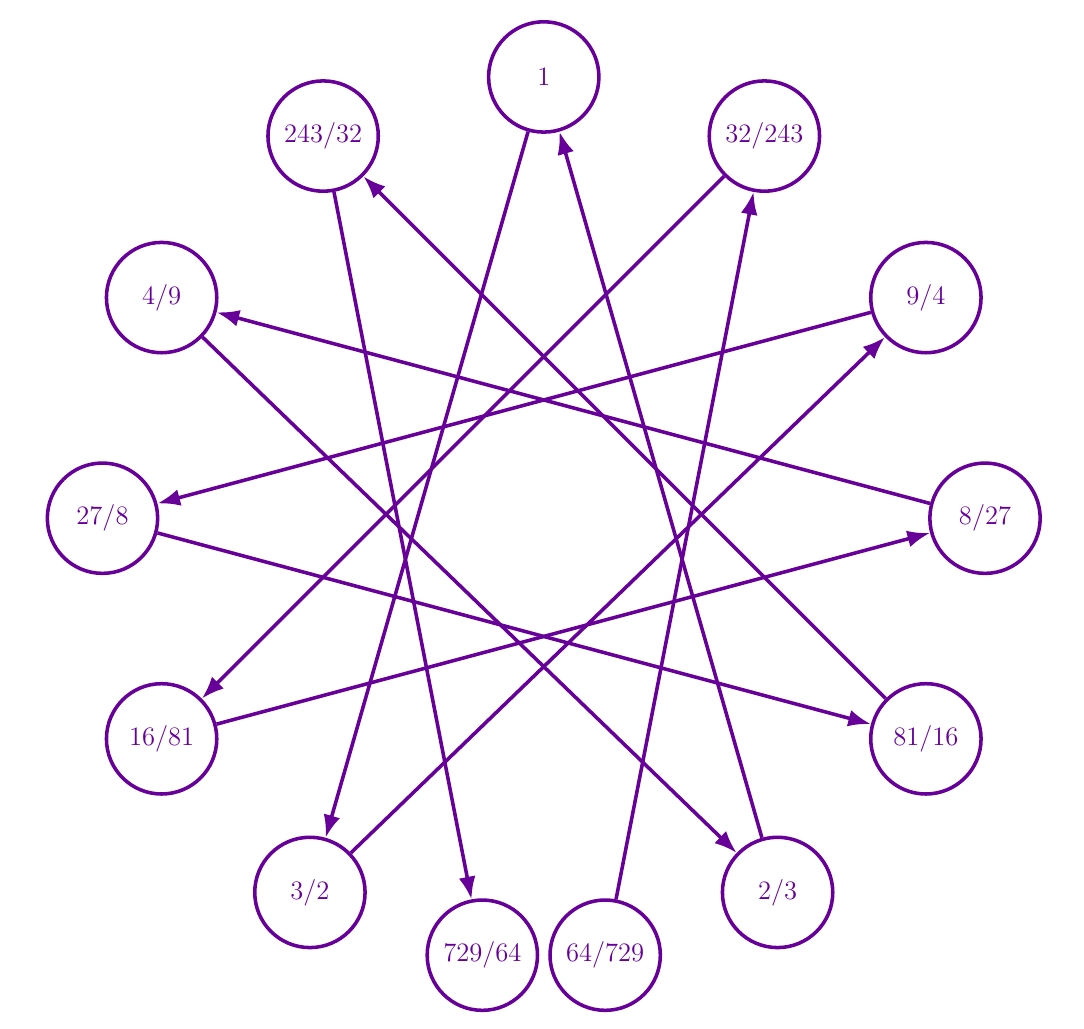
An important early tuning system is Pythagorean tuning, where we force all frequency ratios to involve only powers of 2 and 3. In music, 3/2 is the 'fifth’: the most consonant of intervals except for the octave.
If we start with some frequency and go up and down by powers of 3/2, we create the 'circle of fifths’ shown above. It's almost a 12-pointed star, with one point for each note in the 12-tone equal-tempered scale.
Almost — but not quite! When we go up 12 fifths, we get a tone that's almost but not quite 2 times the frequency we started with. In other words, it's almost but not quite 7 octaves higher. So there's a glitch.
Here I've stuck that glitch at the opposite from the pitch labeled 1. That's a good place for it, because the spot directly opposite 1 is called the 'tritone’, or sometimes diabolus in musica: the 'devil in music’.
Let me explain the chart a bit more carefully. I started with any pitch and arbitrarily called its frequency 1. Then I climbed up 6 fifths, multiplying the frequency by 3/2 each time, getting pitches with frequencies
$$ 1, 3/2, 9/4, 27/8, 81/16, 243/32, 729/64 $$
Going all the way around the circle clockwise means going up an octave: that is, multiplying the frequency by 2. So each time I multiplied the frequency by 3/2, I went log2(3/2) of the way clockwise around the circle: that is, about 0.585 of the way around, a bit more than half-way.
Then I climbed down 6 fifths, going counterclockwise and dividing the frequency by 3/2 each time, getting pitches with frequencies
$$ 1, 2/3, 4/9, 8/27, 16/81, 32/243, 64/729 $$
These are the reciprocals of the numbers we saw going up.
Why did I stop when I did? 729/64 is nowhere close to 64/729, but their ratio is almost a power of 2:
$$ \displaystyle{ \frac{729/64}{64/729} = \left(\frac{3}{2}\right)^{12} \! \approx 129.7 } $$
while
$$ \displaystyle{ 2^7 = 128 } $$
So our star is close to a 12-pointed star. But there's a glitch. And the size of the glitch is called the Pythagorean comma:
$$ \displaystyle{ \frac{(3/2)^{12}}{2^7} = \frac{3^{12}}{2^{19}} \approx 1.01364326477 } $$
This is one of the problems afflicting Pythagorean tuning, and later I'll say a bit about how people deal with it.
Now let's multiply the frequencies we've seen by powers of 2 to make them lie between 1 and 2. That gives us a scale that lies within a single octave:
These different pitches have names, by the way! Not just in Pythagorean tuning but in other related tuning systems, like the equal-tempered scale widely used in music today. Here they are: with their frequencies in the Pythagorean system: $$ \def\arraystretch{1.4} \begin{array}{lc} \textbf{tonic} & 1 \\ \textbf{minor 2nd} & \frac{256}{243} \\ \textbf{major 2nd} & \frac{9}{8} \\ \textbf{minor 3rd} & \frac{32}{27} \\ \textbf{major 3rd} & \frac{81}{64} \\ \textbf{major 4th} & \frac{4}{3} \\ \textbf{diminished 5th} & \frac{1024}{729} \\ \textbf{augmented 4th} & \frac{729}{512} \\ \textbf{perfect 5th} & \frac{3}{2} \\ \textbf{minor 6th} & \frac{128}{81} \\ \textbf{major 6th} & \frac{27}{16} \\ \textbf{minor 7th} & \frac{16}{9} \\ \textbf{major 7th} & \frac{243}{128} \\ \textbf{octave} & 2 \\ \end{array} $$
In the equal-tempered scale there's no difference between the augmented 4th and the diminished 5th: they're both the tritone. But in Pythagorean tuning they're different. And surprisingly, the augmented 4th is higher in pitch than the diminished 5th.
It may or may not help you to see the abbreviations for these different pitch names:
I could talk about this chart all day, but most of what I'd say would apply just as well to the equal-tempered scale. The big difference is that in Pythagorean tuning, unlike the equal-tempered scale, the augmented 4th (A4) and diminished fifth (d5) are not the same note. They are very close: the chart is not to scale, and if it were these two pitches would be almost on top of each other. But they're not the same!
It also may or may not help you to see the names for these pitches when the frequency we arbitrarily called 1 is the note called C:
We get a funny version of the scale with 13 notes, because F sharp (the augmented 4th in the key of C) is different from G flat (the diminished 5th).
Okay, but what if we want a scale with just 12 notes? We usually remove the diminished 5th, and make the augmented 4th do whatever jobs the diminished 5th would have done! So, we change our chart to this:
Or, in terms of frequencies, this:
This looks terrible, but more importantly it creates a badly out-of-tune pair of notes, namely those connected by the new red edge. These pitches have an ugly frequency ratio of
$$ \displaystyle{ \frac{729/512}{256/243} = \frac{3^{11}}{2^{17}} \approx 1.351524} $$
If we hadn't used the augmented 4th for a job the diminished 5th should be doing, we'd have gotten the much nicer-sounding ratio
$$\displaystyle{ \frac{1024/729}{256/243} = \frac{4}{3} \approx 1.333333} $$
The difference is audible and unpleasant: we've created what's called a 'wolf interval’, called that because it howls like a wolf. Unsurprisingly, the ugly ratio divided by the nicer ratio is our old nemesis, the Pythagorean comma:
$$\displaystyle{ \frac{3^{11}/2^{17}}{4/3} = \frac{3^{12}}{2^{19}} \approx 1.01364326477 } $$
It's interesting to look at the frequency ratios of neighboring notes in the Pythagorean scale: $$ \def\arraystretch{1.4} \begin{array}{lcccc} \textbf{minor 2nd / tonic} \phantom{ABC} & \frac{256}{243}\big/1 &=& 256/243 \\ \textbf{major 2nd / minor 2nd} & \frac{9}{8}\big/\frac{256}{243} &=& 2187/2048 \\ \textbf{minor 3rd / major 2nd} & \frac{32}{27}\big/\frac{9}{8} &=& 256/243 \\ \textbf{major 3rd / minor 3rd} & \frac{81}{64}\big/\frac{32}{27} &=& 2187/2048\\ \textbf{major 4th /major 3rd} & \frac{4}{3}\big/\frac{81}{64} &=& 256/243 \\ \textbf{augmented 4th / major 4th} & \frac{729}{512}\big/\frac{4}{3} &=& 2187/2048 \\ \textbf{perfect 5th / augmented 4th} & \frac{3}{2}\big/\frac{729}{512} &=& 256/243 \\ \textbf{minor 6th / perfect 5th} & \frac{128}{81}\big/\frac{3}{2} &=& 256/243 \\ \textbf{major 6th / minor 6th} & \frac{27}{16}\big/\frac{128}{81} &=& 2187/2048 \\ \textbf{minor 7th / major 6th} & \frac{16}{9}\big/\frac{27}{16} &=& 256/243 \\ \textbf{major 7th / minor 7th} & \frac{243}{128}\big/\frac{16}{9} &=& 2187/2043 \\ \textbf{octave / major 7th} & 2\big/\frac{243}{128} &=& 256/243 \\ \end{array} $$
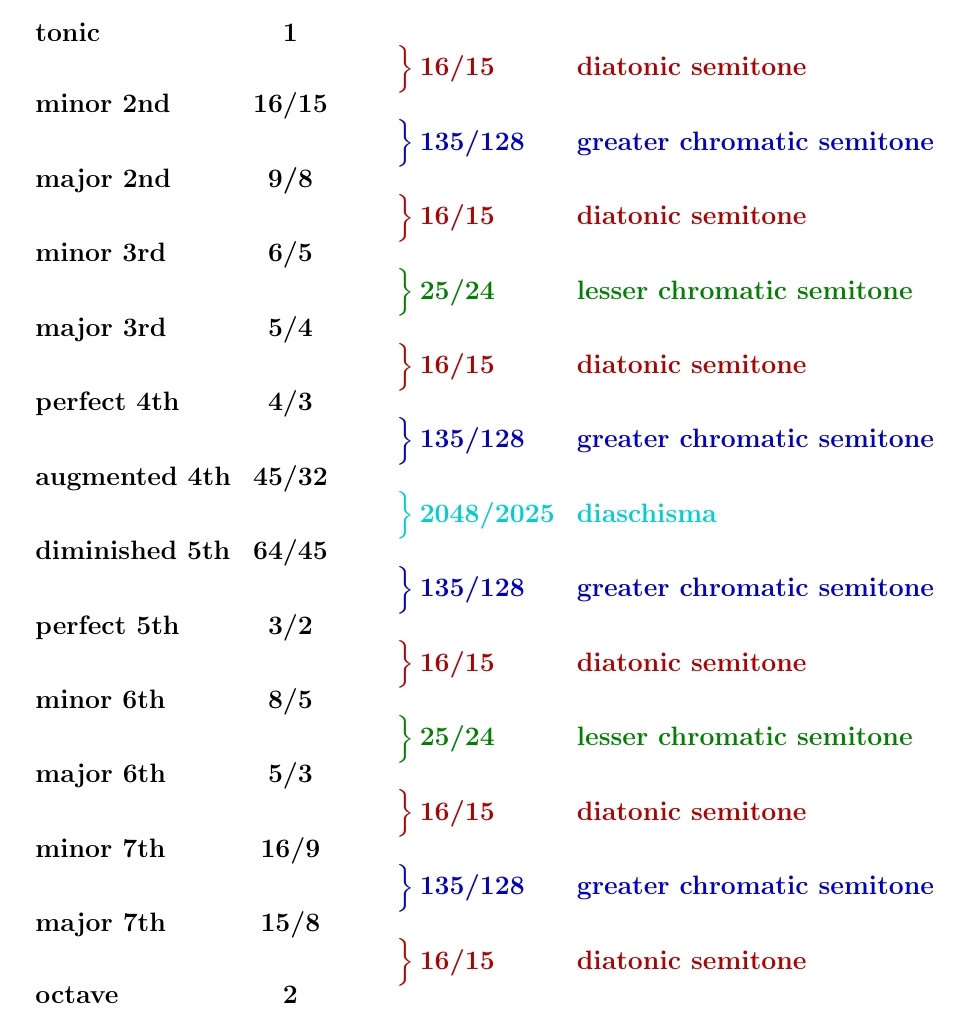
In the equal-tempered scale the frequency ratio of neighboring notes is always 21/12, and it's called a semitone. But as you can see, in the Pythagorean scale some neighboring notes have a frequency ratio of 256/243, while others have a ratio of 2187/2048. So there are two kinds of semitones in the Pythagorean scale:
The Pythagorean chromatic semitone is bigger than the Pythagorean diatonic semitone. How much bigger? What's their ratio?
$$\displaystyle{ \frac{2187/2048}{256/243} = \frac{3^{12}}{2^{19}} \approx 1.01364326477 } $$
Yes, it's the Pythagorean comma! Like a bad penny, it keeps coming back to haunt us.
By the way, the word 'limma' is from a Greek word meaning 'remnant', and it's used for several small intervals in music. The word 'apotome' is from a Greek word meaning 'cutting off', and it's apparently used only for this particular interval, as well as other things in mathematics and optics.
The somewhat irregular pattern of semitones in my chart above would become symmetrical if we had kept the diminished 5th, but then there would be a Pythagorean comma between the augmented 4th and diminished 5th, like this: $$ \def\arraystretch{1.4} \begin{array}{lcccc} \textbf{minor 2nd / tonic} \phantom{ABC} & \frac{256}{243}\big/1 &=& 256/243 \\ \textbf{major 2nd / minor 2nd} & \frac{9}{8}\big/\frac{256}{243} &=& 2187/2048 \\ \textbf{minor 3rd / major 2nd} & \frac{32}{27}\big/\frac{9}{8} &=& 256/243 \\ \textbf{major 3rd / minor 3rd} & \frac{81}{64}\big/\frac{32}{27} &=& 2187/2048\\ \textbf{major 4th / major 3rd} & \frac{4}{3}\big/\frac{81}{64} &=& 256/243 \\ \textbf{diminished 5th / major 4th} & \frac{1024}{729}\big/\frac{4}{3} &=& 256/243 \\ \textbf{augmented 4th / diminished 5th} & \frac{729}{512}\big/\frac{1024}{729} &=& 531441/524288 \\ \textbf{perfect 5th / augmented 4th} & \frac{3}{2}\big/\frac{729}{512} &=& 256/243 \\ \textbf{minor 6th / perfect 5th} & \frac{128}{81}\big/\frac{3}{2} &=& 256/243 \\ \textbf{major 6th / minor 6th} & \frac{27}{16}\big/\frac{128}{81} &=& 2187/2048 \\ \textbf{minor 7th / major 6th} & \frac{16}{9}\big/\frac{27}{16} &=& 256/243 \\ \textbf{major 7th/minor 7th} & \frac{243}{128}\big/\frac{16}{9} &=& 2187/2043 \\ \textbf{octave / major 7th} & 2\big/\frac{243}{128} &=& 256/243 \\ \end{array} $$
Now the chart is symmetrical from top to bottom. The big nasty fraction in the middle is the Pythagorean comma:
$$\displaystyle{ \frac{531441}{524288} = \frac{3^{12}}{2^{19}} \approx 1.01364326477 }$$
Besides the Pythagorean comma — and the wolf interval we get if we try to avoid it — another big problem with Pythagorean tuning is that some very important intervals are represented by fairly complicated fractions. The ear seems to enjoy simple fractions! There are other tuning systems that do better at this, like 'just intonation’. For example, in Pythagorean tuning the minor third is 32/27 above the tonic, while in just intonation it's 6/5. In Pythagorean tuning the major third is a ridiculous 81/64 above the tonic, while in just intonation it's 5/4. Arguably just intonation gets these things right, while Pythagorean tuning gets them wrong.
I hope to write more about just intonation later! To finish off, here's a comparison between Pythagorean tuning and equal temperament:
I'm not trying to imply that equal temperament is 'correct', but at right I'm showing the Pythagorean frequency divided by the corresponding equal-tempered frequency. It's a bit remarkable how close they are! The biggest deviations occur for the augmented 4th and diminished 5th, which are the same in equal temperament but separated by a comma in the Pythagorean scale. The second biggest deviations occur for the minor 2nd and major 7th. All these are fairly dissonant intervals even in the best of worlds. But the third biggest occur for the major 3rd and minor 6th.
Here's a picture comparing Pythagorean tuning and equal temperament:
Equal-tempered is black and Pythagorean is green. You can see the diminished fifth and augmented fourth straddling the tritone.
So much more to say! But I'll quit here for now.
Equal Temperament (Part 1)
In my October 8th entry I explained how Pythagorean tuning, one of the older tuning systems, arises from the fact that twelve fifths is almost the same as seven octaves. In other words, multiplying by 3/2 twelve times is almost the same as multiplying by 2 seven times: \[ \displaystyle{ \left(\frac{3}{2}\right)^{12} \! \approx 129.7 > 128 = 2^7 } \]
But not quite! That's why the star above does not quite close.
In the most widely used modern scale, we deal with this discrepancy by using a fifth that does not have a frequency ratio of 3/2, but rather
\[ \displaystyle{ 2^{7/12} \approx 1.49830707688} \]
It's a bit off, but not much. So it sounds pretty good, and most of us have decided to accept it (though I love those of you who haven't). We then equally divide this fifth into 7 steps, each with a frequency ratio of 21/12. We thus divide the octave into 12 steps, each with a frequency ratio of 21/12. The result is called the equal-tempered 12-tone scale, or 12-TET for short.
The only question I want to discuss today is: why 12 tones? What if we tried an equal-tempered scale with some other number of tones?
The historical question of how Western music arrived at a 12-tone scale is complicated. It seems much of the evidence is lost in the mists of time. I'm not qualified to tackle this question. Indeed, nothing I've read so far has convinced me that anyone is qualified, though I want to read more. So instead I'll just talk about the math.
Furthermore, I'll take a very narrow view of the question! When choosing a tuning system there are many factors at work. At the very least, for each interval you might like to play, you should ask how well a given tuning system accommodates that interval. In common practice Western music this includes asking how all the major thirds and fifths sound in a given tuning system — since major triads, consisting of a tone, the major third above that tone, and the perfect fifth above that tone, are so fundamental to this music. It's generally thought that a really nice major triad has frequency ratios
\[ 1 : \frac{5}{4} : \frac{3}{2} \]
And so, mathematically, we can take any tuning system and ask how closely its major triads come to having these frequency ratios. For example, in just intonation we make some major triads have exactly these frequency ratios... while others are quite bad.
But because I've recently been thinking about Pythagorean tuning, which is about fifths, in this entry I won't talk about major thirds at all — much less the myriads of other issues — and focus with laser-like single-mindedness on the question of fifths in equal-tempered scales. I hope to talk about other things later.
Clearly \[ \displaystyle{ 2^{7/12} \approx 1.49830707688} \] is remarkably close to 3/2. How well could we approximate the frequency ratio 3/2 if we used an equal-tempered scale with some other number of tones?
For a scale with n tones, this amounts to finding the power of 21/n that comes closest to 3/2. Here's how it works:
\[ \begin{array}{llllcl} \textbf{1-TET} & 2^{1/1} & = & 2.00000 &\; \; & 33.3333\% \\ \textbf{2-TET} & 2^{1/2} & \approx & 1.41421 &\; \; & -5.7191\% \\ & 2^{2/3} & \approx & 1.58740 && +5.8267\% \\ & 2^{2/4} & \approx & 1.41421 && -5.7191\% \\ \textbf{5-TET} & 2^{3/5} & \approx & 1.51572 && +1.1048\% \\ & 2^{4/6} & \approx & 1.58740 && +5.8267\% \\ \textbf{7-TET} & 2^{4/7} & \approx & 1.48599 && -0.9337\% \\ & 2^{5/8} & \approx & 1.54221 && +2.8141\% \\ & 2^{5/9} & \approx & 1.46973 && -2.0177\% \\ & 2^{6/10} & \approx & 1.51572 && +1.1048\% \\ & 2^{6/11} & \approx & 1.45948 && -2.7013\% \\ \textbf{12-TET} & 2^{7/12} & \approx & 1.49831 && -0.1129\% \\ \\ \textbf{29-TET} & 2^{17/29} & \approx & 1.50129 && +0.08629\% \\ \textbf{41-TET} & 2^{24/41} & \approx & 1.50042 && +0.02796\% \\ \textbf{53-TET} & 2^{31/53} & \approx & 1.49994 && +0.00394\% \\ \end{array} \]
At right I show the percentage error of the approximate fifth: for example, 21/2 is 5.7191% less than 3/2. The rows with names have a better perfect fifth than any row above. After 12-TET I got tired of showing you every row, and just showed the scales whose perfect fifth beats all previous scales.
◆ 1-TET is a ridiculous scale that only lets you play octaves, so its best approximate fifth is the octave.
◆ 2-TET also has a terrible approximate fifth: it's 21/2, the tritone, which is extremely dissonant.
◆ 5-TET is surprisingly good for a scale with so few tones, with an approximate fifth just 1.1048% too high. Many different pentatonic scales are used worldwide, but the pentatonic scale called slendro in Javanese and Balinese gamelan music is pretty close to 5-TET.
◆ 7-TET has an approximate fifth that's 0.9337% too low, just a bit better than 5-TET. Oddly I'm having trouble finding examples of music in 7-TET. Apparently it was used in some traditional Chinese music. I'd love to know more details.
◆ Then comes 12-TET, a marked improvement with a fifth that's just 0.1129% too low.
It's impossible not to notice that 5 + 7 = 12, and that our standard use of 12-TET on a piano divides the 12 tones into 5 black keys and 7 white keys.
The black keys form a pentatonic scale, while the white keys form the so-called diatonic scale. Both are widely used in Western music — and in the case of the diatonic scale that's a massive understatement: see my article on modes of the major scale for some ways it's used.
These pentatonic and diatonic scales are significantly different from 5-TET and 7-TET, since their notes are not close to evenly spaced. And yet I can't help but wonder if some faint shadow of 5-TET and 7-TET hangs over 12-TET, and the way we subdivide it into pentatonic and diatonic scales.
Mathematically, it seems to be a sheer coincidence that 5-TET, 7-TET and 12-TET give particularly good fifths and 5 + 7 = 12. But later I'll mention a few more facts that make this fact even more tantalizing!
◆ 29-TET is the next winner: its fifth is just 0.08629% too high. It has been argued that in 1318 the medieval Italian music theorist Marchetto da Padova proposed a system that is approximately 29-TET:
I'll admit I'm not convinced.
◆ 41-TET has a fifth that's just 0.02796% too high. This has been used or at least studied enough to have its own Wikipedia page:
The pianist and engineer Paul von Janko built a piano using this tuning, which is on display at the Gemeentemuseum in the Hague. I recommend looking at the Wikipedia page to see how much more detailed it is than anything I'm saying here. Then look at this:
and see what true devotion looks like! Xenharmonic music is music that uses tuning systems other than 12-TET.
◆ 53-TET is a massive improvement, with a fifth that's only 0.00394% too high, so this scale has been on people's radar for a long time. Wikipedia again has an article on it:
and this time the historical section is interesting enough to quote in detail:
Theoretical interest in this division goes back to antiquity. Jing Fang (78–37 BCE), a Chinese music theorist, observed that a series of 53 just fifths (3⁄253) is very nearly equal to 31 octaves (231). He calculated this difference with six-digit accuracy to be 177147⁄176776. Later the same observation was made by the mathematician and music theorist Nicholas Mercator (c. 1620–1687), who calculated this value precisely as
\[ \displaystyle{ \frac{3^{53}}{2^{84}} = \frac{19383245667680019896796723}{19342813113834066795298816} }\]which is known as Mercator's comma. Mercator's comma has a small value to begin with (≈ 3.615 cents), but 53 equal temperament flattens each fifth by only 1⁄53 of that comma (≈ 0.0682 cent ≈ 1⁄315 syntonic comma ≈ 1⁄344 Pythagorean comma). Thus, 53 tone equal temperament is for all practical purposes equivalent to an extended Pythagorean tuning.
After Mercator, William Holder published a treatise in 1694 which pointed out that 53 equal temperament also very closely approximates the just major third (to within 1.4 cents), and consequently 53 equal temperament accommodates the intervals of 5 limit just intonation very well. This property of 53-TET may have been known earlier; Isaac Newton's unpublished manuscripts suggest that he had been aware of it as early as 1664–1665.
Mercator's observation that 53-TET has a good approximate 'just major third' boils down to the fact that
\[ \displaystyle{ 2^{17/53} \approx 1.24898 }\]
is close to 5/4 = 1.25.
I find all the history here fascinating. Nicholas Mercator is not the guy with the Mercator projection — that was Gerardus Mercator. He's the guy who invented the term 'natural logarithm' and discovered that \[ \displaystyle{ \ln(1 + x) = 1 + x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots }\]
By the way, 'Mercator' just means 'merchant', and Nicholas Mercator's German name was 'Kauffman'. I hope sometime to say more about the work of Mercator and Newton on tuning systems.
By the way, remember my observation that three good scales 5-TET, 7-TET and 12-TET are related by 5 + 7 = 12? After I posted this article, Sylvain pointed out on Mastodon that 29-TET, 41-TET and 53-TET are related by similar formulas! \[ \begin{array}{ccl} 29 &=& 12+12+5 \\ 41 &=& 12+12+12+5 \\ 53 &=& 12+12+12+12+5 \end{array} \]
More coincidences? Or is something deeper at work here? I have no idea!
What's next? Is there a systematic way to get ahold of these equal-tempered scales with good approximate fifths?
Yes: the key is to study the number
since this number x has
so if we find a good rational approximation to x, say
then we get
so in an equal-tempered scale with q tones, the fifth will be close to p tones above the octave.
To find good rational approximations to x we can take its continued fraction expansion... I'll do it using Wolfram Alpha... and get
If we truncate this at some point we get a good rational approximation to x and thus an equal-tempered scale with a good approximate fifth. For example \[ \displaystyle{ \frac{1}{1 + \frac{1}{1 + \frac{1}{2 + \frac{1}{2}}}} = \frac{7}{12} } \]
This says that 12-TET has a pretty good approximate fifth, and we get it by going up 7 steps on this 12-tone scale.
If we do this systematically we get these rational approximations to x:
1
1/2
3/5
7/12
24/41
31/53
179/306
389/665
9126/15601
18641/31867
46408/79335
65049/111202
111457/190537
6195184/10590737
6306641/10781274
31421748/53715833
100571885/171928773
131993633/225644606
and so on. I thank Chris Grossack for showing me how to compute these using Sage.
This list includes all the 'best so far' equal-tempered scales on my previous list except for 7-TET. It skips straight from 5-TET to 12-TET. Why is that — what's the underlying math here? I imagine there's quite a bit to say, not about this one particular case but about the general theory of approximating numbers by rationals. I know continued fractions give good results, but what about all the other 'best so far' approximations: that is, rational approximations that are better than any with a smaller denominator? Are they common, rare, etc.?
We can also get new scales, using \[ \begin{array}{ccl} 2^{179/306} & \approx & 1.50000501098 \\ 2^{389/665} & \approx & 1.49999990153 \\ 2^{9126/15601} & \approx & 1.50000000175 \\ 2^{18641/31867} & \approx & 1.49999999966 \end{array} \]
and so on.
Of course, this is basically an argument for why you shouldn't let mathematicians get involved with tuning systems. A scale with 306 or more tones is not very practical — and even though we can compose and play music on such scales using computers, the ear will not greatly prefer the fifths in this scale to those in 53-TET.
To be frank, most people are perfectly happy with 12-TET! And I should lay my cards on the table: my overall goal is not to find better tuning systems, but to better understand the math behind the historically most important 12-tone tuning systems. I would like to write about these:
These dates are very rough, and I'd love to find some books that
investigate the history more carefully... but anyway, I'm not sure
I'll even get around to discussing all these systems. But I'd like
to! There is some mildly fancy math that could be brought in, which I
haven't seen people using.
Equal Temperament (Part 2)
When I listed some equal-tempered scales with good perfect fifths (see
my October 15th entry, a
reader named Sylvain
noticed something interesting. The scales with 5, 7, 12, 17, 29, 41
and 53 tones are particularly good, and
17 = 12 + 5
29 = 12 + 12 + 5
41 = 12 + 12 + 12 + 5
53 = 12 + 12 + 12 + 12 + 5
I asked if this is a coincidence. And now I know the answer: no, it's not! There really is a reason for this pattern.
As we'll see, part of the reason is that $$ 7/12 \approx 0.58333333333... $$ is very close to $$ \log(3/2)/\log(2) \approx 0.58496250072... $$ But we'll also see it's crucial that 5 × 7 is slightly less than a multiple of 12. As far as I can tell, these coincidences are unrelated.
Surprisingly, the further coincidence that 5 + 7 = 12 seems to play no role here. But of course there are 5 black notes and 7 white notes in the scale on a piano, and that's musically important too! So the music we love, and even the music we could love in equal-tempered scales with more notes, relies on 3 interlocking facts about the numbers 5, 7 and 12.
All this started becoming clear to me when Scott Centoni wrote a little program in Sage to see how good the perfect fifth is in \(N\)-TET (the scale that divides the octave into N equally spaced notes).
When we use logarithms of frequency ratios, log(3/2) is a perfect fifth, while log(2)\(M/N\) is the \(M\)th note in \(N\)-TET. So, one way to formulate the question mathematically is: how well can we approximate log(3/2) by log(2)\(M/N\) for some integer \(M\)?
Alternatively: how well we can approximate log(3/2)/log(2) by a number of the form \(M/N\)?
Scott Centoni graphed the answer to the latter question and got the following:
You'll immediately notice a bunch of nice patterns in this chart. Most exciting to me are the descending bands consisting of either 6 even numbers or 6 odd numbers!
The bands of even numbers almost cross the x axis at multiples of 12, namely \(N\) = 12, 24, 36, 48, 60. The difference \(\Delta\) is the same for all these \(N\). Why? Well, 7/12 is so close to the magic number log(3/2)/log(2) that the best approximation to this magic number of the form \(M\)/24 is just 14/24 = 7/12. The best approximation of the form \(M\)/36 is just 21/36 = 7/12. And so on for quite a while... but not forever.
Also, if you look very carefully, you'll see \({|\Delta|}\) is smaller for \(N\) = 58 than \(N\) = 60. So while multiples of 12 provide the best even choices of N for a while, this doesn't last forever.
After a bit of glitchiness at the start, the bands of odd numbers come close to the x axis at numbers that are 5 more than a multiple of 12, namely 17, 29, 41, 53 and 65. Why? This is a bit more tricky. A good explanation of this was provided by gjm on Mathstodon, and I'll quote it below. Ultimately the reason is that 7 times 5 is almost a multiple of 12... yet that hint will probably seem quite cryptic until you read what gjm wrote.
But first, another visibly obvious pattern: the scales with \(N\) = 5, 10, 15, 20, 25, 30 and 35 notes all have the same Δ. Why? Well, 3/5 is fairly close to the magic number log(3/2)/log(2), so the best approximation to this number of the form \(M\)/10 is 6/10 = 3/5. And so on for a while. But it turns out 21/35 = 3/5 is not as close to the magic number as 20/35, so the pattern breaks down at this point.
You can also see that the scales with \(N\) = 7, 14, 21, 28 and 25 all have the same Δ. The reason is similar: 4/7 is close to the magic number.
Now for gjm's explanation of the bands of even and odd numbers, and further subtleties:
The pattern is a consequence of 7/12 being a good approximation for \(r = \log(3/2)/\log(2)\); there's a little bit less here than meets the eye.Write \(r = 7/12 + h\) where \(h\) is small (it's a little bit smaller than 1/600).
Suppose we're looking at a scale with \(N = 12n + k\) equally-spaced notes. Then the quality of the fifths depends on how close \((12n + k)r\) is to an integer. Well, \[ (12n+k)r = 7n + (7/12)k + (12n+k)h \] Call these terms \(A, B, C\).
\(A\) is always an integer so we can ignore it.
\(B\) mod 1 repeats with period 12. It's zero when \(k=0\), so multiple-of-12 scales are good as long as \(C\) stays small. It's -1/12 when \(k=5\), and \(C\) is positive, so \(N = 12k+5\) scales are also pretty good, though (at least initially) not as good, as long as \(C\) stays small.
When does the pattern break? Well, \(C\) gradually increases as \(N = 12n+k\) does. After it crosses \(1/24\), at \(N = 26\), \(B = -1/12\) becomes better than \(B = 0\); this doesn't break the pattern yet but it means that "29 is better than 36" even though "12 is better than 17". After \(C\) crosses 1/12, at \(N = 52\), \(B = -2/12\) becomes better than \(B = 0\), and this does break the pattern for even \(N\); \(N = 58\) beats \(N = 60\). After \(C\) crosses 3/24 at \(N = 76\), even \(N\) starts beating odd \(N\) again. After \(C\) crosses 2/12 at \(N = 103\), \(B = -3/12\) becomes better than \(B = -1/12\), which breaks the pattern for odd \(N\); \(N = 111\) is better than \(N = 113\).
The prose is a bit dense here, but it very much repays close reading. In particcular, why are equal-tempered scales with numbers of tones like
17 = 12 + 5
29 = 12 + 12 + 5
41 = 12 + 12 + 12 + 5
53 = 12 + 12 + 12 + 12 + 5
65 = 12 + 12 + 12 + 12 + 12 + 5
so good? It must be because these numbers times log(3/2)/log(2) are close to integers.
And why is that? Well, 7/12 is a tiny bit smaller than log(3/2)/log(2). So it must be because for n = 1,2,3,4,5 the number 12n + 5 times 7/12 is a tiny bit smaller than an integer. But that's equivalent to saying 5×7/12 is a tiny bit smaller than an integer. And that's equivalent to saying 5×7 is a bit less than a multiple of 12. And that's true: $$ 35 \approx 36 $$ While I'm talking about perfect fifths, I can't resist showing you Scott's similar chart for major thirds:
Now we are seeing how close some fraction of the form \(M\)/\(N\) comes to log(5/4)/log(2), since a major third has a frequency ratio of 5/4. While the patterns are striking, they are quite different than for perfect fifths! Presumably this is because there is no fraction with small denominator coming very close to log(5/4)/log(2).
Note that \(N\) = 53 gives a very good major third as well as a very good perfect fifth.
I also repeated Scott Centoni's analysis for minor thirds:
Now we are seeing how close some fraction of the form \(M\)/\(N\) comes to log(6/5)/log(2), since a minor third has a frequency ratio of 6/5.
If you're curious how Scott Centoni's plot for fifths would continue to equal-tempered scales with larger numbers of notes, here's how it looks for \(N\)-TET from \(N\) = 12 to \(N\) = 100:
and here's how it looks from \(N\) = 100 to \(N\) = 200:
In the first chart one of the 'descending bands of 6 odd numbers' actually has just 5 numbers. In the second chart, where the vertical scale is different, those bands are still there, but they're so steep that it's easier to see ascending bands of numbers.
There's a lot to explore here. But at least we've seen why the number
12 becomes important as soon you get interested in equal-tempered
scales with perfect fifths!
Just Intonation (Part 1)
$$
\begin{array}{lccc}
& \textbf{Pythagorean} && \textbf{just intonation} \\
\textbf{tonic} & 1 && 1 \\
\textbf{major 2nd} & 9/8 && 9/8 \\
\textbf{major 3rd} & 81/64 &>& 5/4 \\
\textbf{perfect 4th} & 4/3 && 4/3 \\
\textbf{perfect 5th} & 3/2 && 3/2 \\
\textbf{major 6th} & 27/16 &>& 5/3 \\
\textbf{major 7th} & 243/128 &>& 15/8 \\
\textbf{octave} & 2 && 2 \\
\end{array}
$$
In 'Pythagorean tuning’ all the frequency ratios between tones are products of powers of the primes 2 and 3. I explained this system in detail here. Because the largest prime it uses is 3, we say Pythagorean tuning is a form of '3-limit tuning'. One can imagine other forms of 3-limit tuning, though no other is as popular.
Now I want to start talking about '5-limit tuning’, where we allow frequency ratios to be products of powers of 2, 3 and 5.
The most popular form of 5-limit tuning is often called 'just intonation'. Broadly defined, just intonation refers to any form of tuning where the frequency ratios are rational numbers. But in practice people often use this term for the specific 5-limit tuning system shown in the above chart. This system was extremely popular in Renaissance music, but it continues to be important today, especially for string instruments.
It will take me more than one post to explore the mathematics of just intonation. There's a lot more to say here than for Pythagorean tuning. Having an extra prime to play with opens up many new subtleties!
The first thing to notice is that the 3rd, 6th and 7th notes in the major scale are simpler fractions in just intonation than in Pythagorean tuning — as you can see in the chart above.
This is probably why just intonation became popular. It was invented before 150 AD, when Ptolemy wrote about it in his book Harmonikon. But the even older Pythagorean tuning was great for medieval music, which emphasized fifths. Only when major thirds and sixths became popular in England starting in the 1400s with composers like John Dunstaple, and then spread into the rest of Europe, did just intonation take over!
To oversimplify: as the austere and sometimes rather harsh harmonies of medieval music softened to the sweeter sounds of Renaissance polyphony, the need for a better major thirds and sixths pushed just intonation to the fore. It seems to have dominated music until the 1500s! Then, as Baroque music called for more key changes, the beauty of simple fractions in a single major key was slowly sacrificed in favor of other virtues, leading ultimately to the utter dominance of equal temperament today.
In The Arithmetic of Listening, Kyle Gann writes:
History intervenes and alters musical practice. During the Hundred Years’ War (1337–1453), northern France was intermittently occupied by the English; the Maid of Orleans, Joan of Arc, turned the tide in France’s favor by helping get Charles VII crowned king in 1429, though she was burned at the stake in 1431. Before this highwater mark of the war, however, a great influx of English culture had already invaded France, establishing an English presence at such events as the Council of Constance, which lasted from 1414 to 1418 and reportedly attracted more than seventeen hundred musicians. Unlike the medieval French theorists, who were committed to Pythagoreanism, we have evidence that fifteenth-century English musicians used thirds as consonances in a five-limit tuning. Among other things, an influential English theorist, Walter Odington (fl. 1298–1316), had mentioned in his Summa de speculatione musice that major and minor thirds could be sung as consonances of 5/4 and 6/5, respectively, and that they were frequently so altered in actual practice. Also, the music of early fifteenth-century English composers such as John Dunstaple (c. 1390–1453) was noticeably more triadic than the contemporaneous French style; in the precise words of music historian Margaret Bent, in English music of the time, “3rds often seem to be ends in themselves while in contemporary continental music they are still straining for resolution.” This fuller, more consonant sound was termed “the contenance angloise” by a French contemporary who praised his countryman Guillaume Dufay and Gilles Binchois for adopting it. The English — historically less theoretically inclined than the French — were happily and intuitively filling their music with major thirds all over the place and tuning them nicely. Pythagorean tuning, so theoretically sound, began to seem practically deficient and, perhaps worse than that, old-fashioned.So let's think about those thirds a bit harder! As my chart above shows, the Pythagorean major third vibrates $$ \frac{81}{64} = 1.265625 $$ times as fast as the tonic (the first note in the scale). The just major third vibrates $$ \frac{5}{4} = 1.25 $$ times as fast as the tonic. So, the major third sounds a bit sharper in Pythagorean tuning! You can hear a Pythagorean major third here and a just major third here. If you're like me it may take a while to tell the difference.Under English influence, then, consonant, five-based thirds began to abound in fifteenth-century music throughout Europe. To deal with them required moving from a one-dimensional tuning concept to a two-dimensional one. Pythagorean tuning is one-dimensional: it can be diagrammed as a line of perfect fifths. In five-limit tuning we must weigh and jostle two desirable intervals: the 3/2 fifth and the 5/4 third.
To be precise, the Pythagorean major 3rd vibrates exactly $$ \frac{81/64}{5/4} = \frac{81}{80} = 1.0125 $$ times faster than the just major 3rd. And the major 6th and 7th also vibrate \(81/80\) times as fast in Pythagorean tuning as they do in just intonation! For the major 6th, the reason is that $$ \frac{27/16}{5/3} = \frac{81}{80} $$ while for the major 7th, we have $$ \frac{243/128}{15/8} = \frac{81}{80} $$ So this number, \(81/80\), is a big deal! It's called the 'syntonic comma', and I've already written about it here — it makes other interesting appearances in music.
But the big question is: where do the frequency ratios in just intonation come from? What principles do they follow, besides the fact that they're expressed in terms of powers of 2, 3 and 5?
These questions become even more interesting when we go from the 7-tone major scale to the 12-tone chromatic scale. Then the comparison between Pythagorean tuning and just intonation looks like this:
This is pretty complicated! But there are a lot of interesting patterns at work here. Whenever the Pythagorean and just intonation frequencies are not equal, the greater one divided by the smaller one equals the syntonic comma, \(81/80\). And can you spot the pattern in the 'greater than' and 'less than' signs?
I will have much more to say about just intonation and 5-limit tuning in posts to come. For now I recommend this:
It has more about the diatonic comma!
Just Intonation (Part 2)
Now let's dive into the beauties
of 5-limit
tuning — that is, tuning systems with frequency ratios that
are products of powers of only the primes 2, 3 and 5:
$$ 2^a\, 3^b \, 5^c , \qquad a,b,c \in \mathbb{Z} $$
We've already tackled 3-limit tuning, where we only got to use the
primes 2 and 3. Since multiplying the frequency by 2 merely raises a
tone by an octave, giving a tone that sounds 'just the same, only
higher', we were freed to focus on powers of 3/2. Multiplying the
frequency by 3/2 raises a tone by a fifth, so we got a diagram called
the circle
of fifths:
A point on this circle is a pitch class: two tones give the same pitch class if and only if their frequencies differ by a power of 2.
This circle shows that going up 6 fifths gets us to almost the same pitch class as going down 6 fifths. They're both very close to the tritone: the pitch class directly opposite our original frequency, 1. Taking advantage of these facts, we obtained the Pythagorean tuning system. For details, read my October 8th diary entry.
Let's try to mimic this procedure for 5-limit tuning! This gets a lot more interesting. Eventually it leads to a popular tuning system, or group of systems, called 'just intonation'.
Since multiplying the frequency by powers of 2 just changes the pitch by octaves, we can focus on powers of 3/2 and 5/4. As mentioned, the frequency ratio 3/2 is called a 'fifth', or more precisely a 'just perfect fifth'. Similarly, 5/4 is called a 'major third', or more precisely a 'just major third'. So, one way to think about 5-limit tuning is that it goes beyond 3-limit tuning by giving us access to the just major third.
It literally adds an extra dimension! Here we show a lattice with the number 1 at the center, where going one step east multiplies the number by 3/2 and going one step roughly northeast multiplies the number by 5/4:
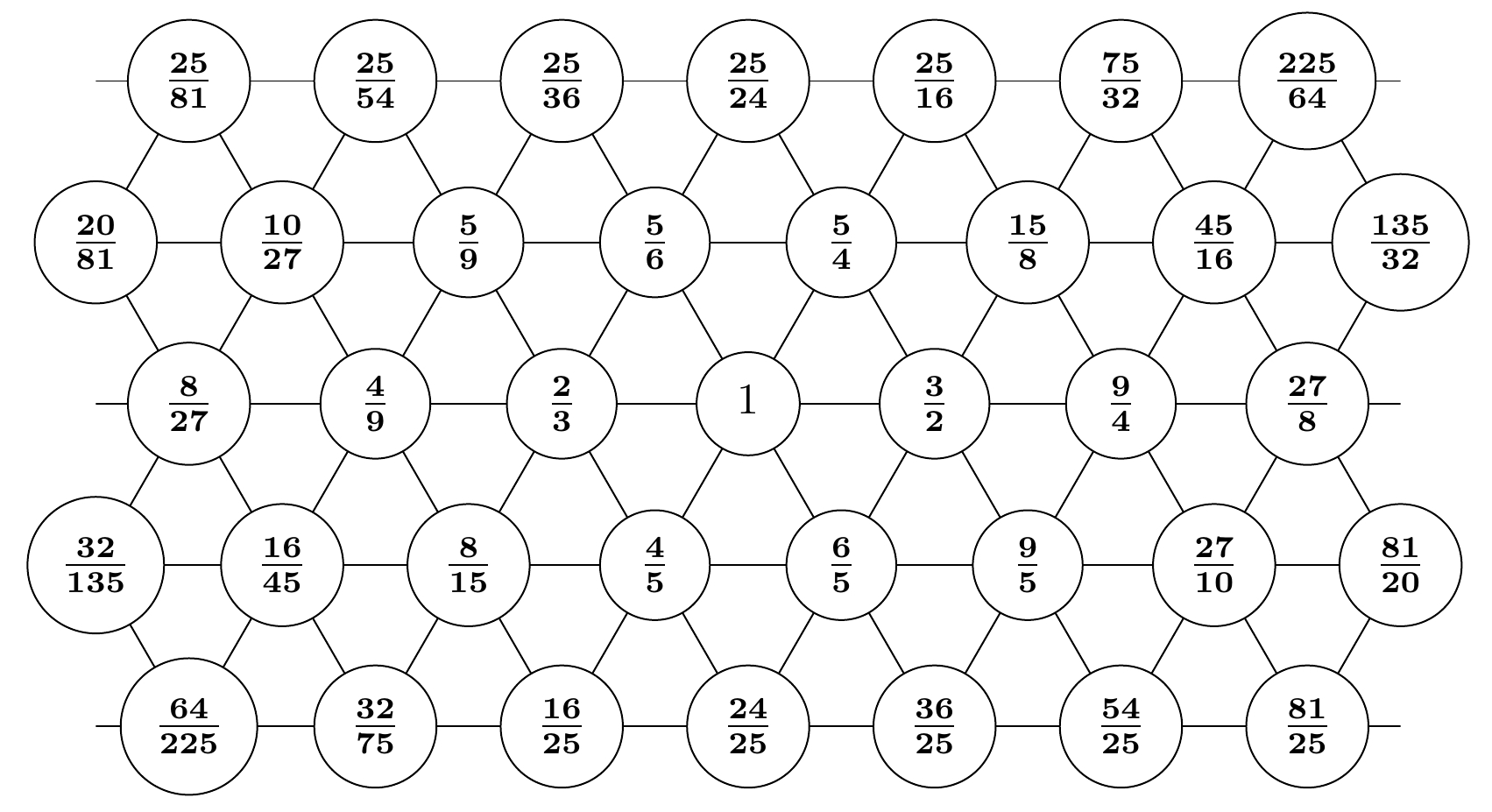
In musical terms, going one step east takes us up a fifth, while going one step roughly northeast takes us up a third.
Why did I draw a triangular lattice instead of a rectangular one? For now you can think of it as a random artistic decision, but the resulting diagram is called a Tonnetz, which means 'tone network' in German, and later we'll see how useful it is.
Now let's repeat what we did for Pythagorean tuning: let's see how far we have to go before we reach almost the same pitch class in more than one way.
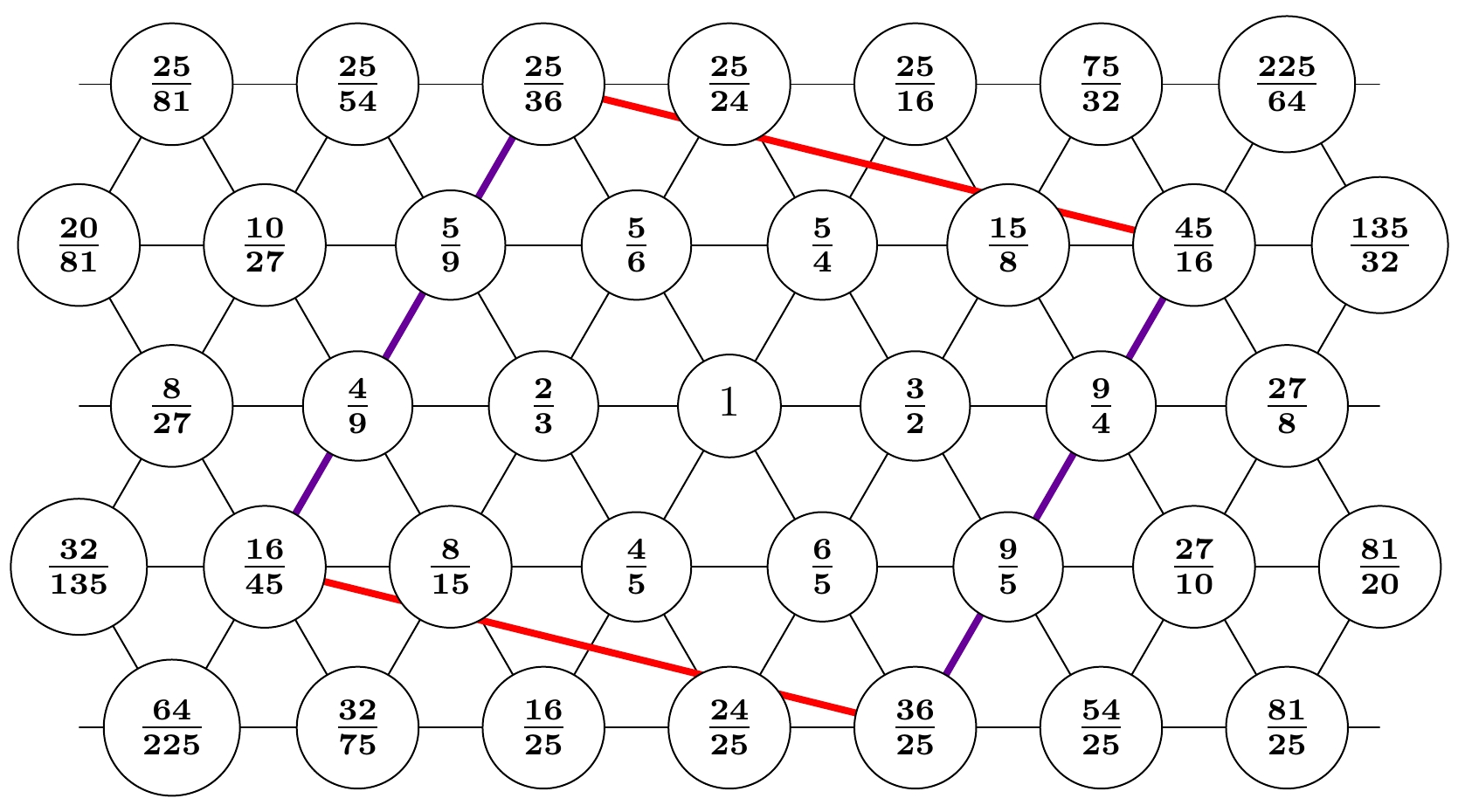
It turns out there are four ways to get very close to the tritone. These four ways are the corners of this parallelogram:
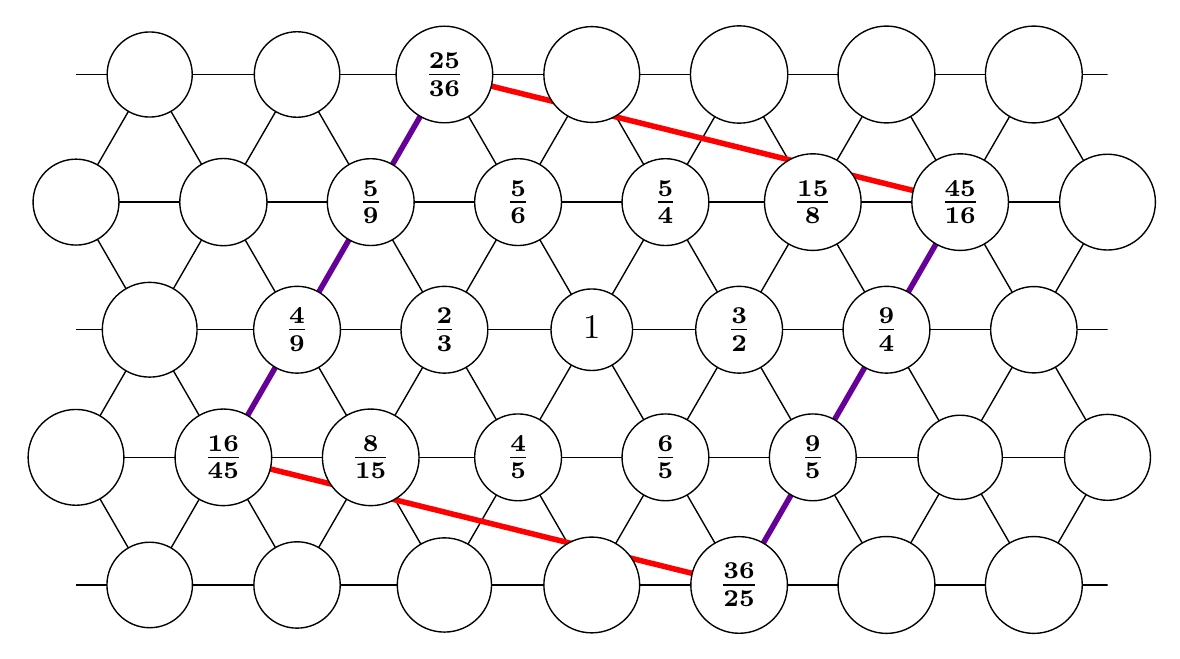
To clean up the picture, let's keep only the tones within this parallelogram (or on its boundary):
Now take these numbers and multiply them by suitable powers of 2 to keep them between 1 and 2. This gives tones lying between the tone at the center of the picture and the tone one octave above, as we'd want for a scale:
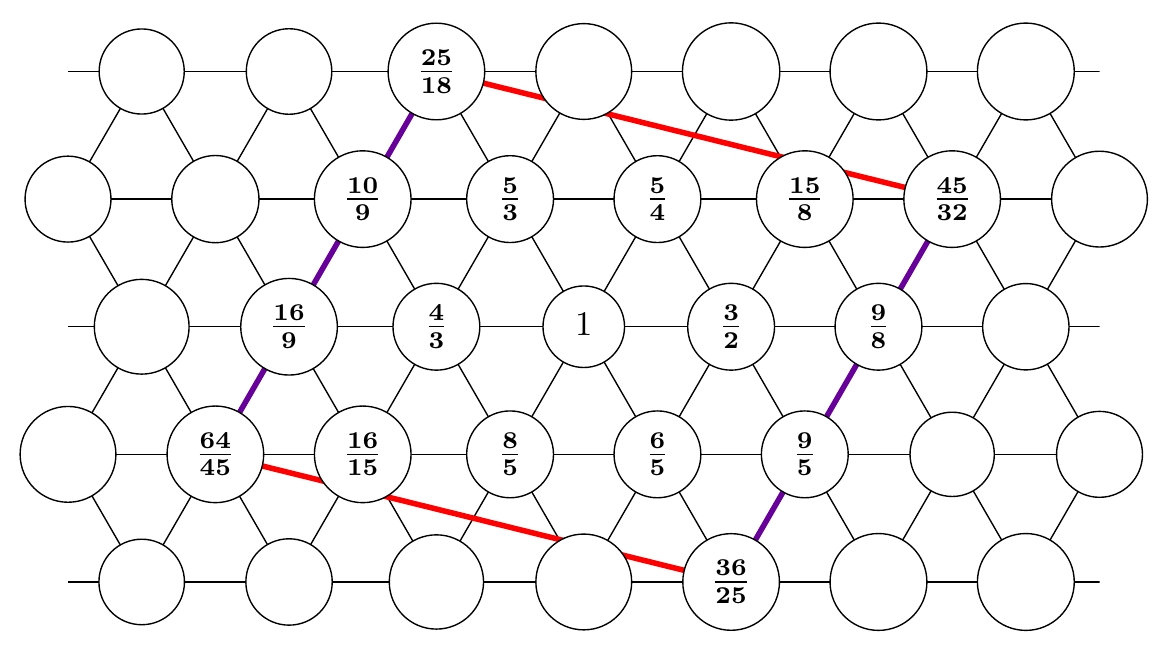
Now look at the numbers at the corners of this parallelogram! Let's check that they are close to a tritone, as I claimed. The tritone has frequency $$ \sqrt{2} \; \approx \; 1.414214 \dots $$ The corners are labeled by these numbers: $$ \begin{array}{ccl} \displaystyle{ \frac{25}{18} } &=& 1.38888\dots \\ \\ \displaystyle{ \frac{45}{32} } &=& 1.40625 \\ \\ \displaystyle{ \frac{64}{45} } &=& 1.42222 \dots \\ \\ \displaystyle{ \frac{36}{25} } &=& 1.44 \end{array} $$ So yes, they're pretty close!
Now for the cool part. Suppose we 'wrap around' this parallelogram to get a torus:
We identify the 4 tones on its left edge with the 4 tones on its right edge. Similarly, we identify the 2 tones on the top edge with the 2 tones on the bottom edge. And we're left with 12 tones — great for a 12-tone scale!
It's like magic, how the number 12 shows up yet again.
But there's a problem. The 4 tritones aren't equal, and the 4 numbers on the left edge don't equal the numbers on the right edge. They're close, but not quite equal! This is the same sort of problem that afflicted us in Pythagorean tuning, where we had two candidates for the tritone. But now we get 4 candidates for the tritone, 2 candidates for the major second, and 2 candidates for the minor seventh. So we get a scale with some choices: $$ \begin{array}{ll} \textrm{tonic} & \textrm{1} \\ \textrm{minor 2nd} & \textrm{16/15} \\ \textrm{major 2nd} & \textrm{10/9 or 9/8} \\ \textrm{minor 3rd} & \textrm{6/5} \\ \textrm{major 3rd} & \textrm{5/4} \\ \textrm{perfect 4th} & \textrm{4/3} \\ \textrm{tritone} & \textrm{25/18 or 45/32 or 65/45 or 36/25} \\ \textrm{perfect 5th} & \textrm{3/2} \\ \textrm{minor 6th} & \textrm{8/5} \\ \textrm{major 6th} & \textrm{5/3} \\ \textrm{minor 7th} & \textrm{16/9 or 9/5} \\ \textrm{major 7th} & \textrm{15/8} \\ \textrm{octave} & \textrm{2} \\ \end{array} $$ We need to make some decisions to get a specific scale.
But first, notice that the pattern would be clearer if we hadn't forced our frequencies to lie between 1 and 2 — that is, between the tonic and the octave. It's better if we force them to lie between \(1/\sqrt{2}\) and \(\sqrt{2}\) — that is, between the tritone below the tonic, and the tritone above. Then the Tonnetz has a beautiful symmetry:
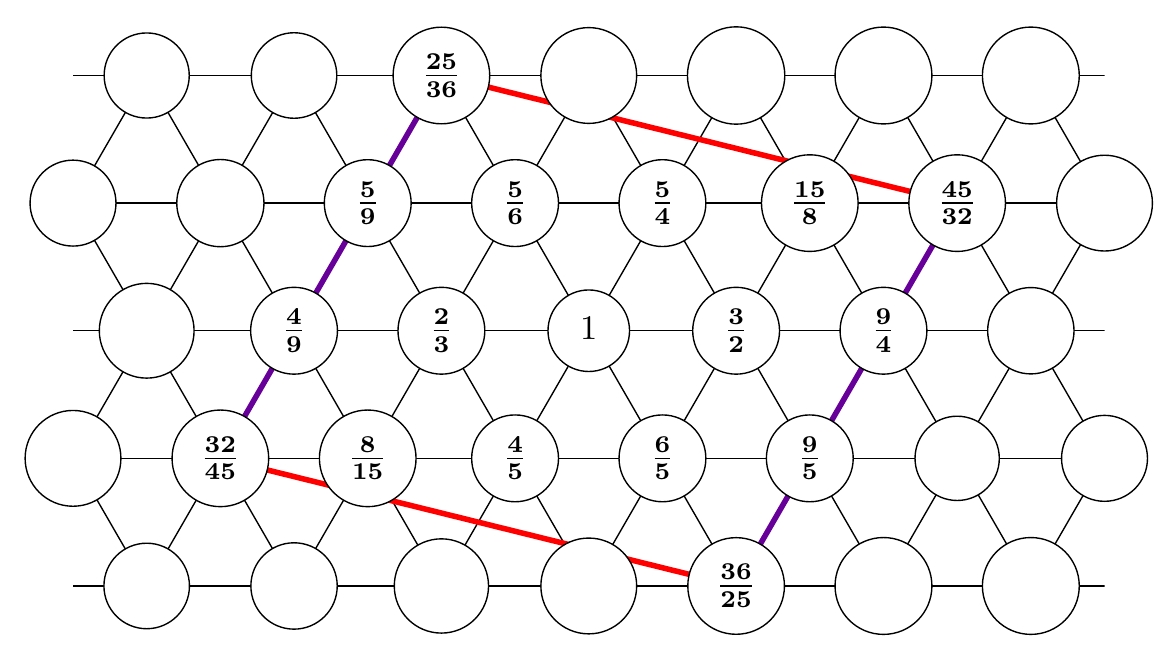
For any number in the parallelogram, its reciprocal appears in the opposite position! If we use these numbers instead, we get this nicer table: $$ \begin{array}{ll} \textrm{tritone} & \textrm{25/36 or 32/45} \\ \textrm{perfect 5th} & \textrm{3/4} \\ \textrm{minor 6th} & \textrm{4/5} \\ \textrm{major 6th} & \textrm{5/6} \\ \textrm{minor 7th} & \textrm{8/9 or 9/10} \\ \textrm{major 7th} & \textrm{15/16} \\ \textrm{tonic} & \textrm{1} \\ \textrm{minor 2nd} & \textrm{16/15} \\ \textrm{major 2nd} & \textrm{10/9 or 9/8} \\ \textrm{minor 3rd} & \textrm{6/5} \\ \textrm{major 3rd} & \textrm{5/4} \\ \textrm{perfect 4th} & \textrm{4/3} \\ \textrm{tritone} & \textrm{45/32 or 36/25} \\ \end{array} $$ Now we can start at the tonic and either climb up to the tritone, or climb down to the tritone... using the reciprocals of the same numbers!
Okay, enough perfect mathematical beauty. We have some difficult decisions to make: we have to choose which frequencies we'll actually use for our scale.
Let's recall how it worked for Pythagorean tuning. There we had two choices of tritone. One approach would be to choose both, calling one the augmented 4th and one the diminished 5th. But this gives us a total of 13 tones in our scale! To get a 12-tone scale people typically keep one choice of tritone and discard the other. This causes various difficulties, which I explained on October 8th.
All these issues become even more complicated in 5-limit tuning, since now we have 4 choices of tritone, 2 choices of major second, and 2 choices of minor seventh. I'll talk about this later.
For now, I just want to point out this. If we only want a major scale, our decisions become much easier: we just need to choose which major 2nd we want! There are just two choices: 10/9 and 9/8. 10/9 is called the small just whole tone and it sounds like this, while 9/8 is called the large just whole tone and it sounds like this.
9/8 is arguably the simpler fraction, and it's the one we used in Pythagorean tuning. If we use 9/8 as our major second we get the following scale, which I'll compare with Pythagorean tuning: $$ \begin{array}{lccc} & \textbf{Pythagorean} && \textbf{just intonation} \\ \textbf{tonic} & 1 && 1 \\ \textbf{major 2nd} & 9/8 && 9/8 \\ \textbf{major 3rd} & 81/64 &>& 5/4 \\ \textbf{perfect 4th} & 4/3 && 4/3 \\ \textbf{perfect 5th} & 3/2 && 3/2 \\ \textbf{major 6th} & 27/16 &>& 5/3 \\ \textbf{major 7th} & 243/128 &>& 15/8 \\ \textbf{octave} & 2 && 2 \\ \end{array} $$ This scale was discussed by Claudius Ptolemy in his famous book Harmonikon roughly around 150 AD, and it's called Ptolemy's intense diatonic scale.
I don't know why it's called 'intense', but this form of just intonation is intensely beautiful. It was very popular from around 1300 (at least in England) to at least 1550 (by which time it had spread to all of Europe). In 1558, in his influential text Le istitutioni harmoniche, the music theorist Gioseffo Zarlino proclaimed that this scale was "the only one that can reasonably be sung" — even though he was busy introducing a more complex tuning system for keyboards, called meantone temperament.
The rise of just intonation from 1300 to 1550 went hand in hand with increased use of major triads, which later became the bread and butter of classical music. A major triad on a tone consists of:
The amazing thing about Ptolemy's intense diatonic scale is that all the notes lie in major triads on the three most important notes in the scale: the tonic, the perfect fourth and the perfect fifth. You can see it in this chart here:
or if you prefer thinking in key of C major:
There are many more questions to answer when we go beyond Ptolemy's intense diatonic scale and construct a chromatic (i.e. 12-tone) scale based on 5-limit tuning. How do we choose between the 4 tritones? How do we choose between the two major 2nds — should we stick with the large just whole tone 9/8, or try the small just whole tone 10/9? How do we choose between the two minor 7ths? And what's the math underlying these choices?
I have a lot to say about this. There's also a lot more to say about
the Tonnetz. But all this will have to wait!
Just Intonation (Part 3)
Last time I said a bit about 'just
intonation': that is, tuning where the most important notes have
frequency ratios that are simple fractions. I focused on the
historically important case of '5-limit tuning', where the frequency
ratios are products of powers of primes ≤ 5.
I went a long way toward getting some popular scales in 5-limit tuning. I started by drawing a chart called a 'Tonnetz' where going east multiplies the frequency by 3/2, and going roughly northeast multiplies the frequency by 5/4:
Then, I kept only the numbers in a parallelogram whose corners are numbers very close to a tritone, that is, \(\sqrt{2}\) or \(1/\sqrt{2}\):
Then I multiplied these numbers by appropriate powers of 2 to make them lie between 1 and 2:
If we curl this parallelogram up into a torus, this torus has exactly 12 notes on it! To curl it up, we need to glue each note on the parallelogram's left edge to its partner on the right edge:
We also need to glue each note on the parallelogram's top edge to its partner on the bottom:
The problem is that not all the notes we're gluing together have the same frequency! Luckily, they're close.
How close are these notes, exactly? That's what I want to analyze today. Believe it or not, music theorists have thought about this for thousands of years and made up special terms to describe the answers.
First let's compare the notes on the left edge of the parallelogram to their partners on the right edge:
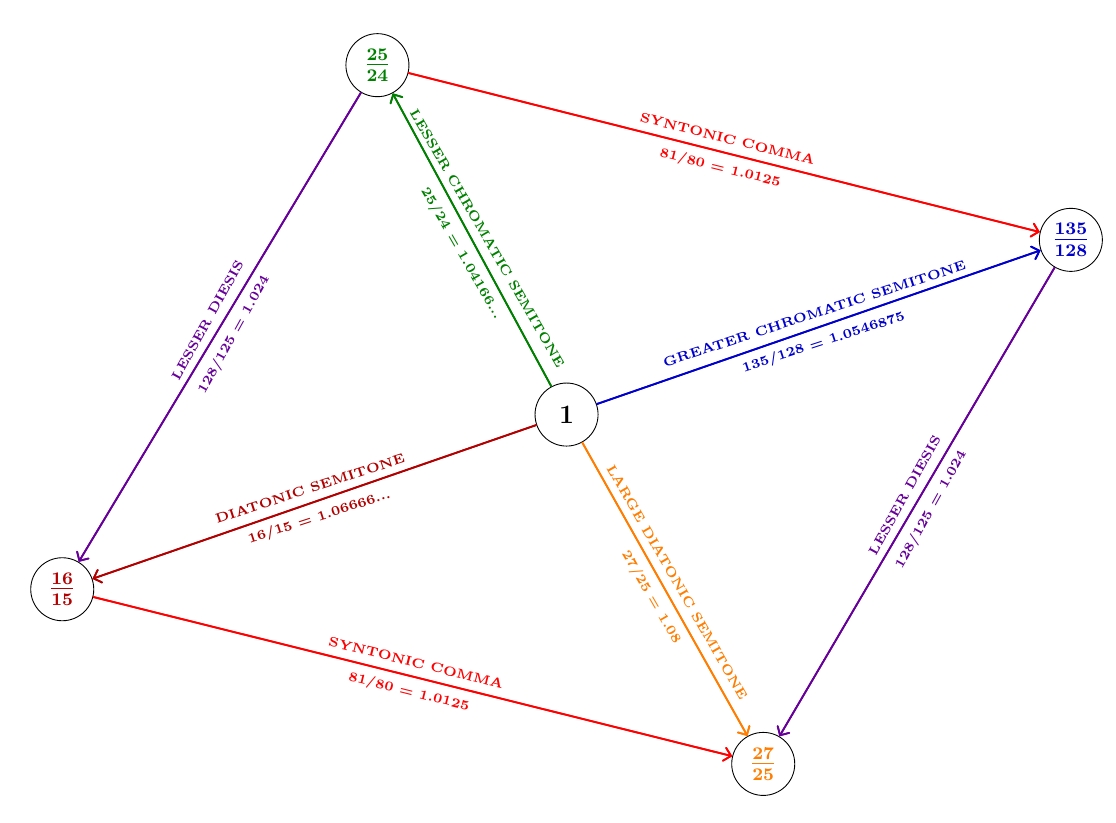
If we work out their frequency ratios, we see the notes on the right are a bit higher than those on the left: \[ \begin{array}{ccl} \displaystyle{\frac{45/32}{25/18}} &=& \displaystyle{\frac{81}{80}} \\ \\ \displaystyle{\frac{9/8}{10/9}} &=& \displaystyle{\frac{81}{80}} \\ \\ \displaystyle{\frac{9/5}{16/9}} &=& \displaystyle{\frac{81}{80}} \\ \\ \displaystyle{\frac{36/25}{64/45}} &=& \displaystyle{\frac{81}{80}} \end{array} \] We always get the same ratio! And it's our friend the syntonic comma: \[ 81/80 = 1.0125 \] This is no accident, of course: it's built into the structure of the Tonnetz. In music terminology, when we go up 4 just perfect fifths and then go down a just major third and 2 octaves, the frequency gets multiplied by \[ 3/2 \times 3/2 \times 3/2 \times 3/2 \times 4/5 \times 1/2 \times 1/2 = 81/80 \] which is the syntonic comma.
So: curling up the parallelogram means deciding whether to use tones on the its left edge and tones on its right edge — which forces us into the jaws of the syntonic comma.
Next let's compare the notes on the top edge of the parallelogram to their partners on the bottom edge:
If we work out their frequency ratios, we see the notes on the bottom are a bit higher than their partners on the top: \[ \begin{array}{ccl} \displaystyle{\frac{64/45}{25/18}} &=& \displaystyle{\frac{128}{125}} \\ \displaystyle{\frac{36/25}{45/32}} &=& \displaystyle{\frac{128}{125}} \end{array} \] Yet another glitch! This number is called the lesser diesis: \[ 128/125 = 1.024 \] 'Diesis' is a Greek word meaning 'leak' or 'escape' — though 'glitch' might be a more idiomatic translation. In music terminology, if you go up an octave and then go down 3 just major thirds, the frequency gets multiplied by \[ 2 \times 4/5 \times 4/5 \times 4/5 = 128/125 \] which is the lesser diesis. You can see how this works by staring at the Tonnetz.
In short, when we curl up the parallelogram we have some choices to make concerning the major second, the tritone and the major seventh: \[ \begin{array}{ll} \textrm{tonic} & \textrm{1} \\ \textrm{minor 2nd} & \textrm{16/15} \\ \textrm{major 2nd} & \textrm{10/9 or 9/8} \\ \textrm{minor 3rd} & \textrm{6/5} \\ \textrm{major 3rd} & \textrm{5/4} \\ \textrm{perfect 4th} & \textrm{4/3} \\ \textrm{tritone} & \textrm{25/18 or 45/32 or 65/45 or 36/25} \\ \textrm{perfect 5th} & \textrm{3/2} \\ \textrm{minor 6th} & \textrm{8/5} \\ \textrm{major 6th} & \textrm{5/3} \\ \textrm{minor 7th} & \textrm{16/9 or 9/5} \\ \textrm{major 7th} & \textrm{15/8} \\ \textrm{octave} & \textrm{2} \\ \end{array} \] For the major second we have two choices whose ratio is the syntonic comma: 10/9 and 9/8. In a symmetrical way, for the minor seventh below the tonic we have two choices whose ratio is the syntonic comma: 8/9 and 9/10. But we multiply these choices by 2 to get choices for the minor seventh above the tonic: 16/9 and 9/5.
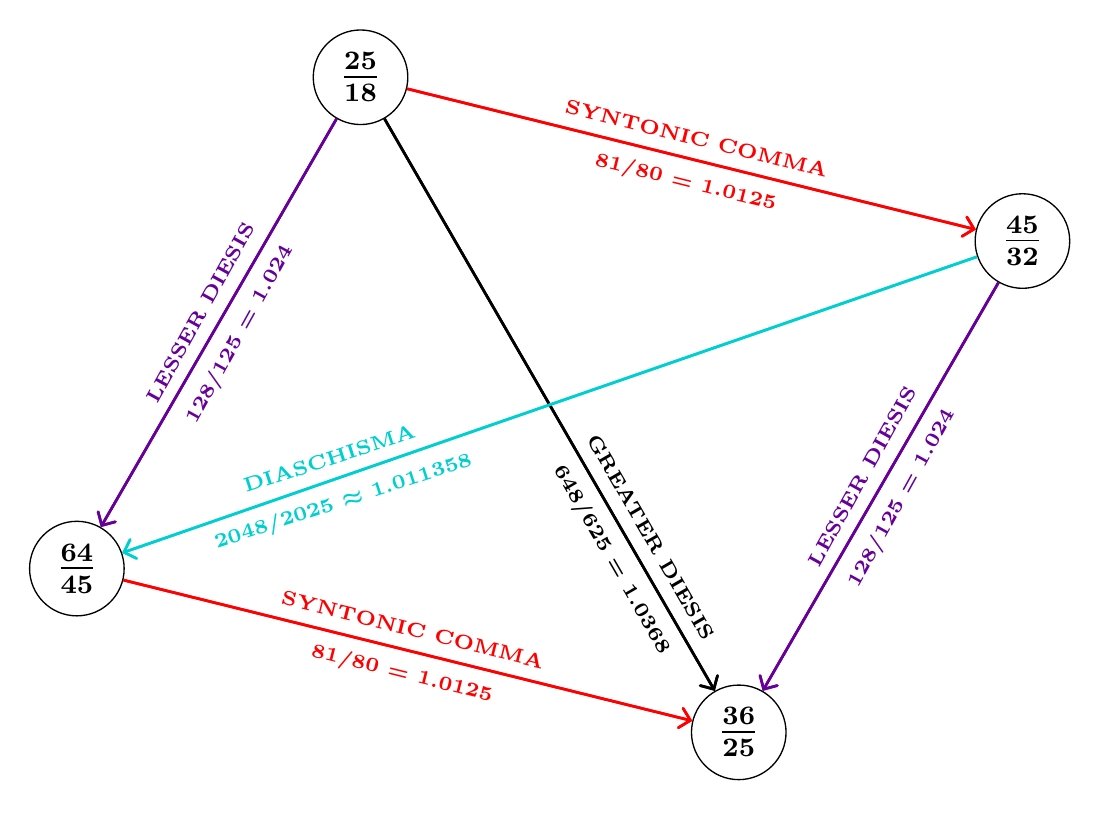
The biggest challenge involves the tritone, where we have four choices, coming from the corners of our parallelogram:
Here I've drawn arrows from lower tones to higher tones, and labeled each edge by the frequency ratio between the tones it connects.
The top and bottom edges have a frequency ratio of a syntonic comma, 81/80, while the left and right edges have a frequency ratio of a lesser diesis, 128/125. The diagonals also have standard names!
The diagonal from upper left to lower right gives a frequency ratio called the greater diesis: \[ \frac{36/25}{25/18} = \frac{648}{625} = 1.0368 \] In other words,
The diagonal from the upper right to the lower left gives a frequency ratio called the diaschisma: \[ \frac{64/45}{45/32} = \frac{2048}{2025} \approx 1.011358\dots \] In other words,
Apparently the diaschisma got its name from the physicist Helmholtz, but it was already studied by Boethius, who wrote a book called De musica in 510 AD. 'Schisma' means something like 'split', so I guess 'diaschisma' means 'the split between'.
Here you can see the syntonic comma, lesser and greater diesis, and diaschisma in decimals, to make it easier to compare how big they are:
Stay tuned for more!
Just Intonation (Part 4)
On November 6th we saw there are some
choices required when trying to pick a 12-note scale in just
intonation:
| tonic | 1 | |
| minor 2nd | 16/15 | |
| major 2nd | 10/9 or 9/8 | |
| minor 3rd | 6/5 | |
| major 3rd | 5/4 | |
| perfect 4th | 4/3 | |
| tritone | 25/18 or 45/32 or 64/45 or 36/25 | |
| perfect 5th | 3/2 | |
| minor 6th | 8/5 | |
| major 6th | 5/3 | |
| minor 7th | 16/9 or 9/5 | |
| major 7th | 15/8 | |
| octave | 2 |
Theoretically, there are
choices. But one is more popular than all the rest — at least in theory. Today I want to talk about that.
Beware: the heyday of just intonation was the Renaissance, but we have rather little information about the actual everyday practice of tuning back then. I wouldn't be surprised if many performers didn't give a fig about these numbers. What we mainly have is writings of theorists. They certainly knew their math. But I have not yet identified a passage in those old theoretical writings where someone commits to a specific 12-tone scale in just intonation. Quite possibly I haven't dug deep enough yet.
When I look around for such scales, modern authors tend to give this one:
| tonic | 1 | |
| minor 2nd | 16/15 | |
| major 2nd | 10/9 or 9/8 | |
| minor 3rd | 6/5 | |
| major 3rd | 5/4 | |
| perfect 4th | 4/3 | |
| tritone | 25/18 or 45/32 or 64/45 or 36/25 | |
| perfect 5th | 3/2 | |
| minor 6th | 8/5 | |
| major 6th | 5/3 | |
| minor 7th | 16/9 or 9/5 | |
| major 7th | 15/8 | |
| octave | 2 |
What's so good about this one?
First, 9/8 is a lot better than 10/9 for the major 2nd. I explained why already, at the end of my November 6th entry. Briefly, we need it so all the notes in the major scale lie in triads with frequency ratios 1 : 1.25 : 1.5. In C major these triads look like this:
Here the all-important 9/8 shows up as 9/4 since it's an octave up. And the chord in blue, containing the 9/4, has been incredibly important in western music ever since the Renaissance. You tend to play it right before the last chord in a piece of music! It's so bloody important that it has its own special name: the dominant chord.
Second, why should we pick 16/9 for the minor 7th instead of 9/5?
There could be valid musical reasons, but I don't know a compelling one, so I'll retreat to mathematics — a subject I actually know — and point out that this choice gives a scale that's symmetrical. That is, for each frequency in the scale, its reciprocal is also in the scale!
Now you may argue that this is baloney: the reciprocal of 16/9 is 9/16, and that's not on this list:
| tonic | 1 | |
| minor 2nd | 16/15 | |
| major 2nd | 9/8 | |
| minor 3rd | 6/5 | |
| major 3rd | 5/4 | |
| perfect 4th | 4/3 | |
| tritone | 45/32 | |
| perfect 5th | 3/2 | |
| minor 6th | 8/5 | |
| major 6th | 5/3 | |
| minor 7th | 16/9 | |
| major 7th | 15/8 | |
| octave | 2 |
True. You got me there! But 9/16 is just 9/8 divided by 2, which is on the list. Multiplying or dividing a frequency by a power of 2 gives another frequency in the same 'pitch class': they only differ by octaves. So musicians would say 9/16 really is in the scale, just an octave down.
In fact, the symmetry I'm talking about becomes a lot clearer if we list the tones in our scale going both up from the tonic and down from the tonic:
| perfect 5th | 3/4 | |
| minor 6th | 4/5 | |
| major 6th | 5/6 | |
| minor 7th | 8/9 | |
| major 7th | 15/16 | |
| tonic | 1 | |
| minor 2nd | 16/15 | |
| major 2nd | 9/8 | |
| minor 3rd | 6/5 | |
| major 3rd | 5/4 | |
| perfect 4th | 4/3 | |
Look: for each number on the list, its reciprocal on the list! Even better, the reciprocal of any 'major' tone is a 'minor' one, and vice versa. So flipping this scale upside down by taking reciprocals switches major and minor!
This is not a mere curiosity: it's a profound musical fact. Major is 'happy', minor is 'sad', and flipping one upside down gives the other... just like flipping a smile upside down gives a frown.
But you'll notice that to achieve this beautiful symmetry I left out the tritone. In fact, no single one of our original four choices of tritone:
gives a symmetrical scale. The reason is simple: none of these numbers is twice its reciprocal. To achieve that, we'd need to let the frequency of tritone be \(\sqrt{2}\). But that would be irrational.
So, people who want a symmetrical scale get it by choosing two tritones! They usually choose these two, which are reciprocals up to a factor of 2:
They call the smaller one the 'augmented 4th', and the larger one the 'diminished 5th'. Then we get a scale with this beautiful symmetry:
| diminished 5th | 32/45 | |
| perfect 5th | 3/4 | |
| minor 6th | 4/5 | |
| major 6th | 5/6 | |
| minor 7th | 8/9 | |
| major 7th | 15/16 | |
| tonic | 1 | |
| minor 2nd | 16/15 | |
| major 2nd | 9/8 | |
| minor 3rd | 6/5 | |
| major 3rd | 5/4 | |
| perfect 4th | 4/3 | |
| augmented 4th | 45/32 | |
Alas, we got this beautiful symmetry at the expense of having a 13-tone scale with two tones very close to each other. If we want 12 tones, we need to discard one. People usually discard the diminished 5th and keep the augmented 4th, namely 45/32.
Why? I'm not sure, but as a mathematician I'll note that the other choice gives a scale that's just an upside-down version of the scale people usually choose. So, I don't lose much by following the usual convention.
So there we are! We've made our choices as best we can. And since tuning theory is all about frustration, sticking to this approach gives us two choices, neither entirely pleasing:
and
Now let's examine each of these choices in more detail! I want to look at the spacings between the notes. Of course they are not equal: that only happens in equal temperament. But as you might expect, they have cool names. People have been studying this stuff for a long time.
Note that this scale has a beautiful up-down symmetry, as advertised!
There are four kinds of spacings between notes. Three are close to the usual spacing between notes on an equal-tempered piano. They're called half-tones, or semitones:
Our scale also has a tiny space between the augmented 4th and diminished 5th:
I discussed the diaschisma on November 9th, along with all the other tiny intervals between the four choices of tritone in just intonation:
Now you can see why Boethius grappled with the diaschisma as early as 510 AD, though it was named much later by the great mathematician and physicist Helmholtz.
Here's another picture of our scale, which also shows the tones not chosen, in gray:
The up-down symmetry is very visible here.
But what if we create a 12-tone scale by removing the diminished 5th, as people seem to usually do? Then we break the up-down symmetry, and get this scale:
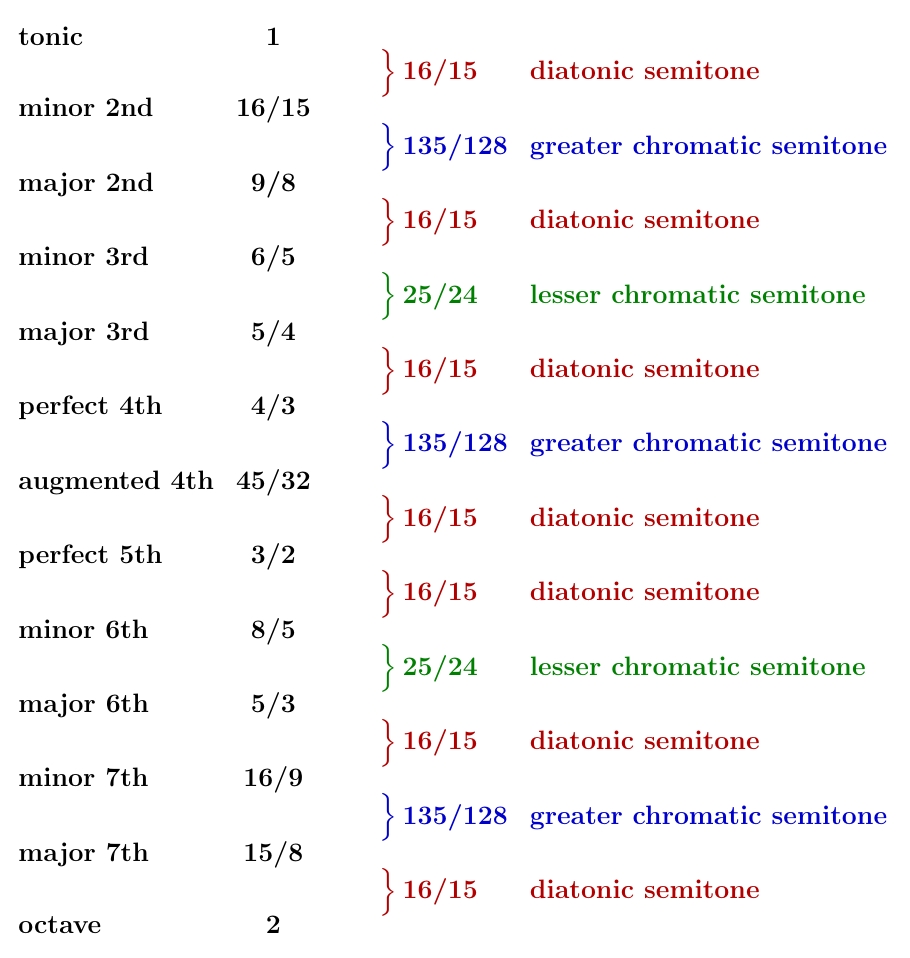
This seems to be the most popular 12-tone just intonation scale. For example, it was favored by Newton and Mersenne.
Compared to the symmetrical 13-tone scale it's based on, this scale has an extra diatonic semitone. There's a reason for that: when we discard the diminished 5th and jump all the way from the augmented 4th to the 5th, we stick the diaschisma onto one of the greater chromatic semitones we had. This gives a diatonic semitone, since
or in terms of numbers: $$ \displaystyle{ \frac{16}{15} = \frac{135}{128} \times \frac{2048}{2025} } $$
Okay, we have reached a natural stopping point for today. I have described the most popular 12-tone scale that uses just intonation! We have seen the frequencies of all its notes. We have also studied the spaces between its notes. What more could we want?
Well, remember that we chose two of the four possible tritones to be the augmented 4th and diminished 5th, namely these:
What if we chose the other two? We'd get another symmetrical 13-tone scale, and discarding its augmented 5th we'd get another 12-tone scale. What's wrong with that scale?
It actually is worse in some objective sense. But to see how, we need to look at it!
So, let's create a symmetrical 13-tone scale where we use the other two tritones as our augmented 4th and diminished 5th:
It looks like this:
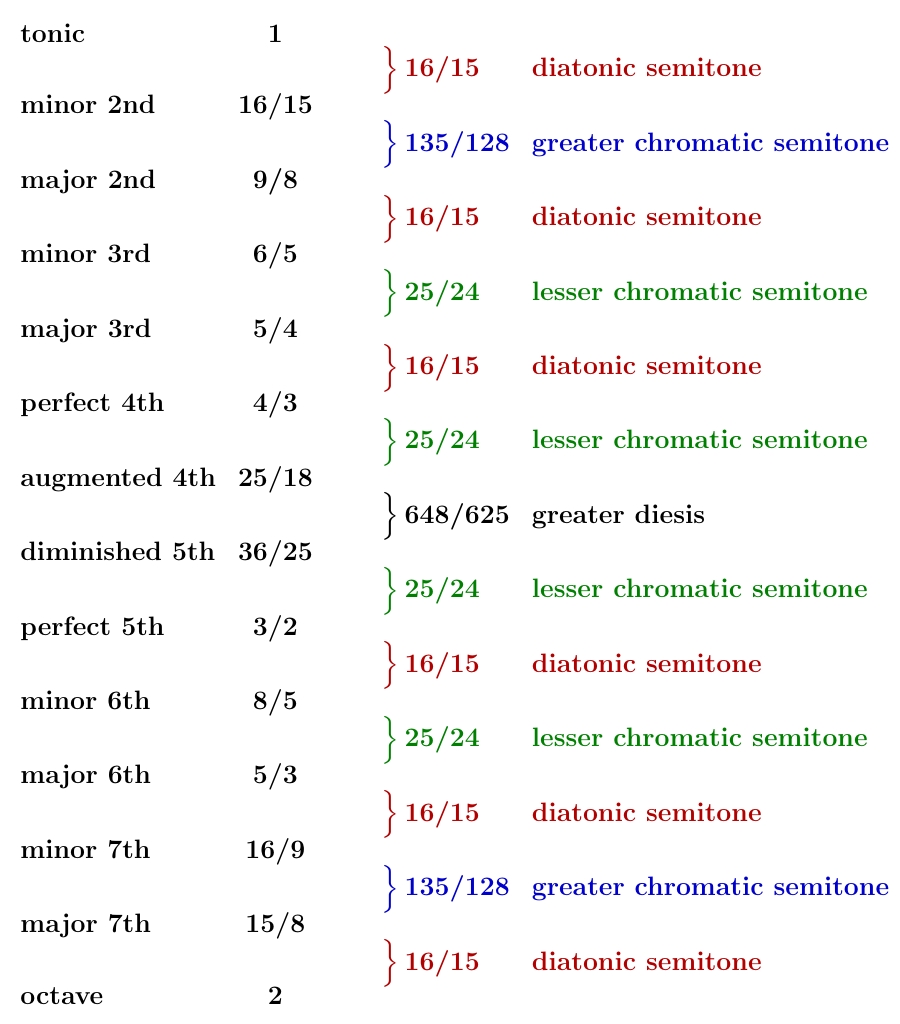
Now the space between the augmented 4th and diminished 5th is bit bigger! It's changed from the diaschisma to a larger interval:
The two neighboring spaces have therefore shrunk. In fact they've shrunk from greater chromatic semitones to lesser chromatic semitones, since
or in terms of numbers:
$$ \displaystyle{ \left(\frac{135/128}{25/24}\right)^2 = \frac{648/625}{2048/2025} } $$
Wild!
This scale doesn't look worse than our other symmetrical 13-tone scale: at least, not to me. It's when we create a 12-tone scale by discarding the diminished 5th that something funny happens.
Let's do it: let's throw out the diminished 5th! Then we get this scale:
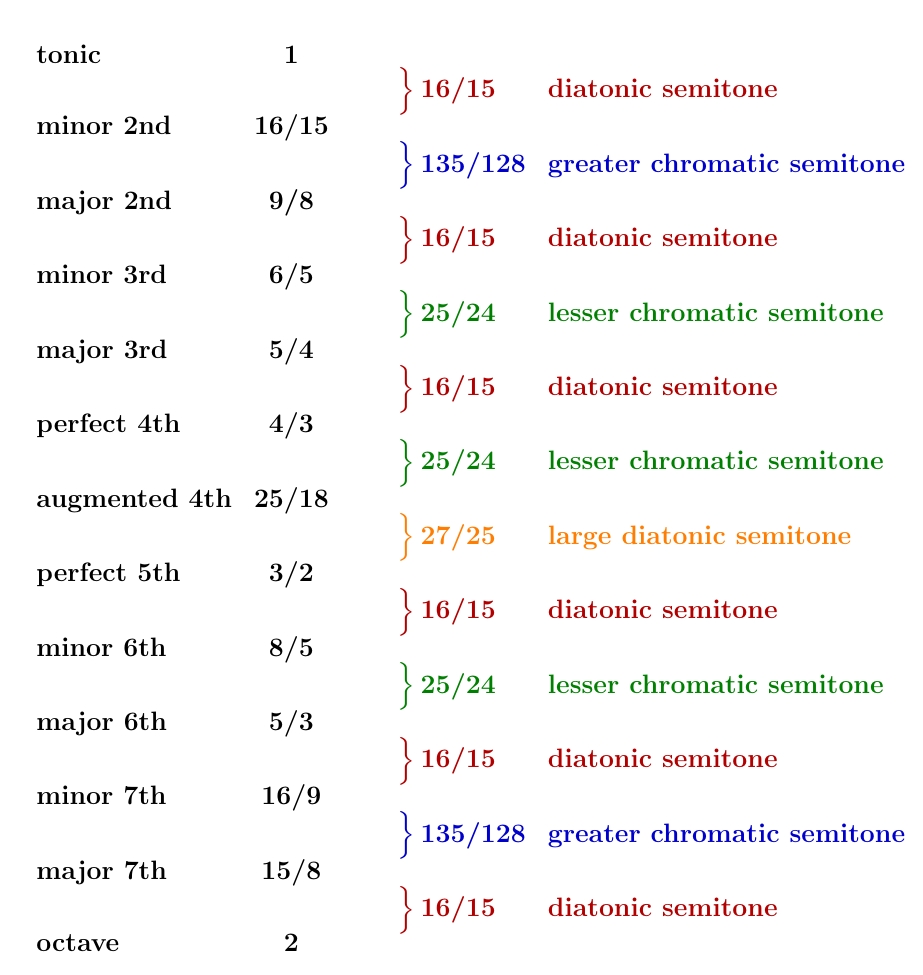
Look! Not only does it lack up-down symmetry, as we expect — there's something else odd about it. It has four kinds of semitone! Yes: it has the three we've already seen, but also this:
This is significantly bigger than the other three semitones. And it's nasty to have to keep track of yet another kind of semitone. So, arguably, this scale is not as nice as the one people actually settled on. But the large diatonic semitone is still significant in music theory. Since we got it by sticking the greater diesis onto a lesser chromatic semitone, we get:
or in terms of numbers:
$$ \displaystyle{ \frac{27}{25} = \frac{25}{24} \times \frac{648}{625} } $$
By the way: if you find it impossible to remember these crazy numbers and the web of mathematical relations connecting them, don't feel bad. So do I! Next time I'll summarize all these mathematical relations using some pretty pictures.
Puzzle 1. As we've seen, the most popular 12-tone just intonation scale has 7 diatonic semitones, 3 greater chromatic semitones, and 2 lesser chromatic semitones:
By permuting these semitones we can get many other scales. How many different scales can we get this way?
Puzzle 2. Our second, less popular almost symmetrical 12-tone just intonation scale has 6 diatonic semitones, 2 greater chromatic semitones, 3 lesser chromatic semitones and 1 large diatonic semitone:
How many other scales can we get by permuting these semitones?
Of course these questions are warmups for a bigger question:
Puzzle 3. How many 12-tone scales are there where the spacing between each pair of successive notes is either a diatonic semitone, a greater chromatic semitone, a lesser chromatic semitone or a large diatonic semitone?
These alternative scales may seem pointless, but in fact some have been studied by famous music theorists or mathematicians. For example, in 1694 William Holder discussed a scale with 5 lesser chromatic semitones, no greater chromatic semitones, 4 diatonic semitones and 3 large diatonic semitones!
(For answers to these puzzles see my December 29, 2025 diary entry.)
Just Intonation (Part 5)
On November 9th we saw that in just
intonation there are four candidates for
the tritone. They
are simple fractions close to the square root of 2. We saw that they
lie at the corners of a parallelogram in a diagram called the tone
network, or Tonnetz:
To get a 12-tone scale from this parallelogram, we need to think about the tiny differences between these 4 numbers. More precisely, since our ear hears frequency ratios, we need to think about the ratios of these 4 numbers, which are close to 1. Because people have been thinking about them for centuries, they all have cool names:
Here I've drawn arrows from tones of lower frequency to tones of higher frequency, and labeled these arrows by the frequency ratios.
In Part 4 we studied how to get a 12-tone scale in just intonation. I described two ways. In the most popular way, the spaces between tones come in 3 different sizes. But I also described another way, which is a bit less nice because the spaces between notes come in 4 different sizes. These 4 sizes are called semitones, but each has it own individual name.
Now for something cool. Let's draw a parallelogram with these 4 semitones as corners. Let's draw arrows from those of lower frequency to those of higher frequency, and label these arrows by the frequency ratios:
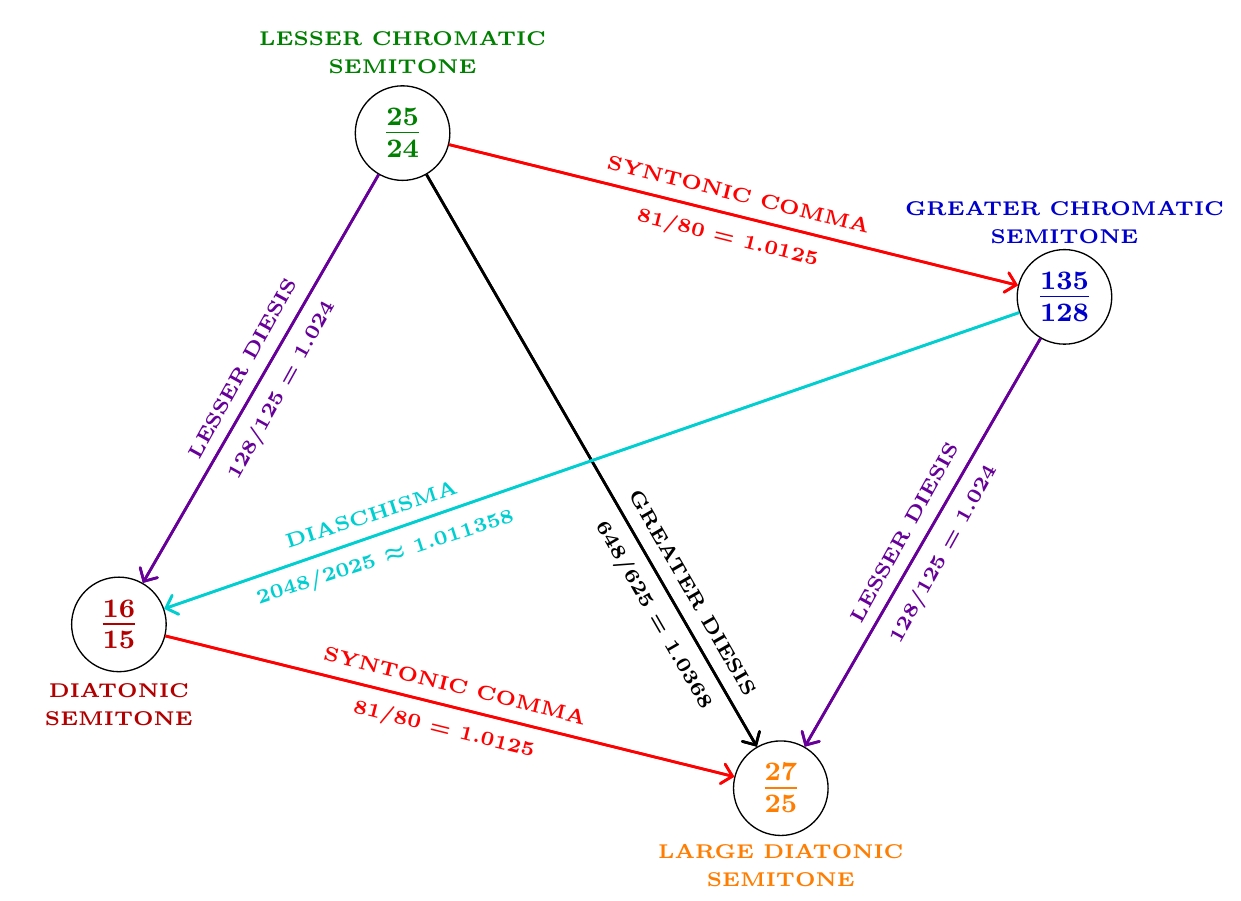
Hey! The frequency ratios are just the same as in our other parallelogram!
What's going on?
Here's what: when we take the parallelogram of semitones and shift it up a perfect fourth, we get the parallelogram of tritones!
Let me spell that out more carefully. It turns out that each tritone in our first parallelogram is a semitone higher than the perfect fourth, 4/3. But there are 4 kinds of semitone, so we get 4 kinds of tritone: $$ \begin{array}{ccl} \displaystyle{ \frac{25}{24} \times \frac{4}{3}} &=& \displaystyle{\frac{25}{18}} \\ \\ \displaystyle{ \frac{135}{128} \times \frac{4}{3}} &=& \displaystyle{\frac{45}{32}} \\ \\ \displaystyle{ \frac{16}{15} \times \frac{4}{3}} &=& \displaystyle{\frac{64}{45}} \\ \\ \displaystyle{ \frac{27}{25} \times \frac{4}{3}} &=& \displaystyle{\frac{36}{25}} \end{array} $$ So there's less going on than meets the eye: everything fits together.
We can also draw our parallelogram of semitones with the tonic, that is the frequency 1, in the middle:
The arrows here should make you think of vector addition, where adding two sides of a triangle can give you the third if the arrows are pointing the right way. But here the edges are just numbers, and we combine them by multiplying them. So each triangle in this picture gives an identity:
So you don't need to remember all these identities: they're all in the picture!
Our earlier picture describes the frequency ratios of the semitones at the opposite corners of this parallelogram:
So it gives two more identities:
But again, the picture relieves you of the need to remember the identities. And you don't need to learn all the fancy names for things if you don't want to!
It's a bit like trigonometry. You can learn the names of lots of trig functions and identities relating them. Or you can just learn to understand the sine and cosine and the identities relating those. Or you can just learn to understand the function \(\exp(ix)\) and a couple of identities it obeys. The more you use trigonometry, or the more you enjoy it, the more it pays to remember. If you really love trigonometry and its history, learn about the versine:
Or go hog wild: learn about the haversine, the coversine, the vercosine, the covercosine, and more!
But if you don't want to learn this stuff, it's fine to take a more economical approach.
Puzzle 1. I drew the number 1 at the center of this parallelogram of semitones:
But what should really be at the center?
Puzzle 2. If we use the same logic, what should be at the center of this parallelogram of tritones?
Newton did his work on this in college when he was 22. This was 1665, the year he later fled Trinity College to avoid the Great Plague, went to the countryside, invented calculus, began thinking about gravity, and discovered that a prism can recombine colors of light to make white light.
Given this, I can't resist classifying all possible scales of this sort. Today we'll see that by a certain precise definition, there are 174,240 such scales! It will take a bit of combinatorics to work this out. Among this large collection of scales we will also find smaller sets of scales with nice properties. But I still don't know why those mathematicians chose the scales they did.
In studying this, and indeed in all my work on just intonation, I was greatly helped by this wonderful paper:
It's full of interesting diagrams:
Anyway, let's get going!
On November 15th, I examined the choices involved in building a just intonation scale. I described a general recipe for building such scales. These leads to 2 × 4 × 2 = 16 different scales, based on how you make the choices here:
| tonic | 1 | |
| minor 2nd | 16/15 | |
| major 2nd | 10/9 or 9/8 | |
| minor 3rd | 6/5 | |
| major 3rd | 5/4 | |
| perfect 4th | 4/3 | |
| tritone | 25/18 or 45/32 or 64/45 or 36/25 | |
| perfect 5th | 3/2 | |
| minor 6th | 8/5 | |
| major 6th | 5/3 | |
| minor 7th | 16/9 or 9/5 | |
| major 7th | 15/8 | |
| octave | 2 |
Newton's scale is one of these 16. Marin Mersenne had created the same scale in 1636, but Newton probably didn't know this. In fact I studied this scale in Part 4, where I claimed that it's the most popular just intonation scale of all! It's hard to be sure of that — but I certainly think it's the nicest one.
Here it is:
The intervals between the notes come in 3 different sizes, which we will discuss soon. On November 15, 2024, I explained some reasons this scale is nice. For example, the intervals here are nearly palindromic! The first interval is the same as the last, and so on — except right at the middle of the scale, the 'tritone', where this symmetry is impossible because it would force \(\sqrt{2}\) to be a rational number.
In Part 4, I also considered another less popular scale among the 16 generated by my recipe:
In this one the intervals come in 4 different sizes! Let's make up abbreviations for them. In order of increasing size, they are:
With this notation, Newton's scale is
I'll say this scale has type (2,3,7,0) since it has 2 c's, 3 C's, 7 d's and 0 D's. The less popular scale I mentioned is
This scale has type (3,2,6,1). Arguably this scale is worse, because the large diatonic semitone is quite large compared to all the rest.
Muzzulini also describes some other just intonation scales. Here's one that Nicolas Mercator created around 1660 — not the Mercator with the map, the one who discovered the power series for the logarithm:
Here's one that the music theorist William Holder wrote down in 1694:
This has three diatonic semitones — the most possible! It's of type (5,0,4,3).
Leonhard Euler came up with this scale in 1739:
This has type (3,2,6,1).
It would be interesting to find out, if possible, why various authors chose the scales they did. Did they scan the universe of possibilities and try to pick a scale that was optimal in some way — or did they did they just make one up? Answering this would require some historical investigation.
Muzzulini also describes some other just intonation scales. Here's one that Nicolas Mercator created around 1660---not the Mercator with the map, the one who discovered the power series for the logarithm:
Puzzle 1. As we've seen, the most popular 12-tone just intonation scale is of type (2,3,7,0). That is, it has 2 lesser chromatic semitones, 3 greater chromatic semitones, 7 diatonic semitones, and no large diatonic semitones. By permuting these semitones we can get many other scales. How many different scales can we get this way?
Answer. We have a 12-element set and we're asking: in how many ways can we partition it into a 2-element set, a 3-element set and a 7-element set? This is the kind of question that multinomial coefficients were designed to answer. The answer is
\[ \qquad \qquad \displaystyle{ \frac{12!}{2! \cdot 3! \cdot 7!} = 7920. } \qquad \qquad █ \]
Puzzle 2. Our second, less popular 12-tone just intonation scale is of type (3,2,6,1): it has 3 lesser chromatic semitones, 2 greater chromatic semitones, 6 diatonic semitones and 1 large diatonic semitone. How many other scales can we get by permuting these semitones?
Answer. By the same reasoning, we have
\[ \displaystyle{ \frac{12!}{3! \cdot 2! \cdot 6! \cdot 1!} = 55,440 } \]
such scales. █
These puzzles were warmups for a bigger question:
Puzzle 3. How many 12-tone scales are there where the spacing between each pair of successive notes is either a lesser chromatic semitone, a greater chromatic semitone, a diatonic semitone, or a large diatonic semitone?
Answer. The only types of scales allowed are quadruples \((i,j,k,\ell)\) of nonnegative integers where \[ \displaystyle{ \left(\frac{25}{24}\right)^i \left( \frac{135}{128} \right)^j \left( \frac{16}{15} \right)^k \left( \frac{27}{25} \right)^\ell = 2 }\]
or equivalently, \[ \displaystyle{ i \ln\left(\frac{25}{24}\right) + j \ln\left( \frac{135}{128} \right) + k \ln\left( \frac{16}{15} \right) + \ell \ln \left( \frac{27}{25} \right) = \ln 2. } \]
The four numbers \[ \ln\left(\frac{25}{24}\right), \ln\left( \frac{135}{128} \right),\ln\left( \frac{16}{15} \right), \ln \left( \frac{27}{25} \right) \]
span the 3-dimensional rational vector space with basis \(\ln 2, \ln 3, \ln 5,\) so they must obey one linear relation with integer coefficients (and others following from this one). This relation is \[ \displaystyle{ \ln\left(\frac{25}{24}\right) + \ln \left( \frac{27}{25} \right) = \ln\left( \frac{135}{128} \right) + \ln\left( \frac{16}{15} \right).} \]
This says cD = Cd: the lesser chromatic semitone followed by the large diatonic semitone takes you up to a frequency 9/8 higher, just like the greater chromatic semitone followed by the diatonic semitone.
This means that if a type \((i,j,k,\ell)\) is allowed, so is \((i+1,j-1,k-1,\ell+1)\) if \(j-1,k-1 \ge 0\). Furthermore, it means this move (and its inverse) can take you from any allowed type to all other allowed types.
So, let's start with the type where \(\ell,\) the number of large diatonic semitones, is as small as possible. This is our friend \[ (2,3,7,0). \]
We can get all other allowed types by repeatedly adding 1 to the first and last component of this vector and subtracting 1 from the other components. Thus, these are all the allowed types:
We can now use the methods of Puzzles 1 and 2 to count the scales of each type. We get:
\(\displaystyle{ \frac{12!}{2! \cdot 3! \cdot 7! \cdot 0!} } \) = 7,920 scales of type (2,3,7,0),
\(\displaystyle{ \frac{12!}{3! \cdot 2! \cdot 6! \cdot 1!} } \) = 55,440 scales of type (3,2,6,1),
\(\displaystyle{ \frac{12!}{4! \cdot 1! \cdot 5! \cdot 2!} } \) = 83,160 scales of type (4,1,5,2),
\(\displaystyle{ \frac{12!}{5! \cdot 0! \cdot 4! \cdot 3!} } \) = 27,720 scales of type (5,0,4,3).
So, we get a total of
This is a ridiculously large number of scales! But of course, not all are equally good. Let's impose some extra constraints.
The whole point of just intonation was to make the third equal to 5/4, and we also want to keep the fourth at 4/3 and the fifth at 3/2, as we had in Pythagorean tuning. When it comes to the second, either 10/9 or 9/8 are considered acceptable in just intonation. I like 9/8 a bit better, so let's do this:
Puzzle 4. How many 12-tone scales are there where the spacing between each pair of successive notes is either a lesser chromatic semitone, a greater chromatic semitone, a diatonic semitone, a large diatonic semitone, and:
Answer. With these constraints there are 1,600 allowed scales. The idea is this:
So, we get 4 × 2 × 1 × 4 × 500 = 1,600 scales of this sort. █
All these scales have the second being the greater major second, 9/8. But you might prefer the lesser major second, 10/9. So let's think about that:
Puzzle 5. What about the same question as before, but where we constrain the second to be 10/9 instead of 9/8?
Answer. Again there are 1600 scales. In Puzzle 4 our scales went up from 1 to 9/8 by choosing two semitones that multiply to 9/8, and then from 9/8 to 5/4 by choosing two that multiply to 10/9. Now the only difference is that we're going things in the other order: we're going up from 1 to 10/9 by choosing two semitones that multiply to 10/9, and then from 10/9 to 5/4 by choosing two that multiply to 9/8. So the overall count is the same as before. █
Since they differ only by switching some semitones, the 1,600 scales with a greater major second have the same distribution of types as the 1,600 with a lesser major second. Using a computer, I calculated that in each case there are
How can we pick out a smaller number of 'better' scales? We've imposed a lot of constraints on the tones from the first to the fifth, but none on the tones above that. To impose constraints on the higher tones, we can demand that our scale be palindromic, except that we can't require that the interval from the fourth to the tritone equals the interval from the tritone to the fifth, because \(\sqrt{2}\) is irrational. So, I'll call scales with the following properties nearly palindromic:
Puzzle 6. How many nearly palindromic 12-tone scales are there where the spacing between each pair of successive notes is either a lesser chromatic semitone, a greater chromatic semitone, a diatonic semitone, a large diatonic semitone, and:
Answer. There are 32 scales with these properties. First note that the above properties force other facts:
Thus, we have the following choices:
and from then on, our choices are forced by the nearly palindromic nature of the scale. There are thus a total of
4 × 2 × 1 × 4 = 32
choices. █
These 32 scales come in two kinds:
The most popular just intonation scale is of the first kind. Newton's scale is of the second kind.
All 32 of these scales use the greater major second. A similar story holds with the lesser major second.
Puzzle 7. How many nearly palindromic 12-tone scales are there where the spacing between each pair of successive notes is either a lesser chromatic semitone, a greater chromatic semitone, a diatonic semitone, a large diatonic semitone, and:
Answer. By the symmetry we used to answer Puzzle 5, this question has the same answer as Puzzle 6: there are again 32 choices. █
These 32 scales again come in two kinds:
If you've made it this far, congratulations! I was lured in by how many famous mathematicians had studied this subject, and I wanted to join the fun.
Quarter-Comma Meantone (Part 1)
I've spent the last few weeks drawing pictures of tuning systems, since I realized this is a good way to show off their mathematical beauty. Now I'll start deploying them!
I've already written about the first two hugely important tuning systems in Western music: Pythagorean tuning and just intonation. It's time to introduce the third: 'quarter-comma meantone’.
But first, remember the story so far!
Pythagorean tuning may go back to Mesopotamia, but it was widely discussed by Greek mathematicians — perhaps including Pythagoras, whose life is mainly the stuff of legends written down centuries later, but more certainly Eratosthenes, and definitely Ptolemy. It was widely used in western Europe in the middle ages, especially before 1300.
The principle behind Pythagorean tuning is to start with some pitch and go up and down from there by 'just fifths' — repeatedly multiplying and dividing the frequency by 3/2 — until you get two pitches that are almost 7 octaves apart. Here I'll do it starting with C:
But there are some problems. The highest tone is a bit less than 7 octaves above the lowest tone! Their frequency ratio is called the Pythagorean comma. And we get a total of 13 tones, not 12.
To deal with these problems, we can simply omit one of these two tones and use only the other in our scale. There are two ways to do this, which are mirror images of each other:
Each breaks the symmetry of the scale. And each gives one fifth that's noticeably smaller than the rest. It's called a 'wolf fifth' — because it's so out of tune it howls like a wolf!
What can we do? One solution is simply to avoid playing this fifth. You've probably heard the old joke. A patient tells his doctor: "It hurts when I lift my arm like this." The doctor replies: "So don't lift your arm like that!"
This worked pretty well for medieval music, where the fifth and octaves were the dominant forms of harmony, and people didn't change keys much, so they could avoid the wolf fifth. But in the late 1300s, major thirds became very important in English music, and soon they spread throughout Europe. A major third sounds perfectly in tune — or technically, 'just' — when it has a frequency ratio of
$$ \displaystyle{ \frac{5}{4} = 1.25 } $$
But the major thirds in Pythagorean tuning are bigger than this!
Let's see why. This will eventually lead us to the solution called 'quarter-comma meantone' tuning.
To go up a major third in Pythagorean tuning, we take any tone and go up 4 fifths, getting a tone whose frequency is
$$ \displaystyle{ \left(\frac{3}{2}\right)^4 = \frac{81}{16} } $$
times as high. Then we go down 2 octaves to get a tone whose frequency is
$$ \displaystyle{ \frac{81}{64} = 1.265625 } $$
times that of our original tone. This is called a Pythagorean major third. It's close to the just major third, 5/4 = 1.25. But it's a bit too high!
Let's see what what these Pythagorean major thirds look like, and where they sit in the scale. To do this, let's take our original 'star of fifths':
and reorder the notes so they form a 'circle of fifths':
Here we see two wolf fifths, each containing one of the notes separated by a Pythagorean comma (namely G♭ and F♯). As we've seen, if we omit either one of these notes we're left with a single wolf fifth. But this breaks the left-right symmetry of the above picture, so let's leave them both in for now.
Now let's draw all the Pythagorean thirds in blue:
A pretty, symmetrical picture. But not every note has a blue arrow pointing out of it! The reason is that not every note has some other note in the scale a Pythagorean third higher than it. We could delve into this more....
But instead, let's figure out what to do about these annoyingly large Pythagorean thirds!
Historically, the first really popular solution was to use 'just intonation', a system based on simple fractions built from the numbers 2, 3 (as in Pythagorean tuning) but also 5. It was discussed by Ptolemy as far back as 150 AD. But it became widely used from roughly 1300 to at least 1550 — starting in England, and then spreading throughout Europe, along with the use of major thirds.
Just intonation makes a few important thirds in the scale be just, but not as many as possible. Around 1523 another solution was invented, with more just thirds: 'quarter-comma meantone'. It became popular around 1550, and it dominated Europe until about 1690. Let's see what this system is, and why it didn't catch on sooner.
The idea is to tweak Pythagorean tuning so that all the Pythagorean thirds I just showed you become just thirds! To do this, we'll simply take the Pythagorean system:
and shrink all the blue arrows so they have a frequency ratio of 5/4.
Unfortunately this will force us to shrink the black arrows, too, In other words, to make our major thirds just, we need to shrink our fifths. It turns out that we need fifths with a frequency ratio of
$$ \displaystyle{ \sqrt[4]{5} \approx 1.49534878\dots} $$
This is only a tiny bit less than the ideal fifth, namely 1.5. It's not a nasty wolf fifth: it sounds pretty good. In fact it's quite wonderful that the fourth root of 5 is so close to 3/2. So, using some fifths like this may count as an acceptable sacrifice if we want just major thirds.
Here's what we get:
This tuning system is called quarter-comma meantone.
You'll note that by shrinking the blue and black arrows — that is, the thirds and fifths — we've now made the note F♯ lower than G♭, rather than higher, as it was in Pythagorean tuning. Their frequency ratio is now $$ \displaystyle{ \frac{128}{125} = 1.024} $$
which is yet another of those annoying little glitches: this one is called the lesser diesis.
So that's quarter-comma meantone tuning in a nutshell. But there's a lot more to say about it. For example, I haven't explained all the numbers in that last picture. Where do \(\sqrt[4]{5}\) and the lesser diesis 128/125 come from??? I haven't even explained why this system called 'quarter-comma meantone'. These issues are related. I'll explain them both next time, but I'll give you a hint now. I told you that the Pythagorean major third $$ \displaystyle{ \frac{81}{64} = 1.265625 } $$ is a bit bigger than the just major third: $$ \displaystyle{ \frac{5}{4} = 1.25 } $$
But how much bigger? Their ratio is $$ \displaystyle{ \frac{81/64}{5/4} = \frac{81}{80} = 1.0125 } $$$ This number, yet another of those annoying glitches in harmony theory, is called the syntonic comma. And this, not the Pythagorean comma, is the comma that gives 'quarter-comma meantone' its name! By taking the syntonic comma and dividing it into four equal parts — or more precisely, taking its fourth root — we are led to quarter-comma meantone. I'll show you the details next time.
Quarter-comma meantone is dramatically different from the earlier tuning systems I've discussed, since it uses an irrational number: the fourth root of 5. I think this is why it took so long for quarter-comma meantone to be discovered. After all, irrational numbers were anathema in the old Pythagorean tradition relating harmony to mathematics.
It seems that quarter-comma meantone was discovered in a burst of more sophisticated mathematical music theory in Renaissance Italy — along with other meantone systems, but I'll explain what that means later. References to tuning systems that could be meantone appeared as early as the 1496 text Practicae musica by Franchinus Gaffurius. Pietro Aron unmistakably discussed quarter-comma meantone in Toscanello in musica in 1523. However, the first mathematically precise descriptions appeared in the late 16th century treatises by the great Gioseffo Zarlino (Le istitutioni harmoniche, 1558) and Francisco de Salinas (De musica libri septem, 1577). Those two also talked about 'third-comma' and 'two-sevenths-comma' meantone systems.
Quarter-Comma Meantone (Part 2)
Last time I introduced 'quarter-comma meantone', the tuning system shown above. Today let's see if we can understand all the numbers in this picture.
You see 13 circles with letters in them standing for tones in a scale, connected by arrows labeled by numbers. The numbers are the frequency ratios between these tones:
This is remarkably close to a 'just perfect fifth', with a frequency ratio of 3/2. We'd love to have a 12-tone scale with lots of just major thirds and just perfect fifths, but alas it's impossible!
Let's analyze what's going on with these three numbers by treating them as variables:
Here \(T\) stands for 'third' and it should be a number close to 5/4. \(F\) stands for 'fifth' and it should be close to 3/2. \(F\) should be close to 1.
If you look at the picture above you'll see one blue arrow takes you as far as four red arrows. You might naively think this implies \(T = F^4\) but that can't be true: for quarter-comma meantone we have \(F = \sqrt[4]{5}\) and \(T = 5/4\). So in fact
$$ \displaystyle{ T = \frac{F^4}{4} } $$
The point is that the notes in the picture represent not specific pitches but 'pitch classes': pitches modulo powers of 2. So, for example, you start at C and go up four fifths you get to E, but this E has frequency 4 times that of the E you get by going up a third from C.
Similarly, to go all the way around the circle you go along 12 red arrows and one purple arrow. You might naively think this means xF12 = 1. But in fact you've gone up 7 octaves: the frequency has gone up by a factor of 27. So in fact $$ x F^{12} = 2^7 $$ These are all the equations we need to get ourselves a scale: $$ F^4 = 4T, \qquad x F^{12} = 2^7 $$
We have 3 unknowns and just 2 equations, so we get a 1-parameter family of scales this way.
Delightfully, this family includes three of the most popular tuning systems in the last millennium of western music! They are the three most obvious choices: we can either take \(F = 3/2\), or \(T = 5/4\), or \(x = 1\)
This gives Pythagorean tuning! In this system \(x\) is actually less than 1. Its reciprocal is called the Pythagorean comma. I may sometimes call this \(p\): $$ \displaystyle{ p = \textrm{Pythagorean comma} = \frac{3^{12}}{2^{19}} = \frac{531441}{524288} \approx 1.0136 } $$ Since \(x\) is less than 1, the diminished fifth (G♭) is actually below the augmented fourth (F♯). This makes something funny happen if we write the notes so that the frequencies keep going up as we go clockwise. Ponder this:
If we love major thirds and want these to be just, we must take \(T = 5/4\). Then our equations force $$ \displaystyle{ T = \frac{5}{4}, \qquad F = \sqrt[5]{4}, \qquad x = \frac{2^7}{5^3} } $$
This gives quarter-comma meantone! Now \(x\) is greater than 1, and it's called the lesser diesis. I'll sometimes call it \(\delta\): $$ \delta = \textrm{lesser diesis} = 2^7/5^3 = \frac{128}{125} = 1.024 $$
Here's what quarter-comma meantone looks like:
If we want our augmented fourth to be the same as the diminished fifth, we must take \(x = 1\). Then our equations force $$ \displaystyle{ T = \sqrt[3]{2}, \qquad F = 2^{7/12}, \qquad x = 1 } $$
This gives 12-tone equal temperament:
This scale has more symmetry than the other two, but all the frequency ratios are irrational except for octaves.
Pythagorean tuning ruled western music, or at least western music theory, from at least 1000 to 1300 AD. Quarter-comma meantone was dominant from about 1550 to 1690. Equal temperament ruled from about 1790 to now. It's remarkable that they come from three different points on this algebraic curve: $$ F^4 = 4T, \qquad x F^{12} = 2^7 $$ It would be interesting to study this curve a bit more using ideas from algebraic geometry.
You'll notice two gaps in that chronology! Just intonation flourished from about 1300 to 1550, and this system was based on a different idea: trying to get as many frequency ratios as possible to be simple fractions. I've discussed it in detail starting here. A rich and interesting variety of 'well-tempered' systems competed from about 1690 to 1790; these tweak the idea of quarter-comma meantone in various ways, and I'll talk about them later. Can we describe them using points on some higher-dimensional algebraic variety — a 'moduli space' of tuning systems? That's a question I want to keep in mind.
I hope you understand the math underlying quarter-comma meantone a bit
better now. But I still haven't said why it's called 'quarter-comma
meantone'! For that we'll need to dig deeper into 'commas'. We'll
need to understand those well to appreciate the well-tempered systems.
Quarter-Comma Meantone (Part 3)
On December 13th I explained the tuning system shown above. But I didn't say why it's called 'quarter-comma meantone'.
Today I'll finally tell you what a 'quarter comma' is. Not only will this shed new light on this particular tuning system, it'll prepare you for understanding other meantone temperaments, like '1/3-comma', '1/6-comma' and so on.
As for the word 'meantone', that requires a whole other explanation. But one thing at a time!
We've already seen that there's a conflict built deep into the heart of music: a conflict between wanting lots of just perfect fifths, which are pairs of tones with frequency ratios of 3/2, and wanting lots of just major thirds, which are pairs of tones with frequency ratios of 5/4.
You can't have lots of both, though you can come close. The problem is that the fourth power of 3/2 is a bit more than 5: $$ \displaystyle{ \left( \frac{3}{2}\right)^4 = \frac{81}{16} = 5.0625 } $$
Their ratio is called the syntonic comma, and sometimes I'll call it \(\sigma\): $$ \sigma = \textrm{syntonic comma} = \frac{(3/2)^4}{5} = \frac{81}{80} = 1.0125 $$
As a result, going up 4 just perfect fifths is a bit more than going up a just major third and 2 octaves. The former increases the frequency by $$ \left( \frac{3}{2}\right)^4 = \frac{81}{16} = 5.0625 $$ while the latter increases it by $$ \frac{5}{4} \cdot 2^2 = \frac{80}{16} = 5 $$
The ratio of these is the syntonic comma.
In quarter-comma meantone, we make our perfect fifths a bit smaller to get our major thirds to be just. That is, we replace 3/2 by a slightly smaller number whose fourth power is exactly 5. Unsurprisingly, this number is none other than $$ \sqrt[4]{5} \approx 1.4953 $$ But here's another way to think about it: we take 3/2 and divide it by the fourth root of the syntonic comma! That way, when we raise the result to the fourth power, the syntonic comma cancels out the problem and we get exactly 5. So, I'm saying $$ \sqrt[4]{5} = \frac{3}{2} \sigma^{-1/4} $$
If this isn't obvious from what I've already said, do the math — it'll be good for you.
Musicians will say we've lowered our fifth by a quarter comma, since they implicitly take logarithms: when I say we're dividing by the fourth root of the syntonic comma, they say we're subtracting a quarter of a comma. I won't be talking that way, but I can still draw a picture of the quarter-comma meantone tuning system that shows these 'quarter commas':
Notice that we've got 12 of these quarter commas, one between every pair of notes except the devilish F♯ and G♭. That's a total of 3 commas. We can imagine systems where these 3 commas are distributed in other ways, and we'll be seeing a bunch of them soon, when we get to well-tempered tuning systems. What quarter-comma meantone does is spread out these commas as evenly as possible.
But what about those notes F♯ and G♭? As I've said before, we usually leave out one of those, to get a scale with 12 more or less equally spaced notes. Next time I'll show you what happens then.
Quarter-Comma Meantone (Part 4)
I've been talking about the marvelous tuning system that dominated western music from about 1550 to 1690: quarter-comma meantone. Above I've drawn it in its most mathematically beautiful form. For convenience I'm drawing it in the key of C, but you could use any key.
This scale has lots of 'just major thirds', which are pairs of notes with a frequency ratio of 5/4. I've drawn them as dark blue arrows.
This scale also has a visible symmetry under reflection across the vertical axis! What does this mean musically? It means that if you can reach some note in the scale by starting at C and multiplying the frequency by some number, you can reach some other note in the scale by starting at C and dividing by that number. Musicians call this symmetry 'inversion'.
Unfortunately this scale has 13 notes, not 12. But the real problem is not that 13 is an unlucky number. It's that two of the notes are absurdly close together! Their frequency ratio is a number very close to 1, called the 'lesser diesis': $$ \displaystyle{ \delta = \textrm{lesser diesis} = \frac{2^7}{5^3} = \frac{128}{125} = 1.024 } $$
So in practice, musicians usually leave out one of these two notes. This breaks the symmetry but gives a scale with 12 notes that are close to equally spaced.
Usually musicians leave out the higher of these two nearby notes, called the diminished fifth. When we're in the key of C, as above, this is the one called G♭. With G♭ removed, we're left with the following scale:
Now there's one fewer of those dark blue arrows: one just major third is gone. Also, our scale now has a 'wolf fifth' with frequency ratio audibly bigger than 1.5. So, we pay a price for breaking the symmetry and leaving out the diminished fifth.
Alternatively, we could leave out the lower of the two nearby notes, called the augmented fourth. This is the one called F♯. Then we get this scale:
It's just a reflected version of the scale above.
Is there any good reason to prefer the choice most people make, namely leaving out the diminished fifth? As a mathematician you might say "no, the two choices are related by a symmetry, so the choice we make is completely arbitrary". However, the symmetry we're talking about here — inversion symmetry, where we replace frequency ratios by their reciprocals — is not some god-given law of nature. After all, when you pluck a guitar string you hear an 'overtone series': not just the fundamental frequency but also the frequencies 2, 3, 4, etc. times that. You don't hear an 'undertone series' with frequencies 1/2, 1/3, 1/4 etc. times the fundamental!
People do try to do music with undertones, and it's fun — it's called 'negative harmony'. But undertones are physically not on an equal footing with overtones. And while a major triad and a minor triad are related by inversion symmetry, they sound very different. So there could be a reason to prefer the scale with an augmented fourth to the one with the diminished fifth. But I don't know it.
As I keep emphasizing, trying to create a nice tuning system is like trying to make your carpet look good when it's too big for your room. There are bound to be lumps in the carpet; all you can do is try to deal with them as best you can. You can try to spread them out evenly, try to gather them into one big lump and hide it under the couch, etc.
So, the math of tuning systems is the math of lumps. We can learn more about this by comparing quarter-comma meantone with Pythagorean tuning. Le's compare the versions that are missing the diminished fifth. We'll find a nice relation between three pesky numbers that are quite close to 1:
First let's take our quarter-comma meantone scale:
and write it using letter names for the lesser diesis and syntonic comma. I'll leave out the blue arrows, because we won't need them:
As we go all the way around this circle clockwise, the frequency goes up by 7 octaves. So, multiplying all the numbers labeling the arrows, we must have $$ \displaystyle{ \left( \frac{3}{2} \sigma^{-1/4} \right)^{12} \delta = 2^7 }. $$
As you can see, here the lumps in the carpet are the cube of the reciprocal of the syntonic comma, which we have smeared out over the whole circle of fifths, together with the lesser diesis, which we've concentrated in the wolf fifth.
On the other hand Pythagorean tuning is based on fact that going around this circle, we go up 7 octaves:
Mathematically this says $$ \displaystyle{ \left(\frac{3}{2}\right)^{12} p^{-1} = 2^7 }. $$
where \(p\) is the Pythagorean comma. So here the lump in the carpet is the reciprocal of the Pythagorean comma, which we've packed into the wolf fifth.
Putting these two equations together we see
$$ \displaystyle{ \sigma^{-3} \delta = p^{-1} } $$
or in other words $$ \displaystyle{ p \delta = \sigma^3}. $$
The Pythagorean comma times the lesser diesis is the syntonic comma cubed! Knowing this may help us later, when I discuss the fancier methods of dealing with lumps in the carpet used in well-tempered scales.
First, however, I want to explain that word 'meantone'. What's mean about the tones in quarter-comma meantone? I'll tell you next time!
Quarter-Comma Meantone (Part 5)
I've been talking about the quarter-comma meantone tuning system, which dominated western music from about 1550 to 1690. So far I've been drawing it using a circle of fifths, as above. This is a diagram where as we go clockwise each note is a fifth higher than the previous one.
But why is this system called 'meantone'? Briefly, it's because the size of a whole step between notes in this tuning system — called a 'tone' — is the geometric mean of the two kinds of whole step in Pythagorean tuning!
Let's figure this out. First we need to understand the frequency ratio of two neighboring notes separated by a half step, called a 'semitone'.
We can figure it out using pictures. Let's start by getting rid of the blue arrows for major thirds, which just clutter things up now:
Next, let's take this diagram and reorder the notes so they go up the chromatic scale: C, C♯, D, E♭, E, etc. This turns our circle of fifths into a 'star of fifths':
Now let's figure out the frequency ratios of neighboring notes! First, lets go up from C to C♯.
Follow the path from C to C♯ in the picture above. As you do, you'll go up 7 quarter-comma fifths, but you'll also hit the lesser diesis. Multiplying all these numbers you get $$ \displaystyle{ \frac{128}{125} \cdot 5^{7/4} = \frac{128}{5^{5/4}} \approx 17.12 }. $$ This is a lot bigger than 1, so you've gone up to some C♯ that lies octaves above our original C. You should divide by an appropriate power of 2 to get the C♯ right next to our original C. Namely, you should divide by 16. This gives $$ \displaystyle{ \frac{8}{5^{5/4}} \approx 1.06998}. $$
So this is how much you multiply the frequency of C to get the C♯ right above it! This number is called the quarter-comma diatonic semitone.
Next, let's go up from C♯ to D.
With your finger or eye, follow the path from C♯ to D:
As you do, you go up 7 quarter-comma fifths — and this time, you don't hit the lesser diesis! So this time the numbers along the path multiply to $$ \displaystyle{ 5^{7/4} \approx 16.72}. $$ Again we need to divide by 16, getting $$ \displaystyle{ \frac{5^{7/4}}{16} \approx 1.04491}. $$
So this is how much we multiply the frequency of C♯ to get the D right next to it. This number is called the quarter-comma chromatic semitone.
If you go through all the notes of the scale you'll see they're all spaced by diatonic or chromatic semitones... with one exception, namely the tiny space between F♯ and G♭, which is just the lesser diesis.
Indeed, we get this pattern of semitones:
To see it better, we can remove the scaffolding of fifths:
By the way, since the diatonic semitone includes the lesser diesis while the chromatic semitone does not, we get this relation:
Okay, but what does all this have to do with the term 'meantone'? Well, in music a 'tone' is two semitones. Since the semitones in quarter-comma meantone generally alternate between diatonic and chromatic, a tone is usually equal to
Fans of the golden ratio will notice that this number is 1/2 less than that!
But the name 'meantone' arises because this number \(\sqrt{5}/2\) is the geometric mean of the two kinds of tones in just intonation, namely 9/8 and 10/9: $$ \sqrt{\frac{9}{8} \cdot \frac{10}{9}} = \frac{\sqrt{5}}{2}. $$
While the tones in just intonation hop back and forth between the larger 9/8 and the smaller 10/9, in quarter-comma meantone they generally stay at the mean of those two... which you might even call the golden mean!
Quarter-Comma Meantone (Part 6)
So far I've focused on the quarter-comma meantone system in its mathematically beautiful, symmetrical form above. Today I'll say more about the scale as actually played: how we trim it down from a 13-note scale to a more practical 12-note scale, and what are the intervals between notes in the resulting scale.
The scale above has:
You can see this tiny gap between F♯ and G♭. Both these notes are versions of the 'tritone' in the scale of C major. F♯ is called the 'augmented fourth' and G♭ is called the 'diminished fifth'. Unless we build a keyboard with split keys — as some people actually have, but they never caught on — one of these notes has got to go!
There are two options. The most popular is to remove the diminished fifth:
The other is to remove the augmented fourth:
Either approach gives a big bad 'wolf fifth', which must be avoided. But what does the resulting scale actually look like? What are the intervals between neighboring notes?
To understand this let's go back to the start, our original 'circle of fifths' with 13 notes:
When we rearrange the notes, listing them in order, we get a 'star of fifths':
Now let's add arrows showing the intervals between neighboring notes:
Except for the lesser diesis, the neighboring notes are all separated by two kinds of interval:
We worked out these wacky numbers in my December 31st diary entry. It may seem weird to have two sizes of semitone, but they sound fine. The problem, to repeat myself, is the lesser diesis between the augmented 4th and the diminished 5th. But when we remove either one of these notes, something nice happens!
This is the cool part. On December 31st we saw this relation:
So, when we remove either the augmented 4th or diminished 5th, the lesser diesis combines with one of the chromatic semitones adjacent to it to give an extra diatonic semitone!
If we remove the diminished 5th, we get this scale:
It's not completely symmetrical, but it's still quite pretty — and now the lesser diesis has been banished. Most of the fifths sound good, but there's wolf fifth between the augmented fourth (F♯) and the minor second (C♯), so you should avoid this. The semitones alternate between chromatic and diatonic... except for two diatonic semitones in a row between F♯ and A♭, and between B and C♯.
Best of all, this scale has lots of just major thirds — though one fewer than in the mathematically beautiful 13-note version of the scale. Let's figure out where they are. Last time we noticed this relation:
This implies that
But 5/4 is the frequency ratio of a just major third! So we get a just major third whenever we go up two chromatic semitones and two diatonic semitones. So the just major thirds are the blue arrows here:
It's a bit random-looking, thanks to how we broke the symmetry. If there were a just major third from F♯ to B♭ the pattern of blue arrows would be symmetrical. But there's not: there's only a just major third from G♭ to B♭, and we've eliminated G♭ from this scale.
But still, this scale has lots of just major thirds! And that was the main goal.
Quarter-Comma Meantone (Part 7)
I've said a lot about quarter-comma meantone and its great properties. It's almost time to start exploring the vast realm of 'well-tempered' tuning systems that flourished starting around 1690.
But there's one more thing I want to say about quarter-comma meantone. If you use this system, there are some advantages to having your scale start at D rather than C! For example, Wikipedia presents quarter-comma meantone starting from D here:
It's not an arbitrary decision! This confused me at first, but Matt McIrvin straightened me out and I think I get it now. It's all about white keys versus black keys on the piano — or harpsichord, or clavichord, or organ.
The same ideas also apply to Pythagorean tuning or just intonation, but I'll illustrate them with quarter-comma meantone.
If we straighten out the circle of fifths shown above, putting C at the middle, we get this picture:
There are 13 notes here, since we need an odd number of notes if we want one to be in the middle. Thus, I'm writing F♯ and G♭ as two separate notes, even though some tuning systems consider them as the same. Of course in the picture at the top of this blog article they were different.
Notice how asymmetrical this picture is. To emphasize the asymmetry I've marked the flat notes in red and the sharp ones in blue. Though C is in the middle, it's much closer to the flat notes than the sharp ones!
You may complain that any flat note can be rewritten as a sharp one. That's true. So here's a more precise way to make my point. Say a note is an accidental if it has either a flat sign or a sharp sign. Then: though C is in the middle, there are more accidentals to its left than to its right!
But here's the weird part. If we straighten out the circle of fifths putting D at the middle, this asymmetry evaporates:
Puzzle. Why is this true? Why, even though the white notes on a piano form a major scale starting at C, does
equal
only when you start at D?
Of course a 'why' question can have many different answers, including that's just how things are! But there are a few enlightening answers to this question. I'll just mention that I'm not concerned here with our conventions concerning letter names for notes.
Yes, it's odd that we say the white notes on a piano form a major scale starting with C rather than something more logical like A. That convention ultimately goes back to a decision made by Boethius shortly after 500 AD, long before pianos or harpsichords existed:
But if we changed our letter names for notes, my puzzle would persist, with different names for things.
Now to the point. All along in my discussion of quarter-comma meantone I've started my scales at C. This puts all the problems connected to the tritone at the bottom of this circle, between F♯ and G♭:
But there are more accidentals on the left side of this circle than on the right! There are five on the left and just one on the right.
If instead we start our scale at D, this asymmetry disappears:
Now we've got 3 flat notes on the left of the circle and 3 sharps on the right.
This has implications for practical music. Basically, we'd like to hide the lesser diesis 128/125, or the wolf fifth that appears when we eliminate the lesser diesis, as deeply as possible among the black notes. That will make the scales that are mainly white notes sound better.
Even if you haven't followed all the details, I hope you've seen that there's a lot of richness to the tuning systems I've discussed so far. They kept musicians happy until around 1690. But then a large number of 'well-tempered' systems burst onto the scene, which exploited the basic principles we've seen so far in new ways. So that's what I want to talk about next!
The tuning system called 'quarter-comma meantone’ dominated western keyboard music from about 1550 to roughly 1690. The reason: it has very nice thirds and fifths in many different keys!
But as I keep saying, every tuning system has problems: like lumps in the carpet, the best you can do is move the problems around. Quarter-comma meantone achieves its greatness by completely flattening out the carpet except for one big lump: a single highly dissonant 'wolf fifth'. Alas, this utterly spoils keys where that fifth is important — or other chords using the note that creates that wolf fifth, which is F♯ in the chart above.
As Baroque musicians became increasingly interested in switching between keys, there was pressure to find tuning systems where the lumps in the carpet were more evenly spread out. But interestingly, they did not embrace equal temperament, where the lumps are spread out as evenly as possible.
It's not that equal temperament was unknown! Apparently, musicians wanted some keys to have truly beautiful fifths and thirds, and weren't willing to sacrifice that beauty and purity to make all keys sound equally good — or bad. Thus, they invented compromise systems, called well temperaments, in which each key has its own personality, but all sound reasonably good.
You can see these personalities discussed in Christian Schubart's Ideen zu einer Aesthetik der Tonkunst, written in 1806:
C Major. Completely pure. Its character is: innocence, simplicity, naïvety, children's talk.C Minor. Declaration of love and at the same time the lament of unhappy love. All languishing, longing, sighing of the love-sick soul lies in this key.
D♭ Major. A leering key, degenerating into grief and rapture. It cannot laugh, but it can smile; it cannot howl, but it can at least grimace its crying. Consequently, only unusual characters and feelings can be brought out in this key.
C# Minor. Penitential lamentation, intimate conversation with God, the friend and help-meet of life; sighs of disappointed friendship and love lie in its radius.
D Major. The key of triumph, of Hallejuahs, of war-cries, of victory-rejoicing. Thus, the inviting symphonies, the marches, holiday songs and heaven-rejoicing choruses are set in this key.
It's with great effort that I resist listing all 24 keys! You'll just have to visit the link to see which key "tugs at passion as a dog biting a dress", and which has "pious womanliness and tenderness of character".
When equal temperament took over in the early 1800s, all this diversity was flattened, although the reputations of the different keys persisted for quite some time. Some consider this flattening a tragedy; others say it opened the doors to Beethoven and jazz. Perhaps both are true.
But what were these well tempered systems, exactly? What were their distinct advantages? Here things get much more complicated and murky. For example:
The biggest advertisement for well-tempered tuning systems was Bach's The Well-Tempered Clavier. In 1722 and then again in 1742, he wrote a piece in each of the 12 major and 12 minor keys, to illustrate the flexibility of well temperament — and presumably to showcase how different keys had different personalities. But which well tempered system was he actually using?
Nobody knows! We don't have Bach's words on this topic, and despite a vast amount of scholarship nobody has been able to pin it down. Serious musicologists have even spent serious time studying a doodle in Bach's manuscript of The Well-Tempered Clavier, hoping it contains an encoded description of his tuning system! There's no proof that it does.
For a fun but insightful introduction to the controversy, watch this:
For more, try this:
This seems to be the best in-depth survey of the subject:
I haven't read most of it, but it looks to be a treasure chest of information on well temperaments, their history and their mathematics. And frankly, I find that much more interesting than the futile quest to figure out what Bach was thinking.
There are a lot of interesting well tempered systems. People wrote a lot about them when they were invented, and much more since. So we are not reduced to decoding Bach's squiggles to understand well temperaments. The hard part, at least for this mathematician, is figuring out their governing principles.
In my efforts, I've been helped immensely by this website:
He describes about 30 different tuning systems using circular diagrams — a method that I've decided to copy in my blog articles here. He is less interested in the math than I am. But he is more more efficient at explaining tuning systems than other sources, and covers other topics: for example, he describes how to tune a harpsichord in all these systems!
Instead of covering well-tempered systems chronologically, I'll start with the ones I find easiest to explain. I'll try to cover some of the most important ones, but certainly not all. Many are named after people like Werckmeister, Kirnberger and Vallotti, while some have descriptive names like sixth-comma meantone.
The danger is getting lost in the undergrowth of these tuning systems and not seeing the forest for the trees. So before diving in, I'll start by surveying some of the mathematical principles that seem to be at work. You could see these between the lines of what I've written so far, but I want to be a bit more explicit.
For example, what's really going on with these weird numbers:
and this relationship:
Why have these funny things mattered so much in the history of tuning systems?
If all the frequency ratios in our tuning system were powers of 2:
life would be very simple. Multiplying a frequency by 2 raises its pitch by an octave, so the only chords we could play are those built out of octaves. Not much music could be made! But there'd be no difficult decisions, either.
In Pythagorean tuning, also called 3-limit tuning, we generate all our frequency ratios by multiplying powers of 2 and powers of 3:
This is more exciting. While the frequency ratio of 2 is an octave, that of 3/2 is called a just perfect fifth. So now we can use octaves and fifths to build other intervals (that is, frequency ratios).
But in fact, any positive real number can be approximated arbitrarily well by numbers of the form 2i · 3j, so we have an embarrassment of riches: more intervals than we really want! To bring the system under control, we take some number of the form 2i · 3j that's really close to 1 and act like it is 1.
I examined the options in an earlier post and got a list of 'winners' according to some precise criterion. A couple of early winners are
and
These would be important in scales with 5 or 7 notes, but western music holds out for a much better one, called the Pythagorean comma:
This is important for a 12-tone scale, because it means that if we go up 12 fifths, multiplying the frequency by 3/2 each time, it's almost the same as going up 7 octaves.
But not quite! There are many ways of dealing with this problem. In Pythagorean tuning we absorb the problem by dividing one of our fifths by the Pythagorean comma, turning it into an unpleasant 'wolf fifth':
For example:
But we can spread the inverse of the Pythagorean comma around the circle of fifths any way we like, and different ways give different tuning systems.
For example, in equal temperament we spread it completely evenly around the circle of fifths, using the equal tempered fifth everywhere:
This is not an example of 3-limit tuning because it uses irrational numbers! But it's an obvious way to solve the problem of the Pythagorean comma which emerges in 3-limit tuning. More interesting solutions tend to involve the next prime number.
In 5-limit tuning we generate all our frequency ratios by multiplying powers of 2, 3 and 5:
Equivalently, we build them using the octave (2), the just perfect fifth (3/2) and the just major third: 5/4.
There are some new simple fractions close to 1 that you can build with 2, 3 and also 5. The most important is the syntonic comma:
This shows up when you try to reconcile the perfect fifth and the major third. If you go up four just perfect fifths, you boost the frequency by a factor of (3/2)4 = 81/16 = 5.0625, which is a bit more than a major third and two octaves, namely 5/4 × 22 = 5. The ratio is the syntonic comma.
As we'll see in future episodes, this realization is fundamental to many well tempered tuning systems. We've already seen the grand-daddy of these systems: quarter-comma meantone. It's not well tempered itself, but fixing its main flaw leads to well tempered systems. In quarter-comma meantone, we divide most of our fifths by the fourth root of the syntonic comma, which gives lots of just major thirds, shown in blue below:
So, this scale has many 'quarter-comma fifths' with a frequency ratio of (3/2)σ-1/4. Going around the whole circle and multiplying 12 of these quarter-comma fifths would give 125, which is not quite the 128 we need to go up 7 octaves. So we need to take one of these quarter-comma fifths and multiply it by 128/125. The resulting 'wolf fifth' sounds terrible — and this is what well temperaments seek to cure.
The number 128/125 is an important fraction close to 1 built from just the primes 2 and 5. It's called the lesser diesis:
It's not only a power of 2 divided by a power of 5, but also a power of 2 divided by a power of 10. You've bumped into it if you've ever wondered why people often use 'kilobyte' to mean 1024 bytes, not 1000.
From the Pythagorean comma, syntonic comma and lesser diesis we can generate other fractions close to 1 built from the primes 2, 3 and 5. For example, I've already discussed the product of the syntonic comma and lesser diesis, and also their ratio.
But when we study well temperaments, more important will be the Pythagorean comma divided by the syntonic comma. Called the schisma, this fraction is very close to 1:
I'll talk about it more next time.
It's also important to note that the lesser diesis is not independent from the Pythagorean comma and syntonic comma. We've already seen today that going up a fifth twelve times is the same as going up 7 octaves divided by the Pythagorean comma. Now we're seeing that going up (3/2)σ-1/4 twelve times is the same as going up 7 octaves times the lesser diesis. So, we have
or
We've already this in a slightly different way before.
Due to this relation there must be other fractions close to 1, built only from powers of the primes 2, 3, and 5, that are independent from p, σ and δ. In fact, we've already seen four such fractions appearing as the sizes of semitones in just intonation:
The ratios of these semitones include the syntonic comma, the lesser diesis, and also their product the greater diesis and their ratio the diaschisma!
But these semitones are not extremely close to 1. The smallest, the lesser chromatic semitone, is 25/24 ≈ 1.041666. So there must be interesting examples of fractions built from 2, 3 and 5, independent of the syntonic and Pythagorean commas, and much closer to 1. On Mastodon I asked for examples built solely from the primes 3 and 5, and a bunch of people helped me out. Here are some of the first few winners:
The main thing to notice here is that we need fractions with impractically large numerators and denominators to get closer than the large diatonic semitone, 27/25 = 1.08. These fractions won't play a role in well temperaments.
I won't say much about primes after 5 now. But they've been studied in music theory at least since Ptolemy, and the compositions of Ben Johnston really run wild with them. For a tiny bit about the virtues of the prime 7, read my post on the harmonic seventh chord.
The facts I've crudely laid out above must be part of an elegant general theory of approximating the number 1 by fractions built from powers of a specified set of primes, and how to build scales from these fractions. Done systematically, this could be of interest not just to music theorists but even pure mathematicians. But I will not explore this now, since my goal was merely to recall some facts needed to understand the explosion of well temperaments starting around 1690!
Next time I'll digress slightly into Kirnberger's discovery of a tuning system with frequency ratios built only from the primes 2, 3, and 5 that comes extremely close to equal temperament. This is not a practical system, but it relies on an utterly astounding coincidence, and more importantly it highlights the role of the schisma, which will keep showing up in other systems.
It was discovered by Bach's student Johann Kirnberger, and it has a frequency ratio absurdly close to 1:
It arose naturally in Kirnberger's attempt to find a tuning system close to equal temperament with only rational frequency ratios. But it relies on a mathematical miracle: a coincidence so eye-popping that a famous expert in black hole physics wrote a paper trying to explain it!
Throughout my discussion of tuning systems, we've repeatedly encountered two glitches in the fabric of music called 'commas':
The first shows up when you try to build a scale from fifths, while the second shows up when you try to have lots of nice fifths and major thirds.
They are quite close together, so their ratio is even closer to one! It has a cool name: it's called the schisma. I'll abbreviate it with the Greek letter chi:
The schisma is a kind of meta-glitch: a glitch between glitches! It may seem like a mere curiosity, since two pitches whose frequency ratio is a schisma sound the same to everyone. But precisely for this reason, it plays a role in some well tempered tuning systems.
You see, sometimes when you're building a tuning system you need a Pythagorean comma to make your circle of fifths close up nicely, but to get a really nice major third you use the syntonic comma instead. When you do this, you're off by a schisma! And like a lump in the carpet, this schisma has to go somewhere. It's so small that it scarcely matters where you put it. If you're not extremely careful in tuning, your notes are probably off by more than a schisma anyway. But mathematically, it's there.
In future episodes, I'll show you examples of how this happens in some well-known tuning systems. But today I want to show you a mind-bending, completely crazy way that Kirnberger used the schisma.
Let's get started!
As we saw in our study of Pythagorean tuning, going up 12 just perfect fifths takes you up a bit more than 7 octaves. Their ratio is the Pythagorean comma:
As a result, if we divide the just perfect fifth (that is, 3/2) by the 12th root of the Pythagorean comma, we get the equal tempered fifth (that is, 27/12), whose 12th power is exactly 7 octaves. This correction, the 12th root of the Pythagorean comma,
is called a grad. I'll call it γ for short:
So, what I'm saying is that if we divide 3/2 by the grad we get 27/12, which is the equal tempered fifth:
Now for the eye-popping coincidence. The grad
is remarkably close to the schisma:
Look at that! For no obvious reason, they match to almost seven decimal places! 
But unlike the grad, the schisma is rational. This let Kirnberger create a tuning system very close to equal temperament but with rational frequency ratios. His idea was to use a circle of fifths where instead of using the equal tempered fifth
which is irrational, we use 3/2 divided by a schisma
which is rational. They are remarkably close!
The quantity 3/2χ is called the schismatic fifth:
We can try to build a circle of fifths using the schismatic fifth instead of the equal-tempered fifth. But there's a slight problem. Actually, 'slight' is an overstatement: it's a nearly infinitesimal problem.
If we go up 12 schismatic fifths we don't go up exactly 7 octaves. We go up a microscopic amount more, since
and the number (γ/χ)12 is microscopically more than one. Since this number was discussed by Kirnberger, it's called the atom of Kirnberger. I'll call it α for short:
Let's work out what it equals! Remember that the grad is the 12th root of the Pythagorean comma, so
and turning the crank on the old calculator:
Using these ideas, Kirnberger created a tuning system called rational equal temperament. It's very close to equal temperament, but with only rational numbers as frequency ratios. To do this, he used 11 schismatic fifths and one schismatic fifth divided by the atom of Kirnberger. Just for fun, I'll call the last an atomic fifth:
I don't know where Kirnberger put the atomic fifth, but I'll follow the common tradition of putting problems right after the tritone, which is F♯ in the key of C:
Compare this to equal temperament:
Nobody can hear the difference, so Kirnberger's rational equal temperament is not used in music. But it sheds light on the interaction between the Pythagorean comma and syntonic comma, and that is important for the well tempered scales we'll be seeing next.
It also raises a math puzzle: why is the grad so close to the schisma? The physicist Don Page, famous for his work on black hole thermodynamics, has written a paper exploring this:
Since the schisma is already a meta-glitch, the Kirnberger kernel is a meta-meta-glitch! He shows that the closeness of this number to 1 is equivalent to a number of other coincidences, notably
He then wrestles this coincidence down to a fact involving only integers, which he tries to explain using properties of the hyperbolic tangent function! He is much better at these things than me, so if you enjoyed my article you should definitely take a look at his.
Next time I'll get back to business and talk about well tempered tuning systems — starting with three more practical systems developed by Kirnberger.
Now I want to start talking about some important well-tempered tuning systems invented by Johann Philipp Kirnberger. But first: who was this guy? As I tried to answer this question for myself I became sort of fascinated with his personality.
Kirnberger was a German music theorist who played an important role in formalizing baroque harmony and counterpoint. He was born in 1721.
As a child he studied the violin and harpsichord at home. He then moved to another town to study the organ, and then at 17 moved again to start seriously studying the violin. At the age of 18, he went to Leipzig to study performance and composition with Johann Sebastian Bach. He did this intermittently for three years, but this seems to have been a pivotal period in his life. Bach was an energetic teacher, with about 300 students over his life, but unfortunately he never wrote down his thoughts on music. In the end, it largely fell to Kirnberger to systematize Bach's ideas on harmony and composition.
Between the ages of 20 and and 30, Kirnberger worked in Poland and wrote a book on Polish dances. He then became a violinist at the court of Frederick II of Prussia, and from the age of 37 until his death at the age of 61 he was music director for the princess of Prussia.
But most of all, Kirnberger was a big fan of Bach. He called Bach "the greatest of all composers." Around the age of 40 he published a book of Bach's clavier pieces, and he worked hard to publish all of Bach's chorales, which finally appeared after Kirnberger's death. He preserved many of Bach's manuscripts in his library. He even wrote some pieces that for a while were attributed to either J. S. Bach or C.P.E. Bach — like this concerto for harpsichord, written when Kirnberger was about 50:
Kirnberger was better as a music theorist than a performer — though as a theorist he was quite polemical. In 1794, ten years after Kirnberger's death, a musician named Friedrich Nicolai wrote:
Kirnberger has many good musical ideas [...] he deserves full credit as a theorist. But he is unable to bring any of his ideas to good musical fruition, perhaps because of insufficient ability. His aim is not to see good music performed, but merely to find music containing "errors" so that he may make learned-and often violent-statements about others' mistakes. As a performer he has practically no skill at all, except when playing his own compositions; his sense of rhythm is especially uncertain.
His frustrations seem to have driven him to mathematics. When Kirnberger was 52, Charles Burney wrote that he
is said to be soured by opposition and disappointment; his present inclination leads him to mathematical studies, and to the theory of music, more than the practice [...] In his late writings, he appears to be more ambitious of the character of an algebraist, than of a musician of genius.
His discovery of the 'atom of Kirnberger', which I explained on January 18th, indeed seems like something only a person with a strong mathematical bent could do!
His three-part theoretical work Die Kunst des reinen Satzes in der Musik, or The Art of Strict Musical Composition, had a big impact in his day. However, he wrote poorly. Nicolai wrote:
Kirnberger considered himself to be a philosophical musician. In reality, he had pondered over his art more than other musicians. For all that, he did not have clear concepts about so many things, still less philosophically correct ones. Because he had no formal education at all and had read little, he lacked much necessary knowledge, which he could acquire only by considerable effort through association with scholars; therefore, he sometimes could not explain rather ordinary things clearly. Scholars who wanted to come to an understanding with him had to divine his meaning.
In fact, parts of Die Kunst des reinen Satzes in der Musik were actually written by a student of Kirnberger's who could write more clearly. This student, Johann Abraham Peter Schulz, said as much:
I had just recently made a systematic reduction of his [Kirnberger's] principles of harmony for my own benefit and satisfaction. And at his request I had applied this system practically to the analysis of two pieces by Joh. Seb. Bach, which are difficult to understand [...] His student's writing pleased the teacher and he permitted it to be published under his name.
That could get someone in trouble today.
Kirnberger was an argumentative man. He was quite harsh in his condemnation of two other important theorists, Rameau and Marpurg. In 1800, a fellow named Reichart wrote:
Kirnberger was a very passionate man who gave himself up to his impetuous temperament [...] The cultivation of his art, as he saw it and believed to embrace it, went before everything. The few righteous musicians whom he acknowledged possessed him completely and absorbed his entire disposition. Everything that did not immediately further the higher part of the art [...] he despised and considered repugnant.
All in all, a curious and interesting character.
As I discussed on January 11th, in a 'well temperament' each key gives a scale with its own different flavor. Quite a number of well temperaments had been used since Andreas Werckmeister invented three of them starting in 1681. (I'll explain those later.) By the time Kirnberger got involved, equal temperament was beginning to take over. In fact in 1760, at the age of 39, he published something called Construction der gleichschwebende Temperatur, about the construction of equal temperament. But in Die Kunst des reinen Satzes in der Musik he explained that he didn't like equal temperament, because it reduced the diversity of scales down to just two: major and minor. And in a letter 19 years later, he wrote:
Equal temperament is absolutely terrible, only being useful in the case of properly positioning the frets of a theorbo, lute or other such similar instrument such as a psaltry, zither etc., as a temperament of another type does not do each string justice.
Today, Kirnberger is mainly known for two well-temperaments called Kirnberger II and Kirnberger III. But he seems to have put work into a least two more tuning systems. First, unsurprisingly, there's his well temperament called Kirnberger I. Second, there is 'rational equal temperament' — a system I explained on January 18th. But this is so close to 12-tone equal temperament that nobody can hear the difference: its only advantage, if you can call it that, is having frequency ratios that are rational numbers — with, unfortunately, rather huge numerators and denominators. I doubt anyone has actually used it, except perhaps as an experiment.
What are Kirnberger I, II and III actually like?
First, as a point of comparison, recall the tuning system that all well-tempered systems are responses to. Namely, quarter-comma meantone:
This system has a lot of fifths that have been lowered by a quarter comma: that is, divided by σ1/4 where σ is the syntonic comma. These 'quarter-comma fifths' are just slightly smaller than the 'just' perfect fifth, namely 3/2. So that's good. It has a lot of 'just' major thirds, with frequency ratios of exactly 5/4, shown as the blue arrows above. So that's great. But to pay the price for all those quarter-comma fifth, it has a 'wolf fifth' that's 128/125 times bigger than all the rest. And that's noticeably ugly!
Well-tempered fifths seek to kill the wolf. Here's how Kirnberger I does it:
Here's Kirnberger II:
And here's Kirnberger III:
Puzzle. Do you see the pattern?
I'll examine these systems in more detail next time.
The quote of Kirnberger saying equal temperament is absolutely terrible comes from here:
It originated in a letter from Kirnberger to someone named Forkel, written around 1779.
I got all my other quotes from here:
Notes is a nice name for a music journal! This article is about Kirnberger and his student Schulz, analyzing how much each might have contributed to the writing of Die Kunst des reinen Satzes in der Musik and also the encyclopedia Allgemeine Theorie der schonen Kunste (General Theory of the Fine Arts). To help figure this out, Jerold investigates Kirnberger's views and personality.
Okay, let's study Kirnberger's three well-tempered tuning systems! I introduced them last time, but now I've developed a new method for drawing tuning systems, which should help us understand them better.
As we saw on January 15th, tuning theory involves two numbers close to 1, called the Pythagorean comma (≈ 1.0136) and the syntonic comma (= 1.0125). While they're not equal, they're so close that practical musicians often don't bother to distinguish them! They call both a comma.
So, my new drawing style won't distinguish the two kinds of comma.
Being a mathematician, I would like to say a lot about why we can get away with this. But that would tend to undercut my claim that the relaxed approach makes things simpler! I don't want to be like the teacher who prefaces the explanation of a cute labor-saving trick with a long and confusing theoretical discussion of when it's justified. So let me start by just diving in and using this new approach.
First I'll illustrate this new approach with some tuning systems I've already discussed. Then I'll show you Kirnberger's three well-tempered systems. At that point you should be in a good position to make up your own well temperaments!
Here is Pythagorean tuning in my new drawing style:
The circle here is the circle of fifths. Most of these fifths are black arrows labeled by +0. These go between notes that have a frequency ratio of exactly 3/2. This frequency ratio gives the nicest sounding fifth: the Pythagorean fifth.
But one arrow on the circle is red, and labeled by -1. This fifth is one comma flat compared to a Pythagorean fifth. In other words, the frequency ratio of this fifth is 3/2 divided by a comma. This arrow is red because it's flat — and it's a fairly bright red because one comma flat is actually quite a lot: this fifth sounds pretty bad!
(The comma here is a Pythagorean comma, but never mind.)
This illustrates a rule that holds for every tuning system we'll consider:
Rule 1. The numbers labeling arrows on the circle of fifths must sum to -1.
Now let's look at Pythagorean tuning again, this time focusing on the arrows inside the circle of fifths:
The arrows inside the circle are major thirds. A few of them are black and labeled +0. These go between notes that have a frequency ratio of exactly 5/4. That's the nicest sounding major third: the just major third.
But a some the arrows inside the circle are green, and labeled by +1. These major thirds are one comma sharp compared to the just major third. In other words, the frequency ratio between notes connected by these arrows is 5/4 times a comma. These arrows are green because they're sharp — and it's a fairly bright green because one comma sharp is actually quite a lot.
(These commas are syntonic commas, but never mind.)
Why do the major thirds work this way? It's forced by the other rule governing all the tuning systems we'll talk about:
Rule 2. The sum of the numbers labeling arrows for any four consecutive fifths, plus 1, equals the number labeling the arrow for the corresponding major third.
This rule creates an inherent tension in tuning systems! To get major thirds that sound really nice, not too sharp, we need some fifths to be flat. Pythagorean tuning is one way this tension can play out.
Now let's look at another tuning system: equal temperament.
Pythagorean tuning had eleven fifths that are exactly right, and one that's 1 comma flat. The flatness was as concentrated as possible! Equal temperament takes the opposite approach: the flatness is spread out equally among all twelve fifths. Rule 1 must still hold: the total flatness of all the fifths is still 1 comma. So each fifth is 1/12 of a comma flat.
How does this affect the major thirds? Rule 2 says that each major third must be 2/3 of a comma sharp, since
My pictures follow some color rules that are too boring to explain in detail, but bright colors indicate danger: intervals that are extremely flat or extremely sharp. In equal temperament the fifths are all reddish because they're all flat — but it's a very dark red, almost black, because they're only slightly flat. The major thirds are fairly sharp, so their blue-green color is more noticeable.
Now let's look at another important tuning system: quarter-comma meantone. This system was very popular from 1550 until around 1690. Then people started inventing well temperaments as a reaction to its defects. So we need to understand it well.
Here it is:
All but one of the fifths are slightly flat: 1/4 comma flat. This is done to create a lot of just major thirds, since Rule 2 says
This is the beauty of quarter-comma meantone! But it's obtained at a heavy cost, as we can see from the glaring fluorescent green.
Because 11 of the fifths are 1/4 comma flat, the remaining one must be a whopping 7/4 commas sharp, by Rule 1:
This is the famous 'wolf fifth'. And by Rule 2, this wolf fifth makes the major thirds near it 2 commas sharp, since
In my picture I wrote '8/4' instead of 2 because I felt like keeping track of quarter commas.
The colors in the picture should vividly convey the 'extreme' nature of quarter-comma meantone. As long as you restrict yourself to playing the dark red fifths and black major thirds, it sounds magnificently sweet. But as soon as you enter the fluorescent green region, it sounds wretched! Well temperaments were created to smooth this system down... without going all the way to the bland homogeneity of equal temperament.
And now let's look at Kirnberger's three well tempered systems. Only the third was considered successful, and we'll see why.
Here is Kirnberger I:
The flatness of the fifths is concentrated in a single fifth, just as in Pythagorean tuning. Indeed, from this picture Kirnberger I looks just like a rotated version of Pythagorean tuning! That's a bit deceptive, because in Kirnberger I the flat fifth is flat by a syntonic rather than a Pythagorean comma. But this is precisely the sort of nuance my new drawing style ignores. And that's okay, because the difference between the syntonic and Pythagorean comma is inaudible.
So the only noticeable difference between Kirnberger I and Pythagorean tuning is the location of flat fifth. And it's hard to see any advantage of putting it so close to C as Kirnberger did, rather than putting it as far away as possible.
Thus, it's not so suprising that I've never heard of anyone actually using Kirnberger I. Indeed it's rare to even see a description of it: it's very obscure compared to Kirnberger II and Kirnberger III. Luckily it's on Wikipedia:
Here is Kirnberger's second attempt:
This time instead of a single fifth that's 1 comma flat, he used two fifths that are 1/2 comma flat.
As a result, only 3 major thirds are just, as compared to 4 in Kirnberger II. But the number of major thirds that are 1 comma sharp has gone down from 8 to 7. The are also 2 major thirds that are 1/2 comma sharp — the bluish ones. So, this system is less 'extreme' than Kirnberger I: the pain of sharp major thirds is more evenly distributed. As a result, this system was more widely used. But it was never as popular as Kirnberger III.
For more, see:
This time instead of a two fifths that are 1/2 comma flat, he used four fifths that are 1/4 comma flat! A very systematic fellow.
This system has only one just major third. It has 2 that are 1/4 comma sharp, 2 that are 2/4 comma sharp, 2 that are 3/4 comma sharp, and only 3 that are 1 comma sharp. So it's noticeably less 'extreme' than Kirnberger II: fewer thirds that are just, but also fewer that are painfully sharp.
I think you really need to stare at the picture for a while, and think about how Rule 2 plays out, to see the beauty of Kirnberger III. But the patterns become a bit more visible if we rotate this tuning system to give it bilateral symmetry across the vertical axis, and write the numbers in a symmetrical way too:
Rotating a tuning system just means we're starting it at a different note — 'transposing' it, in music terminology.
The harpsichord tuning expert Cary Beebe writes:
One of the easiest—and most practical—temperaments to set dates from 1779 and is known as Kirnberger III. For a while, some people thought that this might be Bach’s temperament, seeing as Johann Philipp Kirnberger (1721–1783) learnt from the great JS himself. Despite what you might have been taught, Bach neither invented nor used Equal Temperament. He probably used many different tuning systems—and if he had one particular one in mind for any of his works, he never chose to write clear directions for setting it. Note that his great opus is called the Well-tempered Clavier in English, not the “Equal Tempered Clavichord”, as it has too often been mistranslated. You will find several other Bach temperaments discussed later in this series.There are other commas to learn, and a whole load of other technical guff if you really want to get into this quagmire, but here you will forgive me if we regard the syntonic comma as for all practical purposes the same size as the Pythagorean. After all, don’t you just want to tune your harpsichord instead of go for a science degree?
Here’s how you go about setting Kirnberger III...
Then he explains how to tune a harpischord in this system:
Carey Beebe is my hero these days, because he explains well temperaments better than anyone else I've found. My new style of drawing tuning systems is inspired by his, though I've added some extra twists like drawing all the major thirds, and using colors.
If you're wondering what Beebe and I mean about Pythagorean versus syntonic commas, here you can see it. Here is Kirnberger I drawn in my old style, where I only drew major thirds that are just, and I drew them in dark blue:
Kirnberger I has one fifth that's flat by a factor of the syntonic comma:
But as we go all the way around the circle of fifths the 'total flatness' must equal the Pythagorean comma:
That's just a law of math. So Kirnberger compensated by having one fifth that's flat by a factor of p/σ, which is called the 'schisma':
He stuck this 'schismatic fifth' next to the tritone, since that's a traditional dumping ground for annoying glitches in music. But it barely matters since the schisma is so small.
(That said, the schisma is almost precisely 1/12th of a Pythagorean comma, or more precisely p1/12 — a remarkable coincidence discovered by Kirnberger, which I explained on January 18th. And I did draw the 1/12th commas in equal temperament! So you may wonder why I didn't draw the schisma in Kirnberger I. The answer is simply that in both cases my decision was forced by rules 1 and 2.)
Here's Kirnberger II in a similar style:
Here the schismatic fifth compensates for using two 1/2 commas that are syntonic rather than Pythagorean.
And here's Kirnberger III:
Now the schismatic fifth compensates for using four 1/4 commas that are syntonic rather than Pythagorean.