May 9, 2006

This Week's Finds in Mathematical Physics (Week 231)

John Baez

1) NASA, Enceladus the storyteller, http://www.nasa.gov/mission_pages/cassini/multimedia/pia07800.html

Recently the NASA space probe Cassini has been getting a good look at Enceladus. In March, Cassini discovered that it has geysers among the cracks near its south pole - geysers that spray water right out into space!

2) NASA's Cassini discovers potential liquid water on Enceladus, http://saturn.jpl.nasa.gov/news/press-release-details.cfm?newsID=639

3) Special issue on Enceladus, Science 311 (March 10th 2006).

The water freezes in microscopic crystals, which replenish Saturn's E ring - a diffuse bluish ring that was previously a mystery.

The currently popular theory for the geysers looks like this:

4) NASA, Enceladus "cold geyser" model, http://www.nasa.gov/mission_pages/cassini/multimedia/pia07799.html

Enceladus is now the the only place besides Earth where liquid water has been seen - though people believe Jupiter's moon Europa has oceans under a layer of ice, and maybe Ganymede and Callisto do too.

While we tend to take it for granted, water is a very strange chemical:

5) Martin Chaplin, Forty-one anomalies of water, http://www.lsbu.ac.uk/water/anmlies.html

As you probably know, the specific heat of water is unusually high, which stabilizes the Earth's temperature. And no other simple compound exhibits so many different forms. There at least 18 forms of ice! You can tour them here:

6) Martin Chaplin, The phase diagram of water, http://www.lsbu.ac.uk/water/phase.html

The hexagonal form of ice we find here on earth is called ice Ih. There's also a slightly denser cubic phase, ice Ic, which forms when water vapor is condensed on a cold substrate. Below -130 Celsius, a low-density amorphous solid form called LDA is possible. By compressing ordinary ice Ih to high pressures, you get a different higher-density amorphous form, called HDA. And there's an even denser amorphous form called VHDA.

(It's unusual for a crystal to become amorphous when you compress it or cool it, but ordinary ice is unusually light: it floats on liquid water! That's because the powerful hydrogen bonds of water allow it to maintain a very sparse hexagonal crystal structure - so sparse you could even fit extra water molecules in the gaps. When you crush this, it becomes amorphous.)

There are also crystal forms called ice II through ice XIV, in order of discovery. It would take a few weeks to discuss all these, but luckily Chaplin's website has a separate page on each kind, with nice explanations and pictures of the crystal structures.

Kurt Vonnegut wrote a novel called "Cat's Cradle" starring a substance called ice IX, which was supposedly more stable than liquid water at ordinary temperatures and pressures. When it got loose, it destroyed the world. Luckily the actual ice IX isn't like that, and it couldn't be: the most stable form of water already prevails.

But enough about ice IX. I want to talk about ice X!

This is one of the most extreme forms of ice known. It's only stable at pressures of about 50 gigapascals - in other words, roughly 500,000 atmospheres.

Hmm. Do those quantities mean as little to you as they do to me? A "pascal" is a unit of pressure, or force per area, equal to one newton per square meter. An "atmosphere" is another unit of pressure, basically the average air pressure at sea level here on Earth. This has the annoying value of 101,325 pascals. Personally I have some trouble getting a feel for how much pressure this is, since a newton per square meter isn't much, but 101,325 of them sounds like a lot. So for me, being an American, it's helpful to know that an atmosphere equals 2116 pounds per square foot. If you're a metric sort of person, that's about the weight of 1 kilogram pushing down on each square centimeter. That's a lot of pressure we're under! No wonder we feel stressed sometimes.

(Yes, I know a kilogram is not a unit of weight. I mean the weight corresponding to a mass of a kilogram in the Earth's gravitational field at sea level. Sheesh!)

But I digress. I was saying that ice X only forms at a pressure of about 50 gigapascals. But I've actually read figures ranging from 44 to 80 gigapascals. This raises the question: how do people know these things? Do they actually know, or just guess?

Well, some overgrown kids get paid to study these issues by actually squashing water to enormous pressures using "diamond anvil cells". Not many substances can withstand such huge pressures, but diamonds can: as you know, they're really hard! They're also transparent, so you can see what's going on while you're squashing something. You basically just stick something between two carefully carved diamonds, surrounded by a metal foil gasket, and squash the heck out of it: 7) Diamond anvil cell, Wikipedia, http://en.wikipedia.org/wiki/Diamond_Anvil_Cell

Apparently they can get pressures of up to 360 gigapascals this way, which is the pressure at the center of the Earth.

Another method, which sounds even more fun, is to use a "light gas gun". Here you explode a few kilograms of gunpowder to shoot a piston down a tube. As it shoots forwards, the piston pushes some gas down the tube. The tube narrows to a tiny tip at the end, so the gas is going really fast by the time it shoots out. It shoots out into a much narrower tube, where it pushes a projectile. You can then fire the projectile into something, to generate very high pressures for a very short time.

8) Light gas gun, Wikipedia, http://en.wikipedia.org/wiki/Light_Gas_Gun

It's not called a "light" gas gun because it's wimpy - in fact they're huge, and everyone evacuates the lab when they run the one at NASA! It's called that because the speed of the projectile is limited only by the speed of sound in the gas, which is higher for a light gas like helium - or even better, hydrogen. Even better, that is, you don't mind exploding gunpowder near highly flammable hydrogen! But, as you can imagine, people who do this stuff are precisely the sort who don't mind. You may enjoy reading how folks at Lawrence Livermore National Laboratory used a light gas gun to compress hydrogen to pressures of up to 200 gigapascals, enough to convert it into a metal:

9) Robert C. Cauble, Putting more pressure on hydrogen, http://www.llnl.gov/str/Cauble.html

This supports the theory that the hydrogen at Jupiter's core is in metallic form, which would explain its enormous magnetic field. They know their hydrogen became a metal because they fired a laser at it and saw it was shiny! In fact, they fired three lasers at it simultaneously, just for kicks.

(By the way, this article erroneously says a "megabar" is 100 pascals. It's a million atmospheres, or 100 gigapascals.)

But I'm digressing again. I was saying ice X forms at a pressure of around 50 gigapascals. It's pretty far-out stuff. It's a cubic crystal with density 2.5 times that of ordinary liquid water. It's so compressed that separate water molecules no longer exist! Instead, the oxygen atoms form a body-centered cubic. This means they lie at the corners of a lattice of cubes, but with one at the center of each cube too, like the red dots in this picture by Cavazzoni:

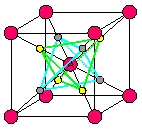
10) Carlo Cavazzoni, Large scale first-principles simulations of water and ammonia at high pressure and temperature, Ph.D. thesis, Scuola Internazionale Superiore di Studi Avanzati, October 1998. Figure 4.10: symmetric and super-ionic ice X structures, p. 57. Available at http://sirio.cineca.it/~acv0/thesis.html

Hydrogen ions - in other words, protons - sit at the midpoints of half the edges connecting cube corners to cube centers. There are two ways they can do this, illustrated by the yellow and gray dots shown above. They can form a right-side-up tetrahedron, or an upside-down tetrahedron.

A body-centered cubic can also be visualized as two interpenetrating cubic lattices, labelled A and B here:

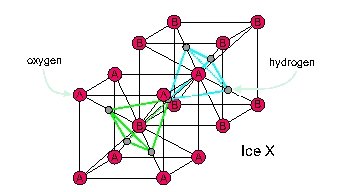
Each oxygen has 4 hydrogens next to it. If you compress water a bit less than enough to make ice X, you get ice VII. This is almost the same, but two of those hydrogens are closer to the oxygen than the other two, so there are still separate water molecules! It's completely random which two hydrogens are closer than the other two. But if you cool down ice VII, you get ice VIII, where it's not random.

So, Nature explores all the options.

Recently people have gotten interested in ice at even higher pressures - and also higher temperatures, to understand the interiors of planets like Neptune and Uranus. Here pressures range from 20 to 800 gigapascals, and temperatures from 2000 to 8000 kelvin. In "week160" I mentioned that on Neptune it may rain diamonds, formed by methane in the atmosphere. But what happens to the water, and the ammonia? If they became good electrical conductors, that might explain the magnetic fields of these planets.

People have done computer simulations to study this:

12) C. Cavazzoni, G. L. Chiarotti, S. Scandolo, E. Tosatti, M. Bernasconi and M. Parrinello, Superionic and metallic states of water and ammonia at giant planet conditions, Science 283 (January 1999), 44-46. Also available at http://www.sciencemag.org/cgi/content/full/283/5398/44

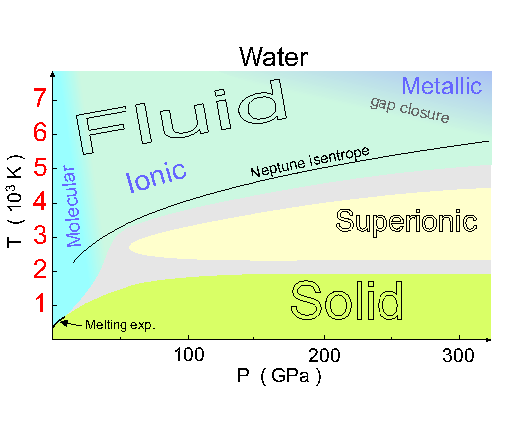
It seems that when you heat up ice X, it goes into a "superionic" state where the little tetrahedra of hydrogen ions in each cube are constantly randomizing themselves, instead of remaining fixed. It's a curious hybrid of a solid and a liquid, since the hydrogens are moving around, while the oxygens stay in their body-centered cubic crystal.

But if you heat it even more, the oxygen melts too! As you can see from the phase diagram above, it then becomes an ionic fluid.

As you heat it even more, you enter the region labelled "gap closure", where the water starts to act like a metallic plasma. Then it's a really good conductor of electricity.

The curve labelled "Neptune isentrope" describes the pressures and temperatures you'd experience if you unwisely jumped into Neptune!

As you fell in, it would keep getting hotter and the pressure would keep rising until you entered this chart, at a temperature of about 2000 kelvin. At this point you'd see molecular fluid water - I say this because at temperatures above 650 kelvin (the critical point for water), there's no sharp difference between liquid and gas. Then the fluid would become ionic... and then you'd start drifting towards gap closure and the metallic plasma phase. Down deep, metallic plasmas of water and ammonia might explain the magnetic field of this planet.

Recently people have done some experiments with water at extremely high pressures, checking what theorists like Cavazzoni and company predict. For example, this paper says that using "extremely large lasers", people have studied water at pressures near a terapascal - 1000 gigapascals:

13) P. M. Celliers et al, Electronic conduction in shock-compressed water, Plasmas 11 (2004), L41-L48.

They also mention that "a single datum at 1.4 terapascals from an underground nuclear experiment has never been repeated." Some people just don't know when to stop in the quest for higher pressures.

While I'm at it, I should mention a few more interesting articles on weird forms of ice. There's a lot of research on this subject! Here's a quick overview:

14) Nancy McGuire, The many phases of water, American Chemical Society, https://web.archive.org/web/20051201104533/http://www.chemistry.org/portal/a/c/s/1/feature_pro.html?id=c373e9fbed0a01c78f6a4fd8fe800100

Here's a webpage with some nice pictures and an interesting story:

15) J. L. Finney, The phase diagram of water and a new metastable form of ice, http://www.cmmp.ucl.ac.uk/people/finney/soi.html

And finally, there's a paper that talks about how ordinary ice Ih but also silica and ice XI become amorphous when you squeeze them enough:

16) Koichiro Umemoto, Renata M. Wentzcovitch, Stefano Baroni and Stefano de Cironcoli, Anomalous pressure-induced transition(s) in ice XI, Physical Review Letters 92 (2004), 105502-1. Also available at http://www.cems.umn.edu/research/wentzcovitch/papers/Phys._Rev._Lett._92_105502_(2004).pdf

There's some interesting math in here, because they do computer simulations of the transition from a crystal to an amorphous substance, which is interesting to study using Fourier analysis. The idea is that certain vibrational modes of the crystal "go soft", so they get easily excited. When a bunch of modes go soft that have wavelengths not equal to the crystal lattice spacing, the crystal structure becomes unstable, and there can be a transition to an amorphous state.

There's also interesting math lurking in Cavazzoni et al's models of ice X! If you think particle physics is hard, just wait until you try understanding something complicated, like water.

I've been sort of obsessed with ice lately. If you like it too, I recommend this book for general information:

16) Mariana Gosnell, Ice: The Nature, the History, and the Uses of an Astonishing Substance, Alfred A. Knopf, New York, 2005.

but I bought this one, because it tells an interesting history of the science of climate change as seen from icy peaks:

17) Mark Bowen, Thin Ice: Unlocking the Secrets of Climate in the World's Highest Mountains, Henry Holt & Co., 2005.

Now for some math. Last week I said a bit about quivers, the McKay correspondence, and string theory. I want to dig deeper into the relation between these subjects, because Urs Schreiber has some interesting ideas about them, which he's mentioned here:

18) Urs Schreiber, A note on RCFT and quiver reps, http://golem.ph.utexas.edu/string/archives/000794.html

But, I'm not feeling sufficiently energetic to explain these ideas right now, especially since he already has! For some more clues, try this:

19) Paul Aspinwall, D-branes on Calabi-Yau manifolds, section 7.3.1, The McKay correspondence, p. 101 and following. Available as hep-th/0403166

For more on the the representation theory of quivers, see the references in the "Addenda" to "week230", and also this excellent book:

20) David J. Benson, Representations and Cohomology I, Cambridge U. Press, Cambridge 1991.

You'll see how the non-simply-laced Dynkin diagrams get into the act! A more thorough treatment, fascinating but somewhat quirky, can be found here:

21) P. Gabriel and A. V. Roiter, Representations of Finite-Dimensional Algebras, Enc. of Math. Sci., 73, Algebra VIII, Springer, Berlin 1992.

If you like category theory you may enjoy this book, because it's all about representations of categories, i.e. functors

F: C → Vect

where C is a category. It's full of nontrivial theorems about these, starting with Gabriel's classification of quivers into those of finite representation type (see "week230"), the tame quivers (which have an infinite but still manageable set of indecomposable representations), and the wild ones. But, you may be puzzled when you read about "svelte" categories, or functors that "preserve heteromorphisms".

I might as well say what those are. A category is "svelte" if its isomorphism classes of objects form a mere set instead of a proper class, like the category of finite-dimensional vector spaces. Most people would say such a category is "essentially small".

And, a functor "preserves heteromorphisms" if it maps heteromorphisms to heteromorphisms. Well, duh! But what's a "heteromorphism"? It's their term for a morphism that's not an isomorphism. Most people would say such a functor "reflects isomorphisms".

You may also be interested in what a "locular" category is, or a "spectroid"... but I won't tell you! Read the book.

Speaking of category theory, this is my last week in Chicago, which is really sad, because Steve Lack is just starting to give us a crash course on "Australian category theory". Australia, you see, is the center of macho category theory, where they're heavy on the calculus of mates, doctrinal adjunctions are a dime a dozen, and everything should be V-enriched if not W-enriched. But Chicago is starting to get macho too: tomorrow Nick Gurski defends his Ph.D. thesis on "Algebraic Tricategories"! So, the Chicago gang wants to learn some tricks from the Australians. But next Monday I'm off to the Perimeter Institute, to indulge the physics side of my personality....

John Baez wrote:

  Now for some math.  Last week I said a bit about quivers, the McKay 
  correspondence, and string theory.   I want to dig deeper into the 
  relation between these subjects,

You want

22) Tom Bridgeland, Alaistair King and Miles Reid, Mukai implies McKay: the McKay correspondence as an equivalence of derived categories, available as math.AG/9908027.

Much coolness there.

  For more on the representation theory of quivers, see the references 
  in the "Addenda" to "week230", and also this excellent book:
  
  20) David J. Benson, Representations and Cohomology I, 
  Cambridge U. Press, Cambridge 1991.  

There's a whole lot of cool things to say about non-Dynkin quivers. If you put a D-brane at an ADE singularity, you get the affine Dynkin quivers, but there are plenty of other singularities out there. Another nice set is the canonical bundle over a del Pezzo with the zero section collapsed. Quivers can be associated to this via a work of Bridgeland:

23) Tom Bridgeland, T-structures on some local Calabi-Yau varieties, available as math.AG/0502050.

with many of the same results in some physics papers by Herzog, Aspinwall and Wijnholt.

My modest contribution to this story is where myself and Nick Proudfoot show that the moduli space of representations of these quivers (for a subclass of examples) has as a component the original cone:

24) Aaron Bergman, Undoing orbifold quivers, available as hep-th/0502105.

Aaron Bergman, Moduli spaces for Bondal quivers, available as math.AG/0512166.

Aaron

© 2006 John Baez
baez@math.removethis.ucr.andthis.edu