September 8, 2006

This Week's Finds in Mathematical Physics (Week 239)

John Baez

David Corfield, Urs Schreiber and I have started up a new blog!

David is a philosopher, Urs is a physicist, and I'm a mathematician, but one thing we all share is a fondness for n-categories. We also like to sit around and talk shop in a public place where our friends can drop by. Hence the title of our blog:

1) The n-Category Café, http://golem.ph.utexas.edu/category

Technologically speaking, the cool thing about this blog is that it uses itex and MathML to let us (and you) write pretty equations in TeX. For this we thank Jacques Distler, who pioneered the technology on his own blog:

2) Jacques Distler, Musings, http://golem.ph.utexas.edu/~distler/blog/

It's great!

Urs began by posting about 11d supergravity and higher gauge theory (see "week237"). Now he's discussing Barrett and Connes' new work on the Standard Model. Meanwhile, I've been obsessed with the categorical semantics of quantum computation, and David has been running discussions on categorifying Klein's Erlangen program (see "week213"), the differences between mathematicians and historians when it comes to writing histories of math, and so on.

And, it's all free.

Meanwhile, in the bad old world of extortionist math publishers, we see a gleam of hope. The entire editorial board of the journal Topology resigned to protest Reed-Elsevier's high prices!

3) Topology board of editors, letter of resignation, http://math.ucr.edu/home/baez/topology-letter.pdf

The board includes some topologists I respect immensely. It takes some guts for full-fledged memmbers of the math establishment to do something like this, and I congratulate them for it. It'll be fun to see what stooges Reed-Elsevier rounds up to form a new board of editors. I can't imagine they'll just declare defeat and let the journal fold.

This is part of trend where journal editors "declare independence" from their publishers and move toward open access:

4) Open Access News, Journal declarations of independence, http://www.earlham.edu/%7Epeters/fos/lists.htm#declarations

Speaking of open access, you can now get the notes from the course Freeman Dyson taught on quantum electrodynamics when he first became a professor of physics at Cornell:

5) Freeman J. Dyson, 1951 Lectures on Advanced Quantum Mechanics, second edition, available as quant-ph/0608140. For historical context and original mimeographs, see http://hrst.mit.edu/hrs/renormalization/dyson51-intro/

These notes are from an exciting period in physics, shortly after the 1947 Shelter Island conference where Feynman and Schwinger presented their approaches to quantum electrodynamics to an audience of luminaries including Bohr, Oppenheimer, von Neumann, and Weisskopf. Nobody understood Feynman's diagrams except Schwinger and maybe Feynman's thesis advisor, John Wheeler.

Every true fan of physics loves reading about this heroic era and its figures, especially Feynman. So, if you haven't read these yet, run to the bookstore and buy them now!

6) James Gleick, Genius: the Life and Science of Richard Feynman, Vintage Press, 1993.

7) Jagdish Mehra, The Beat of a Different Drum: the Life and Science of Richard Feynman, Oxford U. Press, 1996.

8) Silvan S. Schweber, QED and the Men Who Made It, Princeton U. Press, Princeton, 1994.

The first book is a barrel of fun but doesn't get into the nitty-gritty details of Feynman's work. The second more scholarly treatment also has lots of Feynman anecdotes - even some new ones! But, it covers his work in enough detail to intimidate any non-physicist. The third offers a broader panorama of the development of quantum electrodynamics. Taken together, they add up to quite a nice story.

Of course, I'm assuming you've read these:

9) Richard P. Feynman, Surely You're Joking, Mr. Feynman! (Adventures of a Curious Character), W. W. Norton and Company, New York, 1997.

10) Richard P. Feynman, What Do You Care What Other People Think? (Further Adventures of a Curious Character), W. W. Norton and Company, New York, 2001.

They're more fun than everything else I've ever recommended on This Week's Finds, combined. If you haven't read them, don't just run to the nearest bookstore - get in a time machine, go back, and make sure you did read them.

Today I'd like to wrap up the discussion of Koszul duality which I began last Week. As we'll see, this gives a really efficient way of categorifying the theory of Lie algebras and defining "Lie n-algebras". And, as Urs Schreiber notes, these seem to be just what we need to understand 11-dimensional supergravity in a nice geometric way.

But before I dive into this heavy stuff, something fun. Thanks to Christine Dantas' blog, I just saw a webpage on the origins of math and writing in Mesopotamia:

11) Duncan J. Melville, Tokens: the origin of mathematics, from his website Mesopotamian Mathematics, http://it.stlawu.edu/%7Edmelvill/mesomath/

Before people in the Near East wrote on clay tablets, there were "tokens":

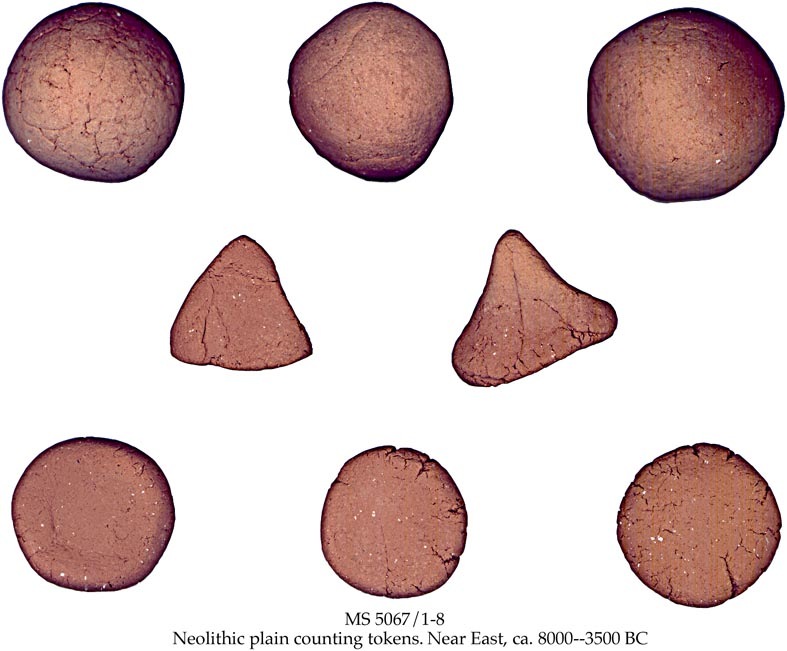
12) The Schøyen Collection, MS 5067/1-8, Neolithic plain counting tokens possibly representing 1 measure of grain, 1 animal and 1 man or 1 day's labour, respectively, http://www.nb.no/baser/schoyen/5/5.11/index.html

These are little geometric clay figures that represented things like sheep, jars of oil, and various amounts of grain. They are found throughout the Near East starting with the agricultural revolution in about 8000 BC. Apparently they were used for contracts!

Eventually groups of tokens were sealed in clay envelopes, so any attempt to tamper with them would be visible.

But, it's annoying to have to break a clay envelope just to see what's in it. So, after a while, they started marking the envelopes to say what was inside. At first, they did this simply by pressing the tokens into the soft clay of the envelopes.

Later, these marks were simply drawn on tablets. Eventually they gave up on the tokens - a triumph of convenience over security. The marks on tablets then developed into the Babylonian number system! The transformation was complete by 3000 BC.

So, five millennia of gradual abstraction led to the writing of numbers! From three tokens representing jars of oil, we eventually reach the abstract number "3" applicable to anything.

Of course, all history is detective work. The story I just told is an interpretation of archaeological evidence. It could be wrong. This particular interpretation is due to Denise Schmandt-Besserat. It seems to be fairly well accepted in broad outline, but scholars are still arguing about it.

For more on her ideas, try this:

13) Denise Schmandt-Besserat, Accounting with tokens in the ancient Near East, http://www.utexas.edu/cola/centers/lrc/numerals/dsb/dsb.html

For a bibliography of her many papers, try:

14) Denise Schmandt-Besserat, Publications, http://www.utexas.edu/cola/centers/lrc/iedocctr/ie-pubs/dsb-pubs.html

For more work on this subject - I want to read more! - try:

15) Eleanor Robson, Bibliography of Mesopotamian mathematics, http://it.stlawu.edu/~dmelvill/mesomath/erbiblio.html

And for a fun intro to writing on clay tablets, try this:

16) John Heise, Cuneiform writing system, http://xoomer.alice.it/bxpoma/akkadeng/cuneiform.htm

Next, from 8000 BC, let's shoot forward ten millennia straight into the 20th century. Last week I gave three examples of Koszul duality:

Making the free graded-commutative algebra on SL* into a differential graded-commutative algebra is the same as making L into a Lie algebra.

Making the free graded Lie algebra on SL* into a differential graded Lie algebra is the same as making L into a commutative algebra.

Making the free graded associative algebra on SL* into a differential graded associative algebra is the same as making L into an associative algebra.

Now, what if we replace L by a graded vector space that can have stuff of any degree? We get a fancier version of Koszul duality, which goes like this:

Making the free graded-commutative algebra on SL* into a differential graded-commutative algebra is the same as making L into an L_∞-algebra.

Making the free graded Lie algebra on SL* into a differential graded Lie algebra is the same as making L into a C_∞-algebra.

Making the free graded associative algebra on SL* into a differential graded associative algebra is the same as making L into an A_∞-algebra.

Similarly, a "C_∞-algebra" is a chain complex that's like a graded-commutative algebra up to homotopy, ad infinitum.

Similarly, an "A_∞-algebra" is a chain complex that's like an associative algebra up to homotopy, ad infinitum. Here you can read off all the higher homotopies from the Stasheff associahedra, which you know and love from "week144" - but again, Koszul duality means you don't have to!

As mentioned last week, all this stuff generalizes to any kind of algebraic gadget in Vect - the category of vector spaces - which is defined by a "quadratic operad" O. Any such operad has a "Koszul dual" operad O* such that:

Making the free graded O*-algebra on SL* into a differential graded O*-algebra is the same as making L into an O_∞-algebra.

Here O_∞ is an operad in the category of chain complexes defined by "weakening" O in a systematic way - replacing all the laws by chain homotopies, ad infinitum. We can define O_∞ using the "bar construction", as nicely described here:

16) Todd Trimble, Bar constructions, http://math.ucr.edu/home/baez/trimble/bar.html

or in the book by Markl, Schnider and Stasheff:

17) Martin Markl, Steve Schnider and Jim Stasheff, Operads in Algebra, Topology and Physics, AMS, Providence, Rhode Island, 2002.

See "week191" for more on this book, and what the heck an "operad" is. By the way, we have

O** ≅ O

so we can also say:

Making the free graded O-algebra on SL* into a differential graded O-algebra is the same as making L into an O*_∞-algebra.

Anyway, I don't have much intuition for how Koszul duality lets us magically sidestep the bar construction of O_∞. Someday I hope I'll understand this.

But, once we have the concept of "L_∞-algebra", we can restrict ourselves to chain complexes that vanish except for their first n terms - that is, degrees 0, 1, ..., n-1 - and get the concept of "Lie n-algebra".

In fact, a Lie n-algebra is like a hybrid of a Lie algebra and an n-category! The definition I just gave says a Lie n-algebra is an L_∞-algebra which as a chain complex vanishes above degree n-1. But, such chain complexes are equivalent to strict n-category objects in Vect! So, we can think of Lie n-algebras as strict n-categories that do their best to act like Lie algebras, but with some of the laws holding up to isomorphism, with these isomorphisms satisfying their own laws up to isomorphism, etcetera.

But, the really cool part is that we can do gauge theory using Lie n-algebras instead of Lie algebras, and taking n = 3 we get an example that seems to explain the geometry of 11d supergravity... that is, the classical limit of that mysterious thing called M-theory.

For this, you really need to read Urs Schreiber's stuff:

18) Urs Schreiber, Castellani on free differential algebras in supergravity: gauge 3-group of M-theory, http://golem.ph.utexas.edu/string/archives/000840.html

19) Urs Schreiber, SuGra 3-connection reloaded, http://golem.ph.utexas.edu/category/2006/08/sugra_3connection_reloaded.html

and many other things he's been writing on the n-Category Café lately.

Addenda: You can see discussion of this Week's Finds at the n-Category Café. In his blog Not Even Wrong, Peter Woit has more to say about the open access movement and a questionable plan broached by CERN to pay for-profit journals to make their papers freely available. Some comments on this blog article dig deeper into the evolution of Babylonian numerals:

19) John Baez and Richard Elwes, Babylon and the square root of 2, Azimuth, December 2nd, 2011, http://johncarlosbaez.wordpress.com/2011/12/02/babylon-and-the-square-root-of-2/.

© 2006 John Baez
baez@math.removethis.ucr.andthis.edu