




|
 
|

|
Symmetry has fascinated us throughout the ages. Greek settlers in Sicily may have seen irregular 12-sided crystals of pyrite in Sicily and dreamt up the regular dodecahedron simply because it was more beautiful, more symmetrical.
The Alhambra, a Moorish palace in Granada built around 1300, has tile patterns with at least 13 of the 17 possible symmetry groups:
1) Branko Grünbaum, What symmetry groups are present in the Alhambra?, Notices of the AMS, 53 (2006), 670-673. Also available at http://www.ams.org/notices/200606/comm-grunbaum.pdf
You can see some of these patterns here:
2) Moresque tiles, http://www.spsu.edu/math/tile/grammar/moor.htm
Recently, Peter Lu and Paul Steinhardt discovered that Islamic tile designs also include "quasicrystals". A perfectly repetitive tiling can't have 5-fold symmetry. Nor can a 3-dimensional crystal: that's why the dodecahedra formed by pyrite aren't regular. But by using patterns that never quite repeat, the Islamic artists achieved approximate 5-fold symmetry:
3) Peter J. Lu and Paul J. Steinhardt, Decagonal and quasi-crystalline tilings in medieval Islamic architecture, Science 315 (2007), 1106-1110.
Here's an example from the I'timad al-Daula mausoleum in the Indian city of Agra, built by Islamic conquerors in 1622 - together with a more mathematical version constructed by Lu and Steinhardt:
Here's another, from the Darb-i Imam shrine in Isfahan, Iran, also built in the 1600s:
This came as a big surprise, since everyone had thought that the math behind quasicrystals was first discovered by Penrose around 1974, then seen in nature by Shechtman, Blech, Gratias and Cahn in 1983. It goes to show that the appeal of symmetry, even in its subtler forms, is very old! It also goes to show that you can make big discoveries just by looking carefully at what's in front of you.
For more on quasicrystals, try this:
4) Steven Webber, Quasicrystals, http://www.jcrystal.com/steffenweber/
Of course, the appeal of symmetry didn't end with ancient Greeks or medieval Islamic monarchs. It also seems to have gotten ahold of John Fry, chief executive of Fry's Electronics - a chain of retail shops whose motto is "Your best buys are always at Fry's". In 1994 he set up something called the American Institute of Mathematics. The headquarters was in a Fry's store in Palo Alto - not very romantic. But last year, this institute announced plans to move to a full-scale replica of the Alhambra!
5) Associated Press, Silicon valley will get Alhambra-like castle, August 18, 2006. Available at http://www.jcrystal.com/steffenweber/
And this week, the institute flexed its mighty PR muscles and coaxed reporters from the New York Times, BBC, Le Monde, Scientific American, Science News, and so on to write about a highly esoteric advance in our understanding of symmetry - a gargantuan calculation involving the Lie group E8:
6) American Institute of Mathematics, Mathematicians map E8, http://aimath.org/E8
The calculation is indeed huge. The answer takes up 60 gigabytes of data: the equivalent of 45 days of music in MP3 format. If this information were written out on paper, it would cover Manhattan!
But what's the calculation about? It almost seems a good explanation of that would also cover Manhattan. I took a stab at it here:
7) John Baez, News about E8, http://golem.ph.utexas.edu/category/2007/03/news_about_e8.html
but I only got as far as sketching a description of E8 and some gadgets called R-polynomials. Then come Kazhdan-Lusztig polynomials, and Kazhdan-Lusztig-Vogan polynomials.... For more details, follow the links, especially to the page written by Jeffrey Adams, who led the project.
In weeks to come, I'll say more about some topics tangentially related to this calculation - especially flag varieties, representation theory and the Weil conjectures. I may even talk about Kazhdan-Lusztig polynomials!
For starters, though, let's just look at some pretty pictures by John Stembridge that hint at the majesty of E8. Then I'll sketch the real subject of Weeks to come: symmetry, geometry, and "groupoidification".
To warm up to E8, let's first take a look at D4, D5, E6, and E7.
In "week91" I spoke about the D4 lattice. To get this, first take a bunch of equal-sized spheres in 4 dimensions. Stack them in a hypercubical pattern, so their centers lie at the points with integer coordinates. A bit surprisingly, there's a lot of room left over - enough to fit in another copy of this whole pattern: a bunch of spheres whose centers lie at the points with half-integer coordinates!
If you stick in these extra spheres, you get the densest known packing of spheres in 4 dimensions. Their centers form the "D4 lattice". It's an easy exercise to check that each sphere touches 24 others. The centers of these 24 are the vertices of a marvelous shape called the "24-cell" - one of the six 4-dimensional Platonic solids. It looks like this:
8) John Baez, picture of 24-cell, in a review of On Quaternions and Octonions: Their Geometry, Arithmetic and Symmetry, by John H. Conway and Derek A. Smith, available at http://math.ucr.edu/home/baez/octonions/conway_smith/
Here I'm using a severe form of perspective to project 4 dimensions down to 2. The coordinate axes are drawn as dashed lines; the solid lines are the edges of the 24-cell.
How about in 5 dimensions? Here the densest known packing of spheres uses the "D5 lattice". This is a lot like the D4 lattice... but only if you think about it the right way.
Imagine a 4-dimensional checkerboard with "squares" - really hypercubes! - alternately colored red and black. Put a dot in the middle of each black square. Voila! You get a rescaled version of the D4 lattice. It's not instantly obvious that this matches my previous description, but it's true.
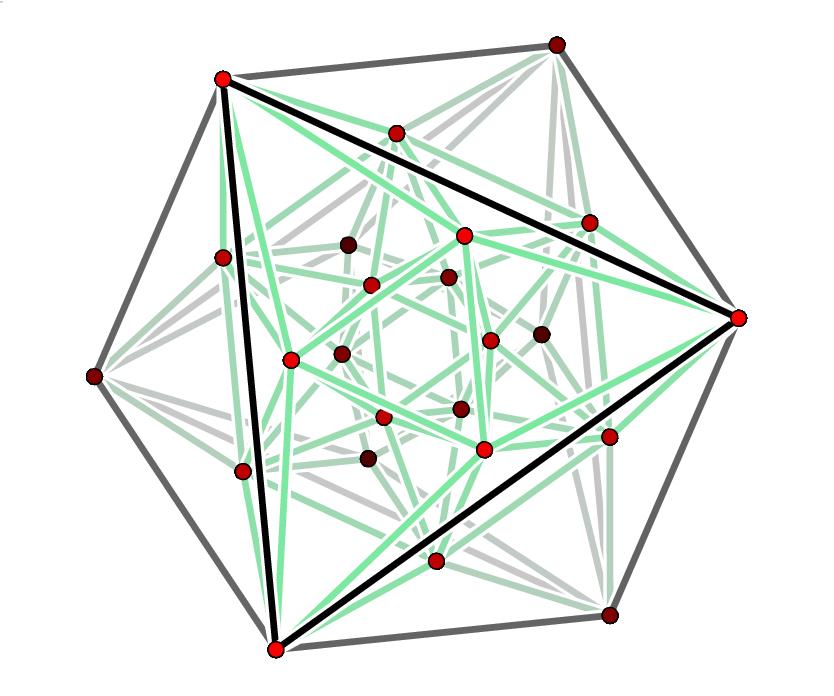
If you do the same thing with a 5-dimensional checkerboard, you get the "D5 lattice", by definition. This gives the densest known packing of spheres in 5 dimensions. In this packing, each sphere has 40 nearest neighbors. The centers of these nearest neighbors are the vertices of a solid that looks like this:
9) John Stembridge, D5 root system, available at http://www.math.lsa.umich.edu/~jrs/data/coxplanes/
If you do the same thing with a 6-dimensional checkerboard, you get the "D6 lattice"... and so on.
However, in 8 dimensions something cool happens. If you pack spheres in the pattern of the D8 lattice, there's enough room left to stick in an extra copy of this whole pattern! The result is called the "E8 lattice". It's twice as dense as the D8 lattice.
If you then take a well-chosen 7-dimensional slice through the origin of the E8 lattice, you get the E7 lattice. And if you take a well-chosen 6-dimensional slice of this, you get the E6 lattice. For precise details on what I mean by "well-chosen", see "week65".
E6 and E7 give denser packings of spheres than D6 and D7. In fact, they give the densest known packings of spheres in 6 and 7 dimensions!
In the E6 lattice, each sphere has 72 nearest neighbors. They form the vertices of a solid that looks like this:
10) John Stembridge, E6 root system, available at http://www.math.lsa.umich.edu/~jrs/data/coxplanes/
In the E7 lattice, each sphere has 126 nearest neighbors. They form the vertices of a solid like this:
11) John Stembridge, E7 root system, available at http://www.math.lsa.umich.edu/~jrs/data/coxplanes/
In the E8 lattice, each sphere has 240 nearest neighbors. They form the vertices of a solid like this:
12) John Stembridge, E8 root system, available at http://www.math.lsa.umich.edu/~jrs/data/coxplanes/
Faithful readers will know I've discussed these lattices often before. For how they give rise to Lie groups, see "week63". For more about "ADE classifications", see "week64" and "week230". I haven't really added much this time, except Stembridge's nice pictures. I'm really just trying to get you in the mood for a big adventure involving all these ideas: the Tale of Groupoidification!
If we let this story lead us where it wants to go, we'll meet all sorts of famous and fascinating creatures, such as:
However, the charm of the tale is how many of these ideas are unified and made simpler thanks to a big, simple idea: groupoidification.
So, what's groupoidification? It's a method of exposing the combinatorial underpinnings of linear algebra - the hard bones of set theory underlying the flexibility of the continuum.
Linear algebra is all about vector spaces and linear maps. One of the lessons that gets drummed into you when you study this subject is that it's good to avoid picking bases for your vector spaces until you need them. It's good to keep the freedom to do coordinate transformations... and not just keep it in reserve, but keep it manifest!
As Hermann Weyl wrote, "The introduction of a coordinate system to geometry is an act of violence".
This is a deep truth, which hits many physicists when they study special and general relativity. However, as Niels Bohr quipped, a deep truth is one whose opposite is also a deep truth. There are some situations where a vector space comes equipped with a god-given basis. Then it's foolish not to pay attention to this fact!
The most obvious example is when our vector space has been defined to consist of formal linear combinations of the elements of some set. Then this set is our basis.
This often happens when we use linear algebra to study combinatorics.
But if sets give vector spaces, what gives linear operators? Your first guess might be functions. And indeed, functions between sets do give linear operators between their vector spaces. For example, suppose we have a function
f: {livecat, deadcat} → {livecat, deadcat}
which "makes sure the cat is dead":
f(livecat) = deadcat
f(deadcat) = deadcat
Then, we can extend f to a linear operator defined on formal linear combinations of cats:
F(a livecat + b deadcat) = a deadcat + b deadcat
Written as a matrix in the {livecat, deadcat} basis, this looks like
0 0 1 1(The relation to quantum mechanics here is just a vague hint of themes to come. I've deliberately picked an example where the linear operator is not unitary.)
So, we get some linear operators from functions... but not all! We only get operators whose matrices have exactly a single 1 in each column, the rest of the entries being 0. That's because a function f: X → Y sends each element of X to a single element of Y.
This is very limiting. We can do better if we get operators from relations between sets. In a relation between sets X and Y, an element of X can be related to any number of elements of Y, and vice versa. For example, let the relation
R: {1,2,3,4} —/→ {1,2,3,4}
be "is a divisor of". Then 1 is a divisor of everybody, 2 is a divisor of itself and 4, 3 is only a divisor of itself, and 4 is only a divisor of itself. We can encode this in a matrix:
1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 1where 1 means "is a divisor of" and 0 means "is not a divisor of".
We can get any matrix of 0's and 1's this way. Relations are really just matrices of truth values. We're thinking of them as matrices of numbers. Unfortunately we're still far from getting all matrices of numbers!
We can do better if we get matrices from spans of sets. A span of sets, written S: X —/→ Y, is just a set S equipped with functions to X and Y. We can draw it like this:
S
/ \
/ \
F/ \G
/ \
v v
X Y
This is my wretched ASCII attempt to draw two arrows coming down from
the set S to the sets X and Y. It's supposed to look like a bridge -
hence the term "span".
Spans of sets are like relations, but where you can be related to someone more than once!
For example, X could be the set of Frenchman and Y could be the set of Englishwomen. S could be the set of Russians. As you know, every Russian has exactly one favorite Frenchman and one favorite Englishwoman. So, F could be the function "your favorite Frenchman", and G could be "your favorite Englishwoman".
Then, given a Frenchman x and an Englishwoman y, they're related by the Russian s whenever s has x as their favorite Frenchman and y as their favorite Englishwoman:
F(s) = x and G(s) = y.
Some pairs (x,y) will be related by no Russians, others will be related by one, and others will be related by more than one! I bet the pair
(x,y) = (Gérard Depardieu, Emma Thompson)
is related by at least 57 Russians.
This idea lets us turn spans of sets into matrices of natural numbers. Given a span of finite sets:
S
/ \
/ \
F/ \G
/ \
v v
X Y
we get an X × Y matrix whose (x,y) entry is the number of Russians -
I mean elements s of S - such that
F(s) = x and G(s) = y.
We can get any finite-sized matrix of natural numbers this way.
Even better, there's a way to "compose" spans that nicely matches the usual way of multiplying matrices. You can figure this out yourself if you solve this puzzle:
Let X be the set of people on Earth. Let T be the X × X matrix corresponding to the relation "is the father of". Why does the matrix T2 correspond to the relation "is the paternal grandfather of"? Let S correspond to the relation "is a friend of". Why doesn't the matrix S2 correspond to the relation "is a friend of a friend of"? What span does this matrix correspond to?
To go further, we need to consider spans, not of sets, but of groupoids!
I'll say more about this later - I suspect you're getting tired. But for now, briefly: a groupoid is a category with inverses. Any group gives an example, but groupoids are more general - they're the modern way of thinking about symmetry.
There's a way to define the cardinality of a finite groupoid:
12) John Baez and James Dolan, From finite sets to Feynman diagrams, in Mathematics Unlimited - 2001 and Beyond, vol. 1, eds. Bjorn Engquist and Wilfried Schmid, Springer, Berlin, 2001, pp. 29-50. Also available as math.QA/0004133.
And, this can equal any nonnegative rational number! This lets us generalize what we've done from finite sets to finite groupoids, and get rational numbers into the game.
A span of groupoids is a diagram
S
/ \
/ \
F/ \G
/ \
v v
X Y
where X, Y, S are groupoids and F, G are functors. If all the groupoids
are finite, we can turn this span into a finite-sized matrix of nonnegative
rational numbers, by copying what we did for spans of finite sets.
There's also a way of composing spans of groupoids, which corresponds to multiplying matrices. However, there's a trick involved in getting this to work - I'll have to explain this later. For details, try:
13) Jeffrey Morton, Categorified algebra and quantum mechanics, Theory and Application of Categories 16 (2006), 785-854. Available at http://www.emis.de/journals/TAC/volumes/16/29/16-29abs.html; also available as math.QA/0601458.
14) Simon Byrne, On Groupoids and Stuff, honors thesis, Macquarie University, 2005, available at http://www.maths.mq.edu.au/~street/ByrneHons.pdf and http://math.ucr.edu/home/baez/qg-spring2004/ByrneHons.pdf
Anyway: the idea of "groupoidification" is that in many cases where mathematicians think they're playing around with linear operators between vector spaces, they're actually playing around with spans of groupoids!
This is especially true in math related to simple Lie groups, their Lie algebras, quantum groups and the like. While people usually study these gadgets using linear algebra, there's a lot of combinatorics involved - and where combinatorics and symmetry show up, one invariably finds groupoids.
As the name suggests, groupoidification is akin to categorification. But, it's a bit different. In categorification, we try to boost up mathematical ideas this way:
sets → categories
functions → functors
In groupoidification, we try this:
vector spaces → groupoids
linear operators → spans of groupoids
Actually, it's "decategorification" and "degroupoidification" that are systematic processes. These processes lose information, so there's no systematic way to reverse them. But, as I explained in "week99", it's still fun to try! If we succeed, we discover an extra layer of structure beneath the math we thought we understood... and this usually makes that math clearer and less technical, because we're not seeing it through a blurry, information-losing lens.
Okay, that's enough for now. On a completely different note, here's a book on "structural realism" and quantum mechanics:
15) Dean Rickles, Steven French, and Juha Saatsi, The Structural Foundations of Quantum Gravity, Oxford University Press, Oxford, 2006. Containing:
Dean Rickles and Steven French, Quantum gravity meets structuralism: interweaving relations in the foundations of physics. Also available at http://fds.oup.com/www.oup.co.uk/pdf/0-19-926969-6.pdfTian Yu Cao, Structural realism and quantum gravity.
John Stachel, Structure, individuality, and quantum gravity. Also available as gr-qc/0507078.
Oliver Pooley, Points, particles, and structural realism. Also available at http://philsci-archive.pitt.edu/archive/00002939/
Mauro Dorato and Massimo Pauri, Holism and structuralism in classical and quantum general relativity. Also available at http://philsci-archive.pitt.edu/archive/00001606/
Dean Rickles, Time and structure in canonical gravity. Also available at http://philsci-archive.pitt.edu/archive/00001845/
Lee Smolin, The case for background independence. Also available as hep-th/0507235.
John Baez, Quantum quandaries: A category-theoretic perspective. Also available at http://math.ucr.edu/home/baez/quantum/ and as quant-ph/0404040.
Very loosely speaking - I ain't no philosopher - structural realism is the idea that what's "real" about mathematics, or the abstractions in physical theories, are not individual entities but the structures, or patterns, they form. So, instead of asking tired questions like "What is the number 2, really?" or "Do points of spacetime really exist?", we should ask more global questions about the roles that structures like "natural numbers" or "spacetime" play in math and physics. It's a bit like how in category theory, we can only understand an object in the context of the category it inhabits.
Finally, here's a puzzle for lattice and Lie group fans. The dots in Stembridge's pictures are the shortest nonzero vectors in the D5, E6, E7, and E8 lattices - or in technical terms, the "roots". Of course, only for ADE Dynkin diagrams are the roots all of equal length - but those are the kind we have here. Anyway: in the D5 case, only 32 of the 40 roots are visible. The other 8 are hidden in back somewhere. Where are they?
I asked John Stembridge about this and he gave a useful clue. His planar pictures show projections of the roots into what he calls the "Coxeter plane".
Recall from "week62" that the "Coxeter group" associated to a Dynkin diagram acts as rotation/reflection symmetries of the roots; it's generated by reflections through the roots. There's a basis of roots called "simple roots", one for each dot in our Dynkin diagram, and the product of reflections through all these simple roots is called the "Coxeter element" of our Coxeter group - it's well-defined up to conjugation. The "Coxeter plane" is the canonical plane on which the Coxeter element acts as a rotation.
A rotation by how much? The order of the Coxeter element is called the "Coxeter number" and denoted h, so the Coxeter element acts on the Coxeter plane as a rotation of 2π/h. The Coxeter number is important for other reasons, too! Here's how it goes:
Coxeter group Coxeter number An n+1 Bn 2n Cn 2n Dn 2n-2 E6 12 E7 18 E8 30 F4 12 G2 6
For D5 the Coxeter number is 8, which accounts for the 8-fold symmetry of Stembridge's picture in that case. The E8 picture has 30-fold symmetry! My D4 picture has 8-fold symmetry, so I must not have been projecting down to the Coxeter plane.
Anyway, this stuff should help answer my puzzle. I don't know the answer, though.
Addenda: I thank David Corfield and James Dolan for catching mistakes. Tony Smith found a nice picture created by Günter Ziegler of the D4 root system (that is, the 24-cell) viewed from the Coxeter plane. The D4 root system is 4-dimensional, but it's been drawn with a bit of 3d perspective. The 6-fold symmetry is evident:
16) Günter M. Ziegler, picture of 24-cell, http://www.math.tu-berlin.de/~ziegler/24-cell.jpeg
For more discussion, go to the n-Category Café.
© 2007 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|