




|
 
|

|
This week I'll talk about quasicrystals and how they arise from the interplay between crystallographic and noncrystallographic Coxeter groups. I'll describe Jeffrey Morton's new paper on groupoids and 2-vector spaces, and Stephen Summers' review of new work on constructive quantum field theory. But first - more pictures of Jupiter's moon Io!
Here's a great photo of volcanic activity on Io - the "Masubi plume":

1) NASA Photojournal, Masubi plume on Io, http://photojournal.jpl.nasa.gov/catalog/PIA02502
You can see hot gas and dust shooting 100 kilometers up into the atmosphere!
Here's another:

2) Solarviews, Pele volcano and Pillan Patera, http://www.solarviews.com/eng/iopele.htm
In front we see a volcanic feature called Pillan Patera. Over the horizon we see an enormous eruption 300 kilometers high coming from the most intense persistent hot spot on Io: Pele. This seems to be an active lava lake inside a volcanic depression, or "patera", about 20 x 30 kilometers in size.
But Pillan Patera is no slouch either when it comes to eruptions. Look at these "before and after" pictures taken 5 months apart in 1997:
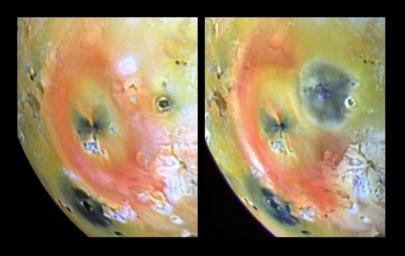
3) NASA Photojournal, Arizona-sized Io eruption, http://photojournal.jpl.nasa.gov/catalog/PIA00744
The big red ring is sulfur spewed out by Pele. But the exciting new feature in the "after" picture is the dark blotch centered at Pillan Patera. It's 400 kilometers in diameter, roughly the size of Arizona. It consists of about 50 cubic kilometers of lava laid down by a big eruption. At the peak of the activity, 10,000 cubic meters of lava were spewing out each second. This was the largest volcanic eruption ever seen, anywhere!
For more, try these:
4) A.G. Davies et al, Thermal signature, eruption style and eruption evolution at Pele and Pillan on Io, Jour. Geophys. Research 106 (2001), 33,079-33,103. Also available at http://europa.la.asu.edu/pgg/associates/members/williams/gw/pdf/2001Daviesetal.pdf
5) Jani Radebaugh et al, Observations and temperatures of Io's Pele Patera from Cassini and Galileo spacecraft images, Icarus 169 (2004), 65-79.
In case you're wondering about the red sulfur around Pele versus the yellow sulfur you saw last week, let me say a bit about that. Sulfur comes in an incredible number of forms, or allotropes:
6) Wikipedia, Allotropes of sulfur, http://en.wikipedia.org/wiki/Allotropes_of_sulfur
It can form different molecules consisting of 2 to 20 atoms. The most common form on Earth is α-sulfur: rhombic crystals made of ring-shaped molecules containing 8 atoms each:
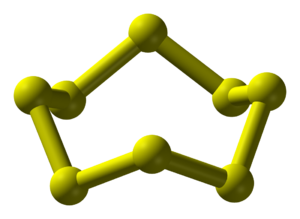
α-sulfur is lemon yellow, but above 95 degrees Celsius it gradually turns into pale yellow β-sulfur: the ring-shaped molecules reorganize to form crystals with less symmetry - monoclinic crystals, to be precise.
Sulfur melts around 115 Celsius. But when you heat it above 160
Celsius, something weird happens: contrary to the usual pattern for
liquids, it gets more viscous as it gets hotter! The reason: the
atoms start forming long chain polymers, called "catena
sulfur". As these predominate, the stuff gets darker in color:
first orange, then red, then dark red, and finally almost black.
Blecch! If you then cool it suddenly, it can form a red amorphous
solid. And that, presumably, is what we see in the ring around Pele.
Now, from crystals to quasicrystals...
Last week I asked if quasicrystals with approximate 5-fold symmetry
could be obtained by slicing lattices in higher dimensions. Greg
Egan answered - yes! He even has a beautiful Java applet that
demonstrates it:
7) Greg Egan, deBruijn,
http://www.gregegan.net/APPLETS/12/12.html
It shows some nice quasiperiodic tilings of the plane with approximate
n-fold symmetry, made by cleverly slicing a cubical lattice in
n-dimensional space. Here's a piece of one for n = 4:
The idea comes from this paper:
8) N. G. deBruijn, Algebraic theory of Penrose's nonperiodic tilings
of the plane, I, II, Nederl. Akad. Wetensch. Indag. Math. 43 (1981),
39-52, 53-66.
When n is odd, we can also get deBruijn's tiling by slicing the
An-1 lattice in (n-1)-dimensional space. You're probably
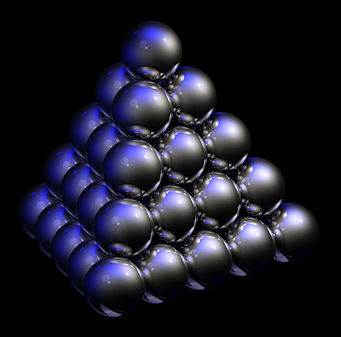
most familiar with the A3 lattice, which shows up when you
stack oranges:
You'll notice this pattern has tetrahedral symmetry. The symmetry
group of the tetrahedron is also called the A3 Coxeter
group. It's the group of all permutations of 4 things (the corners of
the tetrahedron). This contains the symmetry group of the square,
since that group contains some but not all permutations of the 4
corners of the square. Indeed, if you view a regular tetrahedron from
the correct angle, it looks like a square!
This pattern goes on for higher n. Last week I spoke about the
A4 lattice, whose symmetry group consists of all
permutations of 5 things - namely the 5 corners of a 4-simplex, which
is the 4d analogue of a tetrahedron. I explained how this group
contains the symmetry group of the pentagon. Indeed, if you view a
4-simplex from the correct angle, it looks like a pentagon!
So, it's not surprising that we can get a quasiperiodic tiling of the plane
with approximate 5-fold symmetry by taking a 2d slice of the
A4 lattice and doing a few other tricks. Here's a piece:
But this generalizes:
the symmetries of an (n-1)-simplex include the symmetries of a regular
n-gon. In other words, just as this Coxeter group, the symmetry
group of the pentagon:
You can see details on Greg Egan's page above.
Here's a piece of the tiling for n = 7, again courtesy of Egan's
applet:
And this idea generalizes to the other two
noncrystallographic Coxeter groups. Remember, there are just two
more:
We can get 3d quasicrystals with approximate dodecahedral symmetry by
cleverly slicing the 6-dimensional D6 lattice. This is
actually practical, since there really are such quasicrystals
in nature. And we can get 4d quasicrystals with approximate 120-cell
symmetry by cleverly slicing the E8 lattice! This is just
incredibly cool as pure mathematics:
9) Veit Elser and Neil Sloane, A highly symmetric four-dimensional
quasicrystal, J. Phys. A 20 (1987), 6161-6168.
Also available at http://akpublic.research.att.com/~njas/doc/Elser.ps
10) J. F. Sadoc and R. Mosseri, The E8 lattice and
quasicrystals: geometry, number theory and quasicrystals, J. Phys. A
26 (1993), 1789-1809.
11) Robert V. Moody and J. Patera, Quasicrystals and icosians,
J. Phys. A. 26 (1993), 2829-2853.
Yes, this is the same Moody who helped invent Kac-Moody algebras! For
the last decade or so he's been working on quasicrystals. In "week20" I explained the
"icosians" - a subring of the quaternions built from the
symmetries of a dodecahedron - and how Conway and Sloane used them to
construct the E8 lattice. Moody's article uses the
icosians to study the 4d quasicrystals that we get by slicing the
E8 lattice.
While they may seem remote from the real world, these 4d quasicrystals
can be further sliced to give 3d quasicrytals with approximate
dodecahedral symmetry. So in some sense, the quasicrystals we find
in nature are "shadows" of the E8
lattice... trying their best to have a symmetry that can only exist in
8 dimensions, but never quite succeeding.
I love this idea, because it's gotten me over my fear of
quasicrystals. They look unruly and complicated, but now I see that
some of them have close ties to the beautiful, perfectly symmetrical
world of Dynkin diagrams. The "noncrystallographic" Coxeter
groups are really "quasicrystallographic"!
Next let me discuss this paper by Jeffrey Morton:
11) Jeffrey Morton, 2-vector spaces and groupoids, available as
arXiv:0810.2361.
It's an important new twist in the Tale of Groupoidification! As
part of this tale, in "week256"
I described a functor from the category with
Jeffrey boosts this idea up one notch, getting a 2-functor from
the 2-category with
Here by "finite-dimensional 2-vector space" I really mean a
"Kapranov-Voevodsky 2-vector space". That's a category
equivalent to Vectn for some n, where Vect is the category
of finite-dimensional vector spaces. A "linear functor" is
one that's linear on each homset. More concretely, we can describe a
linear functor
F: Vectn → Vectm
as an m × n matrix of finite-dimensional vector spaces, just as
we can describe a linear operator
F: Cn → Cm
as a m × n matrix of complex numbers.
This suggests that Jeffrey is secretly talking about a categorified
version of Heisenberg's "matrix mechanics" - and that's
true. I want to explain that. But I'm getting really sick of saying
"finite" and "finite-dimensional". So, henceforth
I'll leave out those adjectives... but they're really always there.
Okay?
Degroupoidification turns each groupoid into a vector space... but
in fact it gives more: a Hilbert space! Similarly, Jeffrey's process
actually turns each groupoid into a 2-Hilbert space. I proved that
a long time ago:
12) John Baez, Higher-dimensional algebra II: 2-Hilbert spaces,
Adv. Math. 127 (1997), 125-189. Also available as arXiv:q-alg/9609018.
So, just as degroupoidification reveals that a fair amount of quantum
mechanics can be done with groupoids instead of vector spaces,
Jeffrey's process reveals that a fair amount of categorified
quantum mechanics can also be done with groupoids!
Categorified quantum mechanics becomes important when we go from the
physics of particles (which is really field theory on 1d spacetimes)
to the physics of strings (which is really field theory on 2d
spacetimes). The simplest case is "topological string
theory", also known as "extended 2d topological quantum
field theory". And the simplest example of such a theory is the
"Dijkgraaf-Witten model": a gauge theory with a finite gauge
group.
In his thesis:
13) Jeffrey Morton, Extended TQFT's and Quantum Gravity, Ph.D.
thesis, U. C. Riverside, 2007. Available at arXiv:0710.0032.
Jeffrey showed that a special case, the "untwisted"
Dijkgraaf-Witten model, gives a weak 2-functor from the weak
2-category with
Composing this 2-functor with the 2-functor I just described,
he gets the untwisted Dijkgraaf-Witten model as an extended TQFT!
And in fact, he does it in all dimensions, not just dimension 2.
By the way, most of the 2-categories and 2-functors here are "weak".
Also by the way, Jeffrey constructed the above cobordism 2-category in
an earlier paper, which I discussed in "week242". He recently polished up this paper,
changing the title to make it focus on the algebraic essence of his
construction:
14) Jeffrey Morton, Double bicategories and double cospans,
available as arXiv:math/0611930.
There's a lot more I could say about this, but not a lot more time.
So, let me wrap up with a pointer to Stephen Summers' review of new
work on constructive quantum field theory.
Constructive quantum field theory is the branch of mathematical
physics where you try to rigorously construct examples of quantum
field theories. I did my Ph.D. thesis on this subject under Irving
Segal, but it was too hard for me, and my heart was never really in
it, so I soon fled - first to classical field theory, and then
further.
I recently met Stephen Summers at a conference in honor of von
Neumann, and he tried to call me back to my roots. It turns out
there's been a lot of interesting progress in constructive quantum
field theory! I'll probably keep working on topological quantum field
theory and other wimpy subjects - but it's great to hear someone out
there is doing the hard work of getting physically realistic quantum
field theories to make rigorous mathematical sense.
Here's some of what he has to say:
15) Stephen J. Summers, Constructive AQFT,
http://www.math.ufl.edu/~sjs/construction.html
Also check out his big AQFT page, which lists textbooks and
many more references:
16) Stephen J. Summers, Algebraic quantum field theory,
http://www.math.ufl.edu/~sjs/aqft.html
During the journey we commonly forget its goal. Almost every
profession is chosen as a means to an end but continued as an end in
itself. Forgetting our objectives is the most frequent act of
stupidity. - Friedrich Nietzsche
© 2008 John Baez


5
o---o
sits inside the A4 Coxeter group:
o---o---o---o
similarly the symmetries of a hexagon:
6
o---o
sit inside the A5 Coxeter group:
o---o---o---o---o
and so on: the noncrystallographic Coxeter groups I2(n)
sit nicely inside the Coxeter groups An+1. But the really
cool part is how deBruijn uses these to get quasiperiodic tilings of
the plane!

to the category with
I called this "degroupoidification". The idea is that a lot
of linear algebra has an underlying purely combinatorial
"skeleton" that doesn't involve the complex numbers - just
symmetry in its purest form. Groupoidification is quest to strip the
fat off linear algebra and do it using groupoids.
to the 2-category with
to the weak 2-category with
The development of the tools and techniques of algebraic quantum field
theory (AQFT) has reached the point where they can be turned upon the
question of existence of quantum field models. Although the program of
constructing models via AQFT is still in its infancy and only a few
researchers are working in the field, already some encouraging
successes can be displayed. I personally find it stimulating that the
ideas employed go well beyond the range of the semiclassical ideas
which were mathematically developed by researchers in constructive
quantum field theory in the 70's and 80's. There is no appeal to
Lagrangians, actions and perturbation theory, nor does one "work in
the Euclidean realm", and one generally avoids a direct construction
of strictly local quantum field operators (as these either do not
exist or are prohibitively difficult to construct), preferring to
construct more physically relevant quantities such as the scattering
amplitudes and local "observables". Some of the constructed models are
local and free, some are local and have nontrivial S-matrices, and yet
others manifest only certain remnants of locality, although these
remnants suffice to enable the computation of nontrivial two-particle
S-matrix elements. This includes models with nontrivial scattering in
four spacetime dimensions.
This is just the beginning of a fascinating review.
Check it out:
baez@math.removethis.ucr.andthis.edu

|
 
|

|