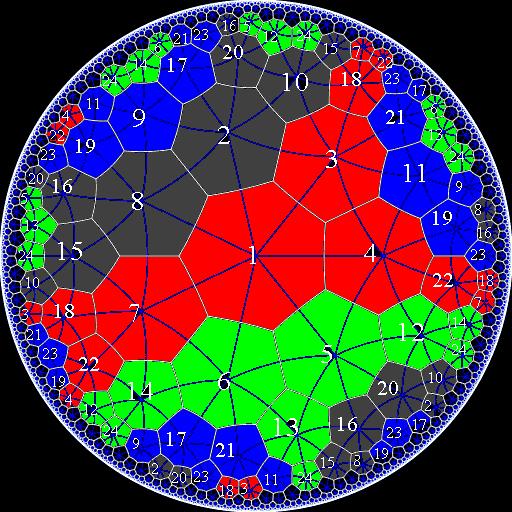
John Baez has a nice article on Klein's quartic. Early on in our discussion, I tried making one out of paper, but I reached a point where it looked too crumpled to illuminate the topology. Greg Egan made a movie of the dual of the heptagonal tiling, but we still haven't seen a good rendering of the original. Since there still seems to be some interest, here are pictures of my attempt. We start with one quarter of the surface:

Topologically, it's a disk with two holes and an outside edge, but it's clear there's trilateral symmetry. Here's the skeleton of this piece:
This piece corresponds to the grey heptagons:


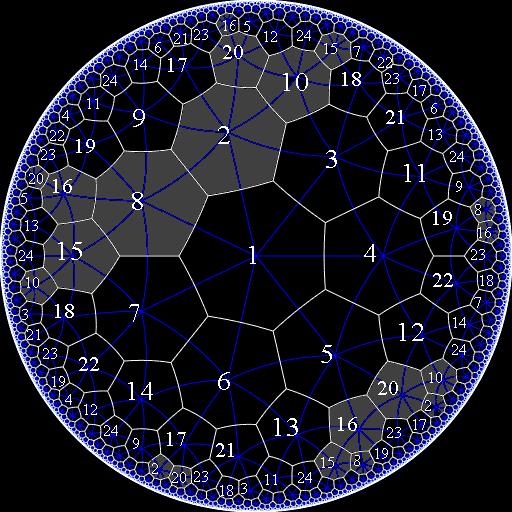
Now we join two of these pieces together to get half of the Klein quartic:

And here's its skeleton:

There are four heptagons on each piece that interlock with each other (where grey meets green).
10,20,16,15
12,5,13,24:


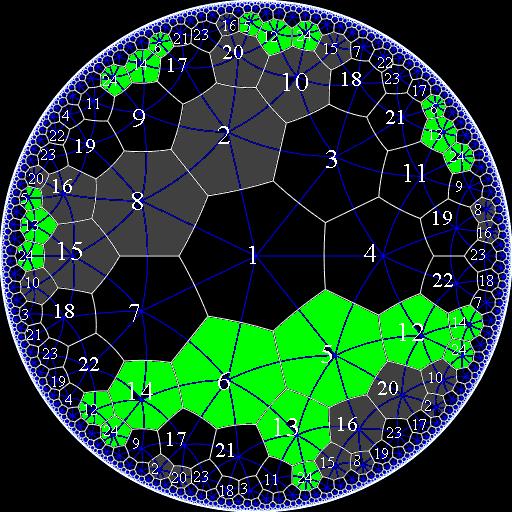
Now we add two more pieces to get all the heptagons (though we haven't connected all the edges yet):

The corresponding skeleton--

--curls up into a tetrahedron:

It's possible to make the paper model curl up like that, but it gets so crumpled that it's not worth taking a picture of. It should, however, illuminate the structure of Klein's quartic enough that you can match up the heptagons in this hyperbolic tiling to the ones made of paper: