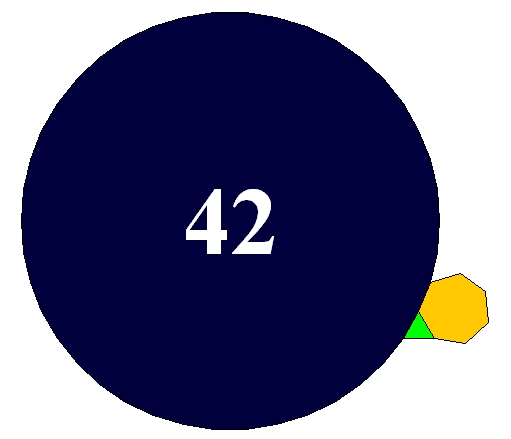
Let me reveal that now.
If you try to get several regular polygons to meet snugly at a point in the plane, what's the most sides any of the polygons can have? The answer is 42.
The picture shows an equilateral triangle, a regular heptagon and a regular 42-gon meeting snugly at a point. The reason this works is that \[ \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = \frac{1}{2} \] There are actually 10 solutions of \[ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} \] with \(p \le q \le r\), and each of them gives a way for three regular polygons to snugly meet at a point. But this particular solution features the biggest number of all!
But why is this so important? Well, it turns out that if you look for natural numbers \(a, b, c\) that make \[ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \] as close to 1 as possible, while still less than 1, the very best you can do is \(1/2 + 1/3 + 1/7\). It comes within \( 1/42 \) of equalling 1, since \[ \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = \frac{1}{2} \]
And why is this important? Well, suppose you're trying to make a doughnut with at least two holes that has the maximum number of symmetries. More precisely, suppose you're trying to make a Riemann surface with genus \(g \ge 2\) that has the maximum number of conformal transformations. Then you need to find a highly symmetrical tiling of the hyperbolic plane by triangles whose interior angles are \(\pi/a, \pi/b\) and \(\pi/c\), and you need \[ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \lt 1 \] for these triangles to fit on the hyperbolic plane.
For example, if you take \(a = 2, b = 3, c = 7\) you get this tiling:
_tiling.png)
A clever trick then lets you curl up the hyperbolic plane and get a Riemann surface with at most \[\displaystyle{ \frac{2(g-1)}{1 - \frac{1}{a} - \frac{1}{b} - \frac{1}{c}} } \] symmetries. So, you want to make \(1 - \frac{1}{a} - \frac{1}{b} - \frac{1}{c} \) as small as possible! And thanks to what I said, the best you can do is \[ \displaystyle{ 1 - \frac{1}{2} - \frac{1}{3} - \frac{1}{7} = \frac{1}{42} } \] So, your surface can have at most \[ 84(g-1) \] symmetries. This is called Hurwitz's automorphism theorem. The number 84 looks mysterious when you first see it — but it's there because it's twice 42.
But why is this stuff the answer to the ultimate question of life, the universe, and everything? I'm not sure, but I have a crazy theory. Maybe all matter and forces are made of tiny little strings! As they move around, they trace out Riemann surfaces in spacetime. And when these surfaces are as symmetrical as possible, reaching the limit set by Hurwitz's automorphism theorem, the size of their symmetry group is a multiple of 42, thanks to the math I just described.
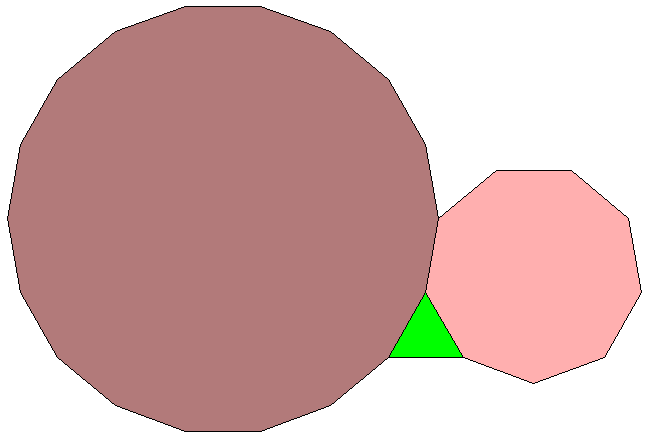
Puzzle 1. Consider solutions of \[ \displaystyle{ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} } \] with positive integers \(p \le q \le r,\) and show that the largest possible value of \(r\) is \(42\).
Puzzle 2. Consider solutions of \[ \displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < 1} \] with positive integers \( a, b, c,\) and show that the largest possible value of \( \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\) is \( 1 - \frac{1}{42}.\)
As for the first question, to get the most symmetrical Riemann surfaces, we should start with a tiling of the plane with triangles whose vertex angles are \(\pi/p\), \(\pi/q\) and \(\pi/r\) for some integers \(p,q,r\), and then cut out a portion and curl it up to form a \(g\)-holed torus. If you tile a \(g\)-holed torus with triangles like this, Euler's formula says \[ V - E + F = 2 - 2g \] where \(V\) is the number of vertices, \(E\) is the number of edges and \(F\) is the number of faces: that is, triangles. But \[ E = \frac{3}{2} F \] since each face has 3 edges, but 2 faces share each edge.
We can also figure out the number of vertices if we know the number of faces. You'll see in the pictue above that vertices come in three kinds: those where \(2 \times 2\) triangles meet, those where \(2 \times 3\) triangles meet, and those where \(2 \times 7\) triangles meet. That's how it's got to work for a highly symmetric tiling: there will be vertices where \(2 p\) triangles meet, vertices where \(2 q\) triangles meet, and vertices where \(2 r\) triangles meet. So, if you scratch your head and think a while, you'll see that \[ \displaystyle{ V = (\frac{1}{2p} + \frac{1}{2q} + \frac{1}{2r}) F } \]
Taking the last 3 equations I've written down and doing a little algebra, you can show \[ F = \displaystyle{\frac{4(g-1)}{1 - \frac{1}{p} - \frac{1}{q} - \frac{1}{r}} } \] So, this is the number of triangles. But in the most symmetrical situations, there's a symmetry sending any triangle to any other! That takes work to show... but the upshot is that at least for \(g \ge 2\), the most symmetrical Riemann surfaces have \[ \displaystyle{\frac{4(g-1)}{1 - \frac{1}{p} - \frac{1}{q} - \frac{1}{r}} } \] symmetries for some positive integers \(p,q,r\).
To make this number of symmetries as big as possible, we need to make \[ \displaystyle{1 - \frac{1}{p} - \frac{1}{q} - \frac{1}{r} } \] as small as possible (while still being positive). And now for the magic part! To make this number as small as possible we need to use \( p = 2, q = 3, r = 7\): \[ \displaystyle{1 - \frac{1}{2} - \frac{1}{3} - \frac{1}{7} = \frac{1}{42} } \] You can check this by considering all the different options in a systematic way — it's a great exercise if you're ever stuck on a long bus ride. So, we get a maximum of \[ 42 \times 4(g -1 ) = 168 (g - 1) \] symmetries! But these symmetries include reflections; if we disallow those, as usually done in stating Hurwitz's theorem, we get half as many: \[ 84 (g - 1) \]
As for the second question: we can't always find a \(g\)-holed Riemann surface with \(84(g-1)\) conformal transformations.
The first time we reach the maximum is when our surface has 3 holes. Starting in 1878, Felix Klein studied the most symmetrical Riemann of this sort, and he showed it has \(84 \times 2 = 168\) symmetries. It's a really amazing thing, called Klein's quartic curve. Here's a picture, made by Greg Egan:

If you carefully count the triangles in the picture above, you'll get 56. However, these triangles are equilateral, or at least they would be if we could embed Klein's quartic curve in 3d space without distorting it. If we drew all the smaller triangles whose interior angles are \(\pi/2, \pi/3\) and \(\pi/7\), each equilateral triangle would get subdivided into 6 smaller ones, and there would be a total of \( 6 \times 56 = 336 \) of these. But \[ 336 = 8 \times 42 \] Half of these smaller triangles are 'left-handed' and half are 'right-handed'. There's a conformal transformation sending a chosen triangle to any other triangle of the same handedness, for a total of \[ 168 = 4 \times 42 \] transformations.
The next case where we get the maximum number of symmetries is the 7-holed torus. This can be given a complex structure whose that admits \(504 = 84 \times 6\) conformal transformations. This is called the Fricke–Macbeath curve, discovered by Fricke in 1899.
The next case is the 14-holed torus, which can be given three different complex structures with 1092 = 84 × 13 symmetries. These are called the first Hurwitz triplet.
This is the start of a complicated and interesting subject. For more details, see my page on Klein's quartic curve.
Sums of reciprocals of natural numbers are called 'Egyptian fractions', and they have deep connections to geometry; for more on this see my article on Archimedean tilings and Egyptian fractions.
The picture of a triangle, heptagon and 42-gon was made by Tyler, and you can see all 10 ways to get 3 regular polygons to meet snugly at a vertex on Wikipedia. Of these, only 11 can occur in a uniform tiling of the plane. The triangle, heptagon and 42-gon do not tile the plane, but you can see some charming attempts to do something with them on Kevin Jardine's website Imperfect Congruence:
You can read more about all these things in the slides of a public lecture I gave at the Canadian Mathematical Society winter meeting in 2005:
Puzzle 1. Consider solutions of
\[ \displaystyle{ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} } \]
with positive integers \(p \le q \le r,\) and show that the largest possible value of \(r\) is \(42\).
Answer. We will systematically go through positive integers \(p
\le q\) with \( \frac{1}{p} + \frac{1}{q} \lt \frac{1}{2}\), working
our way up from small integers to big ones, so that \( \frac{1}{p} +
\frac{1}{q}\) decreases, forcing \(\frac{1}{r}\) to get bigger and
thus forcing \(r\) to go down.
Puzzle 2. Consider solutions of
\[ \displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < 1} \]
with positive integers \( a, b, c,\) and show that the largest
possible value of \( \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\) is
\( 1 - \frac{1}{42}.\)
Answer. The same sort of approach works here. We can assume
\(a \le b \le c\).
Text © 2015 John Baez
And so on: it's all downhill from here. The solutions we've found gives ways to make 3 regular polygons meet snugly at a vertex:


 If you want a harder puzzle, you can march on and figure out
all the solutions of \[ \displaystyle{ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} } \]
There are 10, not counting permutations of \(p,q\) and \(r\).
If you want a harder puzzle, you can march on and figure out
all the solutions of \[ \displaystyle{ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} } \]
There are 10, not counting permutations of \(p,q\) and \(r\).
Each solution of
\[ \displaystyle{ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < 1} \]
with positive integers \(a,b,c\) gives a tiling of hyperbolic space by
triangles whose interior angles are \(\pi/a, \pi/b\) and \(\pi/c\). There
are infinitely many solutions, but we have found the three 'flattest' ones,
meaning that the triangles are closest to Euclidean: their interior angles
add up to almost \(\pi\):
There is a lot one can do with these tilings, starting here.
_tiling.png)
_tiling.png)
_tiling.png)
"Good Morning," said Deep Thought at last.
"Er...good morning, O Deep Thought" said Loonquawl nervously, "do you have...er, that is..."
"An Answer for you?" interrupted Deep Thought majestically. "Yes, I have."
The two men shivered with expectancy. Their waiting had not been in vain.
"There really is one?" breathed Phouchg.
"There really is one," confirmed Deep Thought.
"To Everything? To the great Question of Life, the Universe and everything?"
"Yes."
Both of the men had been trained for this moment, their lives had been a preparation for it, they had been selected at birth as those who would witness the answer, but even so they found themselves gasping and squirming like excited children.
"And you're ready to give it to us?" urged Loonsuawl.
"I am."
"Now?"
"Now," said Deep Thought.
They both licked their dry lips.
"Though I don't think," added Deep Thought. "that you're going to like it."
"Doesn't matter!" said Phouchg. "We must know it! Now!"
"Now?" inquired Deep Thought.
"Yes! Now..."
"All right," said the computer, and settled into silence again. The two men fidgeted. The tension was unbearable.
"You're really not going to like it," observed Deep Thought.
"Tell us!"
"All right," said Deep Thought. "The Answer to the Great Question..."
"Yes...!"
"Of Life, the Universe and Everything..." said Deep Thought.
"Yes...!"
"Is..." said Deep Thought, and paused.
"Yes...!"
"Is..."
"Yes...!!!...?"
"Forty-two," said Deep Thought, with infinite majesty and calm. - Douglas Adams, The Hitchhiker's Guide to the Galaxy
Images copyrighted by those who made them.
baez@math.removethis.ucr.andthis.edu
home