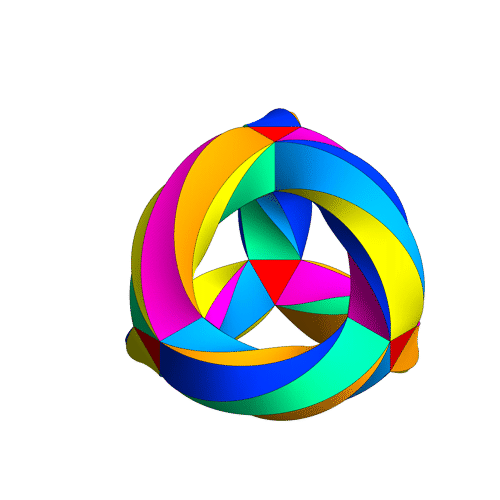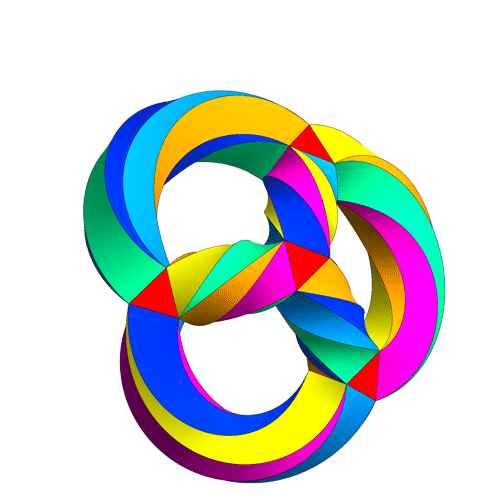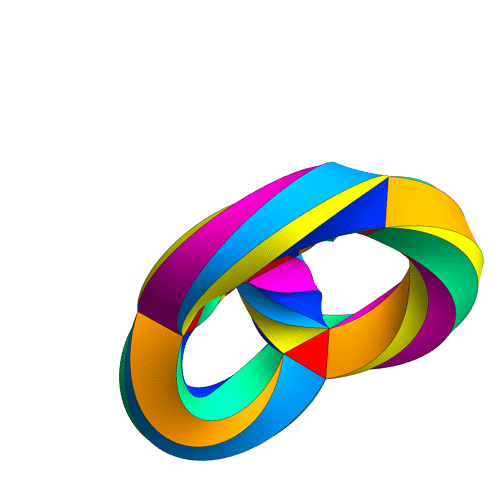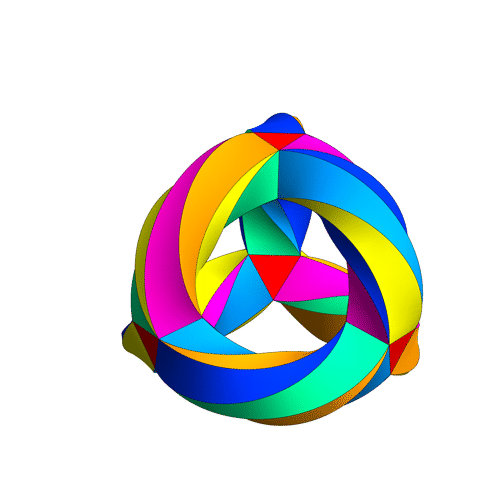
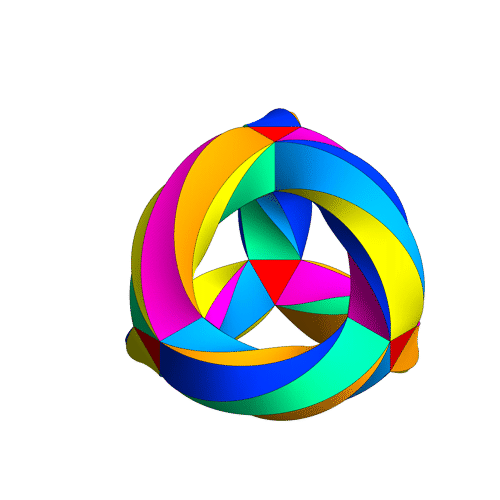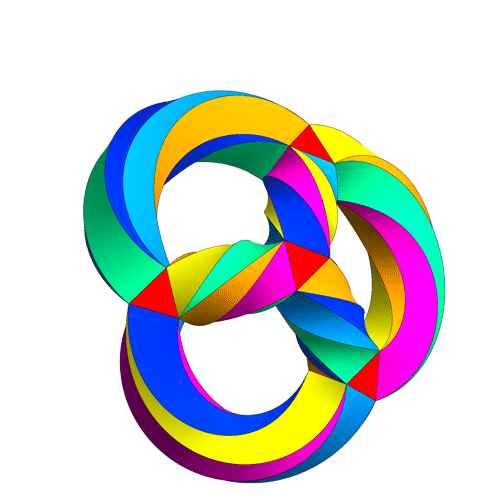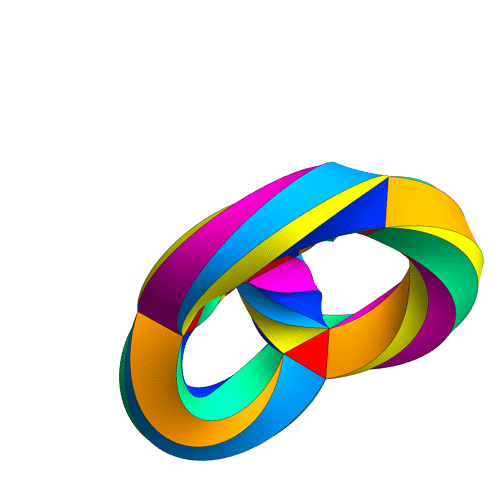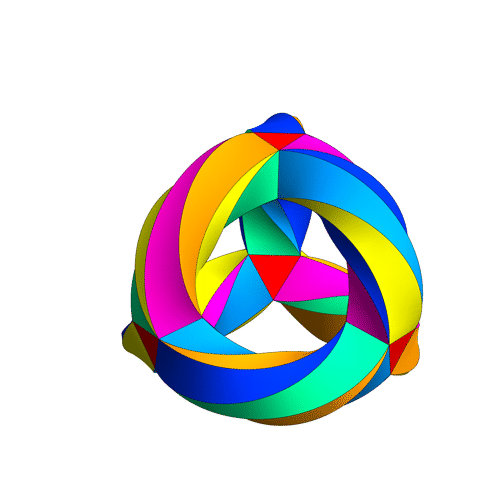
This is a movie of Klein's quartic turning itself inside out, made Greg Egan.
Beautiful, eh? But to understand what's it's really about, let's back up and start at the beginning...
Take a bunch of equilateral triangles. Glue them together so that 3 meet at each corner. You get a regular tetrahedron:
Then take a bunch of squares. Glue them together so that 3 meet at each corner. You get a cube:
Next, take a bunch of regular pentagons. Glue them together so that three meet at each corner. You get a regular dodecahedron:
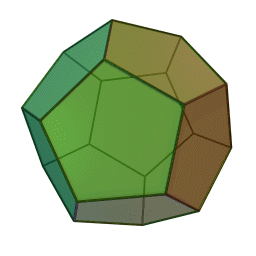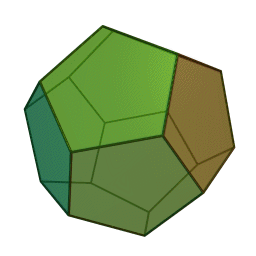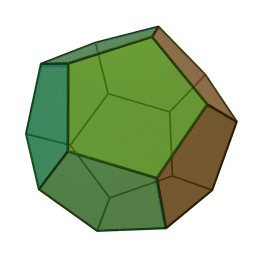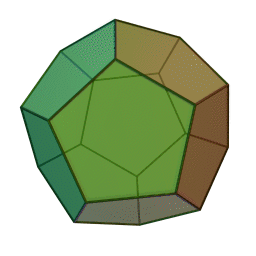
This is fun! We're getting a series of Platonic solids.
Next, take a bunch of regular hexagons and glue them together so that three meet at each corner. Now the angles of the hexagons add up to 360 degrees, so we don't get a Platonic solid. Instead, we get a tiling of the plane. It looks like a honeycomb that stretches out forever in all directions:

But, if you want something finite in size, you can cut out a portion of this honeycomb and curl it up to get a doughnut, or torus. There are actually lots of ways to do this. You might have fun figuring out what they all are. Can you take just one regular hexagon and curl it up to form a torus?
Anyway, these tori deserve to be called "Platonic surfaces", since they are surfaces tiled with regular polygons, with the same number meeting at each vertex.
Next, let's take a bunch of regular heptagons and glue them together so that three meet each corner. Now the angles add up to more than 360 degrees, so we get a tiling of the "hyperbolic plane". The hyperbolic plane is like the opposite of a sphere, since it's saddle-shaped at every point instead of bulging out at every point. In fact the sphere and the hyperbolic plane are the two most symmetrical forms of non-Euclidean geometry. The sphere is "positively curved", while the hyperbolic plane is "negatively curved".
You may have trouble visualizing the hyperbolic plane tiled with regular heptagons, but if we distort it, it fits into a disk and looks really pretty! Don Hatch has drawn a nice picture of it:
It's called "{7,3}", since it's made of 7-sided figures with 3 meeting at each corner.
In this picture there's one heptagon at the center, surrounded by rings of heptagons that appear smaller (but aren't really: that's just an effect of the distortion).
Can we cut out a portion of this tiling and curl it up to get a torus? No! But we can curl up a portion to get a 3-holed torus — like the surface of a doughnut with three holes. However, we can only do this if we use precisely 24 heptagons! The result is called Klein's quartic.
Klein's quartic is an amazingly symmetrical thing: it has 336 symmetries if we include reflections, or half that many — 168 — if we don't. These numbers look pretty weird, but have you ever heard someone say they're working "24-7"? That is, 24 hours a day, 7 days a week? Well, \[ 24 \times 7 = 168 \] so there are 168 hours in a week, and 336 hours in a fortnight. Surely this is an irrelevant coincidence — though it should help you remember these numbers. What really matters is that Klein's quartic has 24 heptagons, and there's a symmetry sending your favorite heptagon to any of these 24, but it can also be rotated 7 ways, for a total of 168 symmetries... or twice as many if we also allow it to be reflected.
Exactly how do you curl up the hyperbolic plane to get Klein's quartic? You need to make sure all the heptagons with the same numbers here get glued together:
(The numbers here were drawn by Mike Stay on top of Don Hatch's picture.)
Unfortunately, it's pretty hard to visualize the result of this procedure! You can check mathematically that you get a 3-holed torus, but it's impossible to embed this surface in 3d Euclidean space without either warping it or doing some other funky maneuvers, as shown here:
So... let's warp it! It's actually easier to start with a tiling of the hyperbolic plane by equilateral triangles, with 7 meeting at each vertex:
Unsurprisingly, this tiling is called "{3,7}". It has the same symmetries as our friend {7,3}, and indeed you can still see the heptagons in blue. We say that {7,3} and {3,7} are "Poincaré duals" of each other, just like the cube and octahedron.
If we curl up this thing correctly, we get a 3-holed torus tiled by 56 triangles (or dually, by 24 heptagons). If you try to make a paper model this way, the result is inevitably a big mess. To see what I mean, try Mike Stay's webpage, where he wisely stops just short of completing the task — and Gerard Westendorp's page, where he succeeds in finishing the job by using pastry instead of paper!
There might be a small market for Klein quartic birthday cakes, but for visualizing the quartic, computer graphics are better:

Voilà!
The above picture was created a long time ago by Joe Christy, using a program called Geomview, which creates virtual 3d objects. It took about a day on the fastest Linux machine they had at the time. The advantage of Geomview is that it lets you easily see different views:


Felix Klein originally built his surface in a different way. In his original 1879 paper he drew a surface tiled by 24 heptagons, together with directions for how to create a 3-holed torus by attaching the sides of this surface to each other. I found this color version on Tony Smith's website:

You'll notice the heptagons are drawn in a fancy style: each one has been "barycentrically subdivided" into 14 little right triangles. But don't worry about those yet — concentrate on the heptagons!
There's a blue heptagon in the middle, 7 red ones touching that, 7 yellow ones touching those, then 7 green ones falling off the edge of the picture, and 2 blue ones broken into bits all around the corners of the picture. That's a total of 24 heptagons.
We wrap this thing up into a 3-holed torus using the numbers on the edges of the picture:
In other words, connect edges 2n+1 and 2n+6 mod 14. To connect them the right way, make sure that triangles of the same color never touch each other.
Here's how to see if you've done it right. Ignore the little triangles; just pay attention to the heptagons! Then:
Start on any edge of any heptagon and march along in either direction.
When you get to the end, turn left.
When you get to the end, turn right.
When you get to the end, turn left.
When you get to the end, turn right.
When you get to the end, turn left.
When you get to the end, turn right.
When you get to the end, turn left.
When you get to the end, turn right.
You should now be back where you started!
These are like the devil's driving directions to people who ask the way out of hell: LRLRLRLR and you'll be right back!
Hellish driving directions... but the Klein quartic is heavenly. As I said, it's incredibly symmetrical.
To better understand its symmetries. let's count those little right triangles in the picture above. Since the picture shows 24 heptagons, each chopped into 14 right triangles, the total number of right triangles is \[ 24 \times 14 = 336 \] Hey! This is precisely the number of symmetries of the Klein quartic, including reflections!
This is no coincidence. We can specify a symmetry by saying where it sends our favorite right triangle. Since it can go to any other triangle, there are 336 possibilities. If we exclude reflections, we get half as many symmetries: 24 × 7 = 168.
By the way, this trick works for ordinary Platonic solids as well. For example, if we take a dodecahedron and barycentrically subdivide all 12 pentagons, we get 10 × 12 = 120 right triangles. If we pick one of these as the "identity element", we can specify any symmetry by saying which triangle this triangle gets sent to. So, the set of triangles becomes a vivid picture of the 120-element rotation/reflection symmetry group of the dodecahedron. This idea generalizes in many directions, and is incredibly useful.
Now let's see if we can visualize the 24×7-fold symmetry of Klein's quartic, not counting rotations. The 7-fold symmetry is easiest to visualize as rotations of Klein's original picture:

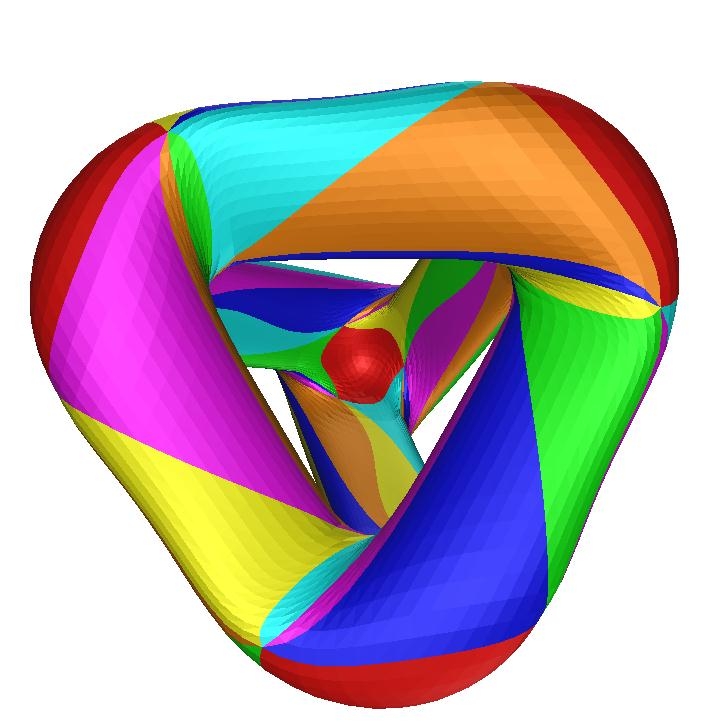
The 24-fold symmetry is a bit harder to see. A tetrahedron has 12 rotational symmetries, and it's easy to see these here:

This wonderful picture was drawn by Greg Egan with the help of ideas from Mike Stay and Gerard Westendorp. It's probably the best way for a nonmathematician to appreciate the symmetry of Klein's quartic. It's a 3-holed torus, but drawn in a way that emphasizes the tetrahedral symmetry lurking in this surface! You can see there are 56 triangles: 2 for each of the tetrahedron's 4 corners, and 8 for each of its 6 edges.
However, 12 is just half of 24, so there should be an extra 2-fold symmetry, besides the 12 rotational symmetries of the tetrahedron. And there is! It consists of twisting Klein's quartic inside out, like this:
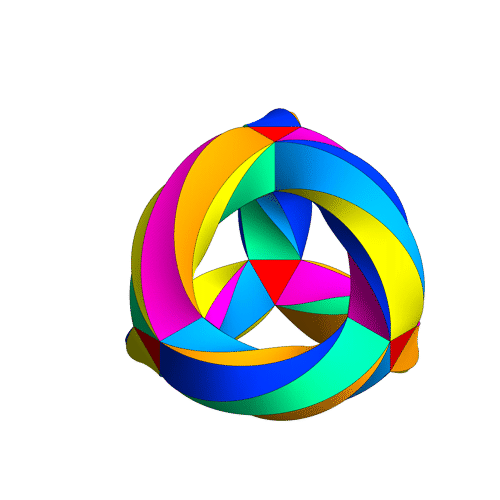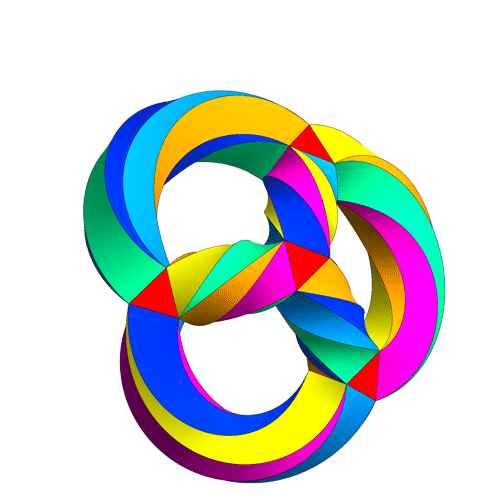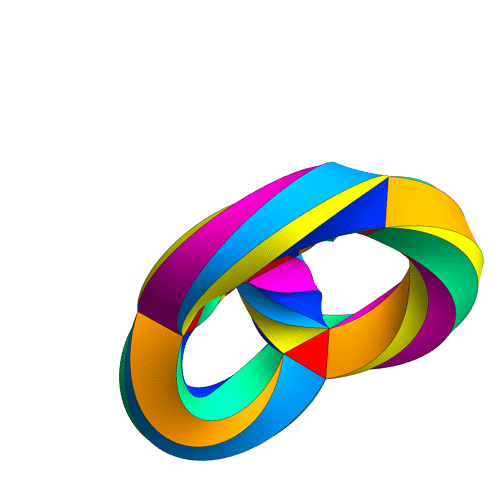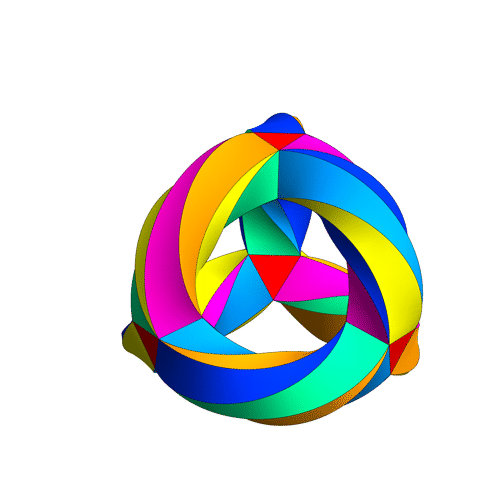
Isn't that cool?
Klein's quartic has many other charms. For example, if we take our hyperbolic plane tiled with heptagons and count them grouped according to how far they are from the central one, we get this sequence: \[ 7, 7, 14, 21, 35, 56, 91, \dots \]
7 times the Fibonacci numbers!
To dig deeper, though, it helps to think about complex analysis. If we think of the hyperbolic plane as the unit disc in the complex plane, this surface becomes a "Riemann surface", meaning that it gets equipped with a complex structure. This was Felix Klein's viewpoint when he first discovered this stuff. He showed that his surface could be described by an incredibly symmetrical quartic equation in 3 complex variables: \[ u^3 v + v^3 w + w^3 u = 0 \]
where we count two solutions as the same if they differ by an overall factor. So, his surface is called "Klein's quartic curve".
Why is it called a "curve" and not a surface? Because it takes one complex number to say where you are on it. We have 3 unknowns and one equation, but we mod out by an overall factor, so we get something locally parametrized by one complex number... so algebraic geometers call it a curve. Ordinary people find that confusing.
Anyway, Klein proved that his surface was a 3-holed torus, and that it can be tiled by 24 regular heptagons just as we have described above. His proof is not very easy; you can see a simpler one on Greg Egan's website.
You can read Klein's original article translated into English as part of a whole free online book on Klein's quartic curve:
This book was put out by the Mathematical Sciences Research Institute in Berkeley to celebrate the completion of sculpture of Klein's quartic curve made by Helaman Ferguson. I must admit that the sculpture leaves me unmoved. But the curve itself — ah, that's another story! It's great.
Mathematically, Klein's quartic curve is special because it has the maximum number of symmetries of any 3-holed Riemann surface.
By "Riemann surface", I mean a surface equipped with a way of measuring angles. For an oriented surface, like a 3-holed torus, this is the same as a smoothly varying way to rotate tangent vectors 90 degrees counterclockwise. We can think of this as a way to multiply these vectors by √-1 — in other words, a "complex structure". Thus, we can do complex analysis on any Riemann surface. Locally, it might as well be the complex plane.
To understand the theme of incredibly symmetrical Riemann surfaces, let's first consider a Riemann surface with no holes: a sphere. There's only one way to make a sphere into a Riemann surface - it's called the Riemann sphere. You can think of it as the complex numbers plus a point at infinity. This has infinitely many symmetries. They're called conformal transformations, and they all look like this: \[ z \mapsto \frac{a z + b}{c z + d} \] They form a group called \(\mathrm{PSL}(2,\mathbb{C})\), since it's the same as the group of 2×2 complex matrices with determinant 1, mod scalars. It's also the same as the Lorentz group, famous in special relativity!
There are different ways to make a torus into a Riemann surface, some with more symmetries than others (see "week124" of my column). But, there are always translation symmetries in both directions, so the symmetry group is always infinite.
On the other hand, a Riemann surface with 2 or more holes can only have a finite group of conformal transformations. In fact, in 1893 Hurwitz proved that a Riemann surface with \(g \ge 2\) holes has at most \[ 84(g - 1) \] conformal transformations (not including reflections). When \(g = 3\), this is 168. So, Klein's quartic curve is as symmetrical as a 3-holed torus can possibly be!
The appearance of the number 84 in Hurwitz's theorem is pretty shocking at first. Why does such a weird number show up in such a fundamental result?
It's because to get the most symmetrical Riemann surfaces, we should start with a tiling of the plane with triangles whose vertex angles are \(\pi/p\), \(\pi/q\) and \(\pi/r\) for some integers \(p,q,r\), and then cut out a portion and curl it up to form a \(g\)-holed torus. For example, to get Klein's quartic curve we take \( p = 2, q = 3, r = 7\):
_tiling.png)
If you tile a \(g\)-holed torus with triangles like this, Euler's formula says \[ V - E + F = 2 - 2g \] where \(V\) is the number of vertices, \(E\) is the number of edges and \(F\) is the number of faces: that is, triangles. But \[ E = \frac{3}{2} F \] since each face has 3 edges, but 2 faces share each edge.
We can also figure out the number of vertices if we know the number of faces. You'll see in the pictue above that vertices come in three kinds: those where \(2 \times 2\) triangles meet, those where \(2 \times 3\) triangles meet, and those where \(2 \times 7\) triangles meet. That's how it's got to work for a highly symmetric tiling: there will be vertices where \(2 p\) triangles meet, vertices where \(2 q\) triangles meet, and vertices where \(2 r\) triangles meet. So, if you scratch your head and think a while, you'll see that \[ \displaystyle{ V = (\frac{1}{2p} + \frac{1}{2q} + \frac{1}{2r}) F } \]
Taking the last 3 equations I've written down and doing a little algebra, you can show \[ F = \displaystyle{\frac{4(g-1)}{1 - \frac{1}{p} - \frac{1}{q} - \frac{1}{r}} } \] So, this is the number of triangles. But in the most symmetrical situations, there's a symmetry sending any triangle to any other! That takes work to show... but the upshot is that at least for \(g \ge 2\), the most symmetrical Riemann surfaces have \[ \displaystyle{\frac{4(g-1)}{1 - \frac{1}{p} - \frac{1}{q} - \frac{1}{r}} } \] symmetries for some positive integers \(p,q,r\).
To make this number of symmetries as big as possible, we need to make \[ \displaystyle{1 - \frac{1}{p} - \frac{1}{q} - \frac{1}{r} } \] as small as possible (while still being positive). And now for the magic part! To make this number as small as possible we need to use \( p = 2, q = 3, r = 7\): \[ \displaystyle{1 - \frac{1}{2} - \frac{1}{3} - \frac{1}{7} = \frac{1}{42} } \] You can check this by considering all the different options in a systematic way — it's a great exercise if you're ever stuck on a long bus ride. So, we get a maximum of \[ 42 \times 4(g -1 ) = 168 (g - 1) \] symmetries! But these symmetries include reflections; if we disallow those, as usually done in stating Hurwitz's theorem, we get half as many: \[ 84 (g - 1) \] So, we see that far from being arbitrary flukes, the numbers 84 and 168 are burnt deep into the fabric of reality.
Sitting inside \(\mathrm{PSL}(2,\mathbb{Z})\) is a group called \(\Gamma(7)\), consisting of guys where each entry of the matrix \[ \left( \begin{array}{cc} a & b \\ c & d \end{array}\right) \] is congruent to the corresponding entry of the identity matrix \[ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \] modulo 7. This is an example of a "congruence subgroup"; these serve to relate complex analysis to number theory in lots of cool ways. In particular, Klein's quartic curve is just \[ \mathbb{H}/\Gamma(7) \] Since \(\Gamma(7)\) is a normal subgroup of \(\mathrm{PSL}(2,\mathbb{Z})\), the quotient group \[ \mathrm{PSL}(2,\mathbb{Z})/\Gamma(7) = \mathrm{PSL}(2,\mathbb{Z}/7) \] acts as symmetries of Klein's quartic curve. And, this group has 168 elements!
This group doesn't include reflection symmetries, since they don't preserve the complex structure — they're like complex conjugation. If we include them, we get a 336-element group called \(\mathrm{PGL}(2,\mathbb{Z}/7)\).
In fact, \(\mathrm{PSL}(2,\mathbb{Z}/7)\) is the second smallest nonabelian simple group. The smallest one is the rotational symmetry group of the icosahedron, which has 60 elements. This group is actually \( \mathrm{PSL}(2,\mathbb{Z}/5)\), and Klein had run into it in his work on the icosahedron and quintic equations. So, it's actually far from sheer luck that he then moved on to \( \mathrm{PSL}(2,\mathbb{Z}/7)\) and ran into his wonderful quartic curve.
By the way, this 168-element group is also known as \(\mathrm{PSL}(3,\mathbb{Z}/2)\) — the symmetries of the "Fano plane". This is another name for the projective plane over Z/2. It has 7 points and 7 lines, with 3 points on each line and 3 lines through each point. If you draw one of the lines as a circle, it looks like this picture from the Wikipedia article on finite geometries:
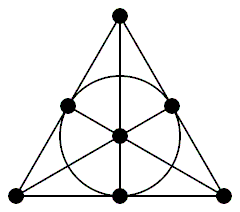
A symmetry of the Fano plane is any function from points to points that sends lines to lines. Such symmetries can send any point to any other point, and even while not moving one point they can permute the 4 lines not containing that point in an arbitrary way, for a total of \[ 4! \times 7 = 168 \] symmetries.
The 7-fold symmetry of the Fano plane is visible in this picture drawn by Burkard Polster, author of Geometries on Surfaces and The Mathematics of Juggling:
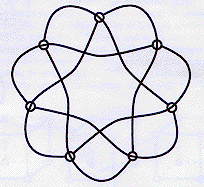
The 24-fold tetrahedral symmetry of the Fano plane is best seen by drawing 4 of its lines as circles and the rest as actual lines, like this:
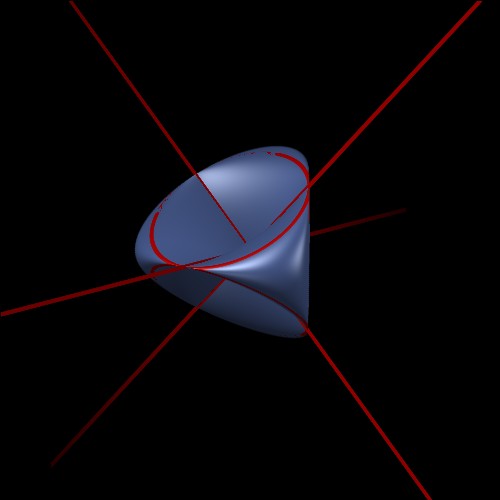
This picture was drawn by Joe Christy. Here the points of the Fano plane are seen as singular points of the real part of a surface which is called the Roman surface because the mathematician who discovered it was in Rome at the time.
This surface probably deserves a webpage of its own....
But now let's think harder about the symmetries of Klein's quartic curve and why they match those of the Fano plane.
First, there's the obvious 7-fold symmetry of Klein's original picture, which matches the 7-fold symmetry of Burkhard Polster's picture of the Fano plane:

There are some subtleties. For example, rotating the central blue heptagon also has the effect of rotating each of the two blue heptagons near the edges. If you rotate the central heptagon 1/7 of a turn, one of the other heptagons rotates 2/7 of a turn and the other rotates 4/7 of a turn. Since 8/7 of a turn is the same as 1/7 of a turn, we can say there are 3 heptagons rotating, each twice as fast as the previous one! Greg Egan has made a movie of this in the Poincare dual picture where the Klein quartic is tiled by 56 triangles:
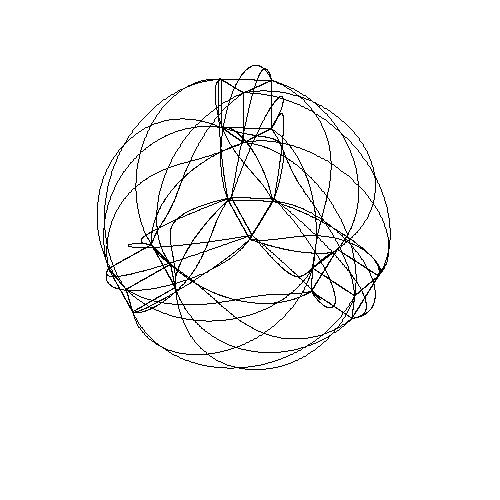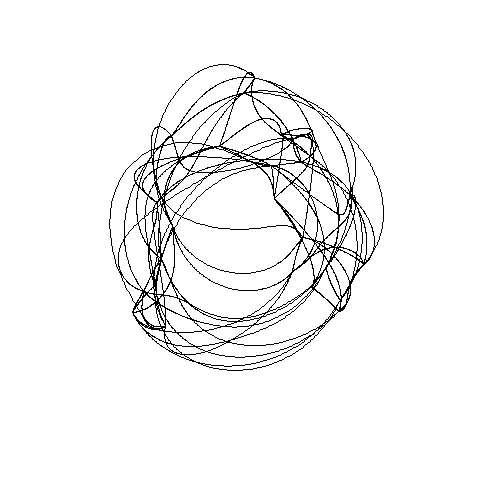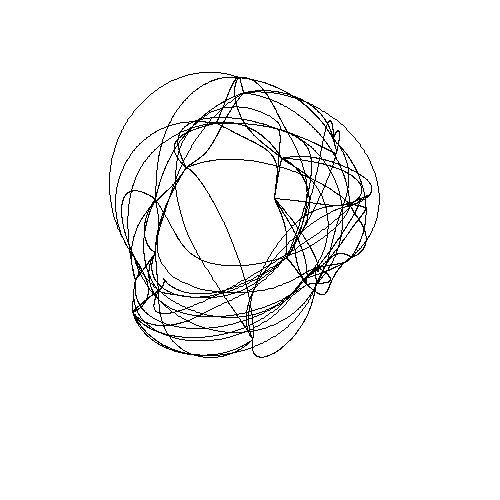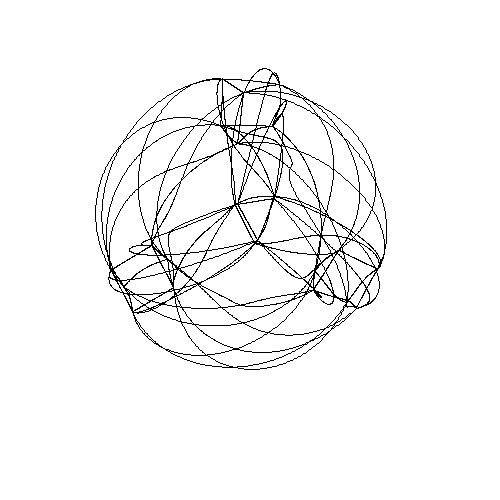
If you look carefully you'll see three 7-valent vertices rotating around.
Second, there's the obvious 12-fold rotational symmetry of Egan's tetrahedral picture:

together with this extra 2-fold symmetry:
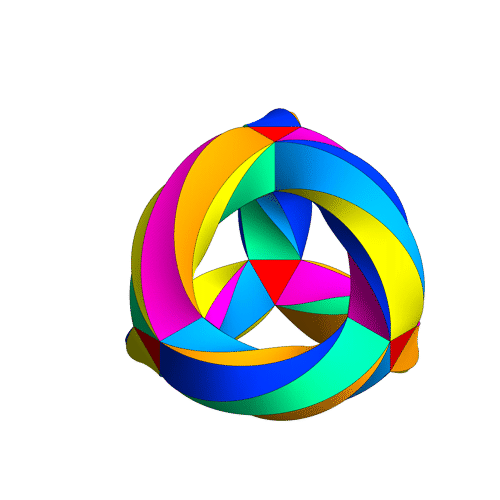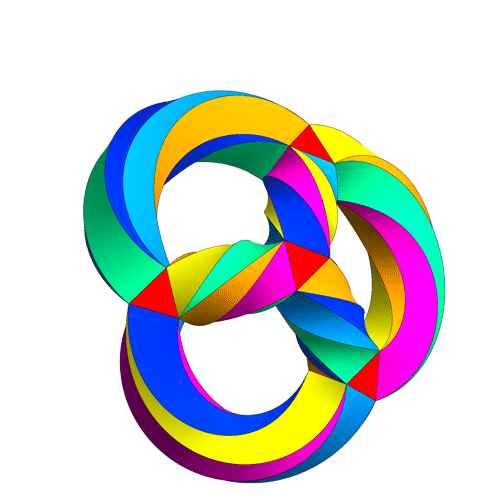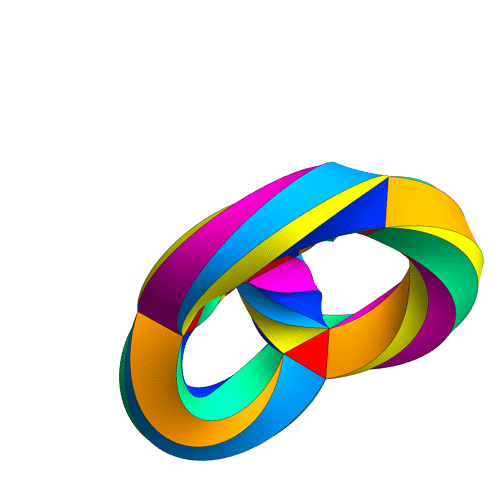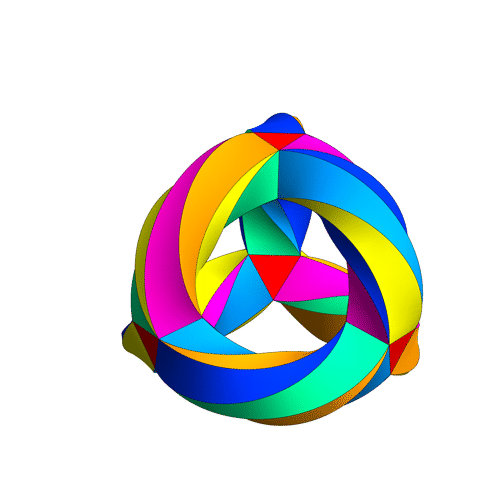
These fit together to give a 24-fold symmetry of Klein's quartic curve.
In fact, if you watch carefully, you'll see that the tetrahedron gets reflected as it turns inside out in Egan's movie. More precisely, if you follow the four corners of the tetrahedron, you'll see that two come back to where they were, while the other two get switched. So, this symmetry acts as a reflection, or odd permutation, of the 4 corners. The rotations act as even permutations of the corners.
So, these 24 symmetries form a group isomorphic to the rotation/reflection symmetry group of a tetrahedron. Algebraically speaking, this group is S4: the permutations of 4 things. These match the 24 permutations of 4 lines not going through a given point in the Fano plane.
But S4 has another significance, as well: it's the rotational symmetry group of a cube. And Egan was able to spot a hidden cube lurking in his picture! Can you?

If you look carefully, you'll see each corner of his tetrahedral gadget is made of a little triangular prism with one triangle facing out and one facing in: for example, the pink triangle staring you right in the face, or the light blue one on top. Since 4 × 2 = 8, there are 8 of these triangles. Abstractly, we can think of these as the 8 corners of a cube! They aren't really, but we can pretend. The way these 8 triangles come in pairs corresponds to how the vertices of a cube come in diagonally opposite pairs.
Using this, you can see that the group S4 acts on these 8 triangles in precisely the same way it acts via rotations on the vertices of a cube.
In fact, you can even draw a picture of a cube on the Klein quartic by drawing suitable curves that connect the centers of these 8 triangles! It's horribly distorted, but topologically correct. Part of the distortion is caused by embedding the Klein quartic in ordinary 3d Euclidean space. If we gave the Klein quartic the metric it inherits from the hyperbolic plane, the edges of the cube would be geodesics.
This remark also helps us see something else. The Klein quartic is tiled by 56 triangles. 8 of them give the cube we've just been discussing. In Egan's picture these triangles look special, since they lie at the corners of his tetrahedral gadget. But this is just an illusion caused by embedding the Klein quartic in 3d space. In reality, the Klein quartic is perfectly symmetrical: every triangle is just like every other. So in fact there are lots of these cubes, and every triangle lies in some cube.
But this is where it gets really cool. In fact, each triangle lies in just one cube. So, there's precisely one way to take the 56 triangles and divide them into 7 bunches of 8 so that each bunch forms a cube.
So: the symmetry group of the Klein quartic acts on the set of cubes, which has 7 elements.
But as I explained last week, this symmetry group also acts on the Fano plane, which has 7 points.
This suggests that cubes in the Klein quartic naturally correspond to points of the Fano plane. And Egan showed this is true!
He showed this by showing more. The Fano plane also has 7 lines. What 7 things in the Klein quartic do these lines correspond to?
Anticubes!
You see, the cubes in the Klein quartic have an inherent handedness to them. You can go between the 8 triangles of a given cube by following certain driving directions, but these driving directions involve some left and right turns. If you follow the mirror-image driving directions with "left" and "right" switched, you'll get an anticube.
Apart from having the opposite handedness, anticubes are just like cubes. In particular, there's precisely one way to take the 56 triangles and divide them into 7 bunches of 8 so that each bunch forms an anticube.
Here's a picture of the 7 cubes and 7 anticubes, drawn Greg Egan:
Each triangle has a colored circle and a colored square on it. There are 7 colors. The colored circle says which of the 7 cubes the triangle belongs to. The colored square says which of the 7 anticubes it belongs to.
If you stare at this picture for a few hours, you'll see that each cube is completely disjoint from precisely 3 anticubes. Similarly, each anticube is completely disjoint from precisely 3 cubes.
This is just like the Fano plane, where each point lies on 3 lines, and each line contains 3 points!
So, we get a vivid way of seeing how every figure in the Fano plane corresponds to some figure in the Klein quartic curve. This is why they have the same symmetry group.
This is an excellent example of Felix Klein's "Erlangen program" for reducing geometry to group theory. We are beginning to see how two superficially different geometries are secretly the same:
| FANO PLANE | KLEIN'S QUARTIC CURVE |
|---|---|
| 7 points | 7 cubes |
| 7 lines | 7 anticubes |
| incidence of points and lines | disjointness of cubes and anticubes |
| KLEIN'S QUARTIC CURVE | FANO PLANE |
|---|---|
| 24 vertices | ??? |
| 84 edges | ??? |
| 56 triangular faces | ??? |
| incidence of vertices and edges | ??? |
| incidence of edges and faces | ??? |
For now, let me give the precise driving directions that define a "cube" or an "anticube" in Klein's quartic curve. Say you're on some triangle and you want to get to a nearby triangle that belongs to the same cube. Here's what you do:
hop across any edge,Or, suppose you're on some triangle and you want to get to another that's in the same anticube. Here's what you do:
turn right,
hop across the edge in front of you,
turn left,
then hop across the edge in front of you.
hop across any edge,(If you don't understand this stuff, look at the picture above and see how to get from any circle or square to any other circle or square of the same color.)
turn left,
hop across the edge in front of you,
turn right,
then hop across the edge in front of you.
You'll notice that these instructions are mirror-image versions of each other. They're also both 1/4 of the "driving directions from hell" that I described earlier. In other words, if you go LRLRLRLR or RLRLRLRL, you wind up at the same triangle you started from. You'll have circled around one face of a cube or anticube!
In fact, your path will be a closed geodesic on the Klein quartic curve... precisely like this long dashed line in Klein's original picture:

For more, you should look at Greg Egan's pages about Klein's quartic curve — which emphasizes the tiling by triangles and the symmetries — and Klein's quartic equation, which shows how to get everything starting from the equation \[ u^3 v + v^3 w + w^3 u = 0 \] Don't forget Silvio Levy's online book. If you're interested in Felix Klein and his "Erlangen Program", you might also take a look at "week213".
Text © 2013 John Baez
Images copyrighted by those who made them.
baez@math.removethis.ucr.andthis.edu