




|
 
|

|
What common English slang phrase alludes to the number 168?
I won't tell you - not right away. But, I'll tell you a bunch of other cool stuff about this number, and eventually the answer should jump out at you.
Okay:
Start with a bunch of equilateral triangles. Glue them together so that 3 meet at each corner. You get a regular tetrahedron.
Next, take a bunch of squares. Glue them together so that 3 meet at each corner. You get a cube.
Next, take a bunch of regular pentagons. Glue them together so that three meet at each corner. You get a regular dodecahedron.
This is fun! We're getting a series of Platonic solids.
Next, take a bunch of regular hexagons and glue them together so that three meet at each corner. Now the angles of the hexagons add up to 360 degrees, so we don't get a Platonic solid. Instead, we get a tiling of the plane. It looks like a honeycomb that stretches out forever in all directions.
But, if you want something finite in size, you can cut out a portion of this honeycomb and curl it up to get a doughnut, or torus. There are actually lots of ways to do this. You might have fun figuring out what they all are. Can you take just one regular hexagon and curl it up to form a torus?
Anyway, these tori deserve to be called "Platonic surfaces", since they are surfaces tiled with regular polygons, with the same number meeting at each vertex.
Next, let's take a bunch of regular heptagons and glue them together so that three meet each corner. Now the angles add up to more than 360 degrees, so we get a tiling of the "hyperbolic plane". The hyperbolic plane is like the opposite of a sphere, since it's saddle-shaped at every point instead of bulging out at every point. In fact the sphere and the hyperbolic plane are the two most symmetrical forms of non-Euclidean geometry. The sphere is "positively curved", while the hyperbolic plane is "negatively curved".
You may have trouble visualizing the hyperbolic plane tiled with regular heptagons, but if we distort it, it fits into a disk and looks really pretty! Here it is:
1) Don Hatch, Hyperbolic planar tesselations, http://www.hadron.org/~hatch/HyperbolicTesselations/
It's called "{7,3}", since it's made of 7-sided figures with 3 meeting at each corner.
In this picture there's one heptagon at the center, surrounded by rings of heptagons that appear smaller (but aren't really - that's just an effect of the distortion).
Can we cut out a portion of this tiling and curl it up to get a torus? No! But, we can curl up a portion to get a 3-holed torus - like the surface of a doughnut with three holes. But, we can only do this if we use precisely 24 heptagons!
Here's how we do it. Here's a picture of 24 heptagons, taken from an old paper by Klein and Fricke but prettied up a bit:
2) Tony Smith, Klein's quartic surface, http://www.valdostamuseum.org/hamsmith/cdomain.html#tesselations
You'll notice they're drawn in a fancy style: each heptagon has been "barycentrically subdivided" into 14 right triangles. But don't worry about that yet; concentrate on the heptagons.
There's a blue heptagon in the middle, 7 red ones touching that, 7 yellow ones touching those, then 7 green ones falling off the edge of the picture, and 2 blue ones broken into bits all around the corners of the picture. That's a total of 24 heptagons.
We wrap this thing up into a 3-holed torus using the numbers on the edges of the picture:
In other words, connect edges 2n+1 and 2n+6 mod 14. To connect them the right way, make sure that triangles of the same color never touch each other.
Here's how to see if you get the idea. Ignore the little triangles; just pay attention to the heptagons! Then:
Start on any edge of any heptagon and march along in either direction.
Then, when you get to the end, turn left.
Then, when you get to the end, turn right.
Then, when you get to the end, turn left.
Then, when you get to the end, turn right.
Then, when you get to the end, turn left.
Then, when you get to the end, turn right.
Then, when you get to the end, turn left.
Then, when you get to the end, turn right.
You should now be back where you started!!!
These are like the driving directions the devil gives people who ask the way out of hell. LRLRLRLR and you're right back where you started.
But the resulting Platonic surface is heavenly. It has lots of symmetries. Each of the 24 heptagons has 7-fold rotational symmetry - and amazingly, all these rotations extend to a symmetry of the Platonic surface!
Now let's talk about those little triangles. Since our surface is made of 24 heptagons, each chopped into 14 right triangles, there are a total of
24 × 14 = 336
triangles. And this number is also the number of symmetries of the Klein quartic, including reflections!
This is no coincidence. We can specify a symmetry by saying where it sends our favorite right triangle. Since it can go to any other triangle, there are 336 possibilities. If we exclude reflections, we get half as many symmetries: 24 × 7 = 168.
By the way, this trick works for ordinary Platonic solids as well. For example, if we take a dodecahedron and barycentrically subdivide all 12 pentagons, we get 10 x 12 = 120 right triangles. If we pick one of these as the "identity element", we can specify any symmetry by saying which triangle this triangle gets sent to. So, the set of triangles becomes a vivid picture of the 120-element symmetry group of the dodecahedron. It's called the "Coxeter complex". This idea generalizes in many directions, and is incredibly useful.
Anyway... there is much more to say about this stuff. For example, if we take our hyperbolic plane tiled with heptagons and count them grouped according to how far they are from the central one, we get the sequence
7, 7, 14, 21, 35, 56, 91, ....
These are 7 times the Fibonacci numbers!
To dig a bit deeper, though, it helps to think about complex analysis.
If we think of the hyperbolic plane as the unit disc in the complex plane, this surface becomes a "Riemann surface", meaning that it gets equipped with a complex structure. This was Felix Klein's viewpoint when he discovered all this stuff in about 1878. He showed this surface could be described by an incredibly symmetrical quartic equation in 3 complex variables:
u3 v + v3 w + w3 u = 0
where we count two solutions as the same if they differ by an overall factor. So, it's called "Klein's quartic curve".
(Why a "curve" and not a surface? Because it takes one complex number to say where you are on it. We have 3 unknowns and one equation, but we mod out by an overall factor, so we get something locally parametrized by one complex number... so algebraic geometers call it a curve.)
You can read Klein's original article translated into English. It's available online as part of a whole book about his incredible quartic:
3) Silvio Levy, The Eightfold Way: the Beauty of Klein's Quartic Curve, MSRI Research Publications 35, Cambridge U. Press, Cambridge 1999. Also available as http://www.msri.org/publications/books/Book35/
This book was put out by the Mathematical Sciences Research Institute in Berkeley, to celebrate the completion of sculpture of Klein's quartic curve made by Helaman Ferguson. I must admit that the sculpture leaves me unmoved. But the curve itself - ah, that's another story!
For example, Klein's quartic curve turns out to have the maximum number of symmetries of any 3-holed Riemann surface.
Let's back up a minute and think about a Riemann surface with no holes: a sphere. There's only one way to make a sphere into a Riemann surface - it's called the Riemann sphere. You can think of it as the complex numbers plus a point at infinity. This has infinitely many symmetries. They're called conformal transformations, and they all look like this:
az + b
z |---> --------
cz + d
They form a group called PSL(2,C), since it's the same as the group of
2x2 complex matrices with determinant 1, mod scalars. It's also the
same as the Lorentz group!
There are different ways to make a torus into a Riemann surface, some with more symmetries than others (see "week124"). But, there are always translation symmetries in both directions, so the symmetry group is always infinite.
On the other hand, a Riemann surface with 2 or more holes can only have a finite group of conformal transformations. In fact, in 1893 Hurwitz proved that a Riemann surface with g holes has at most
84(g - 1)
For g = 3, this is 168. So, Klein's quartic surface is as symmetrical as possible! (We don't count reflections here, since they don't preserve the complex structure - they're like complex conjugation.)
Now I should break down and give the best description of Klein's quartic curve as a Riemann surface. Sitting inside PSL(2,C) is PSL(2,Z), where we only use integers a,b,c,d in our fractional linear transformation
az + b
z |---> --------
cz + d
This subgroup acts on the upper half-plane H, which is just another
way of thinking about the hyperbolic plane.
Sitting inside PSL(2,Z) is a group Γ(7) consisting of guys where the matrix
a b c dis congruent to the identity:
1 0 0 1modulo 7. This is an example of a "congruence subgroup"; these serve to relate complex analysis to number theory in lots of cool ways. In particular, Klein's quartic curve is just
H/Γ(7)
Since Γ(7) is a normal subgroup of PSL(2,Z), the quotient group
PSL(2,Z)/Γ(7) = PSL(2,Z/7)
acts as symmetries of Klein's quartic curve. And, this group has 168 elements!
In fact, this group is the second smallest nonabelian simple group. The smallest one is the rotational symmetry group of the icosahedron, which has 60 elements. This group is actually PSL(2,Z/5), and Klein had run into it in his work on the icosahedron and quintic equations (see "week213"). So, it's actually far from sheer luck that he then moved on to PSL(2,Z/7) and ran into his wonderful quartic curve.
By the way, this 168-element group is also known as PSL(3,Z/2) - the symmetry group of the "Fano plane". This is a name for the projective plane over Z/2. The Fano plane is closely related to the octonions:
3) John Baez, The Fano plane, http://math.ucr.edu/home/baez/octonions/node4.html
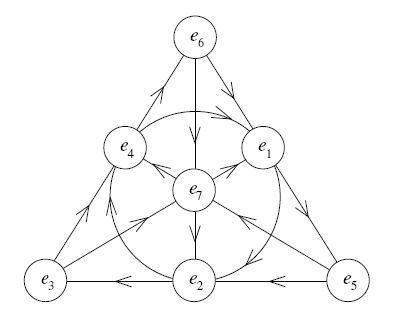
So in fact, our 168-element group acts on the set of octonion multiplication tables:
4) Tony Smith, Octonion products, http://www.valdostamuseum.org/hamsmith/480op.html
5) Geoffrey Dixon, Octonion multiplication tables, http://www.7stones.com/Homepage/octotut0.html
And, as James Dolan just noted today, and Tony Smith seems to have known all along, there's a way to draw the Fano plane that even looks like the diagram Klein and Fricke used to build the Klein quartic. Here's a picture drawn by Burkard Polster, author of "The Mathematics of Juggling" and "Geometries on Surfaces":
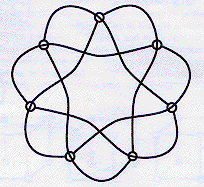
So, something interesting is going on, and I want to know what it is!
By the way, fans of the quaternions and octonions may like this review of Conway and Smith's book:
6) John Baez, review of "On Quaternions and Octonions: Their Geometry, Arithmetic and Symmetry", by John H. Conway and Derek A. Smith, Bull. Amer. Math. Soc. 42 (2005), 229-243. Available at http://www.ams.org/bull/2005-42-02/ and http://math.ucr.edu/home/baez/octonions/node24.html
It's packed with cool pictures and weird facts - a more refined version of the material in "week193" and "week194".
It builds up to a kind of crazy climax in which I describe how when you pack spheres as densely as possible in 8 dimensions, each sphere touches 240 others... and if you look at the 240 neighbors of a given sphere, each one of those neighbors touches 56 other neighbors. Then I explain how this gives rise to a 56-dimensional representation of the exceptional group E7 - its smallest nontrivial representation! And, how it gives rise to a 57-dimensional manifold on which the exceptional group E8 acts - the smallest space on which it acts nontrivially!
Bertram Kostant is one of the real gurus of Lie theory. He teaches at MIT, and he has a strong fondness for exceptional Lie groups. When he saw this review of mine, he mentioned a couple of other papers that construct the 57-dimensional space on which E8 acts:
7) Ranee Brylinski and Bertram Kostant, Lagrangian models of minimal representations of E6, E7, and E8, in Functional Analysis on the Eve of the 21st Century, vol. 1, Progress in Math. 131, Birkhauser, Boston, 1995, pp. 13-53.
Bertram Kostant, Minimal coadjoint orbits and symplectic induction, in The Breadth of Symplectic and Poisson geometry, 391-422, Progress in Math. 232, Birkhauser, Boston, 2005. Also available as http://www.arXiv.org/abs/math.SG/0312252
I've got to read these sometime.
Having the number 56 on my brain, I can't resist nothing that if you take Klein's quartic curve tiled by heptagons, and you count the vertices, you get
24 × 7 / 3 = 56
since each vertex is shared by 3 heptagons. I'm hoping this is not a coincidence!
Okay, that's all for this week, except for some silly stuff....
First of all, speaking of octonions, Geoff Corbishley just told me that their inventor, John Thomas Graves, is a relative of Robert Graves - the author of "I Claudius".
Second of all, I hope you've figured out the puzzle I gave at the beginning of this Week. The phrase is "24-7", as in "we're working on it 24-7". 24 hours a day, 7 days a week, makes 168 hours per week!
Finally, speaking of numerology, this number 168 is related to why the days of the week have the names they do! I explained why in "week175", but I'll remind you:
Astrologers liked to list the planets in order of decreasing orbital period, counting the sun as having a period of one year, and the moon as period of one month:
Saturn (29 years) Jupiter (12 years) Mars (687 days) Sun (365 days) Venus (224 days) Mercury (88 days) Moon (29.5 days)For the purposes of astrology they wanted to assign a planet to each hour of each day of the week. To do this, they assigned Saturn to the first hour of the first day, Jupiter to the second hour of the first day, and so on, cycling through the list of planets over and over, until each of the 24 × 7 = 168 hours was assigned a planet. Each day was then named after the first hour in that day. Since 24 mod 7 equals 3, this amounts to taking the above list and cycling around it, reading off every third planet:
Saturn (Saturday) Sun (Sunday) Moon (Monday) Mars (Tuesday) Mercury (Wednesday) Jupiter (Thursday) Venus (Friday)And that's how they got listed in this order! At least, this is what the Roman historian Dion Cassius (AD 150-235) claims. Nobody knows for sure.
Addendum: Mike Stay took Don Hatch's picture and drew numbers from 1 to 24 showing how to identify heptagons in order to get the Klein quartic curve:

Gerard Westendorp had some interesting comments on what I wrote:
If you take Euler's formulaI replied:V+F-E = 2-2×holesthen you can figure out that for a (7,3) tiling with N heptagons, you haveV = 7N/3 F = N E = 7N/2so thatN = 12×(holes-1)Here's the table of solutions:holes N 0 -12 1 0 2 12 3 24 4 36 . . . .So indeed, there are no solutions for 0 holes (sphere) or 1 hole (torus). But a 2-holed torus should be possible, as well as the 24-faced 3-holed one.Anyway, see if I can visualise the 3-holed one.
If you start with a sphere, i.e. genus 0, and drill a tunnel through it, you will get a genus 1 object. On the outer surface, you see 2 holes, one for each side of the "tunnel". (I use the word "tunnel" for something into a 3D object, and "hole" for something in a 2D surface.)
Next, you can drill a second tunnel, and get a genus 2 object, and you would see 4 holes on the outer surface. But a nice trick is to drill not to the outer surface, but to a secret "cave" in the middle where you meet the first tunnel. Here you stop drilling. To complete the genus-3 object, you drill the third tunnel again not to the outer surface, but to the central cave. Thus, you get and object with genus 3, which has 4 holes on its outer surface, each leading to a central cave.
Confusingly, 4 tunnels to a central cave is topologically the same as 3 separate tunnels! The trick is that tunnels do not have to end on the outer surface, the inner surface is topologically the same.
OK, so we have an object with 4 holes on its outer surface. 4 holes → tetrahedron...
I built a cardboard model of a tetrahedron with a central cave. Truncated tetrahedrons together with tetrahedrons can fill space. So you can stack 4 truncated tetrahedra on top of each other, leaving a hole in the shape of an imaginary 5th one. Then use tetrahedra to fill up some gaps. This was basically the shape I built outof cardboard. Then, I spent rather a long time trying to tile this with heptagons. A clue to a solution was that a triangulation of the surface I made had 120 triangle, and 120 = 24×5. What is so good about 5? Well, 5 triangles stuck together have 7 outer sides, sop they are a kind of pseudo heptagons. Anyway, I got a bit frustrated, and did not find a nice tiling.
As I was trying to figure it out, I found this site:
http://www.math.uni-siegen.de/wills/klein/
It has some nice pictures.
> These are like the driving directions the devil gives people who ask > the way out of hell. LRLRLRLR and you're right back where you started.Btw, this works the same on other polyhedra, e.g. the cube.> Saturn (Saturday) > Sun (Sunday) > Moon (Monday) > Mars (Tuesday) > Mercury (Wednesday) > Jupiter (Thursday) > Venus (Friday)My French is not so good, but in French some names look more convincing:tuesday = mardi (Mars?) wednesday = mercredi (Mercury?) thursday = jeudi (Jove?) friday = vendredi (Venus?)Gerard
Gerard Westendorp wrote:> John Baez wrote: > > It's called "{7,3}", since it's made of 7-sided figures with 3 > > meeting at each corner. > > Can we cut out a portion of this tiling and curl it up to get > > a torus? No! But, we can curl up a portion to get a 3-holed > > torus - like the surface of a doughnut with three holes. But, > > we can only do this if we use precisely 24 heptagons! >If you take Euler's formula [....] >So indeed, there are no solutions for 0 holes (sphere), >1 hole( torus). But a 2-holed torus should be possible, >as well as the 24-faced 3-holed one.I was going to talk about this, but I figured my article was getting too long.Indeed, Euler's formula also allows the possibility of a 2-holed torus tiled with 12 heptagons meeting 3 at each corner.
But this does not prove such a tiling is possible. I don't know if it is! Someone should try it.
However: even if such a tiling exists, it's not possible for each rotational symmetry of each heptagon to extend to a symmetry of the whole tiled surface. What's marvelous about the 3-holed case is that they all do - at least if you do things correctly. This is what makes the Klein quartic a full-fledged "Platonic surface".
If you look here:
you'll see that Karcher and Weber study Platonic surfaces using Euler's formula.
- Hermann Karcher and Mattias Weber, The Geometry of Klein's Riemann Surface, in The Eightfold Way: the Beauty of Klein's Quartic Curve, ed. Silvio Levy, MSRI Research Publications 35, Cambridge U. Press, Cambridge 1999. Also available as PDF and gzipped Postscript.
On pages 13-19 they consider Platonic surfaces with 2 holes. On page 19 they give a clever proof that no tiling of the 2-holed torus by heptagons meeting 3 at each corner can be a Platonic surface. The proof is so clever that I don't understand it.
(Warning: their article starts on page 9.)
>Anyway, see if I can visualise the 3-holed one.I wish I could visualize it myself.>As I was trying to figure it out, I found this site: >http://www.math.uni-siegen.de/wills/klein/ >It has some nice pictures.These pictures are interesting, but what I'd really like is a nice picture of a 3-holed torus, not weird or crumpled up, which is tiled by 24 heptagons just like the Klein quartic.The heptagons can't all be regular if the torus is embedded in R3, since there's no way to embed a compact surface of constant negative curvature in R3. But, you can get the topology correct and still have the torus embedded in R3.
If anyone draws such a picture, and I think it looks nice, I'd love to put it on This Week's Finds!
If anyone wants instructions on how such a surface should be made, look above, where Mike Stay has kindly drawn numbers from 1-24 on a portion of the hyperbolic plane tiled with heptagons. These numbers indicate how to identify heptagons to get the Klein quartic. For example, all the heptagons labelled "21" are really the same heptagon in the Klein quartic.
> > Saturn (Saturday) > > Sun (Sunday) > > Moon (Monday) > > Mars (Tuesday) > > Mercury (Wednesday) > > Jupiter (Thursday) > > Venus (Friday) >My French is not so good, but in French some names look more >convincing: > > tuesday = mardi (Mars?) > wednesday = mercredi (Mercury?) > thursday = jeudi (Jove?) > friday = vendredi (Venus?)Yes, this because most of the English names for planets come from Latin, and French is more like Latin.English is more complicated, but I'm so used to it that I forgot people might find the connection to Latin mysterious:
- "Tuesday" comes from "Tiu" or "Tyr", an ancient Germanic god of war whom the Romans identified with Mars. We see traces of this in the German "Dienstag" as well.
- "Wednesday" comes from "Woden" or "Odin", a Germanic god whom the Romans identified with Mercury. Modern German uses "Mittwoch" instead, which means "mid-week".
- "Thursday" comes from "Thor", a Germanic thunder god whom the Romans identified with Jupiter. Modern German uses "Donnerstag" instead, with "Donner" meaning "thunder".
- "Friday" comes from "Freya" or "Frigga", a Germanic goddess of married love whom the Romans identified with Venus. The German "Freitag" is very similar.
© 2005 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|