The Yang-Baxter Equation

I find that Polyakov model I described last time to be a great example of all sort of things: solitons, instantons, anyons, nonlinear sigma models, gauge theories, and topological quantum field theories all in one! But I want to get back to braids plain and simple and introduce the Yang-Baxter equations. I'll tone down the math for a while so that people who know only a tad of group theory can at least get the definition of the braid group.

So: braids with $n$ strands form a group, called the braid group $B_n$. (Let's take $n = 4$ as an example.) Multiplication is just defined by gluing one braid onto the bottom of another. For example this braid:

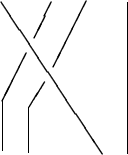
times this one:

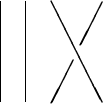
equals this:

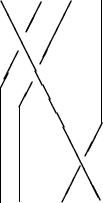
The identity braid is the most boring one:

I leave it as a mild exercise to show that every braid $x$ has an "inverse" $y$ such that $xy = yx = 1$.

The braid group has special elements $s_1,s_2,\ldots,s_{n-1}$, where $s_i$ is the braid where the $i$-th strand goes over and to the right of the $(i+1)$-st. For example, $s_2$ equals

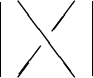
Now, the interesting thing about these "elementary braids" is that $s_i$ and $s_j$ commute if $\vert i - j\vert > 1$ (check it!) but $s_i$ and $s_{i+1}$ get tangled up in each other. They satisfy a simple equation, however, the Yang-Baxter equation. (This was known ages before Yang and Baxter came along, and its importance was perhaps discovered by Artin.) Namely,

$$s_i s_{i+1} s_i = s_{i+1} s_i s_{i+1}$$

Let me draw it for the braid group on three strands, where $i = 1$:

Draw it for yourself and check that these are topologically equivalent braids (i.e., you can get from one to the other by a little stretching and bending).

Okay, now I'll start turning the math level back up. The braid group is obviously generated by the elementary braids $s_i$, but the extremely non-obvious fact is that the braid group is isomorphic to the group with the $s_i$ as generators and the relations

$$\begin{array}{ll} s_i s_j = s_j s_i & {\rm for } \vert i-j\vert > 1\\ s_i s_{i+1} s_i = s_{i+1} s_i s_{i+1}\\ \end{array}$$

Note that there's a homomorphism from the braid group onto the symmetric group with $s_i$ mapped to the ith elementary transposition. In fact the symmetric group may be obtained by throwing in the relations

$$s_i s_i = 1$$

in with the above ones. In other words -- and this has a lot of physical/philosophical significance -- the braid group may be thought of as the obvious generalization of the group of permutations to a situation in which "switching" two things' places twice does not get you back to the original situation. In physics, of course, this happens with anyons.

It's easy to determine the one-dimensional unitary representations of the braid group. In such a representation each $s_i$ gets mapped to a complex number of unit magnitude, which we'll just call $s_i$. Then the Yang-Baxter equation shows that $s_i = s_{i+1}$, so all the $s_i$'s are equal. The other braid group relations are automatic. Thus for each angle $\theta$ there is a unitary rep of the braid group with

$$s_i \rightarrow e^{i \theta}$$

and these are all the one-dimensional unitary reps. In physics lingo these are all "fractional statistics." Note that for one of these reps to quotient through the symmetric group we must have $e^{i \theta}=\pm 1$; these correspond to bosonic and fermionic statistics respectively.

Okay, how about reps of the braid group that are not necessarily one-dimensional? Well, suppose $V$ is a vector space and we want to get a rep of $B_n$ on the $n$-th tensor power of $V$, which I'll call $V^n$. Here's a simple way: just map the $i$-th elementary braid $s_i$ to the linear map taking

$$v_1\otimes v_2\otimes ...\otimes v_n$$

to

$$v_1\otimes\ldots\otimes R(v_i\otimes v_{i+1})\otimes \ldots\otimes v_n$$

where $R$ is an invertible linear transformation of $V^2$. In other words, we use $R$ to "switch" the $i$-th and $(i+1)$-st factors, and leave the rest alone. It's easy to see that this defines a rep of the braid group as long as we can get the Yang-Baxter equation to hold, and this is equivalent to having

$$(R\otimes I)(I\otimes R)(R\otimes I) = (I\otimes R)(R\otimes I)(I\otimes R)$$

where $I$ is the identity on $V$. Actually, this equation is more usually known as the Yang-Baxter equation.

Now, Baxter invented this equation when he was looking for problems in 2d statistical mechanics that were exactly solvable (i.e. one could calculate the partition function). A simple example is the "six-vertex" or "ice-type" model, so-called because it describes flat square ice! (Theoretical physicists are never afraid of simplifying the world down to the point where they can understand it.) But there are zillions of examples -- take a look at his book on exactly solvable statistical mechanics models! Similarly, Yang ran into the equation while trying to cook up 2d quantum field theories for which one could exactly calculate the S-matrix. I won't get into how this equation does the trick right now; I just want to note that a whole industry developed of finding solutions to the Yang-Baxter equations. This eventually led to the discovery of quantum groups...but for now I'll leave you with a nice solution of the Yang-Baxter equations: let $V$ be spanned by two vectors $X$ and $Y$, and define $R$ by

$$\begin{eqnarray*} R(X\otimes X) &=& X\otimes X \\ R(Y\otimes Y) &=& Y\otimes Y ... ...X)\\ R(Y\otimes X) &=& q(X\otimes Y) + (1 - q^2)(Y\otimes X)\\ \end{eqnarray*}$$

Exercise: check that $R$ satisfies the Yang-Baxter equations and $R^2 = (1 - q^2)R + q^2$. This quadratic equation is called a Hecke relation.

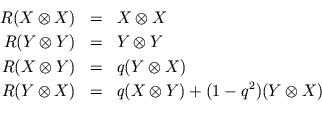
If you are interested in learning about quantum groups, the Yang-Baxter equations, and braids, I suggest taking a look at the following books:

• L. Kauffman, Knots and Physics, World Scientific, New Jersey, 1991.

• C. Yang and M. Ge, Braid Group, Knot Theory, and Statistical Mechanics, World Scientific, New Jersey, 1989.

• T. Kohno, New Developments in the Theory of Knots, World Scientific, New Jersey, 1990.

• Yu. I. Manin, Quantum Groups and Noncommutative Geometry, Les Publ. du Centre de Récherches Math., Universite de Montreal, Montreal, 1988.

© 1992 John Baez
baez@math.removethis.ucr.andthis.edu

home