
Today Lisa and I explored Prambanan, the largest Hindu temple in Java. I was overwhelmed by the massive structures - at the bottom you'll see tiny people.
How was it built? It all started when a prince named Bandung Bondowoso fell in love with a beautiful princess named Rara Jonggrang. He proposed marriage. She rejected him because he had killed her father, the cruel man-eating giant King Boko. But Bandung Bondowoso insisted. Finally Rara Jonggrang relented and agreed to marry him... but only on one condition: he had to build her a thousand temples in one night.
The Prince entered into meditation and conjured up a multitude of demons from the earth. With their help, he succeeded in building 999 temples. But just as he was about to complete his task, the princess woke her palace maids and ordered the women of the village to begin pounding rice and set a fire in the east of the temple, to make the prince and his demons believe that the sun was about to rise.
As the cocks began to crow, fooled by the light and the typical sounds of morning, the prince's demon helpers fled back into the ground. The prince was furious! In revenge he cursed Rara Jonggrang — and turned her to stone. She became the last and most beautiful of the thousand temples.
Well, okay — this is how the local Javanese peasants _said_ these temples were built, long after they were actually built in 850 AD, abandoned to the jungle after a volcanic eruption in 930, and partially destroyed by a major earthquake in the 1600s. In reality they were built by the Medang Kingdom, a Hindu-Buddhist kingdom that thrived from 732 to 1006 AD, whose sphere of influence reached all the way to Angkor Wat in Cambodia.
Speaking of "demons from the earth": in California we have earthquakes, but in Java you _really_ sense the power of shifting tectonic plates! As recently as February last year, Borobudur and Prambanan were closed due to volcanic ashes from the eruption of a volcano called Raung 200 kilometers away. Four years earlier, a much closer volcano called Merapi erupted. You can see this one towering over Yogyakarta on days when the clouds and smog aren't too thick. But the ashes from that eruption missed Prambanan, and only hit Borobudur. Right now yet another volcano on Java, Raung, is disrupting air travel to Bali.
Today Lisa and I visited Borobudur, the largest temple in Java, and the biggest Buddhist temple in the world.
Nobody knows who built it, sometime around 800 AD. It was eventually abandoned, and it lay hidden for centuries, gradually buried by volcanic ash and thick jungle growth. In 1814, the British colonist Thomas Raffles — who also founded Singapore — traveled through Java and heard of a huge monument near Yogyakarta, the old capital of this island. He got a Dutch engineer to investigate, and by 1885 the jungle was cleared away and the full extent of Borobudur was revealed!
The picture above is from Trey Ratcliff. It shows the view from the top of Borobudur, which is covered with giant bell-like stupas.
Built of 2 million stone blocks, Borobudur is actually designed in the form of a mandala: a diagram of Buddhist cosmology that serves as an aid to meditation. From above, it looks like this:
At the bottom is the outer square wall. Then there are 5 nested square levels, each a bit smaller than the one below, connected by stairs. Then there are 3 round levels. The first has 32 bell-like stupas on it, the second has 24, and the third has 16. Finally, there is a huge central stupa at the very top.
The bottom level of Borobodur represents Kāmadhātu: the world of desires. The ideas is that most sentient beings live here.
The 5 square levels represent Rūpadhātu: the world of forms, or patterns. Beings who have burnt out their desire for continued existence live here: they see forms, but aren't drawn to them.
The 3 round levels on top represent Arūpadhātu, the formless world. The idea is that buddhas live here: they go beyond form and experience reality at its most fundamental level, the formless ocean of nirvana.
Here is a cross-section:
The idea is that pilgrims should go up one level at a time, walking all the way around and meditating on the wall carvings and statues before climbing the steep stairs to the next level. The pilgrim's walk to the top is 5 kilometers long, and it passes by 1460 stone panels illustrating stories, as well as 1212 decorated panels.
Here's Lisa walking along one of the lower terraces of Borobudur, looking at these panels. She's somewhere in Rūpadhātu, the world of forms:
As we remember the bombing of Hiroshima 70 years ago today, let's not forget that the US strategy of mass slaughter of Japanese civilians didn't start there. 70 years ago on March 10th, even more people were killed in the firebombing of Tokyo — a city where most houses were made of paper.
279 planes flew over the city and dropped 1,665 tons of bombs. Most were 500-pound cluster bombs, each one releasing 38 incendiary bomblets at an altitude of about 2000 feet. These bomblets punched through the roofs of people's houses or landed on the ground and ignited 3.5 seconds later, throwing out jets of flaming, sticky napalm.
The planes also dropped 100-pound jelled-gasoline and white phosphorus bombs that ignited upon impact. The city's fire departments were overwhelmed, and the individual fires started by the bombs joined to create a huge conflagration that destroyed 16 square miles of the city. Over 100,000 people died — nobody knows how many, and both the Japanese and Americans had reasons to underestimate the casualties.
General Curtis LeMay, who led this attack, said:
Killing Japanese didn't bother me very much at that time... I suppose if I had lost the war, I would have been tried as a war criminal.
Joe O'Donnell, a marine sent in after the war to document the effects of the bombing, wrote:
The people I met, the suffering I witnessed, and the scenes of incredible devastation taken by my camera caused me to question every belief I had previously held about my so-called enemies.
The picture above shows the charred corpse of a woman in Tokyo who was carrying a child on her back. In this style of war, cities of people, many perfectly innocent, are treated like rats to be exterminated. Martin Middlebrook captured the horror of this in Hamburg, one of the German cities firebombed by the US:
A thermal column of wind generated heat in excess of 1,400 degrees Fahrenheit, melting trolley windows and the asphalt in streets, the wind uprooting trees. When people crossed a street, their feet stuck in the melted asphalt; they tried to extricate themselves with their hands, only to find them stuck as well. They remained on all fours screaming. Small children lay like "fried eels" on the pavement. The firestorm sucked all the oxygen out of the city.Let's try to avoid this, eh? It's not necessarily easy, and I'm not saying I know how, but let's try to avoid making our world into a hell.
(Over
on Google+, we had a conversation about how.)
August 12, 2015
Here you can see a plane moving though a cone. Most of the time the plane intersects the cone in a curve. These curves are called 'conic sections'. They have famous names and formulas:
I haven't given the most general formula for each kind of curve, but my formulas are enough to describe all possible shapes and sizes of these curves. For example, if you have an upside-down parabola \(y = -2x^2\) you can rotate it so it looks like \(y = x^2\). So, I say they have the same shape, and I don't bother listing both.
However, there are a few other cases that aren't on this list, which are still extremely important! These are the other shapes you can define using equations of the form $$ ax^2 + bxy + cy^2 = 0 $$
Ordinary folks wouldn't call these 'curves'. The last two special cases are especially upsetting! But the famous mathematician Grothendieck figured out a way to improve algebraic geometry so that these cases are on the same footing as the rest. In particular, he made it really precise how $$ x^2 = 0 $$ is different, in an important way, from $$ x = 0 $$ The second one is an ordinary line, given by a linear equation. The first one is a 'double line', the limit of two lines as they get closer and closer! Watch the movie and see how we get to this 'double line', and you'll see what I mean.
People in algebraic geometry had already thought about 'double lines' and similar things, but Grothendieck's theory of 'schemes' explained what these things really are. Whatever it is, a double line is not just set of points in the plane — if we look at the set of points, there's no difference between the double line $$ x^2 = 0 $$ and the single line $$ x = 0 $$
The double line is something else — it's a 'scheme'.
But now it's time for breakfast, so I can't tell you what a 'scheme' actually is. Instead, I'll just say this. Any set of polynomial equations defines an 'affine scheme', and that's not a very complicated thing. Alexander Grothendieck's real stroke of genius was to develop a more general notion of scheme, which is built out of pieces that are affine schemes. Grothendieck developed schemes, and more, as part of his attack on a very hard problem in number theory, called the Weil conjectures. But his attack was a gentle one. Instead of using brute force to crack this nut, he preferred to slowly 'soften' the problem by inventing new concepts. Here's what he wrote about this:
The analogy that came to my mind is of immersing the nut in some softening liquid, and why not simply water? From time to time you rub so the liquid penetrates better, and otherwise you let time pass. The shell becomes more flexible through weeks and months — when the time is ripe, hand pressure is enough, the shell opens like a perfectly ripened avocado!The gif in this post is from Math Gif.
Newton said he saw further because he stood on the shoulders of giants. But this amazing sculpture illustrates how we're also weighed down and blinded by the prejudices of those who came before us — who were in turn blinded by their predecessors.
This sculpture is called 'Karma'. It was made by the Korean artist Do Ho Suh. It looks infinitely tall, especially in the first picture above. But in fact it's 7 meters tall (23 feet), built from 98 figures of men, each one covering the eyes of the one below. I think it looks taller because they shrink as you go further up, providing a false perspective that makes them seem to go on forever. You can see more photos here:
The photos were taken by by Lehmann Maupin, Alan Teo and Eric Harvey Brown, and CamWall.
This sculpture can be seen at the Sydney and Walda Besthoff Sculpture Garden at the New Orleans Museum of Art, so if you're anywhere near New Orleans, check it out!
As I mentioned, Newton said:
If I have seen further, it is by standing on the shoulders of giants.
He said this in response to a letter to his competitor Robert Hooke, and some have interpreted it as a sarcastic poke at Hooke's slight build. But in fact they were on good terms at the time, and came to dislike each other only later.
Murray Gell-Mann, the theoretical physicist who came up with the idea of 'quarks', was definitely taking a poke at his competitors when he said:
If I have seen further, it is because I was surrounded by dwarves.
Ouch! Over on G+, Esko Arajärvi provided some other versions:
In the sciences we are now uniquely privileged to sit side by side with the giants on whose shoulders we stand. — Gerald Holton
If I have not seen as far as others, it is because giants were standing on my shoulders. — Hal AbelsonFor more on the history of such quotes, see:
Brian Koberlein, one of the most consistently energetic and interesting people on Google+, recently wrote about how to make a black hole.
His recipe works like this:
INGREDIENTS: one small neutron star, one solar mass of hydrogen.Take a neutron star 2 weighing solar masses. Gradually add one solar mass of hydrogen gas, letting it fall to the surface of the neutron star. Be careful: if you add too much too quickly, you'll create a huge nuclear explosion called a nova. When your neutron star reaches 3 solar masses, it will collapse into a black hole.
This is the smallest type of black hole we see in nature. The problem with this recipe is that we'd need to become at least a Kardashev Type II civilization, able to harness the power of an entire star, before we could carry it out.
My friend Louis Crane, a mathematician at the University of Kansas, has studied other ways to make a black hole. It's slightly easier to make a smaller black hole — and perhaps more useful, since the Hawking radiation from a small black hole could be a good source of power.
Crane is interested in powering starships, but we could also use this power for anything else. It's the ultimate power source: you drop matter into your black hole, and it gets turned into electromagnetic radiation!
Unfortunately, even smaller black holes are tough to make. Say you want to make a black hole whose mass equals that of the Earth. Then you need to crush the Earth down to the size of a marble. The final stage of this crushing process would probably take care of itself: gravity would do the job! But crushing a planet to half its original size is not easy. I have no idea how to do it.
Luckily, to make power with Hawking radiation, it's best to make a much smaller black hole. The smaller a black hole is, the more Hawking radiation it emits. Louis Crane recommends making a black hole whose mass is a million tonnes. This would put out 60,000 terawatts of Hawking radiation. Right now human civilization uses only 20 terawatts of power. So this is a healthy power source.
You have to be careful: the radiation emitted by such a black hole is incredibly intense. And you have to keep feeding it. You see, the smaller a black hole is, the more Hawking radiation it emits — and as it emits radiation, it shrinks! Eventually it explodes in a blaze of glory: in the final second, it's about 1/100 as bright as the Sun. To keep your black hole from exploding, you need to keep feeding it. But for a black hole a million tons in mass, you don't need to rush: it will last about a century before it explodes if you don't feed it.
Unfortunately, to make a black hole that weighs a million tonnes, you need to put a million tonnes of mass in a region 1/1000 times the diameter of a proton.
This is about the wavelength of a gamma ray. So, if we could make gamma ray lasers, and focus them well enough, we could in theory put enough energy in a small enough region to create a million-ton black hole. He says:
Since a nuclear laser can convert on the order of 1/1000 of its rest mass to radiation, we would need a lasing mass of about a gigatonne to produce the pulse. This should correspond to a mass of order 10 gigatonnes for the whole structure (the size of a small asteroid). Such a structure would be assembled in space near the sun by an army of robots and built out of space-based materials. It is not larger than some structures human beings have already built. The precision required to focus the collapsing electromagnetic wave would be of an order already possible using interferometric methods, but on a truly massive scale. This is clearly extremely ambitious, but we do not see it as impossible.
I'm not holding my breath, but with luck our civilization will last long enough, and do well enough, to try this someday.
For details, see:
It's a bit surprising. You can take 8 perfectly rigid regular tetrahedra and connect them along their edges to form a ring that you can turn inside-out!
It's called a 'kaleidocycle', and you can actually make one with any even number of tetrahedra, as long as you have at least 8. Fewer than 8, and they bump into each other.
You can see kaleidocycles with 8, 10, and 12 tetrahedra here:
You can also make kaleidocycles out of paper:
What's all this good for? I have no idea. But it illustrates the limits of the Rigidity Theorem. This theorem says if the faces of a convex polyhedron are made of a rigid material and the polyhedron edges are hinges, the polyhedron can't change shape at all: it's rigid. The kaleidohedra show this isn't true for a polyhedron with a hole in it.
Of course, having a hole is an extreme case of being nonconvex. To be nonconvex, your polyhedron only needs to have a 'dent' in it. And there are nonconvex polyhedra without a hole that aren't rigid! The first of these was discovered by a guy named Connelly in 1978. It has 18 triangular faces.
In 1997, Connelly, Sabitov and Waltz proved something really cool: the Bellows Conjecture. This says that a polyhedron that's not rigid must keep the same volume as you flex it!
The famous mathematician Cauchy claimed to prove the Rigidity Theorem in 1813. But there was a mistake in his proof. Nobody noticed it for a long time. It seems mathematician named Steinitz spotted the mistake and fixed it in a 1928 paper.
Puzzle 1: what was the mistake?
Still, people often call this result 'Cauchy's Theorem', which is really unfair, especially since Cauchy has other, better, theorems named after him.
Later the rigidity theorem was generalized to higher-dimensional convex polytopes. (A polytope is a higher-dimensional version of a polyhedron, like a hypercube.)
It's also been shown that 'generically' polyhedra are rigid, even if they're not convex. In other words: if you take one that's not rigid, you can change its shape just a tiny bit and get one that's rigid.
So, there are lots of variations on this theme: it's very flexible.
Puzzle 2: can you make higher-dimensional kaleidocycles out of higher-dimensional regular polytopes? For example, a regular 5-simplex has 6 corners; if you attach 3 corners of one to 3 corners of another, and so on, maybe you can make a flexible ring. Unfortunately this is in 5 dimensions — a 4-simplex has 5 corners, which doesn't sound so good, unless you leave one corner hanging free, in which case you can just take the movie here and imagine it as the 'bottom' of a 4d movie where each tetrahedron is the 'base' of a 4-simplex: sort of boring.
Puzzle 3: is a version of the Bellows Conjecture true in higher dimensions?
For more, check out these:
For some answers and discussions, see my G+ post.
August 19, 2015
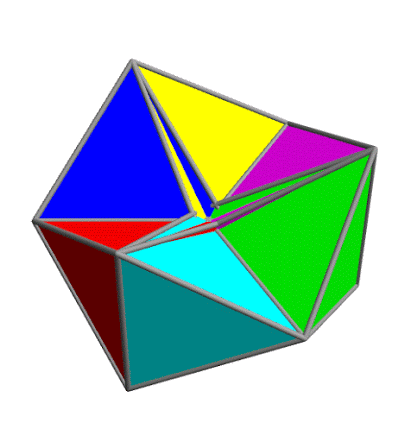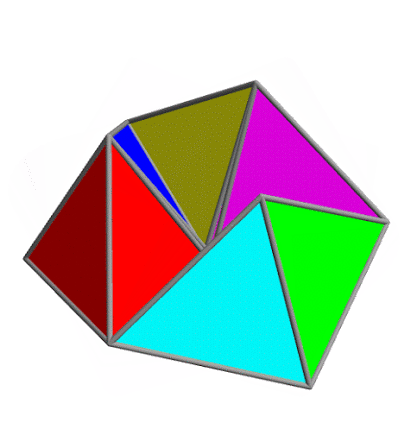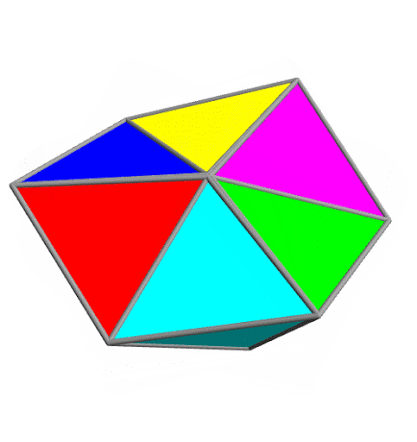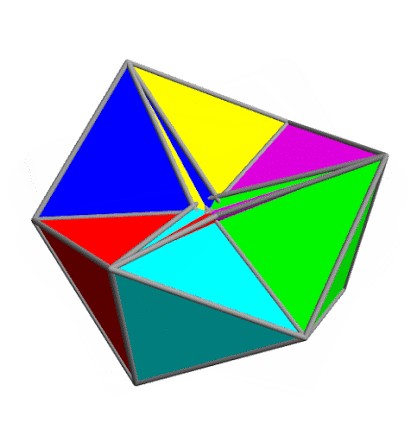
My last entry showed a 'kaleidocycle' — a ring of 8 regular tetrahedra joined edge to edge, that you could turn inside out. I said you could build one with any even number of tetrahedra that's at least 8.
Then somebody told me he'd built one with just 6.
Here is Greg Egan's movie of what happens if you try a kaleidocycle with 6 regular tetrahedra. They collide! Very slightly. So, it's not a true kaleidocyle: it's a 'collidocyle'.
In other words: if these tetrahedra are completely rigid, they must pass through each other as they turn. But if you made one out of paper, you might be able to force it to work, by bending the paper slightly.
Puzzle 1: Give a mathematical proof that the tetrahedra here must intersect at some point, if they're completely rigid.
Puzzle 2: What's the maximum fraction of the volume here that's contained in the intersection of at least two tetrahedra? It looks like about 2% to me.
Greg Egan made his gif by adapting the Mathematica code at the website I showed you before:
Prometheus and Pandora were characters in a Greek myth, but now they are moons of Saturn. They both orbit close to Saturn's F ring, zipping around this planet once every 15 hours or so.
Here you can see Prometheus carving strange slots in the F ring:

This ring is made of ice boulders, maybe up to 3 meters across. Sometimes these chunks of ice form temporary clumps up to 10 kilometers in size. At other times, these clumps get pulled apart. Prometheus steals boulders from the F ring with its gravitational pull. And each time it comes as close as possible to Saturn, it carves a new slot in the F ring.
Why does this happen? It's complicated, and people keep learning more about it. I'm certainly no expert!
People used to call Prometheus and Pandora shepherd moons. The idea was that they help stabilize the F ring. It's an attractive notion. The singer Enya even made an album with this title.
But more recent work casts doubt on this theory. Last month Emily Lakdawalla of the Planetary Society wrote:
The most surprising thing I've learned: You know how Prometheus and Pandora are the F ring shepherds? Prometheus on the inside, and Pandora on the outside, herding the billions of tiny particles that make up the ring into place? It's not true. Pandora is not involved in controlling the F ring's tight shape.According to her account of some recent papers, the key is a kind of resonance. Resonant frequencies shape Saturn's rings in many ways, but here the key is something called a 'Lindblad resonance'.The first paper I looked at was written by Jeff Cuzzi and seven coauthors: "Saturn's F Ring core: Calm in the midst of chaos." (Let's pause for a moment to appreciate the quality of that paper title, which is both interesting and accurate, not boring or silly.) The paper seeks to explain why the central core of Saturn's F ring is so consistently shaped, even though various things are constantly acting to perturb it. In particular, Prometheus periodically plunges into the F ring, drawing out dramatic streamers and fans. In fact, Prometheus and Pandora, far from behaving as shepherds, actually act to stir up the motions of particles in most of the region near the F ring. Furthermore, there are other bodies that Cassini has spotted in the F ring region whose behavior is so chaotic that it's been hard to follow them; these things have "violent collisional interactions with the F ring core," so, all in all, it's really difficult to explain why the core of the F ring generally looks the same as it has ever since the Voyagers passed by.
The orbit of Prometheus precesses. In other words, the point of this moon's closest approach to Saturn keeps slowly moving around. So, the period with which this moon orbits Saturn is slightly different than the period with which it moves in and out from Saturn. A 'Lindblad resonance' happens when a chunk of ice goes around Saturn exactly once each time Prometheus goes in and out! Lakdawalla writes:
So: consider a moon and a ring particle orbiting Saturn. We don't care (for the moment) what the orbital periods of the moon and ring particles are; what we do care about is the "in-and-out" period of the ring particle in its orbit. You have a Lindblad resonance if, every time the moon passes by the ring particle, the ring particle happens to be on the same position in its in-and-out motion.
The full story is even more complicated than that — obviously, since it has to explain all the weird patterns in the picture here. The F ring consists of several strands, which braid around each other, and have strange kinks in them:
But I'll let you read Lakdawalla's blog for more:
What I really want to tell you is some other news: how the F ring was formed in the first place!
It's in an interesting place. Any moon too close to Saturn would be broken up by tidal forces unless it was held together by forces stronger than gravity. The fluid Roche limit says how close is too close: it's 147,000 kilometers from the center of Saturn. The F ring is 140,180 kilometers from the center of Saturn. So it's just within the fluid Roche limit. Pandora and Prometheus are within that limit too — but being at least slightly rigid, they can avoid being stretched and broken apart.
That could be a clue. But how did the F ring actually form? A new paper says it was created by a collision between Prometheus and Pandora! The authors write:
Saturn's F ring is a narrow ring of icy particles, located 3,400 km beyond the outer edge of the main ring system. Enigmatically, the F ring is accompanied on either side by two small satellites, Prometheus and Pandora, which are called shepherd satellites. The inner regular satellites of giant planets are thought to form by the accretion of particles from an ancient massive ring and subsequent outward migration. However, the origin of a system consisting of a narrow ring and shepherd satellites remains poorly understood. Here we present N-body numerical simulations to show that a collision of two of the small satellites that are thought to accumulate near the main ring.s outer edge can produce a system similar to the F ring and its shepherd satellites. We find that if the two rubble-pile satellites have denser cores, such an impact results in only partial disruption of the satellites and the formation of a narrow ring of particles between two remnant satellites. Our simulations suggest that the seemingly unusual F ring system is a natural outcome at the final stage of the formation process of the ring-satellite system of giant planets.
If so, the F ring and these moons have been engaged in a drama for millions of years, starting with the very formation of Saturn's rings. We missed the beginning of the show.
The paper is here, but it ain't free:
Abstract: The long-term stability of the narrow F Ring core has been hard to understand. Instead of acting as 'shepherds', Prometheus and Pandora together stir the vast preponderance of the region into a chaotic state, consistent with the orbits of newly discovered objects like S/2004 S 6. We show how a comb of very narrow radial locations of high stability in semimajor axis is embedded within this otherwise chaotic region. The stability of these semimajor axes relies fundamentally on the unusual combination of rapid apse precession and long synodic period which characterizes the region. This situation allows stable 'antiresonances' to fall on or very close to traditional Lindblad resonances which, under more common circumstances, are destabilizing. We present numerical integrations of tens of thousands of test particles over tens of thousands of Prometheus orbits that map out the effect. The stable antiresonance zones are most stable in a subset of the region where Prometheus first-order resonances are least cluttered by Pandora resonances. This region of optimum stability is paradoxically closer to Prometheus than a location more representative of 'torque balance', helping explain a longstanding paradox. One stable zone corresponds closely to the currently observed semimajor axis of the F Ring core. While the model helps explain the stability of the narrow F Ring core, it does not explain why the F Ring material all shares a common apse longitude; we speculate that collisional damping at the preferred semimajor axis (not included in the current simulations) may provide that final step. Essentially, we find that the F Ring core is not confined by a combination of Prometheus and Pandora, but a combination of Prometheus and precession.Whew — that's complicated!
By the way, S/2004 S 6 is a weird little thing they've discovered in the F ring. Nobody even knows if it's solid or just a clump of dust. You can see it here:
Here is another shot of Prometheus and the F ring:
You can see it stealing ice from the F ring! By the way, I shaded all
these pictures blue just for artistic effect; they were black and white.
Click on the pictures for the originals.
August 28, 2015
There's a game called Robocraft where you try to destroy your enemy's "protonium reactors". These are imaginary devices powered by imaginary "protonium crystals". But I think reality is cooler than any fantasy, so I'm not interested in that crap. I'm interested in actual protonium!
Protonium is a blend of matter and antimatter. It's a kind of exotic atom made of a proton and an antiproton. A proton is positively charged, so its antiparticle, the antiproton, is negatively charged. Opposite charges attract, so a proton and an antiproton can orbit each other. That gives protonium.
A proton and an electron can also orbit each other, and that's called hydrogen. But there are a few big differences between hydrogen and protonium.
First, hydrogen lasts forever, but protonium does not. When they meet, the proton and antiproton annihilate each other. How long does it take for this to happen? It depends on how they're orbiting each other.
In both hydrogen and protonium, various orbits are possible. Particles are really waves, so these orbits are really different wave patterns, like different ways a trampoline can wiggle up and down. These patterns are called orbitals.
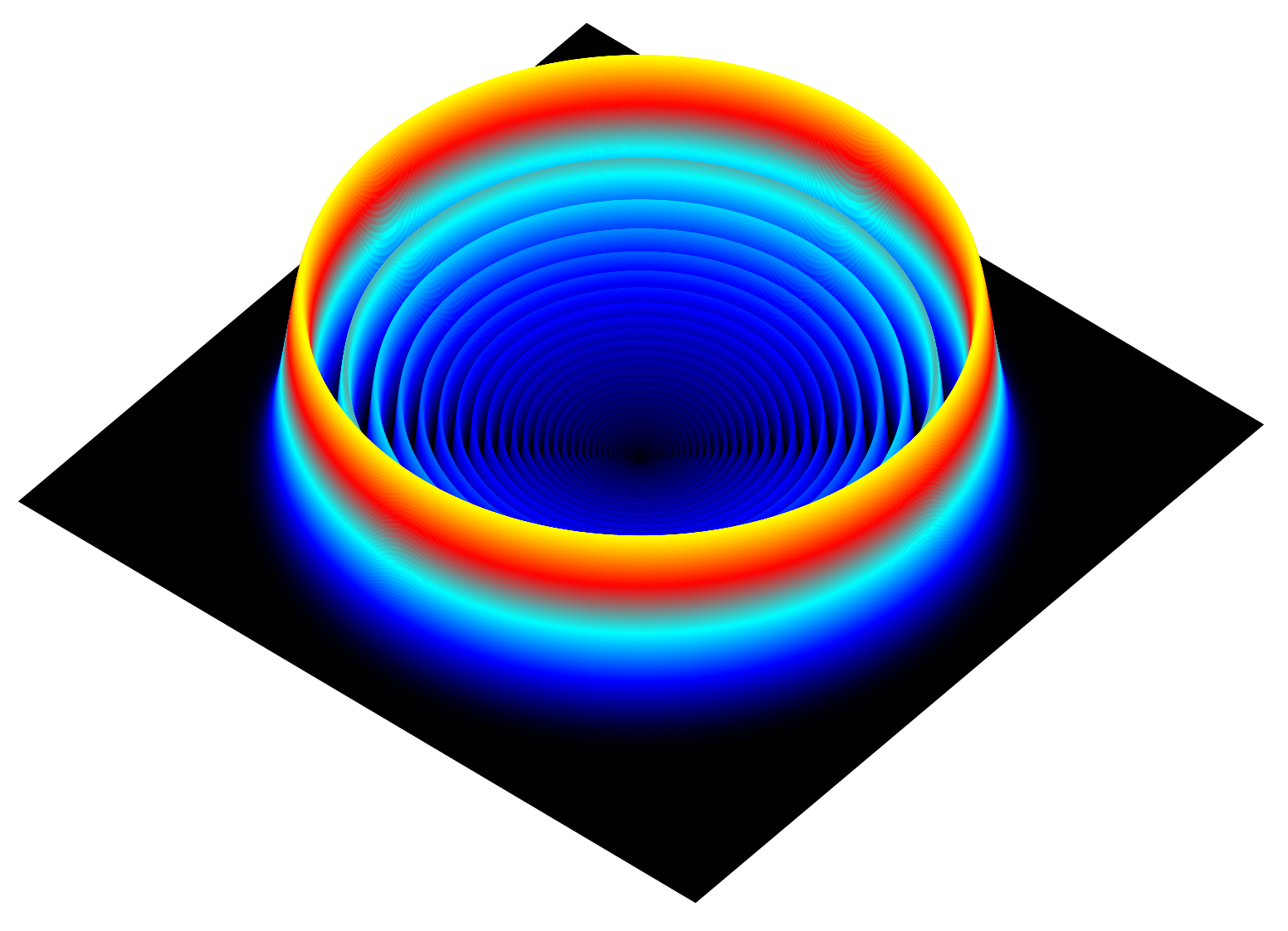
Orbitals are labelled by numbers called quantum numbers. If a hydrogen atom isn't spinning at all, it will be spherically symmetric. Then you just need one number, cleverly called n, to say what its wave pattern looks like.
The picture here shows the orbital with n = 30. It has 30 wiggles as you go from the center outwards. It's really 3-dimensional and round, but the picture shows a circular slice. The height of the wave at some point says how likely you are to find the electron there. So, the electron is most likely to be in the orange region. It's very unlikely to be right in the middle, where the proton sits.
The same math works for protonium! There's another big difference to keep in mind: the proton and antiproton have the same mass, so they both orbit each other. But we can track just one of them, moving around their shared center of mass. Then protonium works a lot like hydrogen. You get spherically symmetric orbitals, one for each choice of that number called n.
So: if you can make protonium in a orbital where n = 30, it's unlikely for the two protons to meet each other. Gradually your protonium will emit light and jump to orbitals with lower n, which have less energy. And eventually the proton and antiproton will meet... and annihilate in a flash of gamma rays, which are just a powerful form of light.
How long does this take? For n = 30, about 1 microsecond. And if you make protonium with n = 50, it lasts about 10 microseconds.
That doesn't sound long, but in particle physics it counts as a pretty long time. Probably not long enough to make protonium crystals, though!
Protonium was first made around 1989. Around 2002 people made a lot of it using the Antiproton Decelerator at CERN. This is just one of the many cool gadgets they keep near the Swiss-French border.
You see, to create antimatter you need to smash particles at each other at almost the speed of light — so the antiparticles usually shoot out really fast. It takes serious cleverness to slow them down and catch them without letting them bump into matter and annihilate.
But they made protonium by accident in 2002 and only realized it 4 years later. They were trying to make antihydrogen, which is the antiparticle of an electron orbiting an antiproton. They did this by creating a bunch of antiprotons and slowing them down. Once they managed to do this, they caught the antiprotons in a Penning trap. This holds charged particles using magnetic and electric fields. Then they cooled the antiprotons — slowed them even more — by letting them interact with a cold gas of electrons. Then they mixed in some positrons. And they got antihydrogen! But they also made some protonium, by accident.
The folks at CERN have also made antiprotonic helium, which is an antiproton orbiting a helium atom with one electron removed! The antiproton acts a bit like the missing electron, except that it's 1836 times heavier, so it must orbit much closer to the helium nucleus.
There are even wackier forms of matter in the works — or at least, in the dreams of theoretical physicists. But that's another story for another day.
Here's the 2006 paper about protonium:
The child in me thinks it's really cool that there's an abbreviation for protonium, Pn, just like a normal element.
Puzzle 1: about how big is protonium in its n = 1 orbital, compared to hydrogen in its n = 1 orbital? I've given you all the numbers you need to estimate this, though not all the necessary background in physics.
In Puzzle 1 you're supposed to assume protonium in its n = 1 state is held together by the attraction of opposite charges, just like hydrogen. But is that true? If the proton and antiproton are too close, they'll interact a lot via the strong force!
Puzzle 2: The radius of hydrogen in its n = 1 state is about 50,000 femtometers, while the radius of a proton is about 1 femtometer. Using your answer to Puzzle 1, compare the radius of protonium in its n = 1 orbital to the radius of a proton.
If protonium is a lot bigger than a proton, it's probably held together mostly in the same way as hydrogen: by the electromagnetic force.
For answers to the puzzles, and other cool facts, read the comments on my G+ post.
For my September 2015 diary, go here.