
If you get stuck, you can read the Mathematica code on his website, or check
out the comments on my G+ post. But it's probably more fun to watch it carefully and see for yourself!
The British mathematician James Joseph Sylvester, who lived from 1814
to 1897, was one of the first to dig deeply into the beautiful
patterns you can form using finite sets. But he got into lots of
trouble.
For example, he entered University College London at the age of 14.
But after just five months, he was accused of threatening a fellow
student with a knife in the dining hall! His parents took him out of
college and waited for him to grow up a bit more.
He began studies in Cambridge at 17. Despite being ill for 2 years,
he came in second in the big math exam called the tripos. But he
couldn't get a degree... because he was Jewish.
After just a few months, a student reading a newspaper in one of
Sylvester's lectures insulted him. Sylvester struck him with a sword
stick. The student collapsed in shock. Sylvester thought he'd killed
the guy! He fled to New York where one of his brothers was living.
Later he came back. According to the online
biography I'm reading, "the abuse suffered by Sylvester from this
student got worse after this". Soon he quit his job.
He returned to England and took up a job at a life insurance company.
He needed a law degree for this job, and in his studies he met another
mathematician, five years younger, studying law: Cayley! They worked
together on matrices and invariant theory.
Sylvester only got another math job in 1855, at the Royal Military
Academy of Woolwich. He was 41. At age 55 they made him retire
— that was the rule — but for some reason the school
refused to pay his pension!
The Royal Military Academy only relented and paid Sylvester his
pension after a prolonged public controversy, during which he took his
case to the letters page of The Times.
When he was 58, Cambridge University finally gave him his BA and MA.
At age 62, Sylvester went back to the United States to become the
first professor of mathematics at the newly founded Johns Hopkins
University in Baltimore, Maryland. His salary was $5,000 — quite
generous for the time.
He demanded to be paid in gold.
They wouldn't pay him in gold, but he took the job anyway. At age 64,
he founded the American Journal of Mathematics. At 69, he was invited
back to England to become a professor at Oxford. He worked there until
his death at age 83.
One thing I like about Sylvester is that he invented lots of terms for
mathematical concepts. Some of them have caught on: matrix,
discriminant, invariant, totient, and Jacobian! Others have not:
cyclotheme, meicatecticizant, tamisage and dozens more.
Among many other things, Sylvester discovered soe special
features of 6-element sets. Sylvester defined a 'duad' to be a way of
choosing 2 things from a set. A set of 6 things has 15 duads. A
hypercube has 16 corners. The picture by Greg Egan above shows a hypercube with
15 of its 16 corners labelled by duads. The bottom corner is
different.
This may seem just cute, but in fact it can help you visualize a
rather wonderful fact: the group of permutations of 6 things is
isomorphic to the symmetry group of a 4-dimensional symplectic vector
space over the field with 2 elements.
For details, read this:
While I've told you some of the tawdry details of Sylvester's life,
like any great mathematician he spent muxh of his life immersed
in worlds of abstract beauty.
He also loved poetry, and translated poems into English from French,
German, Italian, Latin and Greek.
This Friday I was hanging out and drinking beer with some philosophy
professors. This is always fun, because they think sort of like me,
but different. They seem more optimistic about our ability to solve
all sorts of puzzles just by talking.
To annoy them a bit, I said that philosophers are great at verbal
reasoning, but mathematicians should be good at three kinds of
reasoning: verbal, symbolic and visual reasoning.
In response, one of them showed me this picture proof that
\(\sqrt{2}\) is irrational.
We just need to show that it's impossible to have
$$ a^2 = b^2 + b^2 $$
for whole numbers \(a\) and \(b\). So let's do a proof by contradiction. We
can assume \(a\) is the smallest whole number that obeys this equation for
some whole number \(b\). We'll get a contradiction by finding an even
smaller one.
We do it by drawing a picture.
The big square in this picture is an \(a \times a\) square. The two
light blue squares, which overlap in the middle, are \(b \times b\) squares.
The area of the big square is the sum of the areas of the light blue
squares. But there are two problems. First, the light blue squares
overlap. Second, they don't cover the whole big square! These two
problems must exactly cancel out.
So, the area of the overlap — the dark blue squares — must
exactly equal the area that's not covered — the two pink
squares.
So, the area of the dark blue square is the sum of the areas of the
pink squares! But the lengths of the sides of these must be whole
numbers, say \(c\) and \(d\). So we have
$$ c^2 = d^2 + d^2 $$
But \(c\) is smaller than \(a\). So, we get a contradiction!
Actually this proof uses a mix of verbal and visual reasoning, with
just a tiny touch of symbolic reasoning. I wrote the formulas like
\(a^2 = b^2 + b^2\) just to speed things up a bit and reassure you that
this was math. I didn't really do anything with them.
The philosophers who told me about this are Mike Pelczar and Ben Blumson. The picture here comes from a website Mike pointed me to:
Richeson says:
On the other hand, Ben says John Bigelow published the proof in his
book The Reality of Numbers in 1988, without citing anyone.
We wondered if it was known to the ancient Greeks.
You can do similar proofs of the irrationality of \(\sqrt{3}, \sqrt{5},
\sqrt{6}\) and \(\sqrt{10}\):
And this particular style of proof by contradiction is famous! It's
called proof by infinite descent. You assume you have the smallest
whole number that's a counterexample to something you want to prove,
and then you cook up an even smaller one. It's really just
mathematical induction in disguise, but it's more fun. It was
developed by Pierre Fermat — who, by the way, was a lawyer.
If you want to take all the fun out of the proof I just gave, you can
do it like this.
Assume \(a\) is the smallest whole number for which there's a whole
number \(b\) with
$$ a^2 = b^2 + b^2 $$
Let
$$c = 2b - a$$
and
$$d = a - b$$
Then \(c\) and \(d\) are whole numbers and
$$ c^2 = d^2 + d^2 $$
(You can do some algebra to check this.) But \(c \lt a\), so we get a
contradiction.
Wikipedia shows you how to prove by infinite descent that whenever \(n\)
is a whole number, either \(\sqrt{n}\) is a whole number or it's irrational:
Fermat did a lot more interesting stuff with this method, too!
Right now physicists are struggling with the 'firewall paradox'
— a problem in our theory of black holes. But this is far from
the first time physicists have been stuck with an annoying 'paradox'.
Back in the late 1800s, physicists noticed that an electron should get
mass from its electric field. Nowadays we'd say this is obvious. The
electric field has energy, and \(E = mc^2\), so it contributes to the mass
of the electron. But this was before special relativity!
How did they figure it out? They were very clever. They used
Newton's \(F = ma\). When you push on something with a force, you can
figure out its mass by seeing how much it accelerates!
So, they did some calculations. When you push on an electron with a
force, you also affect its electric field. It's like the electron has
a cloud around it, that follows wherever the electron goes. This
makes it harder to accelerate the electron. So, it effectively
increases the electron's mass. They calculated this extra mass.
They also did an easier calculation: how much energy this electric field has!
Say \(m\) is the extra mass due to the electric field surrounding the
electron, and \(E\) is the energy of this electric field. Then they
discovered that
$$ E = \frac{3}{4} mc^2 $$
Whoops!
Had they made an algebra mistake? Not really.
Some really smart people all got the same answer! Oliver Heaviside
got it in 1889 — he was one of the world's smartest electrical
engineers. J.J. Thomson got it in 1893 — he's the guy who
discovered the electron! Hendrik Lorentz kept getting the same
answer, even as late as 1904 — and he's one of the people who
paved the way for relativity!
But in 1905, Einstein wrote his paper showing that \(E = mc^2\) is the only
possible answer that makes sense.
So what went wrong?
All those guys were assuming the electron was a little sphere of
charge. Why? In their calculations, if was a point, the energy in
its electric field would be infinite, because the electric field gets
extremely strong near that point. The mass contributed by this field
would also be infinite.
If the electron were a tiny sphere, they could avoid those infinite answers.
But then they ran into this \(E = \frac{3}{4}mc^2\) problem. Why? Because
electrical charges of the same sign repel each other. So a tiny
sphere of charge would explode if something weren't holding it
together. And that something — whatever it is — might
have energy. But their calculation ignored that extra energy.
In short, their picture of the electron as a tiny sphere of charge,
with nothing holding it together, was incomplete. And their
calculation showing \(E = \frac{3}{4}mc^2\), together with special
relativity saying \(E = mc^2\), shows this incomplete picture is
inconsistent.
So in the end, it's not a case of people being stupid. It's a case of
people discovering something interesting... by taking a plausible idea
and showing it can't work.
If you want the details, read what Feynman has to say:
Here's a bit of what he says:
In deriving our equations for energy and momentum, we assumed the
conservation laws. We assumed that all forces were taken into account
and that any work done and any momentum carried by other
'nonelectrical' machinery was included. Now if we have a sphere of
charge, the electrical forces are all repulsive and an electron would
tend to fly apart. Because the system has unbalanced forces, we can
get all kinds of errors in the laws relating energy and momentum. To
get a consistent picture, we must imagine that something holds the
electron together. The charges must be held to the sphere by some kind
of rubber bands.something that keeps the charges from flying off. It
was first pointed out by Poincaré that the rubber bands — or
whatever it is that holds the electron together — must be included in
the energy and momentum calculations. For this reason the extra
nonelectrical forces are also known by the more elegant name "the
Poincaré stresses". If the extra forces are included in
the calculations, the masses obtained in two ways are changed (in a
way that depends on the detailed assumptions). And the results are
consistent with relativity; i.e., the mass that comes out from the
momentum calculation is the same as the one that comes from the energy
calculation. However, both of them contain two contributions: an
electromagnetic mass and contribution from the Poincaré
stresses. Only when the two are added together do we get a consistent
theory.
This was a bummer back around 1905, because people had actually hoped
all the mass of the electron was due to its electric field. Note:
this extra assumption is not required for the \(E = \frac{3}{4}mc^2\)
problem to bite you in the butt. It's already a problem that the
energy due to the electric field is \(\frac{3}{4}mc^2\) where \(m\) is the
mass due to the electric field. But the solution to the problem
— extra 'rubber bands' — killed the hope that the electron
could be completely understood using electromagnetism.
It is therefore impossible to get all the mass to be electromagnetic
in the way we hoped. It is not a legal theory if we have nothing but
electrodynamics. Something else has to be added. Whatever you call
them — 'rubber bands', or 'Poincaré stresses', or
something else — there have to be other forces in nature to make a
consistent theory of this kind.
Wikipedia has a good article on the history of this problem:
and this paper is also good:
The spacecraft Dawn has gotten a closer look at the mysterious white
spots on the asteroid Ceres. In the first photos, they were so bright
they were overexposed!
Now Dawn is closer. Here's the biggest patch of white stuff, called
Spot 5, in a crater called Occator.
What is it? The obvious guess is some sort of ice or salt, reflecting
sunlight. But here's the cool part: you can sometimes see haze over
Spot 5. This suggests that some sort of gas is coming up from beneath
the surface! Or maybe the ice is sublimating, turning into
vapor... perhaps explosively?
The mission director writes:
This picture is a composite of two images: one using a short
exposure that captures the detail in the bright spots, and one where
the background surface is captured at normal exposure. Each pixel
here is a 140 meter × 140 meter square.
Right now Dawn is orbiting Ceres at a distance of 1450 kilometers. In
December, it will descend to just 375 kilometers from the surface.
Then we'll get even better images!
And when the mission ends? Then Dawn will remain as a permanent
satellite of Ceres. A fitting end to a great mission — it's the first
spacecraft to orbit two bodies, Vesta and Ceres.
You can watch a short video of what Dawn has been seeing, here:
This image came from here:
For more on the haze, read this:
.png)
Apparently the proof was discovered by Stanley Tennenbaum in the
1950's but was made widely known by John Conway around 1990. The proof
appeared in Conway's chapter "The Power of Mathematics" of the book
Power, which was edited by Alan F. Blackwell, David MacKay (2005).

He does all the calculations that explain this problem. I've been
reading his books since high school, but never really understood this
part until now. I'm thinking about problems with infinity in physics.
The discrepancy between the two formulas for the electromagnetic mass
is especially annoying, because we have carefully proved that the
theory of electrodynamics is consistent with the principle of
relativity. [...] So we are in some kind of trouble; we must have
made a mistake. We did not make an algebraic mistake in our
calculations, but we have left something out.
All this is part of a longer story I told later:
Dawn has transformed what was so recently a few bright dots into a
complex and beautiful, gleaming landscape. Soon, the scientific
analysis will reveal the geological and chemical nature of this
mysterious and mesmerizing extraterrestrial scenery.
September 14, 2015

This is based on a famous print by M. C. Escher called 'Ascending and Descending'. That in turn was based on an idea by the mathematician Penrose, called the Penrose stairs. But Penrose in turn was inspired by Escher, who was inspired by Penrose.... in an endless loop!
At least that's the story on Wikipedia:
At an Escher conference in Rome in 1985, Roger Penrose said that he had been greatly inspired by Escher's work when he and his father discovered the Penrose stairs.
Penrose said he'd first seen Escher's work at a conference in Amsterdam in 1954. He was "absolutely spellbound", and on his journey back to England he decided to produce something "impossible" on his own. After experimenting with various designs he finally arrived at the impossible Penrose triangle.
Roger Penrose then showed his drawings to his father Lionel, who immediately produced several variants, including the impossible stairs. They wanted to publish their findings but didn't know where to do it. Because Lionel Penrose knew the editor of British Journal of Psychology, the finding was finally presented as a paper there. After its publication in 1958, they sent a copy of the article to Escher as a token of their esteem.
But here's the weird part. While the Penroses credited Escher in their article, Escher himself noted in a letter to his son in January 1960 that he was:
... working on the design of a new picture, which featured a flight of stairs which only ever ascended or descended, depending on how you saw it. They form a closed, circular construction, rather like a snake biting its own tail. And yet they can be drawn in correct perspective: each step higher (or lower) than the previous one. I discovered the principle in an article which was sent to me, and in which I myself was named as the maker of various 'impossible objects'. But I was not familiar with the continuous steps of which the author had included a clear, if perfunctory, sketch..."
So it seems this impossible staircase willed itself into existence in a paradoxical loop of causality!
But now that I think about it, all good ideas come into being a bit like this. At first they exist only in vague form, in the random jostlings of thoughts and words. They exist just a little, merely because they can exist. But thanks to their power, the more people think and talk about them, the more they spiral into existence... until finally they are clear and undeniable. Like this idea here.
Puzzle 1: just by looking carefully at this animated gif, can you guess who made it?
Puzzle 2: can you see the slight mistake in the picture here?
Puzzle 3: does that mistake occur in Escher's original print? Here's the original

Here's the Wikipedia article where I got the story:
For answers to the puzzles, see the comments on my G+ post.
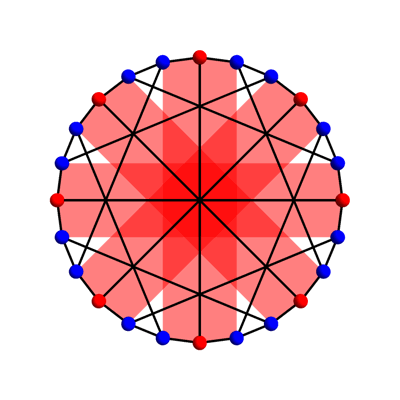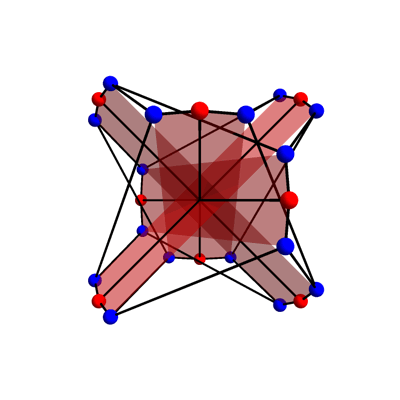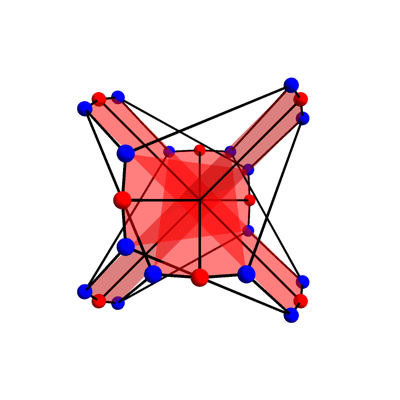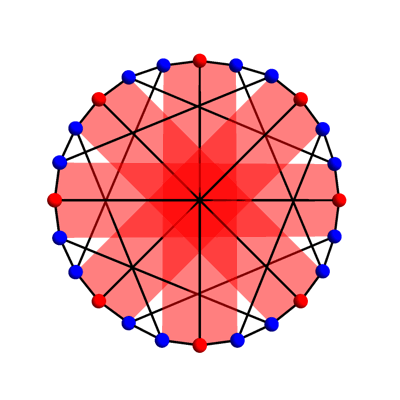
This is the McGee graph. You'll notice each vertex has 3 neighbors. Also, if you go around a cycle of edges, there will always be at least 7 edges in your path. The McGee graph's claim to fame is that it has the fewest vertices possible for a graph with these two properties.
This isn't so amazing, so the McGee graph is not as famous as some others I've discussed on Visual Insight. It's fairly symmetrical, though. Besides the obvious symmetries — rotating it 1/8 of a turn, or flipping it over — there are some sneaky symmetries, like the one shown in this animation by Greg Egan.
He drew four red 'bands', actually hexagons, because this sneaky symmetry mixes up the nodes in each 'band' in a clever way. Also, you'll notice that some vertices are red, and others blue. That's because all the symmetries send red vertices to red ones, and blue vertices to blue ones.
In trying to understand the McGee graph better, I wanted to start by understanding its symmetries. It has 8 rotational symmetries; if we throw in our ability to flip it over we get a total of 16, and if we throw in all the sneaky symmetries we get a total of 32.
There are lots of different groups with 32 elements. In fact, there are 51 of them.
(If you start listing finite groups, you'll soon discover that most of them have a power of 2 as their number of elements. Indeed, of the 50 billion or so groups of size at most 2000, more than 99% have 1024 elements!)
Luckily there's an online list of all 51 groups with 32 elements, and a fellow named Gordon Royle told me which of these was the symmetry group of the McGee Graph. So, I soon found out that the symmetries of the McGee graph are the affine transformations of the integers mod 8.
I should explain this. An affine transformation is something like this: $$ x \mapsto ax + b $$ where \(a\) is invertible. You may be used to calling them 'linear', but showoffs like me prefer to save that word for transformations of this sort: $$ x \mapsto ax $$ Anyway, you may be used to affine transformations when \(x, a,\) and \(b\) are real numbers. The real numbers form a line. The affine transformations just slide, stretch or squash, and maybe flip that line.
But here we are dealing with the case where \(x, a,\) and \(b\) are integers mod 8. What is the 'line' like then? Well, the integers mod 8 can be visualized as an octagon — that is, the 8 red nodes in the animation here. So now our 'line' looks like an octagon!
This may freak you out, but to mathematicians there's nothing more fun than taking intuitions from a familiar example and applying them to some weird other situation. So now a line looks like an octagon? — sure, we can handle that.
What are affine transformations like? Well, these are rotations of the octagon: $$ x \mapsto x + b $$ We can also flip the octagon like this: $$ x \mapsto -x $$ But there are other transformations of this sort: $$ x \mapsto ax $$ where \(a\) isn't \(1\) or \(-1\), and those are the 'sneaky symmetries'.
You can check that in the integers mod 8, only four numbers are invertible: \(1, 3, 5\) and \(7 = -1\). So, we get \(4 \times 8 = 32\) affine transformations. And those are the symmetries of the McGee graph!
So: the red vertices of the McGee graph are just integers mod 8. The symmetries are affine transformations. Then the question becomes: how can we understand the blue vertices, and the edges, in terms of the integers mod 8? If we answer this correctly, it will become obvious why affine transformations give symmetries of the McGee graph.
This is a fun puzzle for people who like Felix Klein's philosophy relating groups and geometry. Egan and I worked out the answer, and explained it — with lots of pictures — on my blog Visual Insight:
So go there if you want the full story.
Not coincidentally, all the groups of size \(\le 2000\) were listed in the year 2000. You can read more about them here:
This is a rock formation made of chalk in the Sahara el Beyda, or White Desert, in Egypt. This beautiful place got in the news recently after 8 Mexican tourists were killed there by Egyptian security forces, who apparently mistook them for terrorists.
But let's leave the sad world of mankind for a minute, and enjoy the desert.
There are actually many mushroom-shaped rocks like this in the White Desert.
Why?
Try to guess.
Okay: they are ventifacts, meaning they are carved by wind-blown sand. Even in strong winds, sand grains don't usually stay in the air for long. Instead they bounce along the ground. So, they cut deeper into the bottom of the rock than the top!
Magical-looking, but not magic.
This photo was taken by Christine Schultz.
September 29, 2015

This looks like a deerbunny — with dark, soulful eyes! But it's a mara, from South America. It eats grass. It can run up to 30 kilometers per hour, but it can also hop like a rabbit or make long jumps. It's shy in the wild. But it can be quite friendly if raised with people from a young age. Some people keep them as pets.
The mara is the world's fourth largest rodent, after capybaras, beavers, and porcupines. But they're more closely related to guinea pigs.
They're common in the Patagonian steppes of Argentina, but they also live in Paraguay and other places.
This photo was taken by Dick Klees, and I saw it here: