It looks suspiciously like a circle. But the regular 65537-gon is famous. Gauss proved you can construct a regular \(n\)-gon with straight-edge and compass if \(n\) is a prime of the form \(2^{2^k} + 1\). These are called Fermat primes. These are all the Fermat primes known in Gauss' day: $$ \begin{array}{ll} 2^1 + 1 & = 3 \\ 2^2 + 1 & = 5 \\ 2^4 + 1 & = 17 \\ 2^8 + 1 & = 257 \\ 2^{16} + 1 & = 65537 \end{array} $$ Even earlier, Gauss had constructed the 17-gon in 1796. The 257-gon was first constructed in 1822 by Magnus Georg Paucker. And the first to show how to construct the 65537-gon was Johann Gustav Hermes, in 1894. It took him 10 years!
It seems Hermes, ironically named after the Greek god of speed, spent a whole decade writing a 200-page manuscript explaining how to construct a regular 65537-gon with ruler and compass. But this paper of his is just 16 pages long:
If you take Pascal's triangle mod 2 and draw black for 1 and white for 0, you get a pleasing pattern.... closely connected to a fractal called the Sierpinski gasket, where you keep cutting out triangular holes from an equilateral triangle:
The rows of Pascal's triangle mod 2 give numbers in binary: $$ \begin{array} {cl} 1 & = 1 \\ 11 & = 3 \\ 101 & = 5 \\ 1111 & = 15 \\ 10001 & = 17 \\ 110011 & = 51 \\ 1010101 & = 85 \\ 11111111 & = 255 \\ 100000001 & = 257 \\ \end{array} $$ and so on. And the first 32 of these numbers are precisely all the odd numbers \(n\) we know for which you can construct a regular \(n\)-gon using straight-edge and compass!
They're the products of distinct Fermat primes \(3, 5, 17, 257\) and \(65537\). Here they are in detail, from the Online Encyclopedia of Integer Sequences wiki:
We only know 5 Fermat primes: for example, the next Fermat number is not prime: $$ 2^{32} + 1 = 4294967297 = 641 \times 6700417 $$ So, we only know \(2^5 = 32\) products of distinct Fermat primes. And it's known that a regular \(n\)-gon with \(n\) odd is constructible by straight-edge and compass iff \(n\) is a product of distinct Fermat primes!
As a result, we only 32 regular polygons with an odd number of sides that can be constructed by straight-edge and compass: the polygons with \(1\), \(3\), \(5\), \(15\), \(17\), \(51\), \(85\), \(255\), \(257\), \(771\), \(1285\), \(3855\), \(4369\), \(13107, 21845\), \(65535\), \(65537\), \(196611\), \(327685\), \(983055\), \(1114129\), \(3342387\), \( 5570645\), \(16711935\), \(16843009\), \(50529027\), \(84215045\), \(252645135\), \(286331153\), \(858993459\), \(1431655765\), and \(4294967295\) sides.
For more, see my blog article:
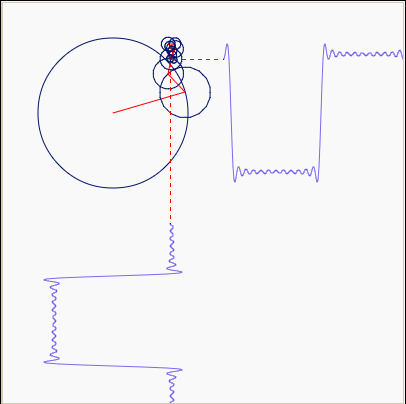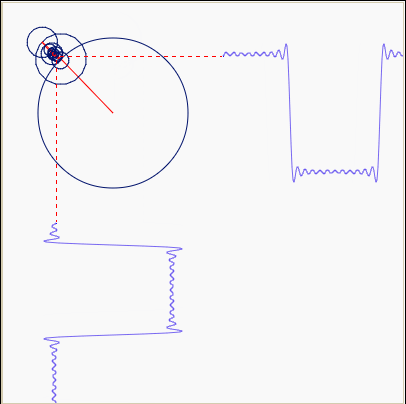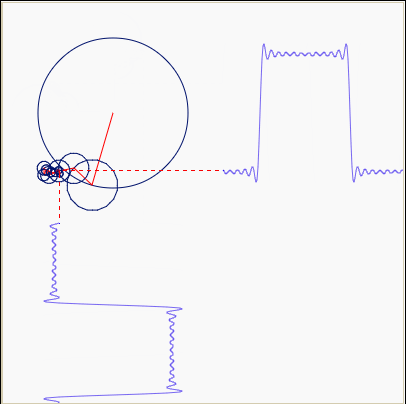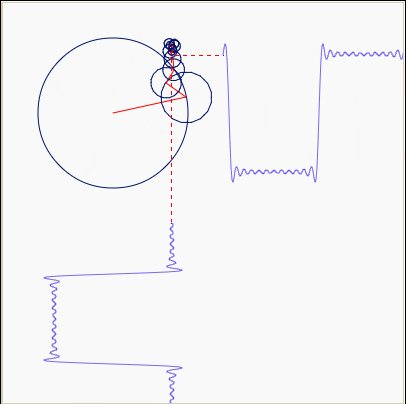
People like to make fun of epicycles because you can describe any orbit using epicycles. Above we see an almost square orbit done using epicycles.
But this weakness is also their strength: a Fourier series is a way
of writing any periodic function using epicycles.
February 16, 2019

My former student Brandon Coya discovered this "commutative law". It can't be new. It's easy to prove. But I'll name it after him. My student Joe Moeller quickly noticed that the operation \( x \#y = x^{\ln y}\) is also associative and obeys \(e\#x = x\).
Over on Twitter, someone noticed that this operation distributes over multiplication: $$ x \# (yz) = (x \# y)(x \# z) $$ and obeys $$ x \# 1 = 1 $$
See what's going on? The key is that
$$ x \# y = e^{\ln x \ln y} $$
so exponentiation provides a bijection between \( \mathbb{R} \) and
the set of positive real numbers, which carries addition and multiplication
of real numbers to the multiplication and the \(\#\) operation on positive
real numbers. Thus, the set of positive real numbers becomes a field
with multiplication as its addition, \(\#\) as its multiplication,
\(1\) as its additive identity and \(e\) as its multiplicative identity!
February 23, 2019
The Milky Way is a spiral galaxy, so it has spiral arms. We are in the inner edge of the Orion Arm. You can see the Orion Arm from here! This photo of the Orion Arm was taken by Ahmed abd Elkader Mohamed in Sinai, Egypt.
The Orion Arm is between the Sagittarius Arm, closer to to the galactic center, and the Perseus Arm. It may be a mere 'spur' connecting these arms — that's what the picture below calls it. Or it may be a truly separate arm. This seems to be the more popular view today.
It seems the 'density wave' theory of spiral arms is still controversial, but it says stars orbiting the galactic center temporarily bunch up to form arms. If so, a given star doesn't stay in the same arm forever.
In fact, most stars within 1000 parsecs of the Sun belong to 5 or more 'streams': groups with similar velocity. The most well-established are the Coma Berenices, Pleiades, Hyades, Sirius and Hercules streams. Here are the U (radial) and V (angular) components of their velocities.
The paper where I got this graph argues that Oumuamua, the interstellar asteroid that shot past us last year, is part of the Pleiades stream! Its velocity looks right.
This is the paper:
In short: the Milky Way is a complex and lively place, though it operates on majestically slow time scales. The Sun has orbited the Galaxy only 20 times in its life so far!