

From the New York Times article by Allan Kozinn:
Always intent on expanding the Beatles. horizons, Mr. Martin began chipping away at the group's resistance to using orchestral musicians on its recordings in early 1965. While recording the Help! album that year, he brought in flutists for the simple adornment that enlivens Lennon's "You've Got to Hide Your Love Away," and he convinced Mr. McCartney, against his initial resistance, that "Yesterday" should be accompanied by a string quartet.For more, see:A year later, during the recording of the album Revolver, Mr. Martin no longer had to cajole: The Beatles prevailed on him to augment their recordings with arrangements for strings (on "Eleanor Rigby"), brass (on "Got to Get You Into My Life"), marching band (on "Yellow Submarine") and solo French horn (on "For No One"), as well as a tabla player for Harrison's Indian-influenced song "Love You To".
It was also at least partly through Mr. Martin's encouragement that the Beatles became increasingly interested in electronic sound. Noting their inquisitiveness about both the technical and musical sides of recording, Mr. Martin ignored the traditional barrier between performers and technicians and invited the group into the control room, where he showed them how the recording equipment at EMI's Abbey Road studios worked. He also introduced them to unorthodox recording techniques, including toying with tape speeds and playing tapes backward.
Mr. Martin had used some of these techniques in his comedy and novelty recordings, long before he began working with the Beatles.
"When I joined EMI," he told The New York Times in 2003, "the criterion by which recordings were judged was their faithfulness to the original. If you made a recording that was so good that you couldn't tell the difference between the recording and the actual performance, that was the acme. And I questioned that. I thought, O.K., we're all taking photographs of an existing event. But we don't have to make a photograph; we can paint. And that prompted me to experiment."
Soon the Beatles themselves became intent on searching for new sounds, and Mr. Martin created another that the group adopted in 1966 (followed by many others). During the sessions for "Rain", Mr. Martin took part of Lennon's lead vocal and overlaid it, running backward, over the song's coda.
"From that moment," Mr. Martin said, "they wanted to do everything backwards. They wanted guitars backwards and drums backwards, and everything backwards, and it became a bore." The technique did, however, benefit "I'm Only Sleeping (with backward guitars) and "Strawberry Fields Forever (with backward drums).
Mr. Martin was never particularly trendy, and when the Beatles adopted the flowery fashions of psychedelia in 1966 and 1967 he continued to attend sessions in a white shirt and tie, his hair combed back in a schoolmasterly pre-Beatles style. Musically, though, he was fully in step with them. When Lennon wanted a circus sound for his "Being for the Benefit of Mr. Kite," Mr. Martin recorded a barrel organ and, following the example of John Cage, cut the tape into small pieces and reassembled them at random. His avant-garde orchestration and spacey production techniques made "A Day in the Life" into a monumental finale for the kaleidoscopic album Sgt. Pepper's Lonely Hearts Club Band.
The computer program AlphaGo just won its third game against the excellent Korean player Lee Sedol.
But what would it feel like to watch one of these games, if you're good at go? David Ormerod explains:
It was the first time we'd seen AlphaGo forced to manage a weak group within its opponent's sphere of influence. Perhaps this would prove to be a weakness?This, however, was where things began to get scary.
Usually developing a large sphere of influence and enticing your opponent to invade it is a good strategy, because it creates a situation where you have numerical advantage and can attack severely.
In military texts, this is sometimes referred to as "force ratio".
The intention in Go though is not to kill, but to consolidate territory and gain advantages elsewhere while the opponent struggles to defend themselves.
Lee appeared to be off to a good start with this plan, pressuring White's invading group from all directions and forcing it to squirm uncomfortably.
But as the battle progressed, White gradually turned the tables — compounding small efficiencies here and there.
Lee seemed to be playing well, but somehow the computer was playing even better.
In forcing AlphaGo to withstand a very severe, one-sided attack, Lee revealed its hitherto undetected power.
Move after move was exchanged and it became apparent that Lee wasn't gaining enough profit from his attack.
By move 32, it was unclear who was attacking whom, and by 48 Lee was desperately fending off White's powerful counter-attack.
I can only speak for myself here, but as I watched the game unfold and the realization of what was happening dawned on me, I felt physically unwell.
Generally I avoid this sort of personal commentary, but this game was just so disquieting. I say this as someone who is quite interested in AI and who has been looking forward to the match since it was announced.
One of the game's greatest virtuosos of the middle game had just been upstaged in black and white clarity.
After losing the first three, Lee Sedol won his 4th game against the program AlphaGo!
Lee was playing white, which for go means taking the second move. So, he was on the defensive at first, unlike the previous game, where he played black.
After the first two hours of play, commenter Michael Redmond called the contest "a very dangerous fight". Lee Sedol likes aggressive play, and he seemed to be in a better position than last time.
But after another 20 minutes, Redmond felt that AlphaGo had the edge. Even worse, Lee Sedol had been taking a long time on his moves, so had only about 25 minutes left on his play clock, nearly an hour less than AlphaGo. Once your clock runs out, you need to make each move in less than a minute!
At this point, AlphaGo started to play less aggressively. Maybe it thought it was bound to win: it tries to maximize its probability of winning, so when it thinks it's winning it becomes more conservative. Commenter Chris Garlock said "This was AlphaGo saying: 'I think I'm ahead. I'm going to wrap this stuff up'. And Lee Sedol needs to do something special, even if it doesn't work. Otherwise, it's just not going to be enough".
On his 78th move, Lee did something startling.
He put a white stone directly between two of his opponent's stones, with no other white stone next to it. You can see it marked in red above. This is usually a weak type of move, since a stone that's surrounded is "dead".
I'm not good enough to understand precisely how strange this move was, or why it was actually good. At first all the commenters were baffled. And it seems to have confused AlphaGo. In the 87th move, AlphaGo placed a stone in a strange position which commentators said was "difficult to understand."
"AlphaGo yielded its own territory more while allowing its opponent to expand his own," said commentator Song Tae-gon, a Korean nine-dan professional go player. "This could be the starting point of AlphaGo's self-destruction."
Later AlphaGo placed a stone in the bottom left corner without reinforcing its territory in the center. Afterwards it seemed to recover, which Song said would be difficult for human players under such pressure. But Lee remained calm and blocked AlphaGo's attacks. The machine resigned on the 180th move.
Lee was ecstatic. "This win cannot be more joyful, because it came after three consecutive defeats. It is the single priceless win that I will not exchange for anything."
"AlphaGo seemed to feel more difficulties playing with black than white," he said. "It also revealed some kind of bug when it faced unexpected positions."
Lee has already lost the match, since AlphaGo won 3 out of the 5 games. But Lee wants to play black next time, and see if he can win that way.
You can play through the whole game here:
Well, if you look at the first hundred million primes, the answer is 25.000401%. That's very close to 1/4. And that makes sense, because there are just 4 digits that a prime can end in, unless it's really small: 1, 3, 7 and 9.
So, you might think the endings of prime numbers are random, or very close to it. But 3 days ago two mathematicians shocked the world with a paper that asked some other questions, like this:
I would have expected the answer to be close to 25%. But these mathematicians, Robert Oliver and Kannan Soundarajan, actually looked. And they found that among the first hundred million primes, the answer is just 17.757%.
So if a prime ends in a 7, it seems to somehow tell the next prime "I rather you wouldn't end in a 7. I just did that."
This initially struck me as weird. And apparently it's not just because I don't know enough number theory. Ken Ono is a real expert on number theory, and when he learned about this, he said:
I was floored. I thought, "For sure, your program's not working".
Needless to say, it's not magic. There is an explanation. In fact, Oliver and Soundarajan have conjectured a formula that says exactly how much of a discrepancy to expect — and they've checked it, and it seems to work. It works in every base, not just base ten. There's nothing special about base ten here. But we still need a proof that the formula really works.
By the way, their formula says the discrepancy gets smaller and smaller when we look at more and more primes. If we look at primes less than \(N\), the discrepancy is on the order of $$\frac{\log(\log(N))}{\log(N)} $$
This goes to zero as \(N \to \infty\). But this discrepancy is huge compared to the discrepancy for the simpler question, "what percentage of primes ends in a given digit?" For that, the discrepancy, called the Chebyshev bias, is on the order of $$ \frac{1}{\log(N) \sqrt{N}} $$
Of course, what's really surprising is not this huge correlation between the last digits of consecutive primes, but that number theorists hadn't thought to look for it until now!
Any amateur with decent programming skills could have spotted this and won everlasting fame, if they'd thought to look. What other patterns are hiding in the primes?
For a good nontechnical summary, read this:
I just noticed something funny. It seems that the Hardy–Littlewood \(k\)-tuple conjecture is also called the 'first Hardy–Littlewood conjecture'. The 'second Hardy–Littlewood conjecture' says that $$ \pi(M + N) \le \pi(M) + \pi(N) $$ whenever \(M,N \ge 2\), where \(\pi(N)\) is the number of primes \(\le N\).
What's funny is what Wikipedia says about the second Hardy–Littlewood conjecture! It says:
This is probably false in general as it is inconsistent with the more likely first Hardy–Littlewood conjecture on prime \(k\)-tuples, but the first violation is likely to occur for very large values of \(M\).Is this true? If so, did Hardy and Littlewood notice that their two conjectures contradicted each other? Isn't there some rule against this? Otherwise you could just conjecture \(P\) and also \(not(P)\), disguising \(not(P)\) in some very different language, and be sure that one of your conjectures was true!
(Unless, of course, you're an intuitionist.)
March 15, 2016

People love twin primes — primes separated by two, like 11 and 13. Nobody knows if there are infinitely many. There probably are. There are certainly lots.
But a while back, a computer search showed that among numbers less than a trillion, most common distance between successive primes is 6.
It seems that this trend goes on for quite a while longer.
... but in 1999, three mathematicians discovered that at some point, the number 6 ceases to be the most common gap between successive primes!
When does this change happen? It seems to happen around here: $$ 17,427,000,000,000,000,000,000,000,000,000 $$ At about this point, the most common gap between consecutive primes switches from 6 to 30.
They didn't prove this, but they gave a sophisticated heuristic argument for their claim. They also checked the basic idea using Maple's 'probable prime' function. It takes work to check if a number is prime, but there's a much faster way to check if it's probably prime in a certain sense. Using this, they worked out the gaps between probable primes from \(10^{30}\) and \(10^{30}+10^7\). They found that there are 5278 gaps of size 6 and just 5060 of size 30. They also worked out the gaps between probable primes from \(10^{40}\) and \(10^{40}+10^7\). There were 3120 of size 6 and 3209 of size 30.
So, it seems that somewhere between \(10^{30}\) and \(10^{40}\), the number 30 replaces 6 as the most probable gap between successive primes!
This is a nice example of how you may need to explore very large numbers to understand the true behavior of primes.
Using the same heuristic argument, they argued that somewhere around \(10^{450}\), the number 30 ceases to be the most probable gap. The number 210 replaces 30 as the champion — and reigns for an even longer time.
Furthermore, they argue that this pattern continues forever, with the main champions being the primorials: $$ 2 $$ $$ 2 \cdot 3 = 6 $$ $$ 2 \cdot 3 \cdot 5 = 30 $$ $$ 2 \cdot 3 \cdot 5 \cdot 7 = 210 $$ $$ 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2310 $$ etc.
Their paper is here:
The number $$ 2 \cdot 3 \cdot 5 \cdot 7 = 210 $$ starts becoming more common as a gap between primes than $$ 2 \cdot 3 \cdot 5 = 30$$ roughly when we reach $$\exp(2 \cdot 3 \cdot 5 \cdot 6 \cdot 5) = e^{900} \approx 10^{390} $$ Again, this is pretty rough: they must have a more accurate formula that they use elsewhere in the paper. But they mention this rough one early on.
I bet you still can't see the pattern in
that exponential, so let me do a couple more examples! The number
$$2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2310$$
starts becoming more common as a
gap between primes than
$$ 2 \cdot 3 \cdot 5 \cdot 7 = 210 $$
roughly when we reach
$$ \exp(2 \cdot 3 \cdot 5 \cdot 7 \cdot 10 \cdot 9) = e^{18900} $$
The number
$$ 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 = 30030 $$
starts becoming more common as a gap between primes than
$$ 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2310 $$
roughly when we reach
$$ \exp(2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 12 \cdot 11) = e^{304920} $$
Get the pattern? If not, read their paper.
March 16, 2016
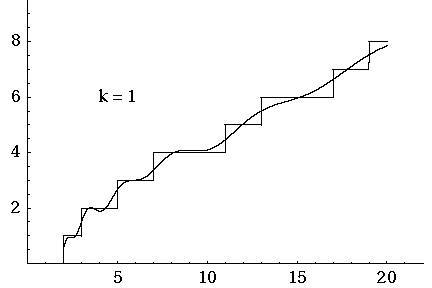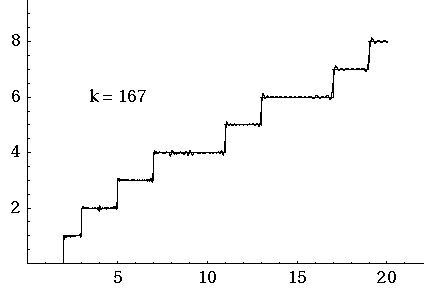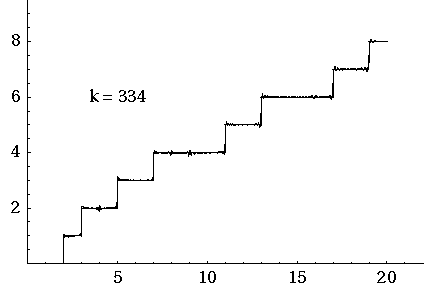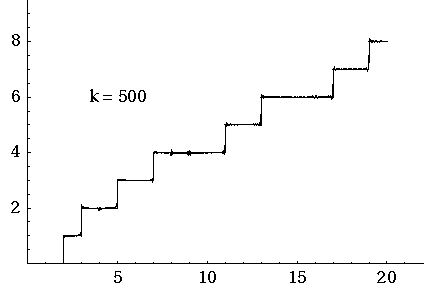
I often hear there's no formula for prime numbers. But Riemann came up with something just as good: a formula for the prime counting function.
This function, called \(\pi(x)\), counts how many prime numbers there are less than \(x\), where \(x\) is any number you want. It keeps climbing like a staircase, and it has a step at each prime. You can see it above.
Riemann's formula is complicated, but it lets us compute the prime counting function using a sum of oscillating functions. These functions oscillate at different frequencies. Poetically, you could say they reveal the secret music of the primes.
The frequencies of these oscillating functions depend on where the Riemann zeta function equals zero.
So, Riemann's formula turns the problem of counting primes less than some number into another problem: finding the zeros of the Riemann zeta function!
This doesn't make the problem easier... but, it unlocks a whole new battery of tricks for understanding prime numbers! Many of the amazing things we now understand about primes are based on Riemann's idea.
It also opens up new puzzles, like the Riemann Hypothesis: a guess about where the Riemann zeta function can be zero. If someone could prove this, we'd know a lot more about prime numbers!
The animated gif here shows how the prime counting function is approximated by adding up oscillating functions, one for each of the first 500 zeros of the Riemann zeta function. So when you see something like "k = 317", you're getting an approximation that uses the first 317 zeros.
Here's a view of these approximations of the prime counting function \(\pi(x)\) between \(x = 190\) and \(x = 230\):
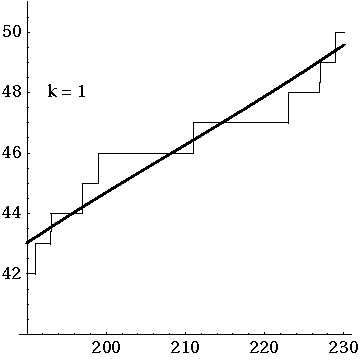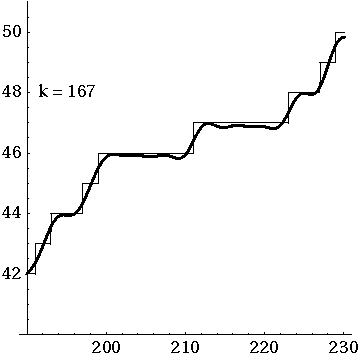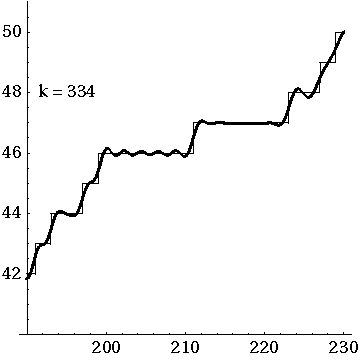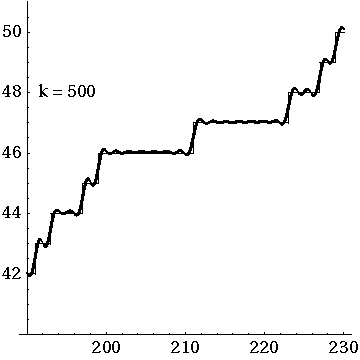
I got these gifs here:
and here you can see Riemann's formula. You'll see that some other functions, related to the prime counting function, have simpler formulas.
And by the way: when I'm talking about zeros of the Riemann zeta function, I only mean zeros in the critical strip, where the real part is between 0 and 1. The Riemann Hypothesis says that for all of these, the real part is exactly 1/2. This has been checked for the first 10,000,000,000,000 zeros.
That sounds pretty convincing, but it shouldn't be. After all, the number 6 is the most common gap between consecutive primes if we look at numbers less than something like 17,427,000,000,000,000,000,000,000,000,000... but then that pattern stops!
So, you shouldn't look at a measly few examples and jump to big conclusions when it comes to primes.
March 17, 2016
Greg Bernhardt runs a website called for discussing physics, math and
other topics. He recently did a two-part interview of me, and you can
see it there
or all in
one place on my website.
March 18, 2016

Here's how you figure it out. \(i\) is e to the power of \(i \pi/2\), since multiplying by \(i\) implements a quarter turn rotation, that is, a rotation by \(\pi/2\). So, $$ i^{\, i} = (e^{i \pi/2})^i = e^{i \cdot i\pi/2} = e^{-\pi/2} = 0.20787957... $$ Sorta strange. But now:
Puzzle. Can you solve the equation on the album cover for \(\heartsuit\)? $$ i^{\, i} = \heartsuit^{{}^{\sqrt{- \frac{\heartsuit}{2}}}} $$ If you get stuck, see Greg Egan's answer in the comments to my Google+ post. But my real puzzle is about the album cover this equation appears on!
Is there any way to get a good electronic copy of this album for less than $50? There's one CD of it for sale on Amazon for $50.
It's called This Crazy Paradise and it's by Pyewackett. It's a cool album! It was made in 1986. It's an unusual blend of the cutting-edge electronic rock of that day and traditional folk music. The singer, Rosie Cross, has a voice that reminds me of Maddy Prior of Steeleye Span.
When it first came out I liked the electronic aspects, but not the folk. Now I like both — and it bothers me that this unique album seems almost lost to the world!
My wife Lisa has a tape of it. She transferred the tape to mp3 using Audacity but the result was fairly bad... a lot of distortion. Part of the problem ws a bad cassette tape deck — I've got a much better one, and I should try it. But I'm afraid another part of the problem is that without a special sound card, using the 'line in' on your laptop produces crappy recordings. I'll see.
Here's a description of the band from Last.fm:
The English folkrock group Pyewackett was founded at the end of the 1970s by Ian Blake and Bill Martin. They were a resident band and the London University college folk club.Here's a review by Craig Harris:Pyewackett played traditional folk music by the motto "pop music from the last five centuries": 15th century Italian dances, a capella harmonies, traditional songs in systems/minimalist settings, 1920's ballads, etc.. The distinctive sound was characterised by the unusual combination of woodwinds, strings and keyboards. The voices were also a strong trademark. All these features of the Pyewackett sound are shown best on the second album the band released in 1984, The Man in the Moon Drinks Claret. It is this album that has been re-released in Music & Words. Folk Classics series. At the time of this recording the band was formed by Ian Blake, Bill Martin, Mark Emerson, Rosie Cross and guest drummer Micky Barker. The album has been co-produced by Andrew Cronshaw.
One of the lesser-known of the British folk bands, Pyewackett is remembered for updating 18th century songs with modern harmonies and inventive instrumentation. While none of their four albums are easy to find, the search is worth it. The group's sense of fun and reverence for musical traditions allowed them to bring ancient tunes to life. Pyewackett took their name from an imp that a 17th century Essex woman claimed possessed her. According to legendary witch-hunter Matthew Hopkins, it was a name that "no mortal could invent."If you want to hear a bit of Pyewackett, try this:
It's less electronic, but still a good bass line spices up this rendition of the traditional "Tam Lin". For the lyrics, see this:
[...] a character in a legendary ballad originating from the Scottish Borders. It is also associated with a reel of the same name, also known as Glasgow Reel. The story revolves around the rescue of Tam Lin by his true love from the Queen of the Fairies. While this ballad is specific to Scotland, the motif of capturing a person by holding him through all forms of transformation is found throughout Europe in folktales. The story has been adapted into various stories, songs and films.
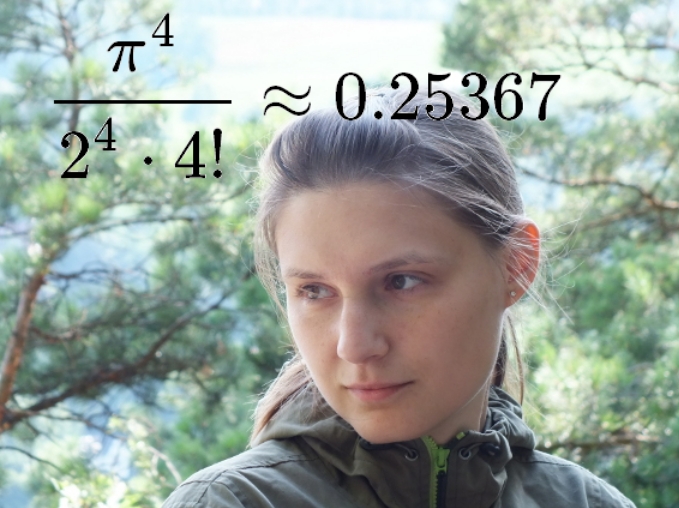
Ten days ago, the Ukranian mathematician Maryna Viazovska showed how to pack spheres in 8 dimensions as tightly as possible. In this arrangement the spheres occupy about 25.367% of the space. That looks like a strange number — but it's actually a wonderful number, as shown here.
People had guessed the answer to this problem for a long time. If you try to get as many equal-sized spheres to touch a sphere in 8 dimensions, there's exactly one way to do it — unlike in 3 dimensions, where there's a lot of wiggle room! And if you keep doing this, on and on, you're forced into a unique arrangement, called the \(\mathrm{E}_8\) lattice. So this pattern is an obvious candidate for the densest sphere packing in 8 dimensions. But none of this proves it's the best!
In 2001, Henry Cohn and Noam Elkies showed that no sphere packing in 8 dimensions could be more than 1.000001 times as dense than \(\mathrm{E}_8\). Close... but no cigar.
Now Maryna Viazovska has used the same technique, but pushed it further. Now we know: nothing can beat \(\mathrm{E}_8\) in 8 dimensions!
Viazovska is an expert on the math of modular forms, and that's what she used to crack this problem. But when she's not working on modular forms, she writes papers on physics! Serious stuff, like "Symmetry and disorder of the vitreous vortex lattice in an overdoped BaFe2-xCox As2 superconductor."
After coming up with her new ideas, Viaskovska teamed up with other experts including Henry Cohn and proved that another lattice, the Leech lattice, gives the densest sphere packing in 24 dimensions.
Different dimensions have very different personalities. Dimensions 8 and 24 are special. You may have heard that string theory works best in 10 and 26 dimensions — two more than 8 and 24. That's not a coincidence.
The densest sphere packings of spheres are only known in dimensions 0, 1, 2, 3, and now 8 and 24. Good candidates are known in many other low dimensions: the problem is proving things — and in particular, ruling out the huge unruly mob of non-lattice packings.
For example, in 3 dimensions there are uncountably many non-periodic packings of spheres that are just as dense as the densest lattice packing!
In fact, the sphere packing problem is harder in 3 dimensions than 8. It was only solved earlier because it was more famous, and one man — Thomas Hales — had the nearly insane persistence required to crack it.
His original proof was 250 pages long, together with 3 gigabytes of computer programs, data and results. He subsequently verified it using a computerized proof assistant, in a project that required 12 years and many people.
By contrast, Viazovska's proof is extremely elegant. It boils down to finding a function whose Fourier transform has a simple and surprising property! For details on that, try my blog article: