

It came as a shock because it's a brand-new Johnson solid — a convex polyhedron whose faces are all regular polygons.
Johnson solids are named after Norman Johnson, who in 1966 published a list of 92 such solids. He conjectured that this list was complete, but did not prove it.
In 1969, Victor Zalgaller proved that Johnson's list was complete, using the fact that there are only 92 elements in the periodic table.
It thus came as a huge shock to the mathematical community when Craig Kaplan, a computer scientist at the University of Waterloo, discovered an additional Johnson solid!
At the time, he was compiling a collection of 'near misses': polyhedra that come very close to being Johnson solids. In an interview with the New York Times, he said:
When I found this one, I was impressed at how close it came to being a Johnson solid. But then I did some calculations, and I was utterly flabbergasted to discover that the faces are exactly regular! I don.t know how people overlooked it.
It turned out there was a subtle error in Zalgaller's lengthy proof.
Or maybe not; for details see:
As you know, a lot of conservatives in the US support the right to bear arms. It's in the Bill of Rights, after all:
"A well regulated militia being necessary to the security of a free state, the right of the people to keep and bear arms shall not be infringed."The idea is basically that if enough of us good guys are armed, criminals and the government won't dare mess with us.
In this they are in complete agreement with the Black Panthers, a revolutionary black separatist organization founded in the 1960s by Huey P. Newton. Later it became less active, but in 1989 the New Black Panther Party was formed in South Dallas, a predominantly black part of Dallas, Texas. They helped set up the Huey P. Long Gun Club, "uniting five local black and brown paramilitary organizations under a single banner."
Above you see some of their members marching in a perfectly legal manner down the streets of South Dallas. They started doing this after the killing of Michael Brown by a policeman in Ferguson.
On a warm fall day in South Dallas, ten revolutionaries dressed in kaffiyehs and ski masks jog the perimeter of Dr. Martin Luther King Jr. Park bellowing "No more pigs in our community!" Military discipline is in full effect as the joggers respond to two former Army Rangers in desert-camo brimmed hats with cries of "Sir, yes, sir!" The Huey P. Newton Gun Club is holding its regular Saturday fitness-training and self-defense class. Men in Che fatigues run with weight bags and roll around on the grass, knife-fighting one another with dull machetes." I used to salute the fucking flag!" the cadets chant. "Now I use it for a rag!"You'd think that white conservatives would applaud this "well-regulated militia", since they too are suspicious of the powers of the government. Unfortunately they have some differences of opinion.
For one thing, there's that white versus black business, and the right-wing versus left-wing business. To add to the friction, the Black Panthers are connected to the Nation of Islam, a black Muslim group, while the white conservatives tend to be Christian.
It was thus not completely surprising when a gun-toting right-wing group decided to visit a Nation of Islam mosque in South Dallas. This group has an amusingly bland name: The Bureau of American Islamic Relations. They wrote:
We cannot stand by while all these different Anti American, Arab radical Islamists team up with Nation of Islam/Black Panthers and White anti American Anarchist groups, joining together in the goal of destroying our Country and killing innocent people to gain Dominance through fear!
So, yesterday, the so-called Bureau showed up at the Nation of Islam mosque in South Dallas. They were openly carrying guns.
But the Huey P. Newton Gun Club expected this. So they showed up in larger numbers, carrying more guns.
Things became tense. People stood around holding guns, holding signs, yelling at each other, exercising all their constitutional freedoms like good Americans: the right of free speech, the right of assembly, the right to bear arms.
In the end, no shots were fired. The outgunned Bureau went home.
One of the co-founders of the Huey P. Newton Gun Club was interviewed while this was going on. He said:
Those banditos are out of their minds if they think they're going to come to South Dallas like this.See? This is how the 2nd Amendment works.
For more, see:
Last month the logician Joel David Hamkins proved a surprising result: you can compute uncomputable functions!
Of course there's a catch, but it's still interesting.
Alan Turing showed that a simple kind of computer, now called a Turing machine, can calculate a lot of functions. In fact we believe Turing machines can calculate anything you can calculate with any fancier sort of computer. So we say a function is computable if you can calculate it with some Turing machine.
Some functions are computable, others aren't. That's a fundamental fact.
But there's a loophole.
We think we know what the natural numbers are:
and how to add and multiply them. We know a bunch of axioms that describe this sort of arithmetic: the Peano axioms. But these axioms don't completely capture our intuitions! There are facts about natural numbers that most mathematicians would agree are true, but can't be proved from the Peano axioms.
Besides the natural numbers you think you know — but do you really? — there are lots of other models of arithmetic. They all obey the Peano axioms, but they're different. Whenever there's a question you can't settle using the Peano axioms, it's true in some model of arithmetic and false in some other model.
There's no way to decide which model of arithmetic is the right one — the so-called 'standard' natural numbers.
Hamkins showed there's a Turing machine that does something amazing. It can compute any function from the natural numbers to the natural numbers, depending on which model of arithmetic we use.
In particular, it can compute the uncomputable... but only in some weird 'alternative universe' where the natural numbers aren't what we think they are.
These other universes have 'nonstandard' natural numbers that are bigger than the ones you understand. A Turing machine can compute an uncomputable function... but it takes a nonstandard number of steps to do so.
So: computing the computable takes a 'standard' number of steps. Computing the uncomputable takes a little longer.
This is not a practical result. But it shows how strange simple things like logic and the natural numbers really are.
For a better explanation, read my blog post:
And for the actual proof, go on from there to the blog article by Joel
David Hamkins.
April 12, 2016

Carbon can form diamonds, and the geometry of the diamond crystal is amazingly beautiful. But there's another crystal, called the 'triamond', that is just as beautiful. It was discovered by mathematicians, but it doesn't seem to exist in nature.
In a triamond, each carbon atom would be bonded to three others at 120° angles, with one double bond and two single bonds. Its bonds lie in a plane, so we get a plane for each atom.
But here's the tricky part: for any two neighboring atoms, these planes are different. And if we draw these bond planes for all the atoms in the triamond, they come in four kinds, parallel to the faces of a regular tetrahedron!
The triamond is extremely symmetrical. But it comes in left- and right-handed forms, unlike a diamond.
In a diamond, the smallest rings of carbon atoms have 6 atoms. A rather surprising thing about the triamond is that the smallest rings have 10 atoms! Each atom lies in 15 of these 10-sided rings.
When I heard about the triamond, I had to figure out how it works. So I wrote this:
The thing that got me excited in the first place was a description of the 'triamond graph' — the graph with carbon atoms as vertices and bonds as edges. It's a covering space of the complete graph with 4 vertices. It's not the universal cover, but it's the 'universal abelian cover'.
I guess you need to know a fair amount of math to find that exciting. But fear not — I lead up to this slowly: it's just a terse way to say a lot of fun stuff.
And while the triamond isn't found in nature (yet), the
mathematical pattern of the triamond is found in some butterfly wings.
April 14, 2016

In math there are infinite numbers called cardinals, which say how big sets are. Some are small. Some are big. Some are infinite. Some are so infinitely big that they're inaccessible — very roughly, you can't reach them using operations you can define in terms of smaller cardinals.
An inaccessible cardinal is so big that if it exists, we can't prove that using the standard axioms of set theory!
The reason why is pretty interesting. Assume there's an inaccessible cardinal \(\kappa\). If we restrict attention to sets that we can build up using fewer than \(\kappa\) operations, we get a whole lot of sets. Indeed, we get a set of sets that does not contain every set, but which is big enough that it's 'just as good' for all practical purposes.
We call such a set a Grothendieck universe. It's not the universe — we reserve that name for the collection of all sets, which is too big to be a set. But all the usual axioms of set theory apply if we restrict attention to sets in a Grothendieck universe.
In fact, if we assume that an inaccessible cardinal exists, we can use the resulting Grothendieck universe to prove that the usual axioms of set theory are consistent! The reason is that the Grothendieck universe gives a 'model' of the axioms — it obeys the axioms, so the axioms must be consistent.
However, Gödel's first incompleteness theorem says we can't use the axioms of set theory to prove themselves consistent... unless they're inconsistent, in which case all bets are off.
The upshot is that we probably can't use the usual axioms of set theory to prove that it's consistent to assume there's an inaccessible cardinal. If we could, set theory would be inconsistent!
Nonetheless, bold set theorists are fascinated by inaccessible cardinals, and even much bigger cardinals. For starters, they love the infinite and its mysteries. But also, if we assume these huge infinities exist, we can prove things about arithmetic that we can't prove using the standard axioms of set theory!
I gave a very rough definition of inaccessible cardinals. It's not hard to be precise. A cardinal \(\kappa\) is inaccessible if you can't write it as a sum of fewer than \(\kappa\) cardinals that are all less than \(\kappa\), and if \(\alpha\) is any cardinal less than \(\kappa\), then \(2^\alpha\) is also less than \(\kappa\).
Well, not quite. According to this definition, 0 would be
inaccessible — and so would the very
smallest infinite cardinal, \(\aleph_0\). Neither of these can be
reached 'from below'. But we don't count these two cardinals as
inaccessible.
April 23, 2016

Math tells us three of the saddest love stories:
The Barth sextic is an amazing surface with 65 points that look like the place where two cones meet — the most possible for a surface described using polynomials of degree 6. But in the usual picture of this surface, which emphasizes its symmetry, 15 of these points lie at infinity.
In this picture by Abdelaziz Nait Merzouk, the Barth sextic has been rotated to bring some of these points into view! It's also been sliced so you can see inside.
You can learn more about the Barth sextic here:
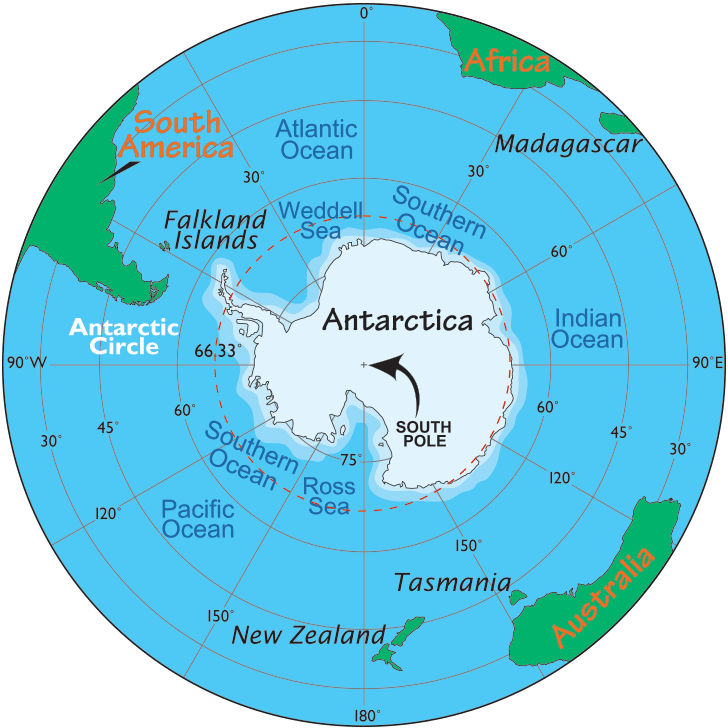
There are lots of flights that go near the North Pole. When you fly from California to Europe, for example, that's an efficient route! Are there flights that go near the South Pole? If not, why not?
A friend of mine asked this question, and I promised I'd try to get an answer. When she flew from Argentina to New Zealand she took a very long route. Why, she wondered, don't airplanes take a southerly route? Is the weather too bad?
My guess is that maybe there's not enough demand to fly from South America to New Zealand for there to be direct flights. Or from South America to South Africa, or Madagascar.
But I haven't even checked! Maybe there are such flights!
April 30, 2016
On January 18, 2000, at 8:43 in the morning, a meteor hit the Earth's atmosphere over Canada and exploded with the energy of a 1.7 kiloton bomb. Luckily this happened over a sparsely populated part of British Columbia.
It was over 50 tons in mass when it hit the air, but 97% of it vaporized. Just about a ton reached the Earth. It landed on Tagish Lake, which was frozen at the time. Local inhabitants said the air smelled like sulfur.
Only about 10 kilograms was found and collected. Except for a gray crust, the pieces look like charcoal briquettes.
And here is where things get interesting.
Analysis of the Tagish Lake fragments show they're very primitive. They contain dust granules that may be from the original cloud of material that created our Solar System and Sun! They also have a lot of of organic chemicals, including amino acids.
It seems this rock was formed about 4.55 billion years ago.
Scientists tried to figure out where it came from. They reconstructed its direction of motion and compared its properties with the spectra of various asteroids. In the end, they guessed that it most likely came from 773 Irmintraud.
773 Irmintraud is a dark, reddish asteroid from the outer region of the asteroid belt. It's about 92 kilometers in diameter. It's just 0.034 AU away from a chaotic zone associated with one of the gaps in the asteroid belt created by a resonance with Jupiter. So, if a chunk got knocked off, it could wind up moving chaotically and make it to Earth!
And here's what really intrigues me. 773 Irmintraud is a D-type asteroid — a very dark and rather rare sort. One model of Solar System formation says these asteroids got dragged in from very far out in the Solar System: the Kuiper Belt, out beyond Pluto. (Some scientists think Mars' moon Phobos is also a D-type asteroid.)
So, this chunk of rock here may have been made out in the Kuiper Belt, over 4.5 billion years ago!
For more, see: