A sea otter and her sleeping pup float downstream.
For the whole adorable video, taken by Connie Levenhagen in the 'Great
Tide Pool' at the Monterey Bay Aquarium,
see YouTube.
May 2, 2016
David Broadhurst is a particle physicist at Open University who is famous for his calculations of complicated Feynman diagrams revealing fascinating connections to number theory. Open University, in England, is the world's first successful distance learning university. They used to give courses on TV and radio. Maybe they still do, but now the internet is the big thing.
Today David Broadhurst emailed me a link to this old announcement. As you can see here, my uncle Albert Baez was a visiting professor at Open Universsity and gave a physics lecture there. I like this quick philosophy of science:
At the end Professor Baez summarises what characterises a scientist: longing to know and understand; questioning; searching for meaningful relations; demand for verification and respect for logic.

It's fun to read the frequently asked questions on the Flat Earth Society wiki. First question:
Is this site a joke?
Answer: no, we're just diagonally parked in a parallel universe.
Sorry — that's my answer, not theirs. This site claims not to be a joke. But it's sure funny.
How do you explain day/night cycles and seasons?Day and night cycles are easily explained on a flat earth. The sun moves in circles around the North Pole. When it is over your head, it's day. When it's not, it's night. The sun acts like a spotlight and shines downward as it moves. The picture below illustrates how the sun moves and also how seasons work on a flat earth. The apparent effect of the sun rising and setting is usually explained as a perspective effect.
And all that stuff about the Moon's phases, and lunar and solar eclipses, was apparently set up just to fool us into thinking the Earth, Moon and Sun are round objects, with the Earth able to come between the Sun and Moon, and the Moon able to come between the Earth and Sun.
But what I really like is the explanation of gravity. Wouldn't gravity pull the Earth into a round ball? No:
The earth is constantly accelerating up at a rate of 32 feet per second squared (or 9.8 meters per second squared). This constant acceleration causes what you think of as gravity. Imagine sitting in a car that never stops speeding up. You will be forever pushed into your seat.
That's brilliant! But wait a minute...
Objects cannot exceed the speed of light. Doesn't this mean that the Earth can't accelerate forever?
They've got an answer to that too:
Due to special relativity, this is not the case. At this point, many readers will question the validity of any answer which uses advanced, intimidating-sounding physics terms to explain a position. However, it is true. The velocity can never reach the speed of light, regardless of how long one accelerates for and the rate of the acceleration.
Fantastic!
What I like about this is that people can understand special relativity, yet not believe the Earth is round. I had never encountered that combination. I know more people who go the other way.
Of course there's the problem of what's powering this eternal acceleration. But they have an answer to that too: it's the Universal Accelerator, also known as dark energy or the "aetheric wind".
Here's the site:
Puzzle. Assume the Earth is 6000 years old and has been accelerating at 9.8 meters per second per second throughout this time, as measured in its own instantaneous rest frame. If it started at rest, how fast is it going now? Use the formula for Lorentz contractions to compute the thickness of the Earth today as measured by an observer at rest.
I'd guess it's much thinner than the diameter of a proton!
Some hints for anyone who has a calculator and is willing to use it:
If an object has constant acceleration \(a\) in its own rest frame and starts at rest, after time \(t\) its velocity will be $$ v = c \tanh(at/c) $$ where \(c\) is the speed of light and \(\tanh\) is the hyperbolic tangent function. Also, if an object is moving at a velocity \(v\), the Lorentz contraction will multiply its thickness by $$ 1/\sqrt{1-v^2/c^2} $$ On the long discussion about this flat Earth theory on G+, Asbjørn Held provided the following answer:
As they say, go big or go home... I used Boost's Multiprecision library to compute the inverse gamma factor with 10000 decimal digits precision (maybe I could have used less, but 1000 was not enough). This was assuming the earth was 6000 years.The thickness of the earth relative to an observer at rest would be about \(3.69 \times 10^{-2684}\) meters... I'd consider that flat!

For the record, at that speed \(\beta\) (that is \(v/c\), the fraction of speed of light) equals
0.999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 99999999999999999999999999999999999999999999999999999999999999999999 999999999995816429156...Just in case I made some errors, here's the code.
I had tried this computation myself but I soon realized that the Earth would be very flattened after accelerating at 1 gee for 6000 years.
I believe its speed would be
$$ \tanh(\mathrm{year}/\mathrm{second} \times 6000 \; \mathrm{year} \times 9.8\; \mathrm{meter}/\mathrm{second}^2 / c) = $$
$$ \tanh(31536000 \times 6000 \times 9.8 / 299792458) \approx $$
$$ \tanh(6185.33505603) \approx $$
$$ 1 - 2 \exp(-2 \times 6185.33505603) \approx $$
$$ 1 - 2 \exp(-12370.6701121) $$
times the speed of light. In short: absurdly close to the speed of light!
So, yes, it will be very flattened.
May 12, 2016
Kevin Kelly has claimed that "tools never die": that any tool ever made is still being made somewhere. There are interesting arguments about this online. You can find videos on how to make stone hand axes. You can find instructions on how make a calcium oxide light — the old-fashioned 'limelight' used in theaters until it was replaced by electric arc lamp in the 1890s.
And you can certainly buy a longsword. That's a sword with a long double-edged blade and a cross-shaped handle, as shown here. They reached their height of popularity from 1350 to 1550. But people still fight with them — mainly for fun.
In fact, this weekend on Staten Island there's a course for women who want to fight with longswords! And there's a tournament, too! It's called Fecht Yeah. Bring our weapon.
It's part of the Historical European Martial Arts movement, or HEMA. Here's the ad:
A weekend of training, learning, and collaboration for women who study HEMA and other sword arts.I'm an absurdly nonviolent guy, who will pick up a spider and take it outside rather than squash it. But I admire skills like sword-fighting, and I'm glad people are keeping those skills alive. Why? I'm not completely sure. I could theorize about it, but never mind.This is an event for women of all skill levels with varied interests to come together and develop their skills. Workshops for beginners will be available. Free from tournament pressure and the constraints of classes, we have the ability to workshop teaching methods, rulesets, and learning strategies with other dedicated practitioners.
We will have laurel tournaments in longsword, sword and buckler, rapier, and saber. Prizes will be modest. Attend to learn, not win.
Check out this video of German longsword fighting:
As you might expect, female swordfighters get flack from some male ones. There's a nice article about Fecht Yeah here, and it gets into that a bit:
The woman in the picture above is Laura McBride, photographed by Brad Trent. Tiby Kantorowitz, one of the women running Fecht Yeah, treats swordfighting as a spiritual exercise:
It's the flip side to yoga. It's easy to Zen out with twinkly music, incense, and soft light. But can I maintain the same equanimity when there's some six-foot guy" — she's four-ten — "with a sword who's trying to brain me?"
For Kevin Kelly's claim, try this:
Krulwich: And then he made this ridiculous bet. He said: I bet you can't find any tool, any machine — go back to any century you like — that still isn't being made and made new today. So all I have to do is find a single tool that's not being made anymore, and I win.And then the show explores this...(Soundbite of laughter)
Kelly: Yes, that's right.
Krulwich: You're so going to lose this.
The Earth is heating up rapidly. This great image was made by Ed Hawkins, a climate scientist at the University of Reading in the United Kingdom.
He points out some features:
1877-78: strong El Niño event warms global temperaturesHe used temperature data from January 1850 to March 2016. The numbers give the temperature above the average of 1850-1900. The temperatures are from a British data set called HadCRUT4.4. You can get that data here:1880s-1910: small cooling, partially due to volcanic eruptions
1910-1940s: warming, partially due to recovery from volcanic eruptions, small increase in solar ouput and natural variability
1950s-1970s: fairly flat temperatures as cooling sulphate aerosols mask the greenhouse gas warming
1980-now: strong warming, with temperatures pushed higher in 1998 and 2016 due to strong El Niño events
and Hawkin's blog:

This is Danny MacAskill on the Inaccessible Pinnacle on the Isle of Skye.
He is a great mountain biker, but he had to carry the bike up the last part of this scary peak.
The Isle of Skye is an island off the west coast of Scotland. It's the largest of the Inner Hebrides, and the most northerly of the large islands in this group. In the center of this island is a mountain range called the Cuillin, and the Inaccessible Pinnacle sits among these.
Skye has been occupied since Mesolithic times, and it appears in Norse poetry, for example in this romantic line:
Almost a third of the inhabitants still speak Gaelic, and apart from a few bigger towns, the population lives in crofting townships scattered around the coastline. "Crofting"? Yeah, a croft is a small farm with a wall around it.
The only distillery on the Isle of Skye is the Talisker Distillery, which makes a rather famous single malt Scotch whisky. It's in a village on the south shore.
I've always been fascinated by the Inner Hebrides and the even more exotic-sounding Outer Hebrides. I'm annoyed at how all my visits to the British Isles have only taken me to the lofty centers of academe, not places like this. I don't know much about them, but anything remote appeals to me: inaccessible pinnacles, inaccessible cardinals, the Taklamakan desert, the underground oceans of Europa....
Danny MacAskill is actually from the Isle of Skye! You can see his whole journey along the Cuillin Ridgeline here:
Pretty impressive! Beautiful scenery, too!
May 24, 2016
This month, a bunch of 'logic hackers' have stepped up to the plate and made a lot of progress. They've sharpened our estimate of where this boundary lies. How? By writing shorter and shorter computer programs for which it's unknowable whether these programs run forever, or stop.
A 'Turing machine' is a simple kind of computer whose inner workings have N different states, for some number N = 1,2,3,...
The 'Busy Beaver Game' is to look for the Turing machine with N states that runs as long as possible before stopping. Machines that never stop are not allowed in this game.
We know the winner of the Busy Beaver Game for N = 1,2,3 and 4. Already for N = 5, the winner is unknown. The best known contestant is a machine that runs for 47,176,870 steps before stopping. There are 43 machines that might or might not stop — we don't know.
When N is large enough, the winner of the Busy Beaver Game is unknowable.
More precisely, if you use the ordinary axioms of mathematics, it's impossible to prove that any particular machine with N states is the winner of the Busy Beaver Game... as long as those axioms are consistent.
How big must N be, before we hit this wall?
We don't know.
But earlier this month, Adam Yedidia and Scott Aaronson showed that it's 7910 or less.
And by now, thanks to a group of logic hackers like Stefan O'Rear, we know it's 1919 or less.
So, the unknowable kicks in — the winner of the Busy Beaver Game for N-state Turing machines becomes unknowable using ordinary math - somewhere between N = 5 and N = 1919.
The story of how we got here is is fascinating, and you can read about it on my blog post:
Anything that I didn't make clear here, should be explained there.
May 27, 2016
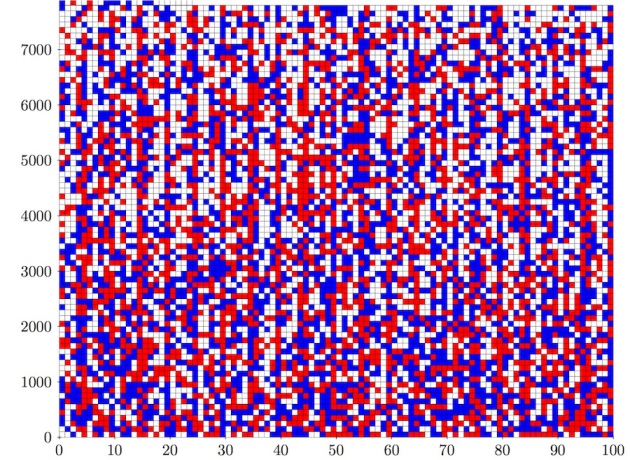
In the 1980s, the mathematician Ronald Graham asked if it's possible to color each positive integer either red or blue, so that no triple of integers \(a, b\) and \(c\) obeying Pythagoras' famous equation:
all have the same color. He offered a prize of $100.
Now it's been solved! The answer is no. You can do it for numbers up to 7824, and a solution is shown in this picture. But you can't do it for numbers up to 7825.
To prove this, you could try all the ways of coloring these numbers and show that nothing works. Unfortunately that would require trying
3 628 407 622 680 653 855 043 364 707 128 616 108 257 615 873 380 491 654 672 530 751 098 578 199 115 261 452 571 373 352 277 580 182 512 704 196 704 700 964 418 214 007 274 963 650 268 320 833 348 358 055 727 804 748 748 967 798 143 944 388 089 113 386 055 677 702 185 975 201 206 538 492 976 737 189 116 792 750 750 283 863 541 981 894 609 646 155 018 176 099 812 920 819 928 564 304 241 881 419 294 737 371 051 103 347 331 571 936 595 489 437 811 657 956 513 586 177 418 898 046 973 204 724 260 409 472 142 274 035 658 308 994 441 030 207 341 876 595 402 406 132 471 499 889 421 272 469 466 743 202 089 120 267 254 720 539 682 163 304 267 299 158 378 822 985 523 936 240 090 542 261 895 398 063 218 866 065 556 920 106 107 895 261 677 168 544 299 103 259 221 237 129 781 775 846 127 529 160 382 322 984 799 874 720 389 723 262 131 960 763 480 055 015 082 441 821 085 319 372 482 391 253 730 679 304 024 117 656 777 104 250 811 316 994 036 885 016 048 251 200 639 797 871 184 847 323 365 327 890 924 193 402 500 160 273 667 451 747 479 728 733 677 070 215 164 678 820 411 258 921 014 893 185 210 250 670 250 411 512 184 115 164 962 089 724 089 514 186 480 233 860 912 060 039 568 930 065 326 456 428 286 693 446 250 498 886 166 303 662 106 974 996 363 841 314 102 740 092 468 317 856 149 533 746 611 128 406 657 663 556 901 416 145 644 927 496 655 933 158 468 143 482 484 006 372 447 906 612 292 829 541 260 496 970 290 197 465 492 579 693 769 880 105 128 657 628 937 735 039 288 299 048 235 836 690 797 324 513 502 829 134 531 163 352 342 497 313 541 253 617 660 116 325 236 428 177 219 201 276 485 618 928 152 536 082 354 773 892 775 152 956 930 865 700 141 446 169 861 011 718 781 238 307 958 494 122 828 500 438 409 758 341 331 326 359 243 206 743 136 842 911 727 359 310 997 123 441 791 745 020 539 221 575 643 687 646 417 117 456 946 996 365 628 976 457 655 208 423 130 822 936 961 822 716 117 367 694 165 267 852 307 626 092 080 279 836 122 376 918 659 101 107 919 099 514 855 113 769 846 184 593 342 248 535 927 407 152 514 690 465 246 338 232 121 308 958 440 135 194 441 048 499 639 516 303 692 332 532 864 631 075 547 542 841 539 848 320 583 307 785 982 596 093 517 564 724 398 774 449 380 877 817 714 717 298 596 139 689 573 570 820 356 836 562 548 742 103 826 628 952 649 445 195 215 299 968 571 218 175 989 131 452 226 726 280 771 962 970 811 426 993 797 429 280 745 007 389 078 784 134 703 325 573 686 508 850 839 302 112 856 558 329 106 490 855 990 906 295 808 952 377 118 908 425 653 871 786 066 073 831 252 442 345 238 678 271 662 351 535 236 004 206 289 778 489 301 259 384 752 840 495 042 455 478 916 057 156 112 873 606 371 350 264 102 687 648 074 992 121 706 972 612 854 704 154 657 041 404 145 923 642 777 084 367 960 280 878 796 437 947 008 894 044 010 821 287 362 106 232 574 741 311 032 906 880 293 520 619 953 280 544 651 789 897 413 312 253 724 012 410 831 696 803 510 617 000 147 747 294 278 502 175 823 823 024 255 652 077 422 574 922 776 413 427 073 317 197 412 284 579 070 292 042 084 295 513 948 442 461 828 389 757 279 712 121 164 692 705 105 851 647 684 562 196 098 398 773 163 469 604 125 793 092 370 432possibilities. But recently, three mathematicians cleverly figured out how to eliminate most of the options. That left fewer than a trillion to check!
So they spent 2 days on a supercomputer, running 800 processors in parallel, and checked all the options. None worked. They verified their solution on another computer.
This is the world's biggest proof: it's 200 terabytes long! That's about equal to all the digitized text held by the US Library of Congress. There's also a 68-gigabyte digital signature - sort of a proof that a proof exists - if you want to skim it.
It's interesting that these 200 terabytes were used to solve a yes-or-no question, whose answer takes a single bit to state: no.
I'm not sure breaking the world's record for the longest proof is something to be proud of. Mathematicians prize short, elegant proofs. I bet a shorter proof of this result will eventually be found.
Still, it's fun that we can do such things. Here's a story about the proof:
The 'cube-and-conquer' paradigm is a "hybrid SAT method for hard problems, employing both look-ahead and CDCL solvers"... whatever that means. It would be interesting to learn about this. But it's time for breakfast!
By the way, despite the title of the Nature article, in the comments to my G+ post about this, Michael Nielsen pointed out a longer proof by Chris Jefferson, who wrote:
Darn, I had no idea one could get into the media with this kind of stuff.His team found a total of 12,418,001,077,381,302,684 semigroups of size 10. They only had to find 718,981,858,383,872 by a brute force search, which is 0.006% of the total:I had a much larger "proof", where we didn't bother storing all the details, in which we enumerated 718,981,858,383,872 semigroups, towards counting the semigroups of size 10.
Uncompressed, it would have been about 63,000 terabytes just for the semigroups, and about a thousand times that to store the "proof", which is just the tree of the search.
Of course, it would have compressed extremely well, but also I'm not sure it would have had any value, you could rebuild the search tree much faster than you could read it from a disc, and if anyone re-verified our calculation I would prefer they did it by a slightly different search, which would give us much better guarantees of correctness.
Imagine a business like this: you get highly trained experts to give you their research for free... and then you sell it back to them. Of course these experts need equipment, and they need to earn a living... so you get taxpayers to foot the bill.
And if the taxpayers want to actually read the papers they paid for? Then you charge them a big fee!
It's not surprising that with this business model, big publishers are getting rich while libraries go broke. Reed-Elsevier has a 37% profit margin!
But people are starting to fight back — from governments to energetic students like Alexandra Elbakyan here.
On Friday, the Competitiveness Council — a gathering of European ministers of science, innovation, trade, and industry — said that by 2020, all publicly funded scientific papers published in Europe should be made immediately free for everyone to read.
This will start a big fight, and it may take longer than 2020. But Alexandra Elbakyan isn't waiting around.
In 2011, as a computer science grad student in Kazakhstan, she got sick of paying big fees to read science papers. She set up SciHub, a pirate website that steals papers from the publishers and sets them free.
SciHub now has 51,000,000 papers in its database. In October 2015, Elsevier sued them. In November, their domain name was shut down. But they popped up somewhere else. By February, people were downloading 200,000 papers per day. Even scientists with paid access to the publisher's databases are starting to use SciHub, because it's easier to use.
Clearly piracy is the not the ultimate solution. Elbakyan now lives in an undisclosed location, to avoid being extradited. But she gave the world a much-needed kick in the butt. The old business model of get smart people to work for free and sell the product back to them is on its way out.
For more, read:
The key word here is immediate — right now the US lets the journals sit on publicly funded papers for a year. The Dutch government is really pushing this! Congratulations to them!