
These are photos taken by Hashem Shakeri in Pardis, Iran. These apartment towers were built by the Iranian government when Tehran became overcrowded:
The government responded to the housing shortage by building satellite towns of sterile high-rises on barren land far from the capital. They were supposed to be affordable, ready-made utopias with modern utilities for low-income and middle-class workers who couldn’t afford Tehran. But the early apartments had faulty sewage systems and heating, inadequate access to water, and only intermittent electricity. Many were destroyed in the earthquake of 2017.For more see:Hashem Shakeri first glimpsed some of these ghostly concrete towers on a weekend drive in 2007. He was baffled by the idea that Iranians would be expected to live in the austere structures. "They were like a remote island,” he told me. "When I thought about the people who were supposed to come and live there, I couldn’t even breathe." In 2016, he began to photograph the satellite towns and their residents. He started in Pardis; the name is Persian for "paradise."

The days of the week are named after the classical planets: the 7 things we see going around. It's easier to see if you also know a Romance language like French, or some Norse mythology.
But why are they named in the order that they are? There's an old theory about that.
List the planets by decreasing period. Use each to name one of the \(24 \times 7\) hours of the week. Keep looping around. The first hour of each day gives the name of that day!
Since 24 = 7+7+7+3, we start with Saturday, then go forward 3 steps and get Sunday, and then Monday, and then Tuesday (the day of Mars), and so on.

At least, this is what the Roman historian Dio Cassius (150-235 AD) and the Syrian astrologer Vettius Valens (120-175 AD) claimed.
It's called the theory of planetary hours, and it's in Wikipedia so it must be true!

It's the strongest known acid — so acidic it can't be prepared in bulk. It was one of the first compounds formed in the Universe. It's also the lightest ion made of two different kinds of atoms.
Helium hydride! First created by humans in 1925, it was first seen in outer space in April 2019.
Helium hydride looks like a laugh with a plus sign: HeH+. The cool part, to me, is that extra helium atoms can attach to HeH+ to form larger clusters such as He2H+, He3H+, He4H+, He5H+ and He6H+. Hexahelium hydride is especially stable.
It's a narrow but intriguing speciality: chemistry with just hydrogen and helium! Dihelium hydride can be formed from a dihelium ion and a hydrogen molecule:
People have even studied the ions HeH2++ and HeH2+++. The calculated binding energy of the first is 25.1 kilojoules/mole, while for the second it's only 0.42 kJ/mol. For comparison, that of monatomic hydrogen is 1312 kJ/mol, so these are just barely bound.
For more, see this:
Some recent news: it's a bit harder to destroy HeH+ with electrons than previously thought! So, there must be more in the early Universe. It interacts with the background radiation... so this changes how we interpret cosmological data:

A hydrogen molecule does not look like this! I only just now realized how misleading this picture is. The electron wavefunctions do not form two separate blobs. And of course the 'ball and stick' model is even worse:

In fact a hydrogen molecule is almost round! It looks more like this:

The color and brightness shows how likely you are to find an electron per unit volume. For details on what the colors mean, go here:
Why does this matter?
Here's one reason. When you freeze hydrogen at low pressure it forms a low-density crystal. Since they're almost round and far apart, each molecule can rotate independently!
Since the hydrogen molecules in solid hydrogen are free to rotate, the angular momentum of each one is almost conserved!
Since it's cold, we expect the lowest-energy states to predominate. The two lowest-energy states of a hydrogen molecule are those where the total angular momentum is 0 or 1, depending on whether its proton spins are opposite or aligned. If they are opposite, so the angular momentum is 0, it's called parahydrogen, and this has the lowest energy. If they are aligned, so the total angular momentum is 1, it's called orthohydrogen, and this has the second lowest energy.
So, a crystal of solid hydrogen at low pressures can be made of any sort of mixture of orthohydrogen and parahydrogen! Its properties depend subtly on how much of each. But orthohydrogen has a bit more energy so it slowly turns into the para form.
There are a lot of other weird things about solid hydrogen. It's a 'quantum crystal', meaning the quantum uncertainty in the positions of the nuclei is significant compared to the distance between molecules. It's also extremely compressible.
Only when you compress solid hydrogen a lot — like near the core of
Jupiter — does it become important that the molecules aren't
completely round. Then you get different crystal phases of solid
hydrogen... culminating in a metallic phase that conducts electricity!
October 15, 2019

To get the complex numbers, you take the real numbers and throw in a new number \(i\) that squares to \(-1\). But other alternatives are also interesting! Different choices are connected to geometry in different ways.

The complex numbers, where \(i^2 = -1\), are deeply connected to circles.
The split complex numbers, where \(i^2 = 1\), are connected to hyperbolas.
The dual numbers, where \(i^2 = 0\), are connected to pairs of parallel lines.

You can define exponentials in all three of these number systems. In the complex numbers, they're related to the sine and cosine functions. In the split complex numbers they're related to the hyperbolic sine and cosine functions, \(\sinh x \) and \(\cosh x\). In the dual numbers they reduce to the functions \(1\) and \(x\). These are best linear approximations to the trig functions \( \sin x \) and \(\cos x\), and also the hyperbolic trig functions \( \sinh x \) and \(\cosh x\).
In physics, the complex numbers describe points in 2d space. The split complex numbers describe points in 2d Minkowski spacetime. The dual numbers describe points in 2d Galilean spacetime — the version of spacetime in classical mechanics before special relativity.
In the complex numbers, multiplying by \(e^{ix}\) describes a rotation. In the split complex numbers, it describes a Lorentz transformation in 2d spacetime. In the dual numbers, it describes a Galilean transformation: a transformation to a moving frame of reference in Galilean spacetime.
We can take the real numbers and throw in a number \(i\) that squares to any real number \(q\). By changing \(q\), we can morph the complex numbers to the dual numbers and then split complex numbers. The circle flattens out to an ellipse, then parallel lines, then a hyperbola! In this gif by Tomasz Stachowiak, you can see the ordinary sine and cosine morph to the functions \(x\) and \(1\) and then to the hyperbolic sine and cosine as \(q\) goes from \(-1\) to \(1\):
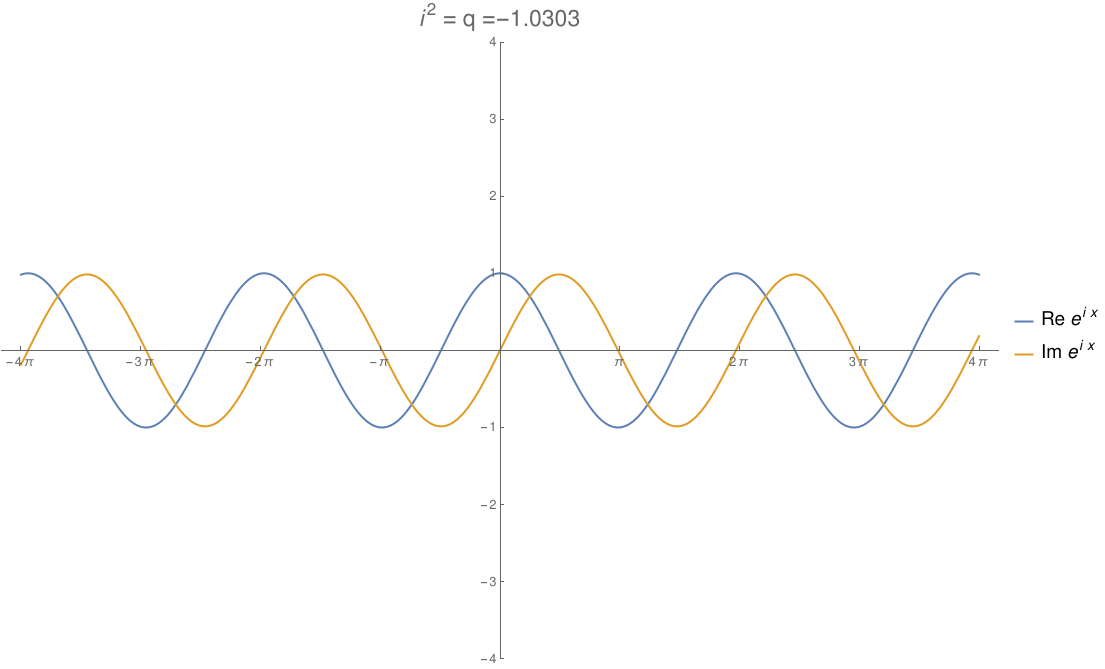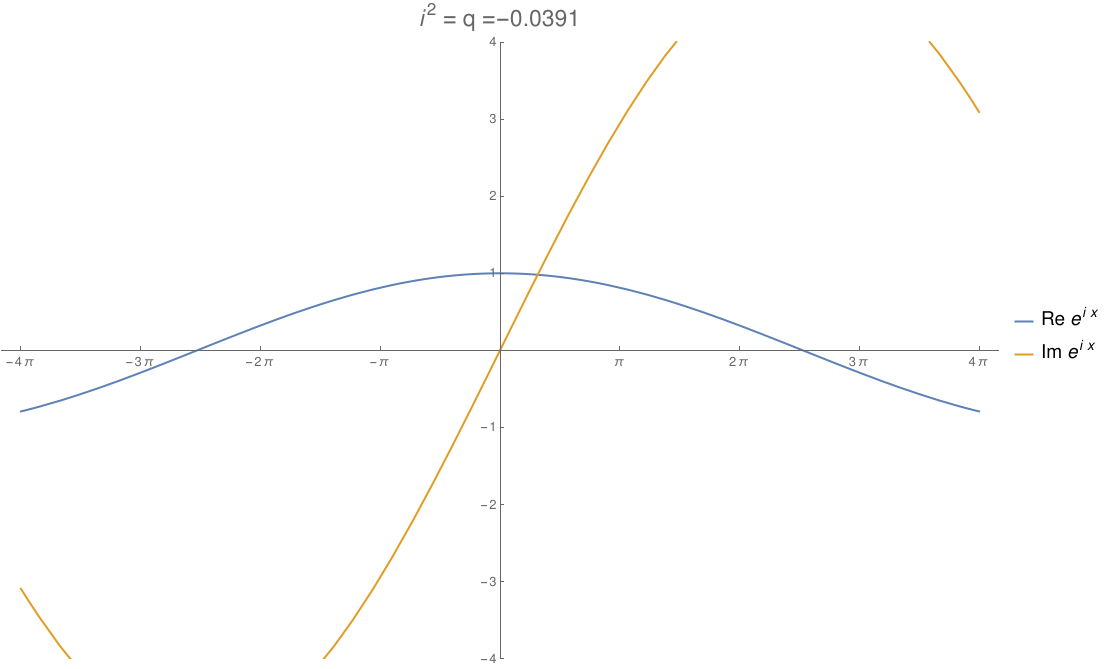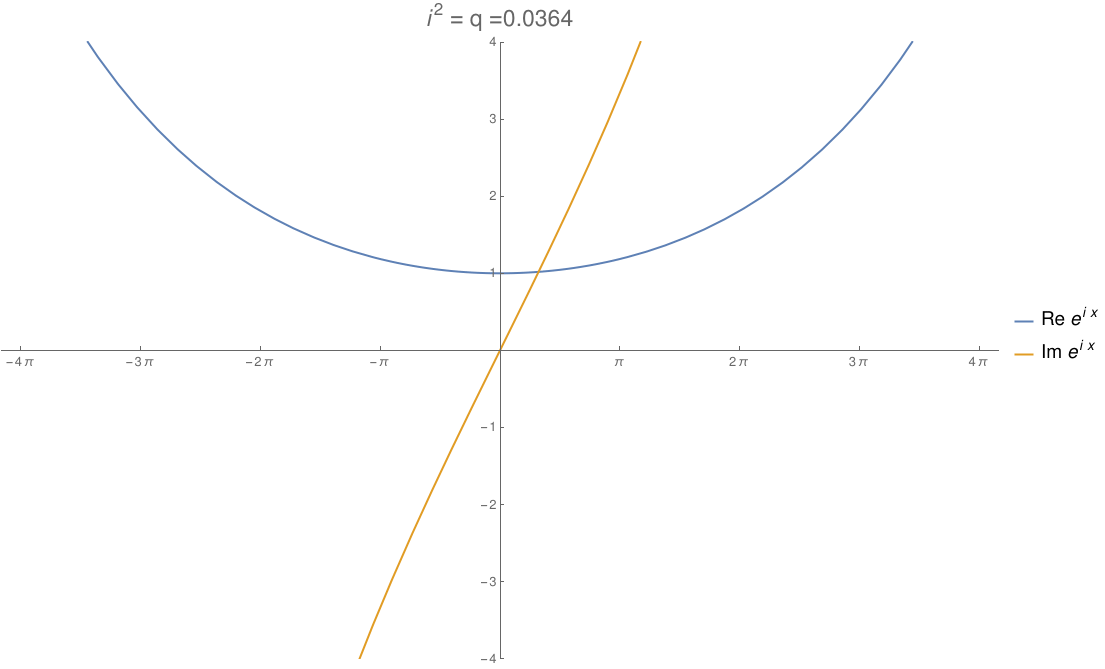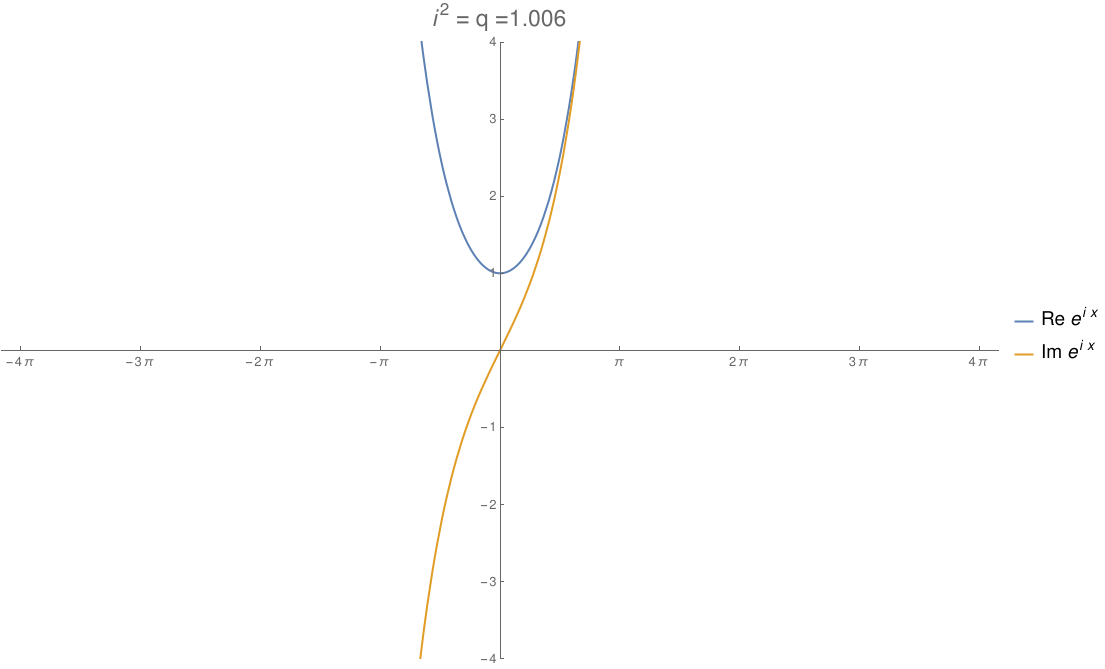
In terms of physics, this number \(q\) is \(1/c^2\), where \(c\) is the speed of light. When \(q\) hits zero, the speed of light becomes infinite and special relativity reduces to the physics of Newton and Galileo. When \(q\) goes negative, time turns into another dimension of space!
The history of these numbers is interesting. In 1848 James Cockle invented 'tessarines' by taking the reals and throwing in two numbers \(i\) and \(j\), where \(i^2 = 1\), \(j^2 = -1\), and \(ij=ji\). His 'real tessarines' \(x + jy\) are the same as split complex numbers.
Later William Kingdon Clifford called split complex numbers 'motors', again seeing them as part of a larger number system, which is now called the split biquaternions.
Clifford introduced the dual numbers in 1873. Later they were studied by Eduard Study, so they're also sometimes called 'Study numbers'.
You can get the dual numbers by taking the real numbers and throwing in a special sort of 'infinitesimal': a number that's not zero, but so small its square is zero. This is the main way we use them now.
They're also an example of a 'Grassmann algebra', also known as an 'exterior algebra'.
I wish more undergrad math courses would spend just a few minutes talking about different number systems — just to let students know we are free to invent and explore.
It's a big world out there! For more, try these:
'Screw theory' was invented by a guy named Ball. There should be a joke in there somewhere. But what is screw theory?
For starters, any rigid motion of 3d Euclidean space has a screw axis: a line mapped to itself. We translate along this axis, and rotate about it.
Screw theory is about the Euclidean group: the group of rigid motion of Euclidean space. A screw is an element of the Lie algebra of this group. It's a 6d vector built from a pair of 3d vectors, an infinitesimal translation and an infinitesimal rotation.
An object moving through space and rotating has a velocity and an angular velocity. These combine to form a screw.
When you push on this object you exert a force and a torque on it. These also combine to form a screw.
Screw theory was developed in the 1800s, and its terminology is cute. The screw combining velocity and angular velocity was called the twist, while the screw combining force and torque was called the wrench.
A lot of good mathematicians worked on screw theory: for example Poinsot, Chasles, Plücker, Klein and Clifford. The fact that every element of the Euclidean group has at least one screw axis is called Chasles' theorem.
These mathematicians defined a dot product and cross product of screws, and did a lot of other things:
The Euclidean group is the semidirect product of the 3d rotation group \(\mathrm{SO}(3)\) and the translation group \(\mathbb{R}^3\). Thus, we can write it as \(\mathrm{SO}(3)\ltimes \mathbb{R}^3\) It's isomorphic to \(\mathrm{SO}(3)\ltimes \mathfrak{so}(3)\), where we use the fact that any Lie group acts on its Lie algebra — which we can treat as a vector space, and thus an abelian Lie group. In fact any Lie group \(G\) acts on its Lie algebra \(\mathfrak{g}\) and gives a Lie group \(G\ltimes \mathfrak{g}\). This is isomorphic to the tangent bundle \(\mathrm{T}G\). So the tangent bundle of a Lie group is again a Lie group!
Putting all this together, the Euclidean group is isomorphic to the tangent bundle \(\mathrm{TSO}(3)\). A screw is an element of the Lie algebra of this! A less fancy way to say it: screws live in \(\mathfrak{so}(3)\ltimes \mathbb{R}^3\).
The cross product of screws is the Lie bracket in \(\mathfrak{so}(3)\ltimes \mathbb{R}^3\). The dot product is the obvious invariant inner product on this Lie algebra.
But in the 1800s, people preferred quaternions! So they had a different story.
We can think of \(\mathfrak{so}(3)\) as the imaginary quaternions \(\{ai+bj+ck\}\). Thus, we can think of \(\mathfrak{so}(3)\ltimes \mathbb{R}^3\) as the imaginary quaternions tensored with the dual numbers \(\mathbb{R}[\epsilon]/\langle \epsilon^2\rangle\).
Using these ideas, Clifford thought of screws as sitting inside the algebra of quaternions tensored with the algebra of dual numbers. He called this 8-dimensional algebra the dual quaternions:
In the dual quaternions, the infinitesimal rotations are guys like \(ai+bj+ck\), while the infinitesimal translations are guys like \(\epsilon(ai+bj+ck)\). Together these form the 'screws'.
The screws are closed under commutators! They form the Lie algebra of the Euclidean group.
The dual quaternions can also be seen as the Clifford algebra of a real vector space with a quadratic form of signature \(+\!+0\), using the conventions of my last diary entry. The three generators are \(i, j\) and \(\epsilon k\). But this is annoying asymmetrical! A better description is that the dual quaternions are the even part of the Clifford algebra of a vector space with form of signature \(+\!+\!+ 0\):
Nowadays screw theory is used in robotics — usually without all this fancy algebra. Here's a typical intro:
But there will be even be a workshop about applications of dual quaternions to robotics at ICAR 2019, the International Conference on Advanced Robotics. And Dan Piponi writes:
They're also used in movie visual effects to simulate rigid-body dynamics. E.g. if you want to simulate a body thrown off a building without putting a stuntperson at risk.I like the idea of the dual quaternions as an 'infinitesimal thickening' of the quaternions, and the Euclidean group \(\mathrm{TSO}(3)\) as an 'infinitesimal thickening' of the rotation group. Rogier Brussee writes:
In algebraic geometry what you would do is consider the affine algebraic group \(SO(V,g)\ltimes V\) which is defined by polynomial equations inside \(\mathrm{End}(V)\times V\) i.e. by an algebra \(H = k[X_{ij}, T_i]/I\). The group structure is equivalent to a commutative but not cocommutative Hopf algebra structure \(\Delta \colon A \to A\otimes A\) and \(S\colon A \to A\).Let \(\mathfrak{m}\) be the maximal ideal of the identity. Then we can consider the Hopf algebra \(A/\mathfrak{m}^2\).
This construction works for all algebraic groups, and gives an algebraic group \(\mathrm{Spec}(A/\mathfrak{m}^2)\) with only one point and a non reduced structure (i.e. one that has nilpotent 'functions'). Apparently if \(V\) is 3-dimensional and we take the algebraic group \(\mathrm{SO}(V,g)\ltimes V \) the algebra of 'functions' splits over \(k[\epsilon]/\langle\epsilon^2\rangle\)!
Carbon has many forms, but this one was purely theoretical until recently. Now scientists have made a cyclocarbon!
The strain on the triple bonds is very high when you bend them. So you need at least 18 atoms to make a ring like this, and that's what they did.
Scientists at IBM and Oxford took the molecule at left, lying on a salt crystal, and used a very sharp needle to push out the 3 parts containing oxygen. It's called atomic force microscopy and yes, it lets you manipulate individual molecules!

"Dodecahedrane" is a molecule with 20 carbons and 20 hydrogens, shaped like a dodecahedron. It took chemists over 30 years to make this once they got the idea of trying.
What's cooler than making dodecahedrane?
It's making dodecahedrane and then shooting helium ions at it to create the world's smallest helium balloons!
The result, called He@C20H20, consists of a dodecahedrane molecule with helium atom trapped inside. It was first made in 1999:
I'm getting bored sitting here. Let's start using some of these newer tilings!
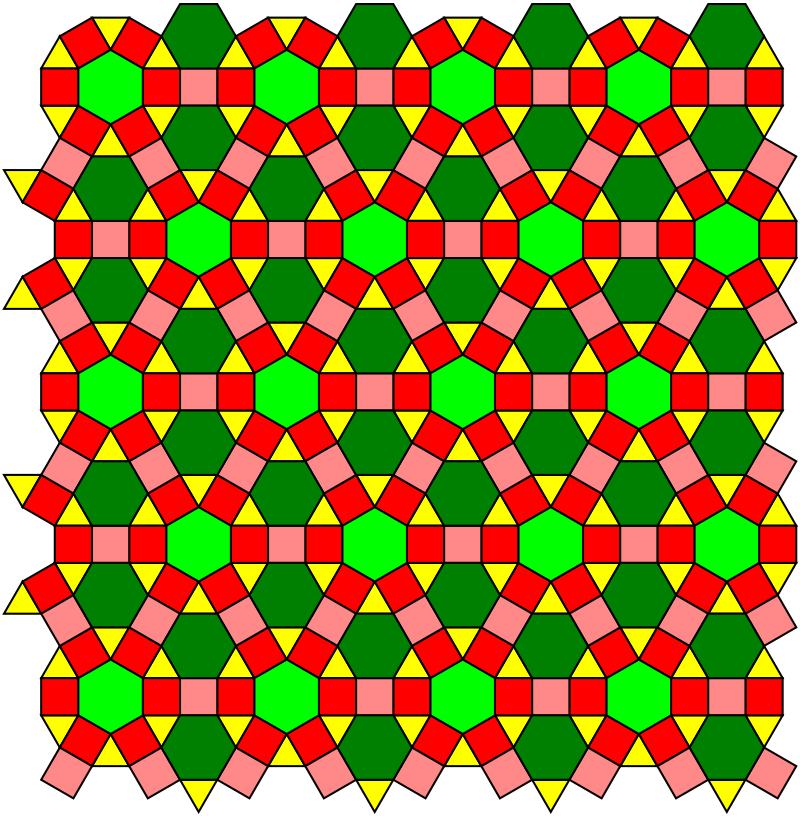
A '\(k\)-uniform tiling' is one made from regular polygons where there are \(k\) different kinds of vertices. When \(k = 1\) they're called 'uniform' tilings, and there are 11 kinds. This is probably my favorite — it's called the '4.6.12 tiling':
It's beautiful. But come on, folks, let's start using \(k > 1\) in public restrooms!
There are twenty 2-uniform tilings. This one is a spiced-up version of the 4.6.12 tiling:
Again it has vertices where a square, a hexagon and a dodecagon meet... but now also vertices where a triangle, 2 squares and a hexagon meet. Nice!
Next, another variation on the same theme. This is one of the 61 different 3-uniform tilings:
And here's one of the 151 different 4-uniform tilings:
Here's another 4-uniform tiling — this one has some nice 'hexagons with rounded corners' built in:
There are 332 5-uniform tilings, and 673 6-uniform ones. At that point people gave up counting. There's no reason we need to be bored in bathroom stalls.
All these tilings were drawn by Tom Ruen and placed on Wikicommons:
All the vertices are of type 4.6.12 or 3.4.6.4. But if you examine
sufficiently large neighborhoods of these vertices you'll see they
come in four kinds! In other words, the symmetry group of this tiling
does not act transitively on the set of vertices: there are four orbits.
October 29, 2019
CH2N2. Bad stuff.
Well, actually are other chemicals with formula CH2N2.
Two of them are called 'cyanamide'. Because they easily turn into each other, they are called 'tautomers'. Above is the more stable form, the 'nitrile' form.
Below is the less stable form of cyanamide, the 'carbodiimide' form. Here the hydrogens are at opposite ends of the molecule, not the same end.
There are also other molecules made of two carbons, two hydrogens and a nitrogen!
Here are some scary tales of working with diazomethane:
Lowe begins as follows:
That diazo group is looking for an excuse to revert back to nitrogen gas, which process comes with an inevitable no-substitutions side order of kaboom. The chemist’s job is to not give it that excuse. That means that you can’t heat the stuff up, you don’t make it very concentrated, and you don’t even expose it to sharp or rough surfaces, because that can be enough right there. They sell distillation glassware specifically for diazomethane preps, with weirdly glossy ground-glass joints.
Then come the horror stories. On Twitter someone had an even more horrific story:
When I was an undergraduate,one of the pre-meds lost an eye working with diazo, as we called it back then.She was screaming, "Why do I have to understand this crap to become a doctor?!? All I have to do is know enough to con people into making me rich!"

Take the real numbers. Throw in some square roots of +1 and some square roots of -1, all anticommuting. You get a Clifford algebra.
Clifford algebras are important in geometry and physics — we need them to understand spin! They also display some amazing patterns.
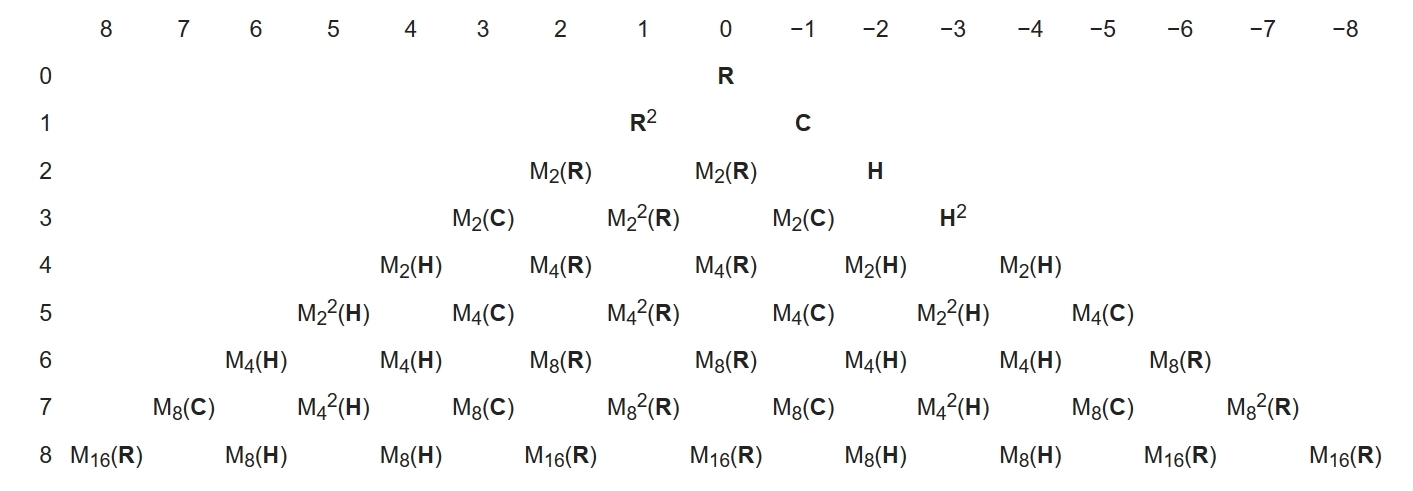
Here's a table of the Clifford algebras for \(\mathrm{C}\ell_{p,q}\) for \(p + q \le 8\). \(p+q\) runs vertically and \(p-q\) runs horizontally: for example \(\mathrm{C}\ell_{1,3} = \mathrm{M}_2(\mathbf{H})\) is in row \(4\), column \(-2\).
Puzzle. How many patterns can you see in this table?
The table stops here because if you throw 8 more anticommuting square roots of \(+1\) into a Clifford algebra, you get \(16\times 16\) matrices with entries in that Clifford algebra. This is also true if throw in 8 more anticommuting square roots of \(-1\), or 4 more anticommuting square roots of \(+1\) and 4 more anticommuting square roots of \(-1\). In other words: $$ \mathrm{C}\ell_{p+8,q} \cong M_{16}(\mathrm{C}\ell_{p,q}) $$ $$ \mathrm{C}\ell_{p,q+8} \cong M_{16}(\mathrm{C}\ell_{p,q}) $$ $$ \mathrm{C}\ell_{p+4,q+4} \cong M_{16}(\mathrm{C}\ell_{p,q}) $$
Here's one pattern: directly below any Clifford algebra is the algebra of \(2 \times 2\) matrices with entries in that Clifford algebra! For example directly below \(\mathbf{C}\) is \(\mathrm{M}_2(\mathbf{C})\), and directly below that is \(\mathrm{M}_4(\mathbf{C})\), which is \(\mathrm{M}_2(\mathrm{M}_2(\mathbf{C}))\), since \(2\times 2\) matrices of \(2 \times 2\) matrices are \(4 \times 4\) matrices!
What other patterns can you see?
On Twitter Ron Jones asked:
Why isn't \(\mathbf{H} \cong \mathrm{C}\ell_{0,3}\)?The reason is that \(\mathbf{H}\) is generated by two square roots of -1, for example \(i\) and \(j\). This gives $$ 1, i, j, ij $$ and everything else can be simplified using \(i^2 = j^2 = -1\) and \(ij = -ji\). In particular if we let \(k = ij\), we can show \(k^2 = -1\), \(ik = -ki\) and \(jk = -kj\). So \(\mathbf{H} \cong \mathrm{C}\ell_{0,2}\).
If you start with three anticommuting square roots of -1, they generate an 8-dimensional algebra... and you can see from the table that this consists of pairs of quaternions! It's fun to check this.
Also on Twitter, William Ricker was curious about why \(M_2(\mathbf{R})\) is both \(\mathrm{C}\ell_{2,0}\) and \(\mathrm{C}\ell_{1,1}\).
Here's why the algebra of \(2\times 2\) real matrices is isomorphic to \(\mathrm{C}\ell_{2,0}\). Here are two anticommuting square roots of \(1\) that generate all the \(2\times 2\) real matrices: $$ \left( \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array}\right) $$ and $$ \left( \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array}\right) $$ That is, if we call the first matrix \(i\) and the second one \(j\), we have $$ i^2 = j^2 = 1 $$ $$ ij = -ji $$ and every \(2 \times 2\) real matrix can be written as $$ a1 + bi + cj + dij $$ for unique real numbers \(a,b,c,d\). It's fun to check this! This is how you get started on Clifford algebras.
But you can find two other \(2 \times 2\) real matrices \(e\) and \(f\) such that $$ e^2 = 1, \, f^2 = -1 $$ $$ ef = -fe $$ and every \(2 \times 2\) real matrix can be written as $$ a1 + be + cf + def $$ for unique real numbers \(a,b,c,d\). So the algebra of \(2 \times 2\) real matrices is also isomorphic to \(\mathrm{C}\ell_{1,1}\).