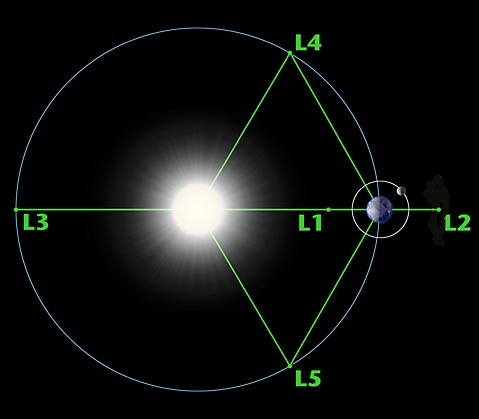
These are all jargon for places where a light third body can sit "motionless" relative to two heavier bodies that are orbiting each other thanks to the force of gravity.
For example: imagine the Earth going around the Sun in a circular orbit. Then there are five Lagrange points where we can put a satellite. Three of them lie on a line through the Sun and the Earth. L1 is between the Sun and Earth, L2 is in the same direction as the Earth but a bit further out, and L3 is opposite the Earth, very slightly further out:
By the way, both pictures on this website were created by Neil Cornish and other scientists who are studying the microwave background radiation with the help of a satellite called WMAP, located at the Lagrange point L2. You can click on these pictures to see more about this.
The Earth, Sun and Lagrange point L4 (or L5) form the vertices of an equilateral triangle.
The really interesting thing is that the Lagrange points L4 and L5 are stable equilibria as long as the heavy body — the Sun in our example — is more than 24.96 times as massive as the intermediate-sized one. In other words, a small body put in orbit at the right speed at either of these points will tend to stay there! If you nudge it a little, it will drift back.
On the other hand, L1, L2, and L3 are unstable equilibria: the slightest nudge will make satellite at one of these points drift away. To keep it there, you'll need to equip it with thrusters that keep correcting its orbit now and then.
The stable Lagrange points are the most interesting for astronomy, because stuff tends to accumulate there. For example...
The asteroid belt is the green stuff — ignore that. Look for Jupiter moving along the outermost circle, and see how the blue dots are clustered 60 degrees ahead and behind Jupiter. These are the Trojan asteroids!
The first of these was discovered by the German astronomer named Max Wolf in 1906, using a technique he pioneered: comparing two photographs taken on different night and seeing if any of the "stars" had moved. He discovered lots of asteroids this way! The first Trojan he discovered is called 588 Achilles, since it was the 588th asteroid to be discovered. It's 116 kilometers in diameter.
In general, the Trojan asteroids at L4 are named after Greek soldiers in the Trojan war, like Achilles, Nestor, Agamemnon and Odysseus. Those at L5 are named after guys on the Trojan side, like Patroclus, Priamus, and Paris.
I must thank Eric Vosselmans for informing me of the only two exceptions: Hektor, the Trojan prince who somehow wound up at L4, and Patroclus, the Greek companion of Achilles who accidentally strayed over to L5. But basically it's Greeks at L4, Trojans at L5:
For some mysterious reason there are more big asteroids at L4 than L5. Maybe this is why the Greeks won the war! But seriously: why are there more asteroids at L4? One of my correspondents has suggested a simple explanation: as Jupiter runs into asteroids, they tend to get stuck at L4 because it's in front of Jupiter. Could that be all there is to it? Maybe this could make a nice Ph.D. thesis in astrophysics.
The asteroid 5261 Eureka is a "Mars Trojan", occupying the L5 point of Mars' orbit around the sun. It was discovered by David Levy in 1990. It's reddish in hue and it's deep within the stable Lagrangian zone of Mars, which suggests that it's been in this orbit for most of the history of the Solar system.
Some other Mars Trojans have been discovered since — at least four at L5 and one at L4. Hmm, this time there are more at L5! The plot thickens.
When I last checked, there were no known Saturn Trojans, but seven "Neptune Trojans", with unglamorous names 2001 QR322 and 2004 UP10. Asteroids in the outer solar system are called "Centaurs", but not too many are known. As of 2005, only about forty Centaurs are known that enter the region between Saturn and Uranus.
Why so few? Well, most of these have been discovered since 2000, so we may just be starting to find them. But, researchers at the University of California at Los Angeles and elsewhere have done some computer simulations to study this question. They found that niches for stable orbits are rare in the outer solar system. Amusingly, they named the hypothetical Saturn Trojans "Bruins". Why? Because that's what UCLA's football team is called — and they wanted to get back at astronomers at the University of Southern California, whose football team is called the Trojans!
Unfortunately, the Trojans are way ahead of the Bruins.
Are there any "Earth Trojans" — asteroids at the Lagrange points of the Earth's orbit around the Sun?
Yes! But only two have been found so far, both at Earth's L4 point: 2010 TK7, which is 300 meters across, and 2020 XL5, which is about 1200 meters across. As their names indicate, they were found in 2010 and 2020:
Why so few Earth Trojans, and discovered so recently? One reason is that the L4 and L5 points are just 60° from the Sun, so we mainly see the shadowed side of any asteroid there. To see them at night they must be at least 30° away from the vertical, so we must look through quite a bit of atmosphere. The closer to vertical they become, the brighter the sky becomes. To add to the difficulty, there is zodiacal light to contend with, caused by interplanetary dust in the plane of the Earth's orbit. The problems were discussed here in 1999:
Current telescopes and detectors should easily be able to detect ETAs [Earth Trojan Asteroids], their proximity to both Earth and the Sun making them relatively bright. However, searches for such objects are not without their difficulties. The nearness of these bodies to Earth means that any Trojan group would cover a large projected area on the sky; we will see [...] that such a cloud may extend over hundreds of square degrees with only a very broad central peak. As well, the necessary proximity of these asteroids to the triangular Lagrange points requires observations to be made in the morning and evening, and hence subject to higher airmasses and the increased sky brightness of twilight. Observational searches for ETAs thus present interesting challenges.
Our planet also has some other amazing companions that aren't Trojans. The best known is the asteroid 3753 Cruithne. Cruithne is not at a Lagrange point. Instead, it moves in a very complicated spiralling horseshoe-shaped orbit relative to the Earth! For a beautiful discussion of this by the discoverers of this phenomenon, complete with animated movies, see:
An even more complicated companion asteroid of the Earth is called 2002 AA29. It oscillates between being a quasi-satellite of the Earth and having a horseshoe orbit!
What about the Lagrange points of the Moon's orbit around the Earth? Is anything lurking there? If the Earth had any smaller moons besides the one we all know, this is where they'd probably be!
In fact, people have been looking a long time for extra moons orbiting the Earth. Some people even claimed to find them! The history is pretty interesting. It began when Frederic Petit claimed three observers had seen a small second moon... but it picked up steam when Jules Verne read about this and put it in his novel From the Earth to the Moon:
""Is that possible?", exclaimed Michel Ardan, "the earth has two moons?"This got amateur German astronomers searching for a little moon they called "Kleinchen"... and in 1898, one Dr. Georg Waltemath claimed to have found a whole system of small moons! In 1918, an astrologer even added an extra moon to his horoscopes: the dark moon "Lilith". For more of this amusing history, you've gotta read this:"Yes, my friend, it has two moons, although it is usually believed to have only one. But this second moon is so small and its velocity is so great that the inhabitants of Earth cannot see it. It was by noticing disturbances that a French astronomer, Monsieur Petit, could determine the existence of this second moon and calculated its orbit. According to him a complete revolution around the Earth takes three hours and twenty minutes.... "
However, the most recent and scientific search for objects at the Earth-Moon Lagrange points seems to be this:
Believe it or not, Freitas claims to have found an alien spacecraft at L4!
Just kidding... this isn't one of those crackpot websites you've probably seen. Actually, his search proved that no solid object the size of Skylab or larger is parked at L4 or L5.
But that doesn't mean these places are completely boring. In fact, there are dust clouds at L4 and L5. They're about four times as big as the Moon. They're very wispy and insubstantial, but they've been photographed a couple of times. In 1990 the Polish astronomer Winiarski found that they are a few degrees in apparent diameter, that they drift up to ten degrees away from the Lagrange points, and that they're somewhat redder than the usual "zodiacal light" — the light reflecting off dust in the solar system.
In 1974, a physics professor at Princeton wrote a paper that advocated putting space colonies at one of the Earth's Lagrange points, namely L5:
The idea caught on and an organization formed to advocate doing this: the L5 Society! They merged with the National Space Society in 1987, but you can still read their old newsletters:
But so far, it seems there's just dust at the Earth-Moon Lagrange points. So, what about the Lagrange points of moons of other planets?
Well, Saturn has an icy moon called Dione, 560 kilometers in diameter — and 60 degrees ahead of Dione, right at the Lagrange point L4, there is a tiny moon called Helene! Here's a picture of Helene:
There's also a tiny moon called Polydeuces trailing behind Dione at the L5 point: Even better, Saturn has another moon called Tethys, quite similar to Dione, 530 kilometers in diameter, which has two Lagrange moons. There's a little one called Telesto at the L4 point, 60 degrees ahead of Tethys, and another little one called Calypso, 60 degrees behind Tethys!
Does anyone know other natural occupants of Lagrange points? You'd think that some of the big moons of Jupiter would have some of their own Trojans. Jupiter has plenty of moons: Metis, Adrastea, Amalthea and Thebe, Io, Europa, Ganymede, Callisto, Leda, Himalia, Lysithea, Elara, Ananke, Carme, Pasiphae and Sinope, and eleven more discovered in 2000 and named in 2004. But I don't know any of these that are sitting at Lagrange points!
This leaves artificial satellites of the man-made sort.
Despite the desires of the L5 society, I don't know of man-made satellites at the Lagrange points of the Earth-Moon system. However, people are already putting artificial satellites at the Lagrange points of the Earth's orbit around the Sun! L1 is home of SOHO, the Solar and Heliospheric Observatory. This allows SOHO a nice clear view of the Sun. In April 2001, NASA put a satellite called WMAP into the Lagrange point L2. WMAP stands for Wilkinson Microwave Anisotropy Probe: it measured bumps in the cosmic microwave background and discovered amazing things about the amount of dark matter and dark energy in the universe.
Amusingly, a blob of dust trailing the Earth showed up nicely in measurements of the cosmic infrared background radiation by a precessor of WMAP, the famous satellite COBE:
This blob has a radius of about a tenth that of the earth's orbit. So far, attempts to find similar dust clouds at the Lagrange points of Mars and Jupiter have failed:
Perhaps the asteroids there screw things up?
In fact, they've already used the IPS for a number of space missions, including the Genesis mission - the one that collected samples of solar wind, then came back to Earth... and then crashed into the desert in Utah at 320 kilometers per hour because of a faulty switch.
I hadn't heard about the interplanetary superhighway until Nathan Urban explained it to me. Here's what he said:
I've just recently been reading about the "Interplanetary Superhighway" (IPS). Have you heard of it? If not: It turns out that the L1 and L2 points act as "gateways" for very low-energy transfer orbits — better than Hohmann transfers. The IPS works by transferring between unstable and stable manifolds winding off and on unstable orbits like at L1 and L2.Nathan also sent me a lot of cool links to more information on the interplanetary superhighway. You can find these at the end of this page.The recent Genesis probe, the one that crashed, used such an orbit. It went out to the Earth-Sun L1 point, made 5 orbits on some crazy Lissajous curve to collect the solar wind, then returned back to Earth, passing by the L2 point to delay reentry until daylight in Utah for the planned helicopter capture — all without deterministic trajectory changes! They did have to use engines to correct the orbit, since they didn't get it exactly right and there were other requirements of the spacecraft, but in principle you could come up with a wacky orbit like this that would have completed the entire Genesis mission and returned the probe to Utah without any course corrections past the initial boost.
In fact, you can design an orbit that goes around the Sun some number of times, the Earth-Sun L1 point some number of times, the Earth some number of times, the L2 point some number of times, and the region outside the Earth's orbit some number of times — for any list of numbers you want!
Before being fully understood as such, the IPS was first used in the ISEE3 mission in 1978. Later in 1991, it was used to rescue a Japanese satellite called Hiten stranded in the wrong orbit without enough fuel to reach the proper orbit by traditional means like Hohmann transferring.
As you mention on your page, it's now popular to put satellites (like Genesis, SOHO, WMAP) etc. in "halo orbits" at Sun-Earth Lagrange points. Well, it turns out that using an IPS trajectory, you can go from the Earth-Moon L1 point to the Sun-Earth L1 point or back with a course correction of only 50 meters/second!! This has led to a proposal for a "Lunar L1 Gateway", a manned space station at the lunar L1 point that can be used to service missions at the solar L1 point — just bring them back to the gateway station for servicing, and send them back to their halo orbits afterwards, with almost no fuel.
They've also used the IPS to design a Jovian "Petit Grand Tour" mission to visit four of the Jovian moons on a screwy trajectory that has it oribiting each moon a certain number of times and going on to the next, using little or no fuel.
It has been shown that Comet Shoemaker-Levy 9, the one that crashed into Jupiter, was following one of these chaotic IPS orbits through a Lagrange point. Apparently there is some evidence that the dinosaur-killer asteroid followed one to Earth.
I found the IPS to be an interesting application of chaos theory... you heard a lot about it in the '80s and early '90s, it was very faddish, then you didn't hear much about it anymore... this is one application not just for pure science (e.g., stability of the solar system), but applied science (transportation within the solar system).
Finally, before I quit, I want to say a bit about the fascinating mathematics of Lagrange points.
In 1772, Joseph-Louis Lagrange shared a prize with Euler for work on the orbit of the Moon. Euler had discovered L1, L2, and L3, but Lagrange did a more complete analysis of the problem including L4 and L5 in his Essai sur le problème des trois corps. You can read this paper if you go here, choose "Lagrange" as the author, select the 6th volume of "Oeuvres / Joseph Louis de Lagrange. 6 / publ. par les soins de J.-A. Serret" and go to page 229.
For a modern proof that there are exactly five Lagrange points, formulas for where they are located, and a proof that L4 and L5 are stable while the other three are not, try this:
I can sketch the argument here, but it gets pretty tricky when it comes to the stability of L4 and L5.
Let's use the Sun-Earth system as an example. If we work in a coordinate system that rotates around the Sun along with the Earth, we see that a light third body would be affected by four forces:
Thus, to find the Lagrange points we need to see where the gravitational force and centrifugal force cancel out. One can work out where this happens:
In some cases this is actually easy to see without any calculations. For example, suppose we have a body perched at L1, between the Sun and the Earth. If it moves any closer to the Earth it will be more attracted to the Earth, because the Earth's pull will be stronger and the Sun's weaker. Similarly, if it moves any closer to the Sun it'll be more attracted to the Sun. So, it's like a ball sitting on a hilltop: the slightest nudge in either direction and it will roll off! That's why see blue arrows pointing to left and right at L1.
Similarly, suppose we have a body at L2. If it moves closer to the Earth it will be more attracted to the Earth, because both the Earth's and Sun's pull will be stronger — this time they're pulling in the same direction. Conversely, if it moves away from the Earth it will be less attracted to the Earth. So again, we see blue arrows pointing to the left and right at L2. L3 is similar.
It's a little harder to intuitively explain the red arrows at L1, L2 and L3, but it's not all that hard for L1 and L2. Think about it.
The really tricky cases are L4 and L5. It's hard to see why these are places where the gravitational force plus centrifugal force add to zero. And it's even harder to see why these are more stable locations than L1, L2, or L3.
In fact, these Lagrange points look even worse than L1, L2 or L3, since they have no red arrows: no directions you can nudge an object where it will tend to move directly back.
But in these cases, the Coriolis force also plays a crucial role! If the object at L4 or L5 starts moving either towards or away from the Sun, the Coriolis force will push it to one side, sending it into orbit around the Lagrange point! And it turns out this effect manages to stabilize the equilibria at L4 and L5.
This argument should not be enough to convince you - and indeed, I don't see an easy way to explain this stuff to a skeptic using nothing but plain English. Cornish's mathematical proof uses calculus and matrices! It's not that complicated... but it's a great example of how gravity has tricks up its sleeves that can only be revealed using math.
Near-Earth asteroids (or NEAs) are our closest neighbours in the Solar System — some of these objects have been known to pass closer to the Earth than the Moon. These objects, which range in size from 40 km to a few metres, are important to our understanding of past and present Earth impact rates, and are likely to prove useful as bases and/or mineral sources as humans move into near-Earth space. Here we report that the near-Earth asteroid 3753 (1986 TO) is in an unusual horseshoe-type orbit about that of the Earth. Horseshoe orbits, so named because of their shape in a reference frame which corotates with their accompanying planet, are a well-known feature of the three-body problem. However, only one instance of this type of interaction has been observed in nature, involving the Saturnian satellites Janus and Epimetheus, and this system's behaviour is much less intricate than that of 3753. This asteroid is unique: it is an example of a rare type of dynamical relationship, and although it is not a satellite of our planet per se, it is, apart from the Moon, the only known natural companion of the Earth.
Observational searches for asteroids orbiting near Earth's triangular Lagrange points face unique obstacles. A population of such asteroids would occupy a large projected area on the sky (possibly hundreds of square degrees) and is not favorably placed with respect to the Sun. Here we examine the properties of synthetic populations of Earth "Trojans" in order to aid in the optimization of observational searches for them. We find that the highest on-sky projected number densities are not located at the positions of the L4 and L5 points themselves, but rather a few degrees closer to the Sun. Also, asteroids on orbits about the L4 and L5 points typically brighten as the difference between their ecliptic longitude and that of the Sun increases owing to phase effects, but their number density on the sky concurrently falls rapidly.
The last few months have seen the discovery of a second Martian Trojan (1998 VF31), as well as two further possible candidates (1998 QH56 and 1998 SD4). Together with the previously discovered Martian satellite 5261 Eureka, these are the only known possible solar system Trojan asteroids not associated with Jupiter. Here, maps of the locations of the stable Trojan trajectories of Mars are presented. These are constructed by integrating an ensemble of in-plane and inclined orbits in the vicinity of the Martian Lagrange points for between 25 million and 60 million years. The survivors occupy a band of inclinations between 15 degrees and 40 degrees and longitudes between 240 degrees and 330 degrees at the L5 Lagrange point. Around the L4 point, stable Trojans inhabit two bands of inclinations (15° < i < 30° and 32° < i < 40°) with longitudes restricted between 25 degrees and 120 degrees. Both 5261 Eureka and 1998 VF31 lie deep within one of the stable zones, which suggests they may be of primordial origin. Around Mars, the number of such undiscovered primordial objects with sizes greater than 1 km may be as high as 50. The two candidates 1998 QH56 and 1998 SD4 are not presently on Trojan orbits and will enter the sphere of influence of Mars within half a million years.
We investigate the stability regions of hypothetical terrestrial planets around the Lagrangian equilibrium points L4 and L5 in some specific extrasolar planetary systems. The problem of their stability can be treated in the framework of the restricted three body problem where the host star and a massive Jupiter-like planet are the primary bodies and the terrestrial planet is regarded as being massless. From these theoretical investigations one cannot determine the extension of the stable zones around the equilibrium points. Using numerical experiments we determined their largeness for three test systems chosen from the table of the know extrasolar planets, where a giant planet is moving close to the so-called habitable zone around the host star in low eccentric orbits. The results show the dependence of the size and structure of this region, which shrinks significantly with the eccentricity of the known gas giant.
We simulated more than a hundred possible orbits of the Neptune Trojan 2001 QR322 for the age of the Solar system. The orbits were generated randomly according to the probability density derived from the covariance matrix of the orbital elements. The test trajectories librate around Neptune's L4 point, with amplitudes varying from 40° to 75° and libration periods varying from 8900 to 9300 years. The ν18 secular resonance plays an important role. There is a separatrix of the resonance so that the resonant angle switches irregularly between libration and circulation. The orbits are chaotic, with observed Lyapunov times from 1.7 to 20 Myr, approximately. The probability of escape to a non-Trojan orbit in our simulations was low, and only occurred for orbits starting near the low-probability edge of the orbital element distribution (largest values of initial semimajor axis and small eccentricity). This suggests that the Trojan may well be a primordial object.
Using the Canada-France-Hawaii 3.6 m telescope and the new CFH12k wide-field CCD imager, a survey of the region near Earth's L4 (morning) Lagrange Point was conducted in May and July/August 2000, in hopes of finding asteroids at or near this point. This survey was motivated by the dynamical interest of a possible Earth Trojan asteroid (ETA) population and by the fact that they would be the easiest asteroids to access from Earth. Recent calculations (Wiegert, Innanen and Mikkola, 2000, Icarus 145, 33-43) indicate stability of objects in ETA orbits over a million year timescale and that their on-sky density would be greatest roughly five degrees sunward of the L4 position. An optimized search technique was used, with tracking at the anticipated rate of the target bodies, near real-time scanning of images, and duplication of fields to aid in detection and permit followup. Limited time is available on any given night to search near the Lagrange points, and operations must be conducted at large air mass. Approximately 9 square degrees were efficiently searched and two interesting asteroids were found, NEA 2000 PM8 and our provisionally named CFZ001. CFZ001 cannot be excluded from being an Earth Trojan although that is not the optimal solution for the short arc we observed. This object, of R magnitude 22, was easily detected, suggesting that our search technique worked well. This survey supports the earlier conclusion of Whitely and Tholen (1998, Icarus 136, 154-167) that a large population of several hundred meter diameter ETAs does not exist. However, our effective search technique and the discovery of two interesting asteroids suggest the value of completing the survey with approximately 10 more square degrees to be searched near L4 and a comparable search to be done at L5. Funding from Canada's NSERC and HIA and the Academic Research Fund of Athabasca University is gratefully acknowledged.
Numerical simulations of the orbital evolution of asteroidal dust particles show that the Earth is embedded in a circumsolar ring of asteroidal dust, and has a cloud of dust permanently in its wake. This could account for the asymmetry of the zodiacal cloud observed by the Infrared Astronomical Satellite (IRAS). The resonant trapping and subsequent release of dust particles by the ring may provide a mechanism by which carbonaceous material is transported from the asteroid belt to the Earth.
We investigate the possibility that fractions of the primordial populations at the triangular Lagrangian points of Saturn, Uranus, and Neptune have survived to the present and form (as yet unobserved) clusters of bodies coorbiting with these planets. Such leftovers would be analogs of the numerous objects (Trojans) leading and trailing the revolutions of Jupiter around the Sun. We focus on the dynamical stability of such populations over the age of the Solar System, assuming the current configuration of planets, and also discuss effects of the early radial migration of the outer planets. Our results suggest that, while Saturn's and Uranus' primordial Trojan populations should have been depleted by a factor of 100, Neptune may retain 50% of its original population of Trojans. A population of neptunian Trojans comparable to, or even larger than, Jupiter's Trojan population cannot be ruled out by existing observations. We compute the present-day sky densities of the hypothetical Trojans of the outer planets which can be used to guide observational surveys. Finally, we propose that the long-term instabilities that cause some jovian Trojans to escape the region of the Lagrange points at the present are due to three-body resonances.
The regions around the L4 and L5 Lagrangian points of Jupiter are populated by two large swarms of asteroids called the Trojans. They may be as numerous as the main-belt asteroids and their dynamics is peculiar, involving a 1:1 resonance with Jupiter. Their origin probably dates back to the formation of Jupiter: the Trojan precursors were planetesimals orbiting close to the growing planet. Different mechanisms, including the mass growth of Jupiter, collisional diffusion, and gas drag friction, contributed to the capture of planetesimals in stable Trojan orbits before the final dispersal. The subsequent evolution of Trojan asteroids is the outcome of the joint action of different physical processes involving dynamical diffusion and excitation and collisional evolution. As a result, the present population is possibly different in both orbital and size distribution from the primordial one. No other significant population of Trojan asteroids have been found so far around other planets, apart from six Trojans of Mars, whose origin and evolution are probably very different from the Trojans of Jupiter.
