


|
|

|
Last time we gave a quick intro to the chemistry and thermodynamics we'll use to understand 'coupling'. Now let's really get started!
Suppose that we are in a setting in which some reaction
$$ \mathrm{X} + \mathrm{Y} \mathrel{\substack{\alpha_{\rightarrow} \\\longleftrightarrow\\ \alpha_{\leftarrow}}} \mathrm{XY} $$
takes place. Let's also assume we are interested in the production of \(\mathrm{XY}\) from \(\mathrm{X}\) and \(\mathrm{Y},\) but that in our system, the reverse reaction is favored to happen. This means that that reverse rate constant exceeds the forward one, let's say by a lot:
$$\alpha_\leftarrow \gg \alpha_\to$$
so that in equilibrium, the concentrations of the species will satisfy
$$\displaystyle{ \frac{[\mathrm{XY}]}{[\mathrm{X}][\mathrm{Y}]}\ll 1 }$$
which we assume undesirable. How can we influence this ratio to get a more desired outcome?
This is where coupling comes into play. Informally, we think of the coupling of two reactions as a process in which an endergonic reaction — one which does not 'want' to happen — is combined with an exergonic reaction — one that does 'want' to happen — in a way that improves the products-to-reactants concentrations ratio of the first reaction.
An important example of coupling, and one we will focus on, involves ATP hydrolysis:
$$ \mathrm{ATP} + \mathrm{H}_2\mathrm{O} \mathrel{\substack{\beta_{\rightarrow} \\\longleftrightarrow\\ \beta_{\leftarrow}}} \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} + \mathrm{H}^+ $$
where ATP (adenosine triphosphate) reacts with a water molecule. Typically, this reaction results in ADP (adenosine diphosphate), a phosphate ion \(\mathrm{P}_{\mathrm{i}}\) and a hydrogen ion \(\mathrm{H}^+\). To simplify calculations, we will replace the above equation with
$$\mathrm{ATP} \mathrel{\substack{\beta_{\rightarrow} \\\longleftrightarrow\\ \beta_{\leftarrow}}} \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} $$
since suppressing the bookkeeping of hydrogen and oxygen atoms in this manner will not affect our main points.
One reason ATP hydrolysis is good for coupling is that this reaction is strongly exergonic:
$$\beta_\to \gg \beta_\leftarrow$$
and in fact so much that
$$ \displaystyle{ \frac{\beta_\to}{\beta_\leftarrow} \gg \frac{\alpha_\leftarrow}{\alpha_\to} } $$
Yet this fact alone is insufficient to explain coupling!
To see why, suppose our system consists merely of the two reactions
$$ \begin{array}{ccc} \mathrm{X} + \mathrm{Y} & \mathrel{\substack{\alpha_{\rightarrow} \\\longleftrightarrow\\ \alpha_{\leftarrow}}} & \mathrm{XY} \\ \\ \mathrm{ATP} & \mathrel{\substack{\beta_{\rightarrow} \\\longleftrightarrow\\ \beta_{\leftarrow}}} & \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} \label{beta} \end{array} $$
happening in parallel. We can study the concentrations in equilibrium to see that one reaction has no influence on the other. Indeed, the rate equation for this reaction network is
$$ \begin{array}{ccl} \dot{[\mathrm{X}]} & = & -\alpha_\to [\mathrm{X}][\mathrm{Y}]+\alpha_\leftarrow [\mathrm{XY}]\\ \\ \dot{[\mathrm{Y}]} & = & -\alpha_\to [\mathrm{X}][\mathrm{Y}]+\alpha_\leftarrow [\mathrm{XY}]\\ \\ \dot{[\mathrm{XY}]} & = & \alpha_\to [\mathrm{X}][\mathrm{Y}]-\alpha_\leftarrow [\mathrm{XY}]\\ \\ \dot{[\mathrm{ATP}]} & =& -\beta_\to [\mathrm{ATP}]+\beta_\leftarrow [\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}]\\ \\ \dot{[\mathrm{ADP}]} & = &\beta_\to [\mathrm{ATP}]-\beta_\leftarrow [\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}]\\ \\ \dot{[\mathrm{P}_{\mathrm{i}}]} & = &\beta_\to [\mathrm{ATP}]-\beta_\leftarrow [\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}] \end{array} $$
When concentrations are constant, these are equivalent to the relations
$$\displaystyle{ \frac{[\mathrm{XY}]}{[\mathrm{X}][\mathrm{Y}]} = \frac{\alpha_\to}{\alpha_\leftarrow} \ \ \text{ and } \ \ \frac{[\mathrm{ADP}][\mathrm{P}_{\mathrm{i}}]}{[\mathrm{ATP}]} = \frac{\beta_\to}{\beta_\leftarrow} }$$
We thus see that ATP hydrolysis is in no way affecting the ratio of \([\mathrm{XY}]\) to \([\mathrm{X}][\mathrm{Y}].\) Intuitively, there is no coupling because the two reactions proceed independently. This 'independence' is clearly visible if we draw the reaction network as a so-called Petri net:
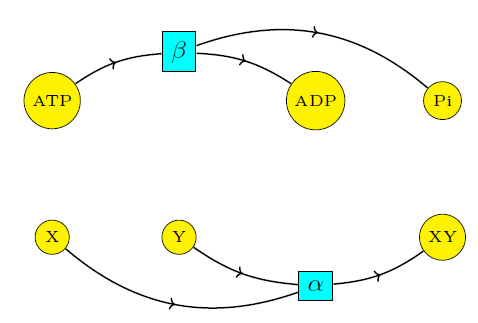
So what really happens when we are in the presence of coupling? Stay tuned for the next episode!
By the way, here's what ATP hydrolysis looks like in a bit more detail, from a website at Loreto College:
You can also read comments on Azimuth, and make your own comments or ask questions there!

|
|

|