

|
|
To wrap up this series, let's look at an even more elaborate cycle of reactions featuring emergent conservation laws: the citric acid cycle. Here's a picture of it from Stryer's textbook Biochemistry:
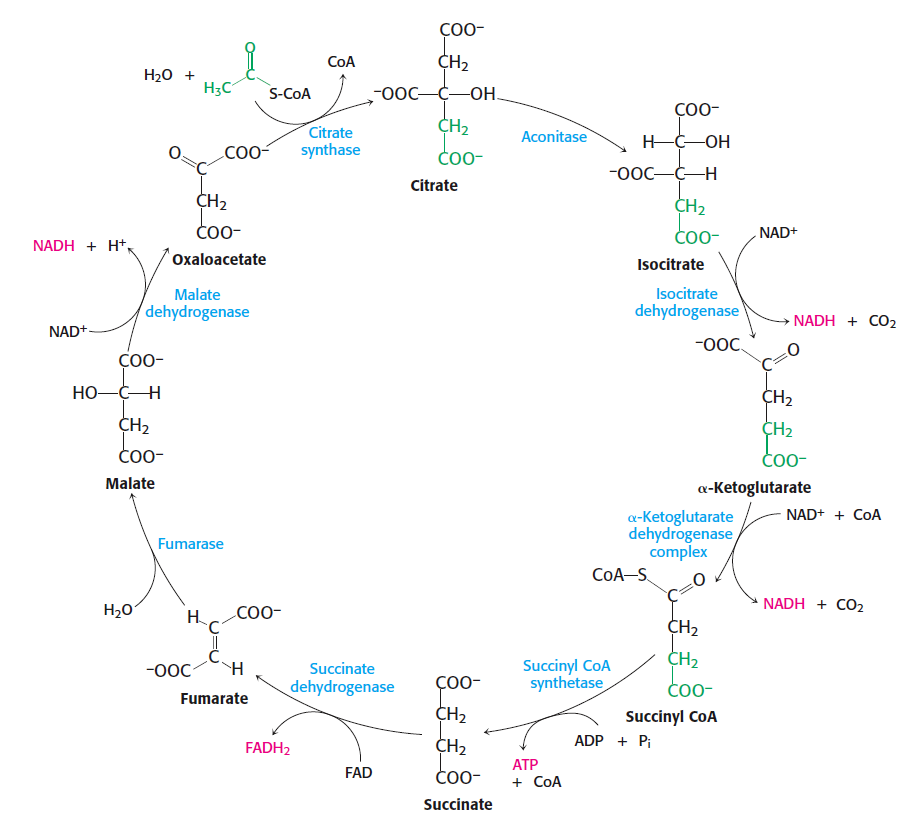
I'll warn you right now that we won't draw any grand conclusions from this example: that's why we left it out of our paper. Instead we'll leave you with some questions we don't know how to answer.
All known aerobic organisms use the citric cycle to convert energy derived from food into other useful forms. This cycle couples an exergonic reaction, the conversion of acetyl-CoA to CoA-SH, to endergonic reactions that produce ATP and a chemical called NADH.
The citric acid cycle can be described at various levels of detail, but at one level it consists of ten reactions:
$$\begin{array}{rcl} \mathrm{A}_1 + \text{acetyl-CoA} + \mathrm{H}_2\mathrm{O} & \longleftrightarrow & \mathrm{A}_2 + \text{CoA-SH} \\ \\ \mathrm{A}_2 & \longleftrightarrow & \mathrm{A}_3 + \mathrm{H}_2\mathrm{O} \\ \\ \mathrm{A}_3 + \mathrm{H}_2\mathrm{O} & \longleftrightarrow & \mathrm{A}_4 \\ \\ \mathrm{A}_4 + \mathrm{NAD}^+ & \longleftrightarrow & \mathrm{A}_5 + \mathrm{NADH} + \mathrm{H}^+ \\ \\ \mathrm{A}_5 + \mathrm{H}^+ & \longleftrightarrow & \mathrm{A}_6 + \textrm{CO}_2 \\ \\ \mathrm{A}_6 + \mathrm{NAD}^+ + \text{CoA-SH} & \longleftrightarrow & \mathrm{A}_7 + \mathrm{NADH} + \mathrm{H}^+ + \textrm{CO}_2 \\ \\ \mathrm{A}_7 + \mathrm{ADP} + \mathrm{P}_{\mathrm{i}} & \longleftrightarrow & \mathrm{A}_8 + \text{CoA-SH} + \mathrm{ATP} \\ \\ \mathrm{A}_8 + \mathrm{FAD} & \longleftrightarrow & \mathrm{A}_9 + \mathrm{FADH}_2 \\ \\ \mathrm{A}_9 + \mathrm{H}_2\mathrm{O} & \longleftrightarrow & \mathrm{A}_{10} \\ \\ \mathrm{A}_{10} + \mathrm{NAD}^+ & \longleftrightarrow & \mathrm{A}_1 + \mathrm{NADH} + \mathrm{H}^+ \end{array} $$
Here \(\mathrm{A}_1, \dots, \mathrm{A}_{10}\) are abbreviations for species that cycle around, each being transformed into the next. It doesn't really matter for what we'll be doing, but in case you're curious:
In reality, the citric acid cycle also involves inflows of reactants such as acetyl-CoA, which is produced by metabolism, as well as outflows of both useful products such as ADP and NADH and waste products such as CO2. Thus, a full analysis requires treating this cycle as an open chemical reaction network, where species flow in and out. However, we can gain some insight just by studying the emergent conservation laws present in this network, ignoring inflows and outflows — so let's do that!
There are a total of 22 species in the citric acid cycle. There are 10 forward reactions. We can see that their vectors are all linearly independent as follows. Since each reaction turns \(\mathrm{A}_i\) into \(\mathrm{A}_{i+1}\), where we count modulo 10, it is easy to see that any nine of the reaction vectors are linearly independent. Whichever one we choose to `close the cycle' could in theory be linearly dependent on the rest. However, it is easy to see that the vector for this reaction
$$\mathrm{A}_8 + \mathrm{FAD} \longleftrightarrow \mathrm{A}_9 + \mathrm{FADH}_2$$
is linearly independent from the rest, because only this one involves FAD. So, all 10 reaction vectors are linearly independent, and the stoichiometric subspace has dimension 10.
Since 22 - 10 = 12, there must be 12 linearly independent conserved quantities. Some of these conservation laws are 'fundamental', at least by the standards of chemistry. All the species involved are made of 6 different atoms (carbon, hydrogen, oxygen, nitrogen, phosphorus and sulfur), and conservation of charge provides another fundamental conserved quantity, for a total of 7.
(In our example from last time we didn't keep track of conservation of hydrogen and charge, because both \(\mathrm{H}^+\) and \(e^-\) ions are freely available in water... but we studied the citric acid cycle when we were younger, more energetic and less wise, so we kept careful track of hydrogen and charge, and made sure that all the reactions conserved these. So, we'll have 7 fundamental conserved quantities.)
For example, the conserved quantity
$$[\text{acetyl-CoA}] + [\text{CoA-SH}] + [\mathrm{A}_7]$$
arises from the fact that \(\text{acetyl-CoA}\), \(\text{CoA-SH}\) and \(\mathrm{A}_7\) contain a single sulfur atom, while none of the other species involved contain sulfur.
Similarly, the conserved quantity
$$3[\mathrm{ATP}] + 2[\mathrm{ADP}] + [\mathrm{P}_{\mathrm{i}}] + 2[\mathrm{FAD}] +2[\mathrm{FADH}_2]$$
expresses conservation of phosphorus.
Besides the 7 fundamental conserved quantities, there must also be 5 linearly independent emergent conserved quantities: that is, quantities that are not conserved in every possible chemical reaction, but remain constant in every reaction in the citric acid cycle. We can use these 5 quantities:
Of course, other conserved quantities can be formed as linear combinations of fundamental and emergent conserved quantities, often in nonobvious ways. An example is
$$3 [\text{acetyl-CoA}] + 3 [\mathrm{A}_2] + 3[\mathrm{A}_3] + 3[\mathrm{A}_4] + 2[\mathrm{A}_5] +$$ $$2[\mathrm{A}_6] + [\mathrm{A}_7] + [\mathrm{A}_8] + [\mathrm{A}_9] + [\mathrm{A}_{10}] + [\mathrm{NADH}]$$
which expresses the fact that in each turn of the citric acid cycle, one molecule of \(\text{acetyl-CoA}\) is destroyed and three of \(\mathrm{NADH}\) are formed. It is easier to check by hand that this quantity is conserved than to express it as an explicit linear combination of the 12 conserved quantities we have listed so far.
Finally, we bit you a fond farewell and leave you with this question: what exactly do the 7 emergent conservation laws do? In our previous two examples (ATP hydrolysis and the urea cycle) there were certain undesired reactions involving just the species we listed which were forbidden by the emergent conservation laws. In this case I don't see any of those. But there are other important processes, involving additional species, that are forbidden. For example, if you let acetyl-CoA sit in water it will 'hydrolyze' as follows:
$$\text{acetyl-CoA} + \mathrm{H}_2\mathrm{O} \longleftrightarrow \text{CoA-SH} + \text{acetate} + \text{H}^+$$
So, it's turning into CoA-SH and some other stuff, somewhat as does in the citric acid cycle, but in a way that doesn't do anything 'useful': no ATP or NADH is created in this process. This is one of the things the citric acid cycle tries to prevent.
(Remember, a reaction being 'forbidden by emergent conservation laws' doesn't mean it's absolutely forbidden. It just means that it happens much more slowly than the catalyzed reactions we are listing in our reaction network.)
Unfortunately acetate and \(\text{H}^+\) aren't on the list of species we're considering. We could add them. If we added them, and perhaps other species, could we get a setup where every emergent conservation law could be seen as preventing a specific unwanted reaction that's chemically allowed?
Ideally the dimension of the space of emergent conservation laws would match the dimension of the space spanned by reaction vectors of unwanted reactions, so 'everything would be accounted for'. But even in the simpler example of the urea cycle, we didn't achieve this perfect match.
You can also read comments on Azimuth, and make your own comments or ask questions there!

|
|