


|
|

|
There's a lot more to network theory than this. But before I dive into the next big topic, I want to mention a few more odds and ends about Petri nets and reaction networks. For example, their connection to logic and computation!
As we've seen, a stochastic Petri net can be used to describe a bunch of chemical reactions with certain reaction rates. We could try to use these reactions to build a 'chemical computer'. But how powerful can such a computer be?
I don't know the answer. But before people got interested in stochastic Petri nets, computer scientists spent quite some time studying plain old Petri nets, which don't include the information about reaction rates. They used these as simple models of computation. And since computer scientists like to know which questions are decidable by means of an algorithm and which aren't, they proved some interesting theorems about decidability for Petri nets.
Let me talk about: 'reachability': the question of which collections of molecules can turn into which other collections, given a fixed set of chemical reactions. For example, suppose you have these chemical reactions:
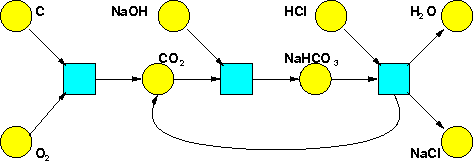
C + O2 → CO2
CO2 + NaOH → NaHCO3
NaHCO3 + HCl → H2O + NaCl + CO2
Can you use these to turn
into
It's not too hard to settle this particular question—we'll do it soon. But settling all possible such questions turns out to be very hard
Remember:
Definition. A Petri net consists of a set $S$ of species and a set $T$ of transitions, together with a function
$i : S \times T \to \mathbb{N} $
saying how many copies of each state shows up as input for each transition, and a function
$o: S \times T \to \mathbb{N}$
saying how many times it shows up as output.
Today we'll assume both $S$ and $T$ are finite.
Jacob and I like to draw the species as yellow circles and the transitions as aqua boxes, in a charmingly garish color scheme chosen by Dave Tweed. So, the chemical reactions I mentioned before:
C + O2 → CO2
CO2 + NaOH → NaHCO3
NaHCO3 + HCl → H2O + NaCl + CO2
give this Petri net:
A 'complex' is, roughly, a way of putting dots in the yellow circles. In chemistry this says how many molecules we have of each kind. Here's an example:

This complex happens to have just zero or one dot in each circle, but that's not required: we could have any number of dots in each circle. So, mathematically, a complex is a finite linear combination of species, with natural numbers as coefficients. In other words, it's an element of $\mathbb{N}^S.$ In this particular example it's
Given two complexes, we say one is reachable from another if, loosely speaking, we can get to it from the other by a finite sequence of transitions. For example, earlier on I asked if we can get from the complex I just mentioned to the complex
which we can draw like this:

And the answer is yes, we can do it with this sequence of transitions:




This settles the question I asked earlier.
So in chemistry, reachability is all about whether it's possible to use certain chemical reactions to turn one collection of molecules into another using a certain set of reactions. I hope this is clear enough; I could formalize it further but it seems unnecessary. If you have questions, ask me or read this:
Now the reachability problem asks: given a Petri net and two complexes, is one reachable from the other?
If the answer is 'yes', of course you can show that by an exhaustive search of all possibilities. But if the answer is 'no', how can you be sure? It's not obvious, in general. Back in the 1970's, computer scientists felt this problem should be decidable by some algorithm... but they had a lot of trouble finding such an algorithm.
In 1976, Roger J. Lipton showed that if such an algorithm existed, it would need to take at least an exponential amount of memory space and an exponential amount of time to run:
This means that most computer scientists would consider any algorithm to solve the reachability problem 'infeasible', since they like polynomial time algorithms.
On the bright side, it means that Petri nets might be fairly powerful when viewed as computers themselves! After all, for a universal Turing machine, the analogue of the reachability problem is undecidable. So if the reachability problem for Petri nets were decidable, they couldn't be universal computers. But if it were decidable but hard, Petri nets might be fairly powerful—though still not universal—computers.
In 1977, at the ACM Symposium on the Theory of Computing, two researchers presented a proof that reachability problem was decidable:
However, it turned out to be flawed! I read about this episode here:
This is a very nice introduction to early work on Petri nets and decidability. Peterson had an interesting idea, too:
There would seem to be a very useful connection between Petri nets and Presburger arithmetic.
He gave some evidence, and suggested using this to settle the decidability of the reachability problem. I found that intriguing! Let me explain why.
Presburger arithmetic is a simple set of axioms for the arithmetic of natural numbers, much weaker than Peano arithmetic or even Robinson arithmetic. Unlike those other systems, Presburger arithmetic doesn't mention multiplication. And unlike those other systems, you can write an algorithm that decides whether any given statement in Presburger arithmetic is provable.
However, any such algorithm must be very slow! In 1974, Fischer and Rabin showed that any decision algorithm for Presburger arithmetic has a worst-case runtime of at least
$$2^{2^{c n}}$$
for some constant $c$, where $n$ is the length of the statement. So we say the complexity is at least doubly exponential. That's much worse than exponential! On the other hand, an algorithm with a triply exponential run time was found by Oppen in 1978.
I hope you see why this is intriguing. Provability is a lot like reachability, since in a proof you're trying to reach the conclusion starting from the assumptions using certain rules. Like Presburger arithmetic, Petri nets are all about addition, since they consists of transitions going between linear combinations like this:
That's why the old literature calls Petri nets vector addition systems. And finally, the difficulty of deciding provability in Presburger arithmetic smells a bit like the difficulty of deciding reachability in Petri nets.
So, I was eager to learn what happened after Peterson wrote his book.
For starters, in 1981, the very year Peterson's book came out, Ernst Mayr showed that the reachability problem for Petri nets is decidable:
As you can see from the title, Mayr actually proved some other property was decidable. However, it follows that reachability is decidable, and Mayr pointed this out in his paper. In fact the decidability of reachability for Petri nets is equivalent to lots of other interesting questions. You can see a bunch here:
Mayr's algorithm was complicated. Worse still, it seems to take a hugely long time to run. The best known upper bound on its runtime is a function that's not even primitive recursive! Typical functions of this sort are the Ackermann function and the closely related Ackermann numbers. If you don't know about those, now is the time to learn.
Remember that we can define multiplication by iterating addition:
$$n \times m = n + n + n + \cdots + n$$where add $n$ to itself $m$ times. Then we can define exponentiation by iterating multiplication:
$$ n \uparrow m = n \times n \times n \times \cdots \times n$$where we multiply $n$ by itself $m$ times. Here I'm using Knuth's up-arrow notation. Then we can define tetration by iterating exponentiation:
$$n \uparrow^2 m = n \uparrow (n \uparrow (n \uparrow \cdots \uparrow n)))$$Then we can define an operation $\uparrow^3$ by iterating tetration, and so on. All these functions are primitive recursive. But the $n$th Ackermann number is not; it's defined to be
$$n \uparrow^n n$$This grows at an insanely rapid rate:
$$1 \uparrow 1 = 1$$ $$2 \uparrow^2 2 = 4 $$ $$3 \uparrow^3 3 = 3^{3^{3^{.^{.^{.}}}}}$$where we have a stack of $3^{3^3}$ threes—or in other words, $3^{7625597484987}$ threes! When we get to $4 \uparrow^4 4,$ my mind boggles. I wish it didn't, but it does.
Luckily, in 1998 someone came up with a faster algorithm:
He showed this algorithm is doubly exponential in space and time. That's very slow, but not insanely slow.
So: if I tell you some chemicals and a bunch of reactions involving these chemicals, you can decide when some combination of these chemicals can turn into another combination. But it may take a long time to decide this. And we don't know exactly how long: somewhere between 'exponentially long' and 'doubly exponentially long'.
What about the connection to Presburger arithmetic? This title suggests that it exists:
But I don't understand the paper well enough to be sure. Can someone say more?
Also, does anyone know more about the computational power of Petri nets? They're not universal computers, but is there a good way to say how powerful they are? Does the fact that it takes a long time to settle the reachability question really imply that they have a lot of computational power?
Next let me explain the secret reason I'm so fascinated by this. This section is mainly for people who like category theory.
As I mentioned once before, a Petri net is actually nothing but a presentation of a symmetric monoidal category that's free on some set of objects and some set of morphisms going between tensor products of those objects:
In chemistry we write the tensor product additively, but we could also write it as $\otimes$. Then the reachability problem consists of questions of this general type:
Suppose we have a symmetric monoidal category freely generated by objects $A, B, C$ and morphisms $$e: A \to B \otimes C $$ $$f: A \otimes A \otimes B \to A \otimes C$$ $$g: A \otimes B \otimes C \to A \otimes B \otimes B$$ $$h : B \otimes A \otimes A \to B$$Is there a morphism from $B \otimes A \otimes A$ to $A \otimes A$?
This is reminiscent of the word problem for groups and other problems where we are given a presentation of an algebraic structure and have to decide if two elements are equal... but now, instead of asking whether two elements are equal we are asking if there is a morphism from one object to another. So, it is fascinating that this problem is decidable—unlike the word problem for groups—but still very hard to decide.
Just in case you want to see a more formal statement, let me finish off by giving you that:
Reachability problem. Given a symmetric monoidal category $C$ freely generated by a finite set of objects and a finite set of morphisms between tensor products of these objects, and given two objects $x,y \in C,$ is there a morphism $f: x \to y$?
Theorem (Lipton, Mayr). There is an algorithm that decides the reachability problem. However, for any such algorithm, for any $c > 0,$ the worst-case run-time exceeds $2^{c n}$ where $n$ is the size of the problem: the sum of the number of generating objects, the number of factors in the sources and targets of all the generating morphisms, and the number of factors in the objects $x,y \in C$ for which the reachability problem is posed.
You can also read comments on Azimuth, and make your own comments or ask questions there!

|
|

|