


|
|

|
Now I'd like to say a bit about what this does for us. In particular, how it relates 11-dimensional supergravity to the game of billiards!
I would also like to explain in vivid detail what the Cayley integers and the action of \(\mathrm{PSL}_2(\mathbf{O})\) 'look like' — along with some lower-dimensional examples that arise from other kinds of integers inside the real numbers, complex numbers and quaternions. That would force me to learn some interesting things. But I think it's better to start by zipping through the big picture, and then returning to details later if I have time.
The basic idea is this.
Suppose you follow a solution of general relativity like our universe back toward the Big Bang. Then under certain conditions, each little piece of space 'decouples' from the rest as we go back. This means that in the limit, as you go back toward the Big Bang, the complicated nonlinear partial differential equations describing general relativity reduce to ordinary differential equations for the metric at each point in space.
Even better, as we go back in time, these equations reduce to equations just like those describing a Newtonian point particle bouncing around inside a region of higher-dimensional hyperbolic space! It's like a higher-dimensional version of an idealized frictionless billiard ball bouncing endlessly between the walls of a billiard table:

The table pictured here, with straight walls capped off by semicircles, is known to give chaos if it's is long enough. That is, the future position of the billiard ball depends in a very sensitive way on its initial position and velocity. Tiny changes in initial conditions produce bigger and bigger changes in the ball's position each time the ball crosses the table, making it impractical to predict what will happen in the far future.
Mathematical physicists have thought a lot about what happens with different kinds of billiard table, including higher-dimensional tables and tables that are curved Riemannian manifolds, with or without a boundary. As you might expect, nearby trajectories tend to drift far apart on manifolds with negative curvature, like hyperbolic space. So, it's believed that extrapolating general relativity back to the Big Bang gives chaos in many cases!
There are some obvious questions you should be wondering about.
For example: an idealized frictionless billiard ball can bounce around endlessly on a table. I'm using that fact when I say it's "impractical to predict what will happen in the far future." But you only need to go back in time a finite amount before you reach the Big Bang. So, how can these two problems be isomorphic?
The answer is interesting: we need to take the logarithm of time in the Big Bang problem to make it isomorphic to the billiard ball problem! As \(t \to 0\), its logarithm goes all the way down to \(-\infty\). So the universe bounces around infinitely many times, changing shape chaotically faster and faster, as we go back toward the Big Bang.
The idea here goes back to some Russians including Evgeny Lifshitz, famous for the series of physics textbooks everyone calls 'Landau and Lifshitz':
so the phenomenon I'm talking about is called a 'BKL singularity'. You can read more about it here:
To clarify a bit, I should add that the model of a billiard ball reflecting off hard walls only shows up as a limiting case. At first the walls are 'soft': we have a ball moving around in a smooth potential. But as we go back in time they become 'harder', or steeper.
Also, I should emphasize that this picture is thoroughly worked out only for cosmologies where space at any given time is homogeneous but non-isotropic — especially the so-called 'Bianchi IX models'. This phrase refers to a classification of 3-dimensional real Lie algebras into nine families, which also gives a classification of spatially homogeneous cosmologies.
In the real world, we can expect space to be not quite homogeneous, and then to argue for the significance of the BKL singularity we need to argue that different small patches of space decouple from each as \(t \to 0\). I'm not sure how solid this argument is. But of course, if we get serious about the \(t \to 0\) limit we need to think about quantum gravity, including various forms of matter...
But perhaps I should make it clear: I'm in this for the beautiful math. I don't care if this stuff is relevant to the real world. But it's still nice to use physics ideas in the quest for beautiful math.
And if we do, it naturally leads us to think about cosmological billiards when space is not 3-dimensional but has other dimensions. And then a nice 'dictionary' shows up relating some of these possibilities and billiard balls bouncing around in regions of hyperbolic spaces of different dimensions.
In this dictionary, if spacetime is \(n\)-dimensional and there are \(d\) 'dilaton fields' in our gravity theory, we get a billiard ball bouncing around in a region of \((n+d-2)\)-dimensional hyperbolic space. Depending on other details, this region in hyperbolic space could have finite or infinite volume:
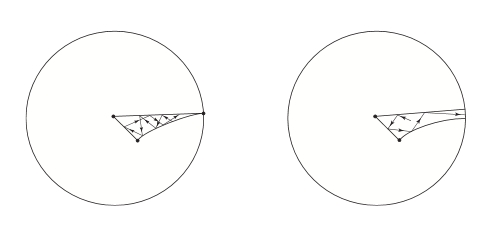
The first case gives chaotic motion; in the second, the billiard typically bounces around a bit and then shoots off to infinity. (I got this picture from here.)
And in the nicest cases, this region is a fundamental domain of a Coxeter group acting on hyperbolic space!
For example, the original case studied by Belinskii, Khalatnikov and Lifshitz was pure gravity without matter in 4d spacetime. This means \(n = 4\) and \(d = 0\): no dilatons. This gives us billiards moving around in a region of the hyperbolic plane. And with a lot more work, you can show this region looks like any one of the triangles here:
These triangles are fundamental domains for a group called the \((2,3,\infty)\) triangle group. For any natural numbers \(p,q,r\), the (p,q,r) triangle group has generators \(s_1, s_2, s_3\) obeying relations
$$ s_1^2 = s_2^2 = s_3^2 = 1 $$
$$ (s_1 s_2)^p = (s_2 s_3)^q = (s_3 s_1)^r $$
This group is a simple example of a Coxeter group. If
$$ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} < 1 $$
it acts on the hyperbolic plane, with each generator acting as a reflection across a line. This group action has fundamental domains that are triangles with interior angles \(\pi/p, \pi/q, \pi/r\). For example, the \((2,3,7)\) triangle group, studied by Hermann Weyl, has fundamental domains like this:
If \(p,q\) or \(r\) become infinite, we don't technically have a Coxeter group, but we still get a group by dropping the relation containing that number. And the group still acts on the hyperbolic plane... but some of the corners of the triangles move off to infinity — that is, the edge of the disc above. An extreme case is the \((\infty,\infty,\infty)\) triangle group, which gives this:
The \((2,3,\infty)\) triangle group, coming from gravity without matter in 4d spacetime, is not so extreme: each triangle has just one vertex at infinity. We can write down a Coxeter diagram for it if we generalize these diagrams a bit and let ourselves label one edge by infinity:
_coxeter_diagram.jpg)
And this group is very important: it's none other than \(\mathrm{PGL}(2,\mathbb{Z})\). So its even part — the part generated by pairs of reflections — is the modular group \(\mathrm{PSL}(2,\mathbb{Z})\).
There are lots of other fun examples. But let me jump to the punchline: what does this dictionary relating gravity theories and billiards say about the mathematically most exciting gravity theory: 11-dimensional supergravity, with \(n = 11\) and \(d = 0\)? If we look at the simplest purely bosonic solutions, we get a billiard ball bouncing around in a region of 9-dimensional hyperbolic space. And this region is just the fundamental domain of the Coxeter group I described last time: \(\mathrm{E}_{10}\)!
Remember, this group is generated by 10 reflections in 9-dimensional hyperbolic space. Each reflection gives a wall of our billiard ball table. And the even part of this group — the part generated by pairs of reflections, giving orientation-preserving transformations — is none other than \(\mathrm{PSL}(2,\mathbf{O})\), where \(\mathbf{O}\) is the Cayley integers!
To learn more, I recommend this paper:
or for something much more gentle, this:
There is much more to say... most of which I don't know. So next time I'll come down to earth a bit and start describing the Cayley integers in detail. One doesn't need to know fancy physics or group theory to understand and enjoy them. You really just need to know how to add, subtract, multiply, divide... and think about shapes in 8 dimensions.

|
|

|