


|
|

|
is that it gives us two ways to think about the symmetry group of the hyperbolic plane. On the one hand, it consists of fractional linear transformations with real entries:
$$ z \mapsto \frac{a z + b}{c z + d} \quad a,b,c,d\in \mathbb{R} $$acting on the upper half-plane in \(\mathbb{C}\), which is one way to think about the hyperbolic plane. On the other hand, it's the identity component of the Lorentz group of 3d spacetime, acting on the hyperboloid
$$ \{(t,x,y) \in \mathbb{R}^{3} : t^2 - x^2 - y^2 = 1 , t > 0\} $$which is another way to think about the hyperbolic plane.
But the really great thing is that because the field \(\mathbb{R}\) contains the integers as a discrete subring, \(\mathrm{PSL}(2,\mathbb{R})\) contains the modular group \(\mathrm{PSL}(2,\mathbb{Z})\) as a discrete subgroup, acting on the hyperbolic plane with fundamental domains like this:
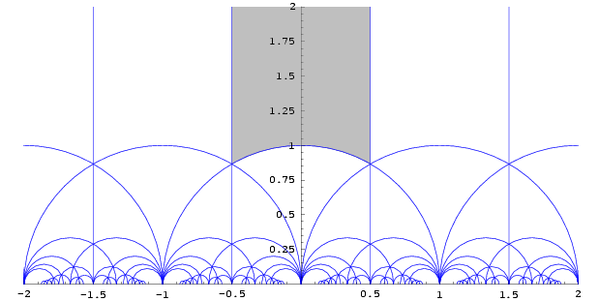
This connects the Lorentz group of 3d spacetime to number theory... thanks to things like the theory of modular forms. Part of the point is that \(\mathrm{PSL}(2,\mathbb{Z})\) is not just a discrete subgroup of \(\mathrm{PSL}(2,\mathbb{R})\). It's an arithmetic group! Very very roughly, this is like an algebraic group, but defined using some ring resembling the integers, rather than a field.
And here is where a further marvelous fact comes into play. The algebra of octonions \(\mathbb{O}\) contains a (nonassociative!) discrete subring \(\mathbf{O}\), sometimes called the Cayley integers, Coxeter integers, or octavians. If you ignore the fact that you can multiply octonions, you can think of the octonions as forming an 8-dimensional real inner product space... and then the Cayley integers form a lattice in this vector space, which is, up to a rescaling, nothing other than the \(\mathrm{E}_8\) root lattice!
So, each Cayley integer has 240 nearest neighbors, arranged in a pattern like this:

which you should imagine in 8 dimensions.
That's already great. But the Cayley integers are closed under multiplication, and this makes even more magic happen!
For example, it lets us define an arithmetic subgroup \(\mathrm{PSL}(2,\mathbf{O})\) of the group
$$ \mathrm{PSL}(2,\mathbb{O}) \cong \mathrm{SO}_0(9,1) $$This acts on the 9-dimensional hyperbolic space
$$ \{x \in \mathbb{R}^{10} :\; x_0^2 - x_1^2 - \cdots - x_9^2 = 1 , \; x_0 > 0\} $$Even better, this marvelous discrete group acting on 9d hyperbolic space is related to \(\mathrm{E}_8\). In fact, \(\mathrm{PSL}(2,\mathbf{O})\) is the even part of the Coxeter group \(\mathrm{E}_{10}\), which arises from a Coxeter diagram like that of \(\mathrm{E}_8\), but longer:
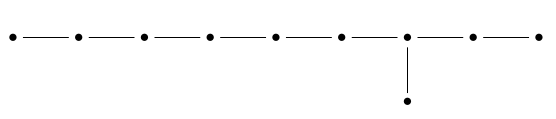
This group has one generator \(s_i\) for each dot, with relations $$ s_i^2 = 1 $$ for each dot, $$ s_i s_j s_i = s_j s_i s_j $$ for any pair of dots connected by an edge, and $$ s_i s_j = s_j s_i $$ for pairs not connected by an edge. Each of these generators acts as reflection across a hyperplane in 9-dimensional hyperbolic space. So, it's called a hyperbolic Coxeter group. The subgroup generated by products of two generators is called the even part of this group, and it's the same as \(\mathrm{PSL}_2(\mathbf{O})\).
The same thing happens in a much simpler way for \(\mathrm{PSL}_2(\mathbb{Z})\): it's the even part of a hyperbolic Coxeter group acting on the hyperbolic plane with fundamental domains like this:
_tiling.png)
You get these by taking fundamental domains for \(\mathrm{PSL}_2(\mathbb{Z})\), which I showed you before in the upper half-plane, and chopping them in half.
So, thanks to Cayley integers, we know there is a similar but much more glorious picture in 9-dimensional hyperbolic space! Unfortunately this blog is too low-dimensional to contain it.
This Coxeter diagram:

can also be seen as a Dynkin diagram — of a dangerously big kind, since it gives an infinite-dimensional Lie algebra, a hyperbolic Kac–Moody algebra. This Lie algebra also goes by the name of \(\mathrm{E}_{10}\), and it's closely related to the Coxeter group I just described: the Coxeter group is the Weyl group of the Lie algebra.
The Lie algebra \(\mathrm{E}_{10}\) has tantalizing and mysterious connections to physics. Ideally, I would explain something about them in this series. At the very least, I want to say how hyperbolic Coxeter groups like \(\mathrm{E}_{10}\) are related to supersymmetric quantum cosmological billiard balls! But the paper I want to recommend to you today:
has somewhat less cosmic goals, so it's a good place to start. It describes how the isomorphisms
$$ \begin{array}{ccl} \mathrm{PSL}(2,\mathbb{R})& \cong &\mathrm{SO}_0(2,1) \\ \mathrm{PSL}(2,\mathbb{C})& \cong &\mathrm{SO}_0(3,1) \\ \mathrm{PSL}(2,\mathbb{H})& \cong &\mathrm{SO}_0(5,1) \\ \mathrm{PSL}(2,\mathbb{O})& \cong &\mathrm{SO}_0(9,1) . \end{array} $$work, with an emphasis on the subtleties introduced by noncommutativity (for the quaternions \(\mathbb{H}\) and octonions \(\mathbb{O}\)) and nonassociativity (for \(\mathbb{O}\)). It describes various subrings of 'integers' in \(\mathbb{R}, \mathbb{C}, \mathbb{H}\) and \(\mathbb{O}\) and how these give rise to arithmetic groups. And, it describes how these are related to hyperbolic Coxeter groups. This is tremendously pretty math even if you don't care about the potential applications to (fun, far-out, highly theoretical, not-yet-experimentally-testable) physics.

|
|

|