Michael Weiss: Hmm, homework  Schmotons  John Baez: A Six-Step

John Baez: A Gaussian Bump

Let me sketch step 1 here and see if I can get Michael to do the actual work.

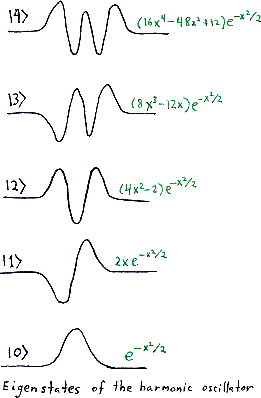
We can think of states of the harmonic oscillator as wavefunctions, complex functions on the line, but they have a basis given by eigenstates of the harmonic oscillator Hamiltonian H. We call these states | n> where n = 0,1,2,3, etc., and we have

H |n> = (n + 1/2) |n>

As wavefunctions, |0> is a Gaussian bump centered at the origin. This is the ``ground state'' of the harmonic oscillator, the state with least energy. The state |n> is the same Gaussian bump times a polynomial of degree n, giving a function whose graph crosses the x axis n times:

We can think of |n> as a state with n ``quanta'' in it. Quanta of what? Quanta of energy! This is a little weird, but it'll come in handy to think of this way later. By the time we get to step 6, these ``quanta'' will be honest-to-goodness photons.

So it's nice to have operators that create and destroy quanta. We'll use the usual annihilation operator a and creation operator a^*,  given by

a |n> = sqrt(n) |n-1>

and

a^* |n> = sqrt(n+1) |n+1>

One can relate these guys to the momentum and position operators p and q, which act on wavefunctions as follows:

p = -i (d/dx)

q = x

In the latter equation I really mean ``q is multiplication by the function x''; these equations make sense if you apply both sides to some wavefunction.

So maybe Michael can remember or figure out the formulas relating the p's and q's to the a's and a^*'s.

Once we have those, there's something fun we can do.

To translate a wavefunction psi to the right by some amount c, all we need to do is apply the operator

e^-icp

to it. The reason is that

((d/dc) e^-icp psi) (x) = (-ip e^-icp psi) (x)

=  -((d/dx) e^-icp psi) (x)

so the rate at which e^-icp psi changes as we change c is really just minus the derivative of that function...meaning that it's getting translated over to the right. (We'll give some more detail for this step at the end of this section.) Folks say that the momentum operator p is the ``generator of translations'':

So we can get a wavefunction that's a Gaussian bump centered at the point x = c by taking our ground state |0> and translating it, getting:

e^-icp|0>

This is called a ``coherent state''. In some sense it's the best quantum approximation to a classical state of the harmonic oscillator where the momentum is zero and the position is c. (We can make this more precise later if desired.)

If we express p in terms of a and a^*, and write

e^-icp = 1 - icp + ((icp)²/2!) + ...

we can expand our coherent state in terms of the eigenstates |n>. What does it look like?

If we figure this out, we can see what is the expected number of ``quanta'' in the coherent state. And this will eventually let us figure out the expected number of photons in a coherent state of the electromagnetic field: for example, a state which is the best quantum approximation to a plane wave solution of the classical Maxwell equations. It looks like there should should be about c<sup>2</sup> ``quanta'' in the coherent state e^-icp|0>. This should shed some more light (pardon the pun) on why our previous computations gave a photon density proportional to the amplitude squared and thus the energy density.

The thing to understand is why, even when we have a whole bunch of photons presumably in phase and adding up to a monochromatic beam of light, the amplitude is only proportional to the square root of the photon number. You could easily imagine that a bunch of photons completely randomly out of phase would give an average amplitude proportional to the square root of the photon number, just as |heads - tails| grows on average like the number of coins tossed (for a fair coin).

A few more details:

Suppose we have a wavefunction psi. What is e^-icp psi? The answer is: it's just psi translated c units to the right.

Why? If we take psi and translate it c units to the right we get

psi(x - c)

so we need to show that

(e^-icp psi)(x) = psi(x - c).

To show this, first note that it's obviously true when c = 0. Then take the derivative of both sides as a function of c and note that they are equal. That does the job.

We are assuming that if two differentiable functions are equal somewhere and their derivatives agree everywhere, then they can't ``start being different'', so they must be equal everywhere.

Or if that sounds too vague:

Technically, we are just using the fundamental theorem of calculus. Say we have two differentiable functions f(s) and g(s). Then

f(x) = f(0) + integral₀^x  f'(s) ds

It follows from this that if f(0) = g(0) and f'(s) = g'(s) for all s, then f(x) = g(x) for all x.

3/10/1998