John Baez assigns:
So maybe Michael can remember or figure out the formulas relating the p's and q's to the a's and a*'s.Hey, I know that! Basic QM...just toss off the answer, q+ip, q-ip,...No, wait, what does it say here: ``Show all work!!''
All righty, then. Actually this is kind of fun. I still remember how slick and utterly unintuitive this seemed when I first encountered it in Dirac's book.
Moreover, this slick calculation evokes even earlier memories, of two jewels of high-school algebra: (a+b)(a-b) = a2-b2, and (a+bi)(a-bi) = a2+b2. If these have lost their luster over the years, try them out on your favorite bright 8-year old. I think of (a+b)(a-b) as the primordial instance of that staple of mathematical physics: cancellation of terms, leaving a simple final result.
Well, if having the cross-term cancel is cool, having them not cancel turns out to be even cooler!
Dirac does offer one slender reed of motivation, a single sentence: ``The above equations are all as in the classical theory.'' The ultimate incarnation of Bohr's correspondence principle. In fact, Olivier Darrigol wrote a book about that a few years back:
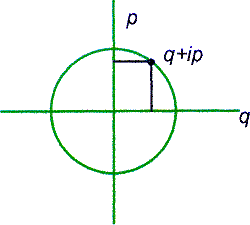
From C-Numbers to Q-Numbers: The Classical Analogy in the History of Quantum Theory. California Studies in the History of Science, University of California Press, December 1992.OK, so let's start with a classical dot racing around in a circle. Projecting onto the x-axis gives simple harmonic motion. We'll use q for the x-coordinate and p for the y-coordinate, following Hamiltonian tradition. (Why p's and q's? Because Hamilton hung out in Irish pubs, minding his pints and quarts?)
Now as complex number, q+ip is that racing dot. Everything flows from q+ip. Let me be ruthless with factors of m and the spring constant and the like-- set them all to 1. The total energy is H=(q2+p2)/2, or (1/2)(q+ip)(q-ip). As a function of time, q+ip = e-it (for clockwise motion). The velocity vector is -i(q+ip).
OK, so let's do the same thing in Quantum Land. Now q and p no longer commute; in fact, qp-pq = i. So we set Z=q+ip and try to compute H, which was ZZ*/2 last time. But this time the cross-terms don't cancel, and we get:
I guess I won't go through the whole development. To get the annihilation operator a and the creation operator a*, we just need to absorb that pesky factor of 2 into a and a*: a = Z/sqrt(2), a* = Z*/sqrt(2). [Sqrt(2) will be turning up a lot in these notes, so for the HTML version I will use the abbreviation sq2. --ed.] So we get:
I think that will do it for HW, part 1.
Hmmm. John Baez promised that the plain old harmonic oscillator would have something to do with E and B. Hey wait, the energy for the harmonic oscillator is (p2 + q2)/2; for the electromagnetic field, (E2 + B2)/2. Coincidence? You be the judge.
OK, part 2 of the homework. First John Baez defines a coherent state to be e-ipc|0>, then asks:
If we express p in terms of a and a*, and writeSince p = (a-a*)/i sq2, -ipc = -c(a-a*)/ sq2. Let's write D for c/sq2, so -ipc = -D(a-a*). So our coherent state is:e-ipc = 1 - ipc + ((ipc)2/2!) + ... we can expand our coherent state in terms of the eigenstates |n>. What does it look like?
The problem is to figure out the coefficient of |n> , i.e., express the coherent state in the form:
[At this point, the poor student went off on a long detour. Inspired by John Baez's remarks about coin-tossing, he rambled through the theory of random walks-- at random! Alas, this lead nowhere, but (by a process to tortuous to summarize) it did inspire his next step. --ed.]
So I guessed that
so of course
Hmmm. Let's use this guess for the Cn, and apply a to SUMn Cn |n>; to make things a little simpler, let's divide through by C0 first. We get:
I.e., the coherent state would be an eigenstate of the annihilation operator a!
So I tried to prove this with combinatorial tricks, but no luck. Then I had the idea of going back to using q and p, instead of a and a*. With hindsight, the suggestion to rewrite 1 - ipc + ((ipc)2/2!) - ... in terms of a and a* looks like a false lead. Say it ain't so, John!
So here's how my solution goes: [slicker solutions will be found later in these notes. --ed.]
First off, we need a generalization of [q,p] = i. Here it is:
which allows us to move q's past p's.
Next we apply this rule to q e-ipc [You'll find the two lines of computation in the postscript version, but I'm not up to translating them into HTML. --ed.]
or q e-ipc = e-ipc q + c e-ipc. So:
since q+ip does annihilate |0>. So e-ipc|0> is an eigenstate of a, with eigenvalue c/ sq2 (=D).
And now for the payoff!
If the coherent state is proportional to:
then the probability distribution over the energy eigenstates is:
The expectation value for this Poisson distribution is D2. In other words, the average number of photons--err, quanta-- in the coherent state is D2.
Hmm, Baez has already pointed out how the coherent state looks like a bump displaced c units from the origin.
Suddenly the ``classical dot'' racing in a circle has a whole new lease on life. There was something pretty unsavory about what Dirac did to it. It reminds me of those ``before and after'' pictures-- are they really the same person? Before: the dot races in a circle of any radius. After: nothing races around at all, instead we have a bunch of wavefunctions that just sit there. Yeah, I know-- only after we've factored out the time-dependent part e-i(n+1/2)t. But this kind of motion is in an imaginary direction, and doesn't affect the wherabouts of the particle, if you know what I mean.
Could these utterly different kinematics really come from the same cinematographer?
Sure! Just use coherent states. As D increases continuously, the average energy increases continuously, as does the range of motion of the bump.
Hmm. Guess I should check that last assertion.
Hokay, we want the time evolution of the bump. Should be a piece of cake. The time evolution of |n> is just e-i(n+1/2)t |n>, and we've expressed the coherent state as a sum of energy eigenstates.
Let's redefine the zero-point of energy to get rid of that annoying 1/2. So e-iHte-ipc|0> is equal to C0 times:
that is, exp(-ip e-itc)|0>, since basically we've just replaced D with e-itD, and c with e-itc. (The argument above didn't actually use the assumption that c was real anywhere.)
Hmmm. A bump that swang back and forth harmonically would look like this: exp(-ip( cos t) c)|0>. How to relate this to exp(-ip e-itc)|0>?
Aha! Euler to the rescue: e-it = cos t - i sin t. Uh-oh, now we've got e-ip ( cos t) c e-p ( sin t)c |0>.
What does e-p ( sin t)c |0> look like?
Help!