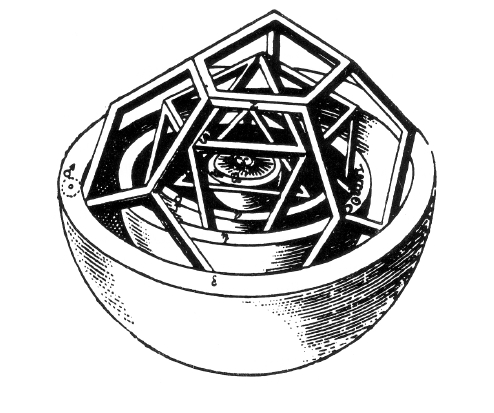
From Kepler's Mysterium Cosmographicium,
in which he modeled the orbits of the five known planets using Platonic solids.
The cube fits outside all those shown above.
What's the pattern in this sequence?
In 2 dimensions, the most symmetrical polygons of all are the 'regular polygons'. All the edges of a regular polygon are the same length, and all the angles are equal. If you only count the convex ones, it's easy to list all the regular polygons: the equilateral triangle, the square, the regular pentagon, and so on. In short, there is an infinity of regular polygons: one with n sides for each n > 3. (The cases n = 0,1, and 2 are bit degenerate.)
In 3 dimensions, the most symmetrical polyhedra of all are the 'regular polyhedra', also known as the 'Platonic solids'. All the faces of a Platonic solid are regular polygons of the same size, and all the vertices look identical. We also demands that our Platonic solids be convex. There are only five Platonic solids:
The story goes on... but in higher dimensions one usually uses the term 'regular polytopes' instead of 'Platonic solids'. All the faces of a regular polytope must be lower-dimensional regular polytopes of the same size and shape, and all the vertices, edges, etc. have to look identical. Maximal symmetry, that's the name of the game! (Also, I'll only be talking about convex polytopes.)
In 4 dimensions, there are exactly six regular polytopes:
You might things would keep getting more complicated in higher dimensions. But it doesn't! 4-dimensional space is the peak of complexity as far as regular polytopes go. From then on, it gets pretty boring. This is one of many examples of how 4-dimensional geometry and topology are more complicated, in certain ways, than geometry and topology in higher dimensions. And the spacetime we live in just happens to be 4-dimensional. Hmm.
In 5 or more dimensions, there are only three regular polytopes:
How can we understand the proliferation of regular polytopes in 4 dimensions? And how can we visualize them?
For starters, try Tony Smith's webpage. If you cross your eyes while gazing at this stereoscopic pair of images, you will see a 24-cell rotating in the 4th dimension, with the 4th dimension depicted using color. If you gaze long enough, you may become enlightened.
Here's a fun way to start visualizing the 4-dimensional regular polytopes.
Ever make a cube out of paper? You draw six squares on the paper in a cross-shaped pattern, cut the whole thing out, and then fold it up.... To do this, we take advantage of the fact that the interior angles of 3 squares don't quite add up to 360 degrees: they only add up to 270 degrees. So if we try to tile the plane with squares in such a way that only 3 meet at each vertex, the pattern naturally "curls up" into the 3rd dimension - and becomes a cube!
The same idea applies to all the other Platonic solids. And we can understand the 4d regular polytopes in the same way!
For example: suppose you take a cube and push in the middle of each face, making a dent shaped like an inverted pyramid. Keep pushing in until the tips of all these pyramids meet at the cube's center.
Now you have a cube with 6 pyramid-shaped dents that meet at a point in the center. Isn't it tempting to take 6 regular octahedra and fit their corners into these dents? If they fit perfectly, maybe we could tile 3-dimensional space with regular octahedra, 6 meeting at each vertex!
Alas, they don't fit perfectly: there's a little "wiggle room". You can either take my word for this, or check it yourself....
But we can snatch victory from the jaws of defeat. We can't tile 3d space with octahedra this way, but if we let the pattern "curl up" into the 4th dimension, we get a 4d regular polytope! This is the 24-cell. It has 24 octahedral faces, 6 meeting at each vertex.
Next let's do the same trick starting with a regular tetrahedron. Push in each triangular face, getting a dent in the shape of somewhat squat triangular pyramid. Keep pushing until the tips of all these dents meet at the center of our original tetrahedron.
Now stick a regular tetrahedron in each dent. There's a lot of wiggle room this time. So let the pattern curl up into the 4th dimension... and get the 4-simplex, with 5 tetrahedral faces, 4 meeting at each vertex!
In fact, there's so much room in these dents that we can even stick the corner of a cube in each one. If we do this, there's still some wiggle room - and if we let the pattern curl up into the 4th dimension, we get the hypercube, with 8 cubical faces, 4 meeting at each vertex!
Actually, we can even go further - we can stick the corner of a dodecahedron in each dent. This time there's only a tiny bit of wiggle room. If we let the pattern curl up, we get the 120-cell, with 120 dodecahedral faces, 4 meeting at each vertex!
This is fun - so let's try another Platonic solid. This time, let's start with a regular octahedron. Push in each of the 8 triangular faces, getting dents in the shape of triangular pyramids. Keep pushing until the dents meet at the middle, and then stick a regular tetrahedron in each of the 8 dents! There's some wiggle room - though not as much as last time - so again, let the pattern curl up in 4-dimensional space... and get the 4-dimensional cross-polytope, with 16 tetrahedral faces, 8 meeting at each vertex!
Next, let's take an icosahedron and do the same trick. Push in each of the 20 triangular faces, making dents in the shape of triangular prisms, and keep pushing until the tips of all these dents meet at the center of the icosahedron. Now stick a regular tetrahedron in each dent. There's only a tiny bit of wiggle room this time! But go ahead, let the pattern curl up into the 4th dimension.... and get the hypericosahedron, with 600 tetrahedral faces, 20 meeting at each vertex!
(Note the pattern: the less wiggle room we have, the bigger our 4d regular polytope is.)
Finally, let's do the same procedure starting from a dodecahedron. Here each dent looks like it wants the corner of an icosahedron put into it - so go ahead and try!
Hmm. Wait a minute! Is there wiggle room this time, or not? And even if there is, are we guaranteed to get a regular polytope using this trick?
I'll leave this as a little puzzle for you... If you give up, click here.
While you're pondering that, let me tell you another way to get some of the 4d regular polytopes. This method involves quaternions, which are a souped-up version of the complex numbers with three square roots of -1, called i, j, and k. A typical quaternion looks like this:
where a,b,c, and d are real numbers. To multiply the quaternions, you need to use these rules, invented by Hamilton back in 1843:
Let's start with the 24-cell, since this guy has no analog in other dimensions. Since the vertices of the 24-cell lie on the unit sphere in 4 dimensions, we can think of its vertices as certain unit quaternions. The 24-cell happens to have, not only 24 faces, but also 24 vertices! We can take them to be precisely the unit "Hurwitz integral quaternions", which are quaternions of the form
where a,b,c,d are either all integers or all integers plus 1/2. One can check that the Hurwitz integral quaternions are closed under multiplication, so the vertices of the 24-cell form a subgroup of the unit quaternions. A regular polytope that's a symmetry group in its own right - ponder that while you cross your eyes and gaze at it spinning around!
Similarly, the 600-cell has 120 vertices, which we can think of as certain unit quaternions. We can take them to be precisely the unit "icosians". These are quaternions of the form
where a,b,c,d all live in the "golden field" - meaning that they're of the form x + √5 y where x and y are rational. Since the icosians are closed under multiplication a group under multiplication, the vertices of the 120-cell also form a group!
The vertices of the 4-dimensional cross-polytope also form a subgroup of the unit quaternions. But this one is a little less exciting. We just take the quaternions of the form
where one of the numbers a,b,c,d is 1 or -1, and the rest are zero. This 8-element subgroup is sometimes called "the quaternion group".
Those are all the 4-dimensional regular polytopes that are also groups. Three out of six ain't bad! But we can get most of the rest using duality.
In general, the 'dual' of a regular polytope is another polytope, also regular, having one vertex in the center of each face of the polytope we started with. The dual of the dual of a regular polytope is the one we started with (only smaller). So polytopes come in mated pairs - except for some 'self-dual' ones.
In 2 dimensions, every regular polytope is its own dual.
In 3 dimensions, the tetrahedron is self-dual. The dual of the cube is the octahedron. And the dual of the dodecahedron is the icosahedron.
In 4 dimensions, the 4-simplex is self-dual. The 24-cell is also self-dual - that's why it had 24 faces and also 24 vertices! The dual of the hypercube is the 4-dimensional cross-polytope. The dual of the 120-cell is the 600-cell.
In higher dimensions, the n-simplex is self-dual, and the dual of the n-cube is the n-dimensional cross-polytope.
But what is so special about 4 dimensions, exactly?
Well, there are very few dimensions in which the unit sphere is also a group. It happens only in dimensions 1, 2, and 4! In 1 dimensions the unit sphere is just two points, which we can think of as the unit real numbers, -1 and 1. In 2 dimensions we can think of the unit sphere as the unit complex numbers, exp(i theta). In 4 dimensions we can think of the unit sphere as the unit quaternions.
Only in these dimensions do we get polytopes that are also groups in a natural way. In 2 dimensions all the regular n-gons correspond to groups consisting of the unit complex numbers exp(2πi / n). In 4 dimensions things are more subtle and interesting. It's especially interesting because the group of unit quaternions, also known as SU(2), happens to be the 'double cover' of the rotation group in 3 dimensions. Roughly speaking, this means that there is a nice function sending 2 elements of SU(2) to each rotation in 3 dimensions.
This gives a slick way to construct the 600-cell, or hypericosahedron. Take the icosahedron in 3 dimensions. Consider its group of rotational symmetries. This is a 60-element subgroup of the rotation group in 3 dimensions. Now look at the corresponding subgroup of SU(2) - its 'double cover', so to speak. This is a 120-element subgroup of the unit quaternions. These are the vertices of the hypericosahedron! So in a very real sense, the hypericosahedron is just the symmetries of the icosahedron! This trick doesn't work in higher dimensions. This is one thing that's very cool about 4 dimensions - it inherits the hypericosahedron and the hyperdodecahedron from the the fact that the icosahedron and dodecahedron happen to exist in 3 dimensions.
Similarly, the 24-cell comes from the symmetries of the tetrahedron!
The rotating Platonic solids above have been copied from Wikipedia article on Platonic solids under the terms of the GNU Free Documentation License. This article is a great place to get started on understanding the Platonic solids.
I have also used links to Eric Weisstein's webpages of 4d regular polytopes, at his World of Mathematics website. He also has lots of information on Platonic solids and other polyhedra. You can rotate the Platonic solids using your mouse!
Andrew Weimholt has a nice website featuring 'foldout models' of 4d regular polytopes. The idea here is that if you could access the fourth dimension, you could fold these up to form 4d regular polytopes. Even if you're trapped in 3 dimensions, they give some extra intuition for what the 4d regular polytopes look like.
If you have access to VRML, you can also have fun with George Hart's Encyclopedia of Polyhedra, which has over 1000 polyhedra in it. (VRML stands for "virtual reality modelling language", and it's available as a plugin for most browsers.)
If you want to learn a lot about regular polytopes, read this book by the king of geometry:
For more about the icosahedron, see "Some thoughts on the number six."
For more about icosians and related marvels, see week20 of This Week's Finds.
For more about the Platonic solids, how fool's gold fooled the Greeks into inventing the regular dodecahedron, and highly symmetric structures in higher dimensions, see week62, week63, week64, and week65 of my weekly column on mathematical physics. This story continues at a deeper level in week186 and week187.
For more on the Hurwitz integral quaternions and the mysteries of triality in 8 dimensions, see week91.
For a deeper look at relations between different Platonic solids, and also more stuff about the 24-cell and 600-cell, see week155.
Everything sufficiently beautiful is connected to all other beautiful things! Follow the beauty and you will learn all the coolest stuff. The Platonic solids are a nice place to start.

© 2006 John Baez
baez@math.removethis.ucr.andthis.edu