six

Some Thoughts on the Number 6

John Baez

September 2, 2015

There are symmetries of the symmetry group of a 6-element set that don't come from symmetries of that set. This is only true for the number 6. It is a truly amazing property of the number 6, which turns out to be connected to many things.

In math jargon, we say that the symmetric group $S_6$ has outer automorphisms. This article explains three ways to think about $S_6$ and its outer automorphisms:

The icosahedron and the number six.
The Tutte–Coxeter graph.
The hypercube of duads.

The icosahedron and the number six

First, buy, borrow or steal, or at least draw, a regular icosahedron! If you can't do any of those, take a look at Greg Egan's webpage, which is a nice companion to this one.

The regular icosahedron is a beautiful thing. It has 20 faces, each an equilateral triangle. Since it is dual to the dodecahedron, it has 12 vertices. If you don't believe me, count them! And by Euler's formula: \[ F — E + V = 2 \] it has 30 edges. (Again, I encourage you to count them. In what follows you will need to grok this fact, not just believe it.)

Puzzle 1. Prove that the regular icosahedron exists.

What? Yes, prove there is a solid with 20 faces all congruent equilateral triangles, five meeting at each vertex! For all you know, it might not exist — the faces might not be able to be precisely equilateral! We wouldn't want to be studying a nonexistent object.

Okay, now think of the regular icosahedron as being centered at the origin. Then each vertex $x$ has an antipodal vertex $-x$. Draw the line segment from $x$ to $-x$; let's call it an axis. There are 6 axes. If we draw the "top" of the icosahedron, the vertices look like this:

                           *

                      *         *
                           *
                        
                        *     *

and each axis contains one of these 6 vertices as one of its endpoints. We will use this picture to keep track of the axes.

Okay, now let's call a pair of axes a duad. Please consult your icosahedron and contemplate a duad. A duad forms the diagonals of a rectangle whose four corners are vertices of the icosahedron.

Puzzle 2. Show that this is a golden rectangle, that is, the long side is $(1 + \sqrt{5})/2$ as long as the short side.

Now since a duad is determined by a choice of two axes, there are \[ {6 \choose 2} = 15 \] duads. We can easily use duads to count how many symmetries the icosahedron has — rotations, that is, but not reflections. Any symmetry of the icosahedron maps a duad to another duad. We can map a fixed duad to any other duad in four different ways (since a rectangle, hence a duad, has 4- fold symmetry.) If you think about it, knowing where a fixed duad goes completely determines the rotation of the icosahedron. Thus there are $4 ×l 15 = 60$ rotational symmetries.

Let us call a set of 3 duads, no two having an axis in common, a syntheme. Since there are 6 axes, 2 per duad, a syntheme completely accounts for all the axes. We can call the 3 duads in a syntheme A, B, and C, and draw the syntheme thus:

                           A

                      B         B
                           A
                        
                        C     C

(for example). Here we are just showing which of the top 6 vertices lie in which duad.

It is infinitely more beautiful, however, to stare at your icosahedron and visualize the 3 interlocking duads in the above syntheme. Each duad determines a golden rectangle, and in the above syntheme these golden rectangles are all perpendicular!

Someone named lyongraulty has even made a little movie of this idea:

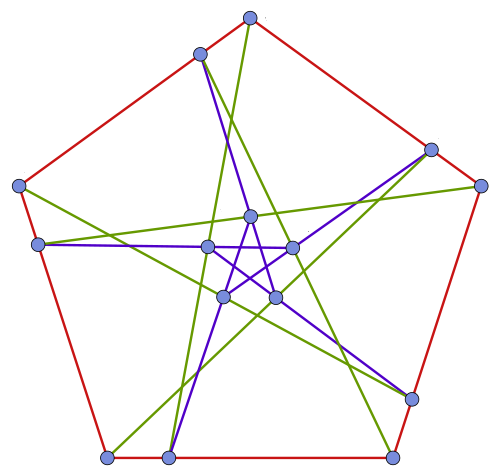
Let us call this kind of syntheme a true cross. There are 5 true crosses, namely the above one and 4 more obtained by rotating it, for example this:

                           B

                      C         A
                           A
                        
                        C     B

and so on. Note that Puzzle 2 and the contemplation of the true cross easily allow one to solve:

Puzzle 3. Let $\Phi = (1 + \sqrt{5})/2$. Show that the 12 points \[ (±\Phi, ±1, 0), \] \[ (±1, 0, ±\Phi), \] \[ (0, ±\Phi, ±1) \] are the vertices of a regular icosahedron.

Of course Puzzle 3 gives a way to solve Puzzle 1, but there is an infinitely more simple and charming solution of Puzzle 1.

If you understand how the icosahedron is dual to the dodecahedron, you can easily use Puzzle 3 to do:

Puzzle 4. Show that the 20 points \[ (±1/\Phi, ±\Phi, 0), \] \[ (±\Phi, 0, ±1/\Phi), \] \[ (0, ±1/\Phi, ±\Phi), \] \[ (±1, ±1, ±1) \]

are the vertices of a regular dodecahedron.

Now, let's use the fact that there are 5 true crosses to determine the symmetry group of the icosahedron. Any symmetry of the icosahedron (again, not including reflections) determines a permutation of the true crosses, and knowing the permutation allows us to reconstruct the symmetry. It follows that the symmetry group of the icosahedron is a subgroup of the group of permutations of 5 objects, $S_5$.

Which permutations can we get? Well, by rotating the pentagon as we were doing above, we clearly get all cyclic permutations. In fact, one can check:

Puzzle 5. The symmetries of the icosahedron correspond to the even permutations of the 5 true crosses.

Thus the symmetry group of the icosahedron is the group of even permutations of 5 objects, the alternating group A₅. This of course has $5!/2 = 60$ elements.

Note that the group $A_5$ acts as symmetries of the set of 6 axes. This action is transitive, that is, any axis can be mapped to any other. Thus we have an interesting way of thinking of $A_5$ as a subgroup of $S_6$. This is more interesting than the boring way where we let $A_5$ act as even permutations of 5 of the 6 things while holding the sixth one fixed.

Puzzle 6. Does this interesting inclusion of $A_5$ in $S_6$ extend to an inclusion of $S_5$ in $S_6$? (See the end of the article for the solution.)

Now, back to synthemes! We have been talking about 5 of them, the true crosses. But there are 5 of a different sort, which look like this:

                           A

                      B         C
                           A
                        
                        C     B

and the rotated versions thereof. By applying other symmetries of the icosahedron to the above one also gets

                           A

                      B         C
                           A
                        
                        B     C

and the rotated versions thereof. There are thus 10 synthemes of this sort in all; we'll call such a syntheme a skew cross.

Robert Dawson made nice pictures of a true cross, on the left, and a skew cross, on the right:

You can see them in motion on Greg Egan's page.

Puzzle 7. Show every syntheme is a true cross or a skew cross.

There are thus 15 synthemes in all. Note that the symmetries of the icosahedron act transitively on the 10 skew crosses, giving us an interesting embedding of $A_5$ in $S_{10}$.

Puzzle 8. Show every duad lies in 3 synthemes — one true cross and two skew crosses.

Thus we have a nice duality: 15 duads and 15 synthemes, 3 duads in each syntheme, and 3 synthemes containing each duad! In Coxeter's essay he draws a picture of this setup.

There are various ways to pick 5 synthemes such that each duad lies in exactly one of the synthemes. Let us call such a choice of 5 synthemes a synthematic total. For example, we may choose the 5 true crosses: each duad lies in exactly one of the true crosses.

(In case you're wondering who made up all these weird terms like 'duad', 'syntheme' and 'synthematic total', it was the famous mathematician James Joseph Sylvester. He came up with most of these ideas around 1844.)

There are 6 synthematic totals. One consists of the 5 true crosses:

     A                B                  C                 C                 B

B         B      C         A        C         B       B         C       A         C
     A                A                  A                 A                 A
                                 
  C     C          C     B            B     A           A     B           B     C

There are five more synthematic totals consisting of one true cross and 4 skew crosses, like this:

      A                B                C                 C                  B

 B         B      C         A      B         C       C         B        A         C
      A                A                A                 A                  A

   C     C          B     C          B     A           A     B            C     B

and the 4 similar pictures you get by rotating this one.

Puzzle 9. There are only 6 synthematic totals!

Now any permutation of the 6 axes induces a permutation of the 6 synthematic totals. This defines a homomomorphism from $S_6$ to itself. And this is the mysterious and sublime outer automorphism of $S_6$. Chris Heinrich gave pleasantly terse explanation of why it's an outer automorphism:

Consider 6 things, e.g. the numerals $1,2,3,4,5,6$. There are 15 non-ordered pairs of them. (Call these duads.) Also there are 15 ways to divide the original set into three duads, e.g. $\{1,2\},\{3,4\},\{5,6\}$. Call these synthemes. Five synthemes can be chosen so as to contain each duad exactly once; and there turn out to be exactly six ways to make this choice. You can label these six sets $A,B,C,D,E,F$. Then a permutation of $1,2,3,4,5,6$. induces a permutation of $A,B,C,D,E,F$. A two-cycle such as (12) induces a product of three disjoint two-cycles such as $(AB)(CD)(EF)$, so the map from one permutation to the other cannot be an inner automorphism.

Puzzle 10. Take the embedding of $A_5$ in $S_6$ described above and compose it with the outer automorphism of $S_6$. What does the image look like as a subgroup of $S_6$? I haven't worked it out, but I bet it's the group consisting of even permutations of $1,2,3,4,5,6$ which leave the element $1$ alone. Here $1,2,3,4,5,6$ are the six synthematic totals and $1$ is the synthematic total consisting of the true crosses.

The Tutte-Coxeter graph

Now let's look at $S_6$ from a different viewpoint! I'll repeat some things I said before, to make this section self-contained. But it uses more advanced math than the last one.

This picture shows the Tutte–Coxeter graph. This graph was discovered by the famous graph theorist William Thomas Tutte in 1947, but its remarkable properties were studied further by him and the geometer H. S. M. Coxeter in a pair of papers published in 1958.

One way to construct this graph starts with the Cremona–Richmond configuration. This is a configuration of 15 points and 15 lines, with 3 points on each line and 3 lines through each point, and containing no triangles:

The red vertices in the Tutte–Coxeter graph correspond to the 15 points of the Cremona–Richmond configuration, while the blue vertices correspond to the 15 lines. An edge connects a red vertex to a blue vertex iff the corresponding point lies on the corresponding line. So, we say the Tutte–Coxeter graph graph is the Levi graph of the Cremona–Richmond configuration.

Since there are 15 points and 15 lines in the Cremona–Richmond configuration, the Tutte–Coxeter graph has 30 vertices. Since each point in the Cremona–Richmond configuration lies on 3 lines, the Tutte–Coxeter graph has 45 edges.

The Cremona–Richmond configuration, in turn, is best understood in terms of special features of $S_6$, the only symmetric group to possess an outer automorphism.

Let $S = \{1,2,3,4,5,6\}$. Of course the symmetric group $S_6$ acts on $S$, but James Sylvester found a different action of $S_6$ on a 6-element set, which in turn gives an outer automorphism of $S_6$.

To do this, he made the following definitions:

A duad is a 2-element subset of $S$. Note that there are $ {6 \choose 2} = 15 $ duads.

A syntheme is a set of 3 duads forming a partition of $S$. There are also 15 synthemes.

A synthematic total is a set of 5 synthemes partitioning the set of 15 duads. There are 6 synthematic totals.

Any permutation of $S$ gives a permutation of the set $T$ of synthematic totals, so we obtain an action of $S_6$ on $T$. Choosing any bijection betweeen $S$ and $T$, this in turn gives an action of $S_6$ on $S$, and thus a homomorphism from $S_6$ to itself. Sylvester showed that this is an outer automorphism.

We can interpret all this combinatorics in terms of the Cremona–Richmond configuration. The points of the Cremona–Richmond configuration are the 15 duads. Similarly, the lines of this configuration are the 15 synthemes. We say that a point lies on a line iff the corresponding duad lies in the corresponding syntheme.

Since the square of the outer automorphism of $S_6$ is the identity, switching points and lines in the Cremona–Richardson configuration gives another Cremona–Richardson configuration.

We can also interpret this combinatorics directly in terms of the Tutte–Coxeter graph. Greg Egan has drawn a version of the Tutte–Coxeter graph with duads and synthemes:

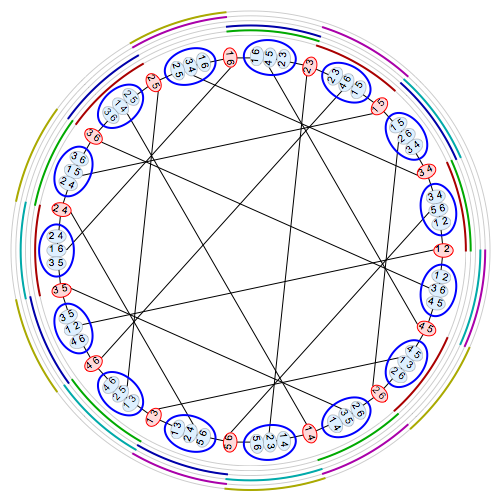
Here the 15 red vertices of the Tutte–Coxeter graph are drawn as duads, while the 15 blue vertices are drawn as synthemes. We draw an edge from a duad to a syntheme whenever the duad lies in the syntheme. You can see that there are 3 duads in each sytheme, and each duad lies in 3 synthemes.

The 6 concentric rings around the picture are the 6 synthematic totals. A band of color appears in one of these rings near some syntheme if that syntheme is part of that synthematic total.

The outer automorphisms of $S_6$ give symmetries of the Tutte–Coxeter graph that switch the red and blue vertices. The inner automorphisms, which correspond to elements of $S_6$, also give symmetries: for each element of $S_6$, the Tutte–Coxeter graph has a symmetry that permutes the numbers in the picture.

The group $\mathrm{Aut}(S_6)$ has $$ 2 \times 6! = 1440 $$ elements, coming from the $6!$ inner automorphisms of $S_6$ and a chosen outer automorphism of order 2. In fact, $\mathrm{Aut}(S_6)$ is the whole symmetry group of the Tutte–Coxeter graph.

How do the outer automorphisms of $S_6$ give symmetries of the Tutte–Coxeter graph that switches the red and blue vertices? There are various ways to see this. Greg Egan gave one, which focuses on the reverse question: how do symmetries of the Tutte–Coxeter graph give automorphism of $S_6$?

Let $\mathrm{Symm}(TC)$ be the complete symmetry group of the Tutte–Coxeter graph. We'll construct a homomorphism $$ \psi \colon \mathrm{Symm}(TC) \to \mathrm{Aut}(S_6) $$ and sketch out why it's an isomorphism.
We know there's an isomorphism between $S_6$ and the subgroup of the symmetries of the Tutte-Coxeter graph that preserve the duad/syntheme distinction. We'll call this $$ \phi \colon S_6 \to \mathrm{Symm}_0(TC), $$ where $\mathrm{Symm}_0(TC)$ is the subgroup where duads and synthemes don't mix.
Suppose $g$ is any element of $\mathrm{Symm}(TC)$, and we want to obtain an automorphism of $S_6$, $ \psi (g) \colon S_6 \to S_6 $. For any permutation $p \in S_6$, we define: $$ \psi(g)(p) = \phi^{-1}(g \phi(p) g^{-1}) $$ So we act with the inverse of our graph symmetry $g$, then act with the graph symmetry corresponding to the permutation $p$, then act with the graph symmetry $g$... and then turn the resulting overall graph symmetry into an element of $S_6$.
This is well-defined for any $g$ in $\mathrm{Symm}(TC)$, even if $g$ swaps duads and synthemes, because we use both $g$ and $g^{-1}$, and $\phi(p)$ preserves the duad/syntheme distinction, so the product: $$ g \phi(p) g^{-1} $$ will be in $\mathrm{Symm}_0(TC)$.
It is easy to check that any inner automorphism of $S_6$ is in the range of $\psi$. I checked that outer automorphisms are in the range too, by explicitly turning a reflection symmetry of the graph that swaps duads and synthemes into an automorphism of $S_6$. It wasn't an inner automorphism. Thus, $\psi$ is onto. To check that it's one-to-one, the main step is to note that it's one-to-one on $\mathrm{Symm}_0(TC)$, because this group, isomorphic to $S_6$, has trivial center.

Another method, more complicated but appealing in some ways, follows ideas borrowed from Klein's Erlangen Program. The idea here is to build geometries starting from groups. If a group $G$ acts on some geometrical structure, any 'figure' in this structure will be stabilized by some subgroup of $G$. We can turn this around by defining 'figures' to be subgroups of $H$.

We can use this idea to define the Tutte–Coxeter graph in a way that makes it obviously have $\mathrm{Aut}(S_6)$ as symmetries. Let $G$ be a group abstractly isomorphic to $S_6$, but let's not think of it as a group of permutations of a 6-element set, since the whole point is that we can do this in two inequivalent ways, related by an outer automorphism, and we don't want to break the automorphism symmetry by favoring either way.

One can look up in a table that $G$ has 30 subgroups isomorphic to $S_4 \times S_2$. These will be the vertices of our graph.

Given two such subgroups, $H$ and $H'$, we draw an edge between the corresponding vertices iff $H \cap H'$ is isomorphic to $D_4 \times S_2$, where $D_4$ is the 8-element dihedral group that acts as symmetries of a square.

Since we built it from $G$, the resulting graph is obviously acted on by $\mathrm{Aut}(G) \cong \mathrm{Aut}(S_6)$. What is not obvious is that it is the Tutte–Coxeter graph! For this we need some more facts about subgroups of $S_6$.

The 30 subgroups of $G$ isomorphic to $S_4 \times S_2$ come in two classes: 15 are conjugate to each other, and the other 15 are conjugate to each other. If we identify $G$ with a group of permutations of a 6-element set, 15 of these subgroups are stabilizers of duads, while the other 15 are stabilizers of synthemes.

However, which is which? That depends on how you identify $G$ with a group of permutations of a 6-element set! Here we are deliberately not making that decision.

But suppose we do. If $H$ is the stabilizer of a duad, and $H'$ is the stabilizer of a syntheme, and the duad lies in the syntheme, then $H \cap H'$ will be isomorphic to $D_4 \times S_2$. In other cases, $H \cap H'$ will not be isomorphic to $D_4 \times S_2$. So, our construction gives the Tutte–Coxeter graph.

In fact, $G$ has exactly 45 subgroups isomorphic to $D_4 \times S_2$ so we can identify the edges of our graph with these subgroups.

For the necessary facts about subgroups of $S_6$, see:

Götz Pfeiffer, Subgroups.

By the way, the Tutte–Coxeter graph is a (3,8)-cage! What does that mean? Well, for starters, the Tutte–Coxeter graph is a (3,8)-graph, meaning that every vertex has 3 neighbors and every cycle has length at least 8. Second, it has the fewest possible vertices for a (3,8)-graph, so it is called a (3,8)-cage. It is, in fact, the unique (3,8)-cage.

Here are some more puzzles. Answers are at the end of this article:

Puzzle 11. How many cycles of length 8 does the Tutte–Coxeter graph contain?

Puzzle 12. What do these cycles correspond to in the Cremona–Richmond configuration?

Puzzle 13. What do these cycles correspond to in terms of duads, synthemes or other features of the 6-element set?

The Hypercube of Duads

And now here's yet another take on the group $S_6$. Again I'll repeat myself a bit, to make this somewhat self-contained. But this will use even more advanced math!

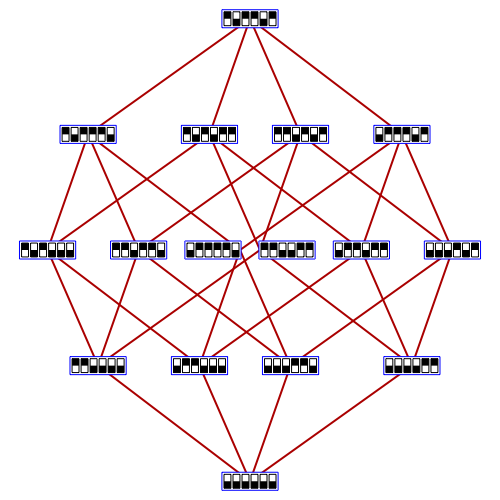
This picture by Greg Egan shows a hypercube with all vertices except the bottom labelled by duads, that is, 2-element subsets of a 6-element set. There are 15 duads, while the hypercube has 16 vertices.

In fact, we can think of this hypercube as a 4-dimensional vector space over the field with two elements, $\mathbb{F}_2$. Even better, doing this gives a nice proof that $S_6$, the symmetric group consisting of permutations of 6 letters, is isomorphic to $ \mathrm{Sp}(4,\mathbb{F}_2) $, the group of symplectic transformations of a 4-dimensional symplectic vector space over $\mathbb{F}_2 $.

To see this, start with the 6-dimensional vector space $\mathbb{F}_2^6$. Then form the 5-dimensional subspace consisting of vectors whose coordinates sum to zero: $$ U = \{ v \in \mathbb{F}_2^6 : \; v_1 + \cdots + v_6 = 0 \} $$ Note that the vector $$ u = (1,1,1,1,1,1) $$ lies in $U$. Thus, we can form a 4-dimensional quotient space $$ V = U/\langle u \rangle $$ In fact, all 15 nonzero vectors in $V$ correspond to duads! To see this, note that there are four kinds of vectors in $U$:

$ (0,0,0,0,0,0) $,
$ (1,1,0,0,0,0) $ and the vectors obtained from this by permuting coordinates,
$ (1,1,1,1,0,0) $ and the vectors obtained from this by permuting coordinates,
$ (1,1,1,1,1,1 )$.

Adding $u$ to the vector of the first kind produces the vector of the last kind, and vice versa. Adding $u$ to a vector of the second kind gives one of the third kind, and versa. So, in $V = U/\langle u \rangle $, every vector is equivalent to one of the first or second kinds. But vectors of the second kind correspond naturally to duads. Thus, every nonzero vector in $V$ corresponds naturally to a duad.

In the picture, Egan has somewhat arbitrary chosen a basis for $V$ consisting of the equivalence classes of the vectors $$ (1,1,0,0,0,0), \quad (0,1,1,0,0,0), \quad (0,0,0,1,1,0), \quad (0,0,0,0,1,1) $$ These form the second to bottom row in the hypercube, next to the origin. The other vectors are all linear combinations of these.

Even better, the original vector space $\mathbb{F}_2^6$ has a symplectic structure on it, meaning a nondegenerate alternating bilinear form. This bilinear form $$ \omega : \mathbb{F}_2^6 \times \mathbb{F}_2^6 \to \mathbb{F}_2 $$ is given by $$ \omega((a,b,c,d,e,f), (a',b',c',d',e',f')) = (ab' - ba') + (cd' - dc') + (ef' - fe') . $$ The minus signs are only to reassure readers familiar with symplectic structures in other contexts; over $\mathbb{F}_2$ they have no effect. So, for any vector $v = (a,b,c,d,e,f)$ we have $$ \omega(u,v) = a + b + c + d + e + f $$ Thus, $U$ consists of the vectors $v$ with that are orthogonal to $u$ in the sense that $\omega(u,v) = 0$. In particular, $u \in U$ is orthogonal to itself. Using these facts, one can check that the quotient space $V = U/\langle u \rangle$ inherits a symplectic structure from $\mathbb{F}_2^6$: if $[v],[w] \in V$ are equivalence classes, $\omega(v,w)$ is independent of the choice of representatives $v,w \in U$, and this defines a symplectic structure on $V$. This process of taking a symplectic structure and getting one on a quotient space of a subspace is an example of 'symplectic reduction'.

The group of linear transformations preserving the symplectic structure on a 4-dimensional symplectic vector space over the field $\mathbb{F}_2$ is called the symplectic group $\mathrm{Sp}(4,\mathbb{F}_2)$, or $\mathrm{Sp}(4,2)$ for short. This acts on $V$, and thus acts as permutations of the 15 duads.

The group $S_6$ acts by permutation of coordinates on $V$, so it too acts to permute the 15 duads. This suggests that perhaps $$ S_6 \cong \mathrm{Sp}(4,\mathbb{F}_2) $$ and indeed this is true. There are various ways to see this.

One method is to note that the action of $S_6$ by permuting coordinates on $V$ preserves the symplectic structure on $V$. This gives a homomorphism $$ S_6 \to \mathrm{Sp}(4,\mathbb{F}_2) $$ This homomorphism is 1-1 because every nontrivial permutation in $S_6$ acts nontrivially on duads, which correspond to nonzero elements of $V$. To check that it is onto, it suffices to show both groups have the same number of elements. The group $S_6$ has $6! = 720$ elements, while for symplectic groups we have this general formula: $$ \vert \mathrm{Sp}(2m,\mathbb{F}_q)\vert = \prod_{i = 1}^m (q^{2i} - 1)q^{2i-1} $$ which gives $$ \vert\mathrm{Sp}(4,\mathbb{F}_2)\vert = (2^2 - 1)2^1 \cdot (2^4 - 1)2^3 = 3 \cdot 2 \cdot 15 \cdot 8 = 720 . $$ A more conceptual approach, which inspired the more plodding one above, was offered by Tim Silverman on the n-Category Café. Silverman focuses on the projective symplectic group $\mathrm{PSp}(4,\mathbb{F}_2)$, formed by taking the symplectic group and modding out by invertible scalars. However, since 1 is the only invertible element of $\mathbb{F}_2$, this is the same as $\mathrm{Sp}(4,\mathbb{F}_2)$. He writes:

Here is how $S_6$ is isomorphic to $\mathrm{\mathrm{PSp}}(4, \mathbb{F}_2)$.
Take a $6$-dimensional vector space over $\mathbb{F}_2$: say sextuples of ones and zeros. Take the subspace orthogonal to $\left(1,1,1,1,1,1\right)$, getting a 5-dimensional space, consisting of sextuples with an even number of ones. Then take the quotient by addition of $\left(1,1,1,1,1,1\right)$, getting a $4$-dimensional space.
Now think of this in another way: the first space is the set of subsets of a set $S$ of $6$ elements corresponding to coordinates (for each each vector, take the subset of coordinates consisting of those with a component value of $1$). The $5$-dimensional subspace consists of subsets of even cardinality. The quotient identifies subsets with their complements. Sum of vectors is symmetric difference of sets.
There are two types of element in the $4$-dimensional space: the identity, consisting of the equivalence class $$ \left\{\left(0,0,0,0,0,0\right), \left(1,1,1,1,1,1\right)\right\}, $$ or, in the alternative formulation the empty set together the whole of $S$; and the other elements, all of which are two-element equivalence classes containing a $2$-element subset of $S$ together with its $4$-element complement.
If we go over to projective space, all we do is throw away the origin (because $\mathbb{F}_2$ only has one non-zero scalar, making everything very simple). This gives us a space whose points are duads.
The vector sum of two duads depends on their overlap. Letting $a, b, c, d, e$ and $f$ be the elements of $S$ in some order:
• $(ab)+(ab) =0$, e.g. $$ \left(1,1,0,0,0,0\right)+\left(1,1,0,0,0,0\right)=\left(0,0,0,0,0,0\right). $$
• $(ab)+(bc)=(ac)$, e.g. $$\left(1,1,0,0,0,0\right)+\left(0,1,1,0,0,0\right)=\left(1,0,1,0,0,0,0\right) .$$
• $(ab)+(cd)=(ef)$, e.g. $$\left(1,1,0,0,0,0\right)+\left(0,0,1,1,0,0\right)=\left(1,1,1,1,0,0\right) \sim \left(0,0,0,0,1,1\right). $$
Then, in the projective space there are two kinds of line, of the form $\left\{(ab),(bc),(ac)\right\}$ and $\left\{(ab),(cd),(ef)\right\}$ respectively.
Now there is a symplectic structure on the duads given by parity of overlap: $$ \omega((ab),(ab))=0 $$ $$ \omega(ab),(bc)) =1 $$ $$ \omega((ab),(cd)) =0 $$ An example symplectic basis would be $\left\{(ab),(bc),(de),(ef)\right\}$.
Since both the vector space (or projective space) structure and the symplectic structure depend only on the overlap between pairs, it's not hard to see that the symplectic group must be $S_6$. The two types of lines are the non-isotropic and isotropic lines respectively. (That is, lines of the form $\left\{(ab),(bc),(ac)\right\}$ have all their points mutually non-orthogonal, and lines of the form $\left\{(ab),(cd),(ef)\right\}$ have all their points mutually orthogonal.)
Thus (necessarily isotropic) points are duads, and isotropic lines are synthemes, explaining why the duads and synthemes with the obvious incidence relation form a generalised quadrangle.
It's a bit tedious to work out, but planes consist of a distinguished duad, together with the $6$ duads formed from the $4$ elements of $S$ not lying in the distinguished duad. The distinguished duad is then the pole of the plane (i.e. the unique point orthogonal to everything in the plane).
These planes are, of course, Fano planes.

References and Acknowledgements

The first part of this article was inspired by discussions on the newsgroup sci.math, and this essay:

H. S. M. Coxeter, Twelve points in $\mathrm{PG}(5,3)$ with 95040 self-transformations, Royal Society Proceedings A 247 (1958), 279–293. Reprinted in H. S. M. Coxeter,Twelve Geometric Essays, Dover Books, 1999.

An earlier version of the first part is available in Postscript. For more on the icosahedron, and the truncated icosahedron, check out "week79" of This Week's Finds. Here are some more articles on the outer automorphism of $S_6$:

John Baez, A wrinkle in the mathematical universe, The n-Category Café.

Peter Cameron, The symmetric group, 3, Peter Cameron's Blog.

Noah Snyder, The outer automorphism of $S_6$, Secret Blogging Seminar.

Snyder notes that there are 6 nonisomorphic ways to make a 6- element set into a projective line over the field with 5 elements. This gives the outer automorphism of $S_6$ and also fits in nicely with the fact that $ S_5 \cong \mathrm{PGL}(2, \mathrm{F}_5)$, while $A_5 \cong \mathrm{PSL}(2,\mathbb{F}_5) $ is the symmetry group of the dodecahedron. As we've seen above, the symmetry group of the dodecahedron acts transitively on the 6 axes of the dodecahedron; this corresponds to the transitive action of $\mathrm{PSL}(2,\mathbb{F}_5)$ on the projective line over $\mathrm{F}_5$, which has 6 elements.

Thanks go to Derek Clegg for asking on sci.math, way back in 1992, whether all automorphisms of $S_n$ were inner. This started the whole business. Thanks go to Allen Knutson for saying the answer was yes unless $n = 6$, and to Dave Sibley for some important clues on the relation to icosahedra. Thanks go to Christopher J. Henrich for summarizing the relevant ideas from Coxeter's essay. Coxeter mentions that he could have titled his essay "Some thoughts on the number 6," so I decided to steal that title for this article. Thanks go to Bradley W. Brock for clarifying the nature of the skew crosses, finding the synthematic totals consisting of skew crosses, and creating Puzzle 4. Thanks go to Charles Yeomans and Tom R. for some facts that were too sophisticated to find their way into this article. Thanks go to Greg Egan and Robert Dawson for making nice webpages that illustrate some of these ideas. And most of all, thanks go to Sylvester for inventing duads and synthemes!

J. J. Sylvester, Elementary researches in the analysis of combinatorial aggregation, Philosophical Magazine 24 (1844), 285–296. Reprinted in The Collected Mathematical Papers of James Joseph Sylvester, ed. H. F. Baker, Cambridge U. Press, Cambridge, 1904, pp. 91–102.

Here's a solution to one of the puzzles:

Puzzle 6. Does the nonobvious inclusion of $A_5$ in $S_6$ extend to an inclusion of $S_5$ in $S_6$?

Answer. Yes. Switching the first two true crosses, an odd permutation:

	     A                 B       

	B         B       C         A   
	     A                 A        
                                 
 	  C     C           C     B

is generated by switching axes 1 and 5, 2 and 3, 4 and 6, numbering the axes as follows:

                        1

                   5         2
                        6
                        
                     4     3

Doing this doesn't affect the other three true crosses. The rest of the odd permutations can be reached from this permutation with the known even permutations.

I wrote the second part of this article much later than the first part: it appeared as a post on my blog Visual Insight, along with some extra stuff about the Heawood graph, which I have not included here. For more on the Tutte–Coxeter graph and Cremona–Richardson configuration, see:

Tutte–Coxeter graph, Wikipedia.

Cremona–Richardon configuration, Wikipedia.

The Cremona–Richmond configuration is an example of a generalized quadrangle, and it is sometimes called $\mathrm{GQ}(2,2)$. Richard Green discusses it under that name here:

Richard Green, The generalized quadrangle GQ(2,2).

The third part of this article appeared as another post on Visual Insight, inspired by Tim Silverman's comments on my n-Category Café post.

Here are the answers to Puzzles 11-13, followed by Tim Silverman's explanations:

Puzzle 11. How many cycles of length 8 does the Tutte–Coxeter graph contain?

Answer. 90.

Puzzle 12. What do these cycles correspond to in the Cremona–Richmond configuration?

Answer. They correspond to quadrangles: that is, configurations of 4 distinct points $p_1, \dots, p_4$ and 4 distinct lines $\ell_1, \dots, \ell_4$ where $p_i$ lies on only two of the lines, $\ell_{i \pm 1 \bmod 4} $.