Seminar: Fall 2008

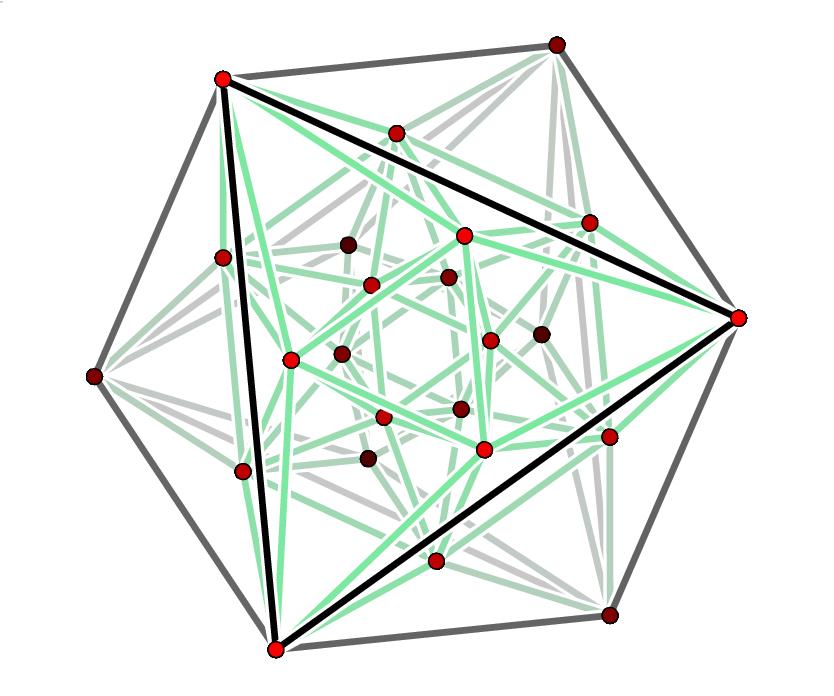
The red dots are the 24 roots of D₄, projected from 4 dimensions down to 3 and then drawn in the plane.
These points are the vertices of the 24-cell, whose edges are also drawn here.

Seminar - Fall 2008

Lie Theory Through Examples

John Baez

Simple Lie groups and Lie algebras tie together some of the most beautiful, symmetrical structures in mathematics: Platonic solids and their higher-dimensional cousins, finite groups generated by reflections, lattice packings of spheres, incidence geometries, symmetric spaces, and more. In this fall's seminar we'll explore this web of ideas through examples, starting with easy 'classical' ones and working up to 'exceptional' ones such as the 248-dimensional Lie group E₈.

Here are the lecture notes, and blog entries where you can ask questions and discuss ideas:

Lecture 1 (Sept. 30) - Introduction. The simplest interesting example: A₂. Blog entry.

We can think of the A₂ lattice as the Eisenstein integers. Here ω is a cube root of 1.
Lecture 2 (Oct. 6) - The Killing form and the A₃ lattice. Blog entry.

Triangular pyramid of balls. The balls' centers form a copy of the A₃ lattice.

A different view makes it clear why the A₃ lattice is also called a "cubic close packing".

You can also think of the A₃ lattice as built from octahedra and tetrahedra. This figure is from Buckminster Fuller's patent for the "octet truss", now widely used in architecture.

In the A₃ lattice, each point has 12 nearest neighbors, which form the vertices of a cuboctahedron.
Lecture 3 (Oct. 21) - Representations of Lie groups. The weight lattice of a simply-connected compact simple Lie group. Blog entry.

Lecture 4 (Oct. 28) - Classifying unitary representations using weights. The example of A₁, which corresponds to the group SU(2). The relation between SU(2) and SO(3), and their representations. The example of A₂, which corresponds to the group SU(3). Blog entry.
Lecture 5 (Nov. 18) - The spin groups.

If you discover any errors in the course notes please email me, and I'll try to correct them. I'll keep a list of errors that haven't been fixed yet.

You can also download LaTeX files of the lecture notes, if for some bizarre reason you want them. However, the authors keep all rights to this work, except when stated otherwise.