The Eightfold Way
John C. Baez

May 27, 2003

Also available in PDF, Postscript and LaTeX

It is natural to group the eight lightest mesons into 4 irreps of isospin $\SU (2)$ as follows:

mesons	I3	Y	Q
pions
(complexified adjoint rep)
$\pi^+$	+1	0	+1
$\pi^0$	0	0	0
$\pi^-$	-1	0	-1
kaons
(defining rep)
$K^+$	+1/2	1	+1
$K^0$	-1/2	1	0
antikaons
(dual of defining rep)
$\overline{K^0}$	+1/2	-1	0
$K^-$	-1/2	-1	-1
eta
(trivial rep)
$\eta$	0	0	0

(The dual of the defining rep of $\SU (2)$ is isomorphic to the defining rep, but it's always nice to think of antiparticles as living in the dual of the rep that the corresponding particles live in, so above I have said that the antikaons live in the dual of the defining rep.)

In his theory called the Eightfold Way, Gell-Mann showed that these eight mesons could be thought of as a basis for the the complexified adjoint rep of $\SU (3)$ -- that is, its rep on the 8-dimensional complex Hilbert space

$$\su (3) \tensor \C \iso \Sl (3,\C) .$$

He took seriously the fact that

$$\Sl (3,\C) \subset \C[3] \iso \C^3 \tensor (\C^3)^*$$

where $\C^3$ is the defining rep of $\SU (3)$ and $(\C^3)^*$ is its dual. Thus, he postulated particles called quarks forming the standard basis of $\C^3$:

$$% latex2html id marker 402 u = \left( \begin{array}{c} 1 \... ...t( \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array}\right) ,$$

and antiquarks forming the dual basis of $(\C^3)^*$:

$$\overline{u} = \left( \begin{array}{ccc} 1 & 0 & 0 \end{ar... ... \left( \begin{array}{ccc} 0 & 0 & 1 \end{array}\right) .$$

This let him think of the eight mesons as being built from quarks and antiquarks. For example, the positive pion corresponds to the matrix

$$% latex2html id marker 404 \pi^+ = \left( \begin{array}{ccc... ... 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right) \in \Sl (3,\C),$$

but as an element of $\C^3 \tensor (\C^3)^*$ this is just

$$% latex2html id marker 405 \left( \begin{array}{c} 1 \\ ... ...cc} 0 & 1 & 0 \end{array}\right) = u \tensor \overline{d}$$

so he said the positive pion is built from an up quark and an down antiquark! After decades of experiment, we now have lots of evidence that quarks really exist and that this is true.

Now a little work for you....

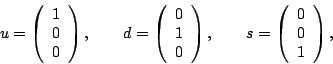
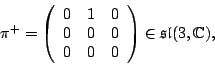
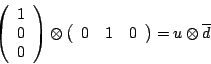
1. Determine in a similar way how the other mesons are built from quarks and antiquarks, and fill in this chart:

$$% latex2html id marker 406 \begin{array}{cll} \par \pi^+ &=... ...1 & 0 \\ 0 & 0 & 2 \\ \end{array} \right) = \\ \end{array}$$

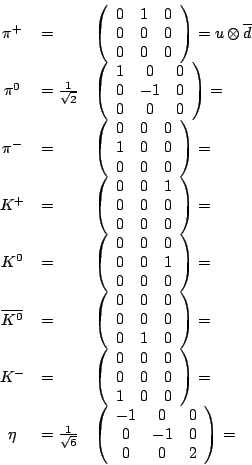
2. In the Eightfold Way, whenever we have particles living in some rep $\rho$ of $\SU (3)$, the third component of weak isospin corresponds to the operator

$$% latex2html id marker 407 I_3 = d\rho \left( \begin{array}... ... & 0 \\ 0 & -1/2 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)$$

while hypercharge corresponds to the operator

$$% latex2html id marker 408 Y = d\rho \left( \begin{array}{c... ... \\ 0 & 1/3 & 0 \\ 0 & 0 & -2/3 \\ \end{array} \right) .$$

As usual, electric charge corresponds to the operator

$$Q = I_3 + \frac{Y}{2} .$$

By calculating how the above operators act on the standard basis of the defining rep, fill out the following table of eigenvalues:

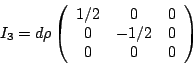
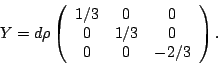
quarks	I3	Y	Q
$u$
$d$
$s$

3. Figure out the same information for the antiquarks:

antiquarks	I3	Y	Q
$\overline{u}$
$\overline{d}$
$\overline{s}$

Hint: Unlike for $\SU (2)$, the defining representation of $\SU (3)$ is not isomorphic to its dual. So, you should go back to the formula for the dual of a Lie algebra rep. If we have a rep of some Lie group

$$\rho \maps G \to \End (V)$$

then the dual rep

$$\rho^* \maps G \to \End (V^*)$$

is defined by

$$(\rho^*(g)f)(v) = f(\rho(g^{-1})v)$$

for all $g \in G$, $f \in V^*$ and $v \in V$. Differentiating all this, we get a Lie algebra rep

$$d\rho \maps \g \to \End (V)$$

whose dual rep

$$d\rho^* \maps \g \to \End (V^*)$$

is given by

$$(d\rho^*(x)f)(v) = -f(d\rho(x)v)$$

for all $x \in \g$, $f \in V^*$ and $v \in V$. Taking $\rho$ to be the defining rep of $\SU (3)$ on $\C^3$, you can use this last formula to work out what $I_3, Y$ and $Q$ do to antiquarks, which form a basis of the dual space $(\C^3)^*$. The final answer should be intuitively obvious, but it's good to see how it comes out of the math!

4. By filling out the following chart, check that you can compute $I_3$, $Y$ or $Q$ for any meson simply by adding these quantities for the quarks and antiquarks it is built from. For example, the $\pi^+$ is built from a $u$ and a $\overline{d}$. The $u$ has $I_3 = \frac{1}{2}$ and the $\overline{d}$ also has $I_3 = \frac{1}{2}$; adding these we get $I_3 = 1$ for the $\pi^+$.

mesons	quark-antiquark descriptions	I3	Y	Q
pions
$\pi^+$	$u \tensor \overline{d}$	$\frac{1}{2} + \frac{1}{2} = +1$	$\qquad\qquad$	$\qquad\qquad$
$\pi^0$
$\pi^-$
kaons
$K^+$
$K^0$
antikaons
$\overline{K^0}$
$K^-$
eta
$\eta$

In terms of the mathematics of representation theory, why should we be able to compute $I_3$, $Y$ or $Q$ for mesons as a sum of this sort?

If we had more time, we would now go on to explain the baryons -- like the proton and neutron, but also other particles -- in terms of quarks. Then we would explain how the Eightfold Way was eventually incorporated into the Standard Model, in which quarks are held together by the `strong force' to form mesons and baryons. Ironically, while the strong force is described by a theory with symmetry group $\SU (3)$, this symmetry group has nothing to do with Gell-Mann's $\SU (3)$ symmetry! Gell-Mann's $\SU (3)$ is now seen to be just an approximate symmetry coming from the fact that the up, down and strange quarks all act roughly the same, though they have different masses and charges. The $\SU (3)$ symmetry of the strong force describes how quarks of any sort come in three `colors'.

But alas, summer is fast approaching, and there is no time to continue our adventure into particle physics. If you want to learn more, try reading these books, in approximately increasing order of difficulty and detail:

• Robert P. Crease and Charles C. Mann, The Second Creation: Makers of the Revolution in Twentieth-Century, Physics, MacMillan, New York, 1986.

• Emilio Segre, From X-Rays to Quarks: Modern Physicists and Their Discoveries, W. H. Freeman, San Francisco, 1980.

• Abraham Pais, Inward Bound: of Matter and Forces in the Physical World, Clarendon Press, New York, 1986.

• T. D. Lee, Particle Physics and Introduction to Field Theory, Harwood, New York, 1981.

• Kerson Huang, Quarks, Leptons & Gauge Fields, World Scientific, Singapore, 1982.

© 2003 John Baez - all rights reserved.
baez@math.removethis.ucr.andthis.edu

home