Also available in PDF,
Postscript and
LaTeX
The symmetry group of the Standard Model is usually said
to be
Although there are many theories,
we don't know why the internal symmetry group of the
Standard Model is what it is. But we do know more than what
I've said so far about what it really is. Whenever we have any
representation ![]() of any group
of any group ![]() :
:
![\begin{displaymath}
% latex2html id marker 357
\begin{diagram}[\End (V)]
\node...
...de{G/N} \arrow{e,t}{\tilde\rho} \node{\End (V)}
\end{diagram}
\end{displaymath}](img23.gif)
The goal of this homework is to determine ![]() where
where
![]() and
and ![]() is
the direct sum of all representations
corresponding to elementary particles in the Standard Model.
Elements of
is
the direct sum of all representations
corresponding to elementary particles in the Standard Model.
Elements of ![]() act as the identity
on all particles, so
act as the identity
on all particles, so ![]() deserves to be
called the true internal symmetry group of the
Standard Model.
deserves to be
called the true internal symmetry group of the
Standard Model.
1. Let ![]() be the algebra of
be the algebra of ![]() complex
matrices. Show that
complex
matrices. Show that ![]() commutes with all
commutes with all
![]() iff
iff ![]() for some complex number
for some complex number
![]() .
.
Hint: given ![]() , assume that
, assume that
![]() for all
for all
![]() , where
, where ![]() is
the elementary matrix with a
is
the elementary matrix with a ![]() in the entry lying
on the
in the entry lying
on the ![]() th row and
th row and ![]() th column, and all other entries equal
to
th column, and all other entries equal
to ![]() . Get enough equations to show
. Get enough equations to show
![]() for some
for some ![]() .
.
2. Let ![]() be the Lie algebra of
be the Lie algebra of ![]() skew-adjoint
complex matrices. Show that
skew-adjoint
complex matrices. Show that ![]() commutes with all
commutes with all ![]() iff
iff ![]() for some complex number
for some complex number ![]() .
.
Hint: Show that any matrix ![]() is of the
form
is of the
form ![]() where
where
![]() . Use this to reduce
Problem 2 to Problem 1.
. Use this to reduce
Problem 2 to Problem 1.
3. Let ![]() be the Lie algebra of
be the Lie algebra of ![]() skew-adjoint
traceless complex matrices. Show that
skew-adjoint
traceless complex matrices. Show that ![]() commutes with all
commutes with all
![]() iff
iff ![]() for some complex number
for some complex number ![]() .
.
Hint: Show that any ![]() is of the form
is of the form
![]() where
where
![]() and
and ![]() . Use this to
reduce Problem 3 to Problem 2.
. Use this to
reduce Problem 3 to Problem 2.
4. Let ![]() be the Lie group of
be the Lie group of ![]() unitary matrices
with determinant 1. Show that
unitary matrices
with determinant 1. Show that ![]() commutes with all
commutes with all ![]() iff
iff ![]() for some complex number
for some complex number ![]() .
.
Hint: We've seen that if
![]() then
then
![]() for all
for all ![]() . Show that if
. Show that if ![]() commutes with
commutes with ![]() for
all
for
all ![]() then
then ![]() commutes with
commutes with ![]() . Use this to reduce
Problem 4 to Problem 3.
. Use this to reduce
Problem 4 to Problem 3.
5. Show that the center of ![]() consists of all
elements of
consists of all
elements of ![]() that are of the form
that are of the form ![]() for
some complex number
for
some complex number ![]() . Show the center is generated
by the matrix
. Show the center is generated
by the matrix
![]() .
.
Hint: Use Problem 4.
Since
![]() is an
is an ![]() th root of unity, it
follows that that the center of
th root of unity, it
follows that that the center of ![]() is isomorphic
to
is isomorphic
to ![]() ! It's easy to see that the center of a product
of groups is the product of their centers. So, the center
of
! It's easy to see that the center of a product
of groups is the product of their centers. So, the center
of
![]() is isomorphic
to
is isomorphic
to
![]() . Or, for short:
. Or, for short:
Now let us work out the subgroup ![]() consisting
of elements that act as the identity on all elementary
particles in the Standard Model.
An element
consisting
of elements that act as the identity on all elementary
particles in the Standard Model.
An element ![]() will be in this subgroup
iff it acts trivially on the fermion rep
will be in this subgroup
iff it acts trivially on the fermion rep ![]() , the gauge
boson rep G,
and the Higgs rep
, the gauge
boson rep G,
and the Higgs rep ![]() .
.
To get started, note that ![]() acts trivially on
G
precisely when
acts trivially on
G
precisely when ![]() is in the center of
is in the center of ![]() . The key to
seeing this is remembering that the gauge boson rep is
the adjoint representation of
. The key to
seeing this is remembering that the gauge boson rep is
the adjoint representation of ![]() !
We can think of
!
We can think of ![]() as a block diagonal
as a block diagonal ![]() matrix
matrix
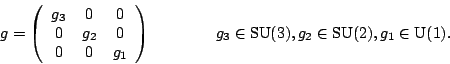
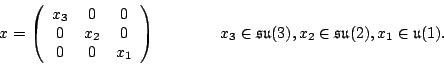
It follows that ![]() must be a subgroup of the center of
must be a subgroup of the center of
![]() :
:
| type of particle | action of | action of | action of |
|
|
|
|
|
|
|
|||
|
|
|||
|
|
6. By Problem 5, the center of ![]() is generated by the
element
is generated by the
element
![]() . Fill out the first column of
the above chart by saying how this element acts on each
irrep appearing in the Higgs and fermion reps. In each case
this element acts as multiplication by some number, so
just write down this number.
For example, the Higgs boson lives in the trivial rep of
. Fill out the first column of
the above chart by saying how this element acts on each
irrep appearing in the Higgs and fermion reps. In each case
this element acts as multiplication by some number, so
just write down this number.
For example, the Higgs boson lives in the trivial rep of
![]() , and
, and
![]() acts as multiplication by
acts as multiplication by
![]() on this rep, so you can write down `
on this rep, so you can write down `![]() ' for the Higgs.
' for the Higgs.
(We have not
listed the fermions of the second and third generations.
Since these transform in the same representations of ![]() as the fermions of the first generation, they are irrelevant
to the problem of finding the group
as the fermions of the first generation, they are irrelevant
to the problem of finding the group ![]() .)
.)
7. By Problem 5, the center of ![]() is generated
by the element
is generated
by the element
![]() . Fill out the
second column of the above chart by saying how this
element acts on each irrep in the Higgs and fermion reps.
In each case
this element acts as multiplication by some number, so
just write down this number. For example,
the Higgs boson lives in the defining rep of
. Fill out the
second column of the above chart by saying how this
element acts on each irrep in the Higgs and fermion reps.
In each case
this element acts as multiplication by some number, so
just write down this number. For example,
the Higgs boson lives in the defining rep of ![]() on
on ![]() , and
, and ![]() acts as multiplication by
acts as multiplication by ![]() on
this rep, so you can write down `
on
this rep, so you can write down `![]() ' for the Higgs.
' for the Higgs.
If you do Problems 6 and 7 correctly, you should
see that every number in the first two columns is a
sixth root of unity. So, to find elements of
![]() that act trivially on all reps in the Standard Model,
we only need to consider elements of
that act trivially on all reps in the Standard Model,
we only need to consider elements of ![]() that are
sixth roots of unity.
In other words, the subgroup
that are
sixth roots of unity.
In other words, the subgroup
![]() must be be contained in
must be be contained in
![]() .
.
8. Every
sixth root of unity is a power of
![]() .
So, fill out the third column of the above chart by saying how
this element acts on each irrep in the Higgs and fermion reps.
In each case
this element acts as multiplication by some number, so
just write down this number. For example, the Higgs boson
lives in the hypercharge-
.
So, fill out the third column of the above chart by saying how
this element acts on each irrep in the Higgs and fermion reps.
In each case
this element acts as multiplication by some number, so
just write down this number. For example, the Higgs boson
lives in the hypercharge-![]() rep of
rep of ![]() . In the hypercharge-
. In the hypercharge-![]() rep, each element
rep, each element
![]() acts as multiplication
by
acts as multiplication
by ![]() . Thus, for the Higgs, the element
. Thus, for the Higgs, the element
![]() acts as multiplication by
acts as multiplication by ![]() .
So, you can write down `
.
So, you can write down `![]() ' for the Higgs.
' for the Higgs.
9. What do you get when you multiply all 3 numbers in any row of the above chart?
10. Determine the group
![]() consisting of all elements that act as the identity
on the Higgs and fermion reps.
consisting of all elements that act as the identity
on the Higgs and fermion reps.
Hint: Problem 9 is an incredibly important clue.
The precise nature of the subgroup ![]() turns out to be
crucial in setting up grand unified theories of particle physics, because
while we have
turns out to be
crucial in setting up grand unified theories of particle physics, because
while we have
Unfortunately, this model predicts that a proton will eventually decay into a positron and neutral pion, with the mean lifetime of the proton being somewhere between 1026 and 1030 years. Experiments have shown that the proton lifetime is at least 5.5 x 1032 years -- no proton decay has ever been seen. So, people don't believe in the Georgi-Glashow model. Another beautiful theory killed by an ugly fact! But, this model serves as a basis for most other grand unified theories, so it's worth understanding.
![]()
![]()
Next: The
Eightfold Way
Previous: Hypercharge and Weak Isospin
© 2003 John Baez - all rights reserved.
baez@math.removethis.ucr.andthis.edu