August 16, 2006

This Week's Finds in Mathematical Physics (Week 238)

John Baez

NASA is trying to built up suspense with this "media advisory":

1) NASA, NASA Announces Dark Matter Discovery, http://www.nasa.gov/home/hqnews/2006/aug/HQ_M06128_dark_matter.html

which says simply:

Astronomers who used NASA's Chandra X-ray Observatory will host a media teleconference at 1 p.m. EDT Monday, Aug. 21, to announce how dark and normal matter have been forced apart in an extraordinarily energetic collision.

Someone nicknamed "riptalon" at Slashdot made a good guess. The media advisory lists the "briefing participants" as Maxim Markevitch, Doug Clowe and Sean Carroll. Markevitch and Clowe work with the Chandra X-ray telescope to study galaxy collisions and dark matter. Last November, Markevitch gave a talk on this work, which you can see here:

2) Maxim Markevitch, Scott Randall, Douglas Clowe, and Anthony H. Gonzalez, Insights on physics of gas and dark matter from cluster mergers, available at http://cxc.harvard.edu/symposium_2005/proceedings/theme_energy.html#abs23

So, barring any drastic new revelations, we can guess what's up. Markevitch and company have been studying the "Bullet Cluster", a bunch of galaxies that has a small bullet-shaped subcluster zipping away from the center at 4,500 kilometers per second. Here's a picture of it from the above paper:

To help you understand this picture a bit: the official name of the Bullet Cluster is 1E0657-56. The "exposure" for this X-ray photograph taken by Chanda was apparently 0.5 million seconds - 140 hours! The distance scale shown, 0.5 megaparsecs, is about 1.6 million light years. The cluster itself has a redshift z = 0.3, meaning its light has wavelengths stretched by a factor of 1.3. Under currently popular ideas on cosmology, this means it's roughly 4 billion light years away.

Anyway, what are we seeing here?

You can see rapidly moving galaxy cluster with a shock wave trailing behind it. It seems to have hit another cluster at high speed. When this kind of thing happens, the gas in the clusters is what actually collides - the individual galaxies are too sparse to hit very often. And when the gas collides, it gets hot. In this case, it heated up to about 160 million degrees and started emitting X-rays like mad! The picture shows these X-rays. This may be hottest known galactic cluster.

That's fun. But that's not enough reason to call a press conference. The cool part is not the crashing of gas against gas. The cool part is that the dark matter in the clusters was unstopped - it kept right on going!

How do people know this? Simple. Folks can see the gravity of the dark matter bending the light from more distant galaxies! It's called "gravitational lensing". Here are the mass density contours, as seen by this effect. I guess Clowe took this photo using the Hubble Space Telescope:

So: X-rays show the gas in one place, but gravity shows most of the mass is somewhere else - two lumps zipping along unstopped. That's good evidence that dark matter is for real.

For more try these:

3) M. Markevitch, S. Randall, D. Clowe, A. Gonzalez, and M. Bradac, Dark matter and the Bullet Cluster, available at http://www.cosis.net/abstracts/COSPAR2006/02655/COSPAR2006-A-02655.pdf

4) M. Markevitch, A. H. Gonzalez, D. Clowe, A. Vikhlinin, L. David, W. Forman, C. Jones, S. Murray, and W. Tucker, Direct constraints on the dark matter self-interaction cross-section from the merging galaxy cluster 1E0657-56, available as arXiv:astro-ph/0309303.

5) Maxim Markevitch, Chandra observation of the most interesting cluster in the Universe, available as arXiv:astro-ph/0511345.

6) M. Markevitch, A. H. Gonzalez, L. David, A. Vikhlinin, S. Murray, W. Forman, C. Jones and W. Tucker, A textbook example of a bow shock in the merging galaxy cluster 1E0657-56, Astrophys. J. 567 (2002), L27. Also available as arXiv:astro-ph/0110468.

7) Eric Hayashi and Simon D. M. White, How rare is the Bullet Cluster?, Mon. Not. Roy. Astron. Soc. Lett. 370 (2006), L38-L41, available as arXiv:astro-ph/0604443.

The first of these is, alas, only the abstract of a talk. But it's worth reading, so I'll quote it in its entirety here:

1E0657-56, the "Bullet Cluster", is a merger with a uniquely simple geometry. From the long Chandra X-ray observation which revealed a classic bow shock in front of a small subcluster, we can derive the velocity of the subcluster and its direction of motion. Recent accurate weak and strong lensing total mass maps clearly show two merging subclusters, including the host of the gas bullet seen in X-rays. This cluster provided the first direct, model-independent proof of the dark matter existence (as opposed to any modified gravity theory) and a direct constraint on the self-interaction cross-section of the dark matter particles. I will review these and other related results.

The Bullet Cluster is not the only direct evidence for dark matter. In fact, last year folks claimed to have found a "ghost galaxy" made mainly of dark matter and cold hydrogen, with very few stars:

8) PPARC, New evidence for a dark matter galaxy, http://www.interactions.org/cms/?pid=1023641

However, Matt Owers informs me that the consensus on this ghost, VIRGOHI 21, is that it's hydrogen stripped off from a galaxy by the "wind" it felt as it fell into the Virgo Cluster. This effect is called "ram pressure stripping" - the gas of a galaxy can be stripped off if the galaxy is moving rapidly through a cluster, due to interaction with the gas in the cluster.

Nonetheless, dark matter is seeming more and more real. It thus becomes ever more interesting to find out what dark matter actually is. The lightest neutralino? Axions? Theoretical physicists are good at inventing plausible candidates, but finding them is another thing.

Since I'd like to send this off in time to beat NASA, I won't say a lot more today... just a bit.

Dan Christensen and Igor Khavkine have discovered some fascinating things by plotting the amplitude of the tetrahedral spin network - the basic building block of spacetime in 3d quantum gravity - as a function of the cosmological constant.

They get pictures like this:

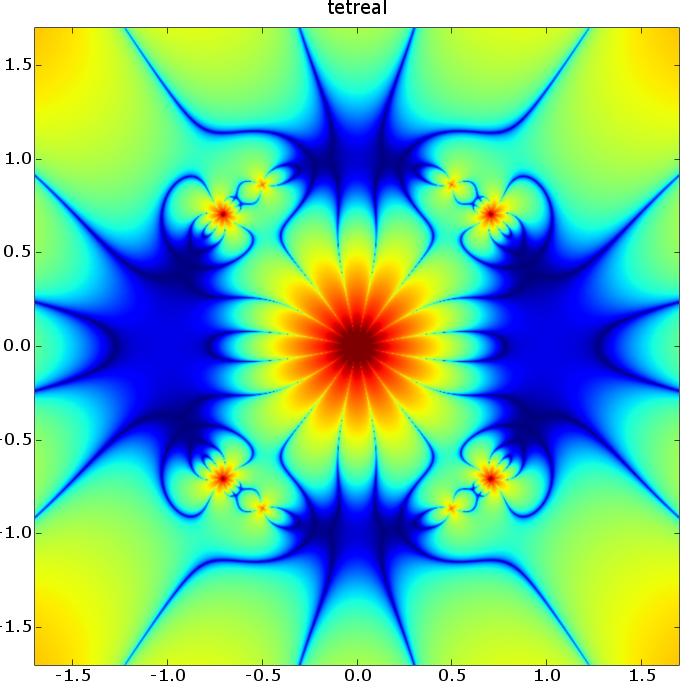
9) Dan Christensen and Igor Khavkine, Plots of q-deformed tets, http://jdc.math.uwo.ca/spinnet/

Here the color indicates the real part of the spin network amplitude, and it's plotted as a function of q, which is related to the cosmological constant by a funky formula I won't bother to write down here.

You can get some nice books on category theory for free these days:

10) Jiri Adamek, Horst Herrlich and George E. Strecker, Abstract and Concrete Categories: the Joy of Cats, available at http://katmat.math.uni-bremen.de/acc/acc.pdf

11) Robert Goldblatt, Topoi: the Categorial Analysis of Logic, available at http://cdl.library.cornell.edu/cgi-bin/cul.math/docviewer?did=Gold010

12) Michael Barr and Charles Wells, Toposes, Triples and Theories, available at http://www.case.edu/artsci/math/wells/pub/ttt.html

The first two are quite elementary - don't be scared of the title of Goldblatt's book; the only complaints I've ever heard about it boil down to the claim that it's too easy!

You can also download this classic text on synthetic differential geometry, which is an approach to differential geometry based on infinitesimals, formalized using topos theory:

13) Anders Kock, Synthetic Differential Geometry, available at http://home.imf.au.dk/kock/

He asks that we not circulate it in printed form - electrons are okay, but not paper.

Next I want to say a tiny bit about Koszul duality for Lie algebras, which plays a big role in the work of Castellani on the M-theory Lie 3-algebra, which I discussed in "week237".

Let's start with the Maurer-Cartan form. This is a gadget that shows up in the study of Lie groups. It works like this. Suppose you have a Lie group G with Lie algebra Lie(G). Suppose you have a tangent vector at any point of the group G. Then you can translate it to the identity element of G and get a tangent vector at the identity of G. But, this is nothing but an element of Lie(G)!

So, we have a god-given linear map from tangent vectors on G to the Lie algebra Lie(G). This is called a "Lie(G)-valued 1-form" on G, since an ordinary 1-form eats tangent vectors and spits out numbers, while this spits out elements of Lie(G). This particular god-given Lie(G)-valued 1-form on G is called the "Maurer-Cartan form", and denoted ω.

Now, we can define exterior derivatives of Lie(G)-valued differential forms just as we can for ordinary differential forms. So, it's interesting to calculate d ω and see what it's like.

The answer is very simple. It's called the Maurer-Cartan equation:

dω = -½ ω ^ ω

On the right here I'm using the wedge product of Lie(G)-valued differential forms. This is defined just like the wedge product of ordinary differential forms, except instead of multiplication of numbers we use the bracket in our Lie algebra.

I won't prove the Maurer-Cartan equation; the proof is so easy you can even find it on the Wikipedia:

14) Wikipedia, Maurer-Cartan form, http://en.wikipedia.org/wiki/Maurer-Cartan_form

An interesting thing about this equation is that it shows everything about the Lie algebra Lie(G) is packed into the Maurer-Cartan form. The reason is that everything about the bracket operation is packed into the definition of ω ^ ω.

If you have trouble seeing this, note that we can feed ω ^ ω a pair of tangent vectors at any point of G, and it will spit out an element of Lie(G). How will it do this? The two copies of ω will eat the two tangent vectors and spit out elements of Lie(G). Then we take the bracket of those, and that's the final answer.

Since we can get the bracket of any two elements of Lie(G) using this trick, ω ^ ω knows everything about the bracket in Lie(G). You could even say it's the bracket viewed as a geometrical entity - a kind of "field" on the group G!

Now, since

dω = -½ ω ^ ω

and the usual rules for exterior derivatives imply that

d²ω = 0

we must have

d(ω ^ ω) = 0

If we work this concretely what this says, we must get some identity involving the bracket in our Lie algebra, since ω ^ ω is just the bracket in disguise. What identity could this be?

THE JACOBI IDENTITY!

It has to be, since the Jacobi identity says there's a way to take 3 Lie algebra elements, bracket them in a clever way, and get zero:

[u,[v,w]] + [v,[w,u]] + [w,[u,v]] = 0

while d(ω ^ ω) is a Lie(G)-valued 3-form that happens to vanish, built using the bracket.

It also has to be since the equation d² = 0 is just another way of saying the Jacobi identity. For example, if you write out the explicit grungy formula for d of a differential form applied to a list of vector fields, and then use this to compute d² of that differential form, you'll see that to get zero you need the Jacobi identity for the Lie bracket of vector fields. Here we're just using a special case of that.

The relationship between the Jacobi identity and d² = 0 is actually very beautiful and deep. The Jacobi identity says the bracket is a derivation of itself, which is an infinitesimal way of saying that the flow generated by a vector field, acting as an operation on vector fields, preserves the Lie bracket! And this, in turn, follows from the fact that the Lie bracket is preserved by diffeomorphisms - in other words, it's a "canonically defined" operation on vector fields.

Similarly, d² = 0 is related to the fact that d is a natural operation on differential forms - in other words, that it commutes with diffeomorphisms. I'll leave this cryptic; I don't feel like trying to work out the details now.

Instead, let me say how to translate this fact:

into pure algebra. We'll get something called "Kozsul duality". I always found Koszul duality mysterious, until I realized it's just a generalzation of the above fact.

How can we state the above fact purely algebraically, only using the Lie algebra Lie(G), not the group G? To get ourselves in the mood, let's call our Lie algebra simply L.

By the way we constructed it, the Maurer-Cartan form is "left-invariant", meaning it doesn't change when you translate it using maps like this:

Lg: G → G
    x |→ gx

that is, left multiplication by any element g of G. So, how can we describe the left-invariant differential forms on G in a purely algebraic way? Let's do this for ordinary differential forms; to get Lie(G)-valued ones we can just tensor with L = Lie(G).

Well, here's how we do it. The left-invariant vector fields on G are just

L

so the left-invariant 1-forms are

L*

So, the algebra of all left-invariant diferential forms on G is just the exterior algebra on L*. And, defining the exterior derivative of such a form is precisely the same as giving the bracket in the Lie algebra L! And, the equation d² = 0 is just the Jacobi identity in disguise.

To be a bit more formal about this, let's think of L as a graded vector space where everything is of degree zero. Then L* is the same sort of thing, but we should add one to the degree to think of guys in here as 1-forms. Let's use S for the operation of "suspending" a graded vector space - that is, adding one to the degree. Then the exterior algebra on L* is the "free graded-commutative algebra on SL*".

So far, just new jargon. But this lets us state the observation of the penultimate paragraph in a very sophisticated-sounding way. Take a vector space L and think of it as a graded vector space where everything is of degree zero. Then:

Making the free graded-commutative algebra on SL* into a differential graded-commutative algebra is the same as making L into a Lie algebra.

Making the free graded Lie algebra on SL* into a differential graded Lie algebra is the same as making L into a commutative algebra.

So, we say the concepts "Lie algebra" and "commutative algebra" are Koszul dual. Interestingly, the concept "associative algebra" is its own dual:

Making the free graded associative algebra on SL* into a differential graded associative algebra is the same as making L into an associative algebra.

This is the beginning of a big story, and I'll try to say more later. If you get impatient, try the book on operads mentioned in "week191", or else these:

15) Victor Ginzburg and Mikhail Kapranov, Koszul duality for quadratic operads, Duke Math. J. 76 (1994), 203-272. Also Erratum, Duke Math. J. 80 (1995), 293.

16) Benoit Fresse, Koszul duality of operads and homology of partition posets, Homotopy theory and its applications (Evanston, 2002), Contemp. Math. 346 (2004), 115-215. Also available at http://math.univ-lille1.fr/~fresse/PartitionHomology.html

The point is that Lie, commutative and associative algebras are all defined by "quadratic operads", and one can define for any such operad O a "dual" operad O* such that:

Making the free graded O-algebra on SL* into a differential graded O-algebra is the same as making L into an O*-algebra.

And, we have O** = O, hence the term "duality".

This has always seemed incredibly cool and mysterious to me. There are other meanings of the term "Koszul duality", and if really understood them I might better understand what's going on here. But, I'm feeling happy now because I see this special case:

Making the free graded-commutative algebra on SL* into a differential graded-commutative algebra is the same as making L into a Lie algebra.

is really just saying that the exterior derivative of left-invariant differential forms on a Lie group encodes the bracket in the Lie algebra. That's something I have a feeling for. And, it's related to the Maurer-Cartan equation... though notice, I never completely spelled out how.

Addenda: Let me say some more about how d² = 0 is related to the fact that d is a canonically defined operation on differential forms. Being "canonically defined" means that d commutes with the action of diffeomorphisms. Saying that d commutes with "small" diffeomorphisms - those connected by a path to the identity - is the same as saying

d L_v = L_v d

where v is any vector field and L_v is the corresponding "Lie derivative" operation on differential forms. But, Weil's formula says that

L_v = i_v d + d i_v

where i_v is the "interior product with v", which sends p-forms to (p-1)-forms. If we plug Weil's formula into the equation we're pondering, we get

d (i_v d + d i_v) = (i_v d + d i_v) d

which simplifies to give

d² i_v = i_v d²

So, as soon as we know d² = 0, we know d commutes with small diffeomorphisms. Alas, I don't see how to reverse the argument.

Similarly, as soon as we know the Jacobi identity, we know the Lie bracket operation on vector fields is preserved by small diffeomorphisms, by the argument outlined in the body of this Week. This argument is reversable.

So, maybe it's an exaggeration to say that d² = 0 and the Jacobi identity say that d and the Lie bracket are preserved by diffeomorphisms - but at least they imply these operations are preserved by small diffeomorphisms.

© 2006 John Baez
baez@math.removethis.ucr.andthis.edu