week237

August 10, 2006

This Week's Finds in Mathematical Physics (Week 237)

John Baez

This Week I'd like to talk about math books in Shanghai, and Urs Schreiber's blog entry on the gauge 3-group of M-theory. But first:

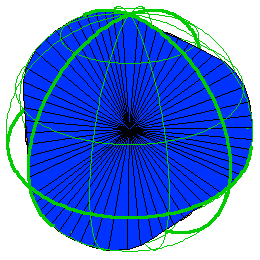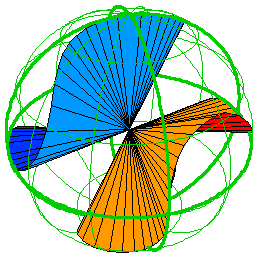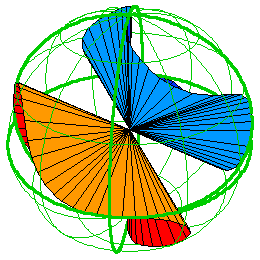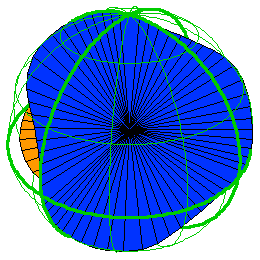
1) Greg Egan, Klein's quartic equation, http://gregegan.customer.netspace.net.au/SCIENCE/KleinQuartic/KleinQuarticEq.html

I discussed Klein's quartic curve in "week214" and "week215". The idea is to take the nontrivial complex solutions of

u³ v + v³ w + w³ u = 0

and "projectivize" them - in other words, count two as the same if one is just a multiple of the other:

(u',v',w') = c(u,v,w)

The result is a 3-holed Riemann surface with the maximum number of symmetries! Here by a "symmetry" I mean a conformal transformation mapping the surface to itself. Back in 1893 Hurwitz proved something quite bizarre: an n-holed Riemann surface can't have more than 84(n-1) symmetries if n > 1. So, a 3-holed Riemann surface can't have more than 168 symmetries - and Klein's quartic curve has exactly that many!

These 168 symmetries were constructed by Klein way back in 1879, but Egan gives an elementary proof that uses only algebra and a bit of calculus... and a lot of cleverness. And, his page has a wonderful spinning picture of the real solutions of

u³ v + v³ w + w³ u = 0.

This is what you see above.

As you can see, it consists of lots of lines through the origin, including the u, v, and w axes. When we "projectivize", we get one point for each of these lines, so we get a curve which is the real version of Klein's quartic curve. This curve has an obvious 3-fold symmetry, from cyclically permuting the coordinate axes. The rest of the 168 symmetries are only easy to visualize when we go to the complex version - as Egan explains.

It's great that Egan can draw this thing in Perth and I can easily see it my apartment here in Shanghai - I feel like I'm living in a futuristic world, and I'm only 45. What it'll be like when I'm 64?

Another pleasant thing about life in Shanghai, at least for a well-off visitor from America, is how cheap everything is. It's clear why the US is running an enormous trade deficit: there's a vast economic differential. Stopping the flow of goods one way and dollars the other would be like damming the Niagara Falls.

For example, last night I saw this excellent hardcover book on sale for 78 yuan, or about $10:

2) Yu. I. Manin and A. A. Panchishkin, Introduction to Modern Number Theory, second edition, Science Press, 2005.

It's a great overview of number theory, from the basics through class field theory to L-functions, modular forms and the Langlands program! It's wisely divided into three sections: "problems and tricks", "ideas and theories", and "analogies and visions". Back when I used to hate number theory, I thought it was all problems and tricks. Now I'm beginning to learn some of the ideas and theories, and I hope eventually to grasp the analogies and visions discussed here - for example, the analogy between Arakelov geometry and noncommutative geometry.

$10 is a nice price for a math book. If you buy this one from Springer Verlag, you'll pay ten times that. Illegal knockoffs of Western books are common in China, but I think the one I saw is legal, since Springer has signed an agreement with Science Press, which is run by the Chinese Academy of Sciences. In exchange for letting Science Press publish Springer books in China at affordable prices, Springer gets to publish translations of Chinese journals in the West at unaffordable prices.

By the way - after checking out the bookstore, I went out to the street vendors and bought an excellent dinner of rice, sausage and vegetables for 35 yuan - about 40 cents US. It was cooked by a husband and wife in a wok on a cart.

Just after I bought it, someone yelled the Chinese equivalent of "cops!", and all the street vendors suddenly dashed away with their carts, leaving only the woman, who kindly handed me my dinner in a styrofoam pack before walking off. They clearly had this down to a fine art: it all happened faster than my brain could process. I guess the cops don't allow street vendors there.

I only wish I'd noticed: did the street vendors turn off their gas stoves before running, or run while still cooking?

Anyway, on to some serious math and physics.

You've probably heard of some mysterious thing called "M-theory" that lives in 11 dimensions. Back in "week158" and "week159" I took a stab at understanding this. Now I'll try again, with a lot of help from Urs Schreiber:

3) Urs Schreiber, Castellani on free differential algebras in supergravity: gauge 3-group of M-theory, http://golem.ph.utexas.edu/string/archives/000840.html

Calling M-theory a "theory" is a bit misleading, because nobody knows what this theory is! There's just a lot of clues pointing to its existence. It seems to be the quantum version of a well-defined classical field theory called "11-dimensional supergravity". And, it seems to involve 2-branes and 5-branes: 2- and 5-dimensional membranes that trace out 3- and 6-dimensional surfaces in spacetime, just like strings trace out 2-dimensional surfaces.

Back in "week158" I wrote down a Lagrangian for 11d supergravity. This is a truly monstrous thing involving three fields:

A) a frame field e - the "graviton",

B) a field ψ taking values in the real spin-3/2 representation of the 11d Lorentz group - the "gravitino",

C) a 3-form A.

When it was discovered back in 1978, people were interested in 11d supergravity mainly because it was the highest-dimensional theory they could concoct that includes general relativity and supersymmetry - a symmetry that interchanges bosons and fermions, in this case gravitons and gravitinos - without including any particles of spin > 2. So, the fact that it looked like a mess wasn't such a big deal. But now that some people are taking it very seriously, it's worth trying to understand the math behind it more deeply, to see what makes it tick.

For example: what's so great about 11 dimensions? And: what's the reason for that 3-form?

I'm not a huge fan of string theory, but I like puzzles of this sort - finding patterns that make certain things work only in certain dimensions, and stuff like that. So, I got intrigued when I learned that super-Yang-Mills theory and superstring theory are nice in dimension 10 because of special properties of the octonions - see "week104". Maybe a little extra stretch could bring us to dimension 11?

I got even more intrigued when I ran across two competing explanations for that 3-form in 11d supergravity. One was that it's a connection on a twice categorified version of a U(1) bundle. The other was that it's the Chern-Simons form for an E₈ gauge theory.

Let me say a bit about what these means. I talked about categorified U(1) bundles in "week210", so I'll be sort of brief about those....

A connection on a U(1)-bundle looks locally like a 1-form, so we can integrate it along a path and compute how the phase of charged particle changes when we move it along that path:

             f
  x------------>-----y    a path f from the point x to the point y:
                                 we write this as f: x → y

Believe it or not, this is the basis of all modern ideas on electromagnetism!

If we categorify this whole idea once, we get a kind of connection that looks locally like a 2-form. Folks call this a "connection on a U(1) gerbe", but don't let the use of French here intimidate you: they just do that so they can charge more for the wine. It's just a gadget that you can integrate over a surface, to compute how the phase of a charged string moves when we slide it along that surface:

              f
    ----------->-----
   /        ||       \
  x         ||F       y   a path-of-paths F from the path f to the path g:
   \        \/       /            we write this as F: f => g
    ----------->-----
               g

And, if we categorify once more, we get a "connection on a U(1) 2-gerbe". This is something that looks locally like a 3-form, which describes what happens when we move 2-branes around!

If you're wondering why I'm talking about "categorifying", it's because this:

             f
  x------------>-----y

is also a picture of a morphism in a category, while this:

              f
    ----------->-----
   /        ||       \
  x         ||F       y  
   \        \/       /  
    ----------->-----
               g

is a picture of a 2-morphism in a 2-category and so on. We're talking about processes between processes between processes... so we're climbing up the ladder of n-categories.

Anyway: since 11d supergravity has a 3-form in it, and M-theory apparently has 2-branes in it, maybe we need to categorify the concept of a U(1) bundle twice to understand what's going on here!

I came up with this crazy idea on my own back in "week158", but it's an obvious guess after you learn that the 2-form field called B in 10d superstring theory really is a connection on a U(1) gerbe:

4) Alan L. Carey, Stuart Johnson and Michael K. Murray, Holonomy on D-branes, available as arXiv:hep-th/0204199.

Unfortunately there are some problems with naively pushing this idea up a dimension. For example, a crucial factor of 1/6 in the Lagrangian for 11d supergravity is not explained by thinking of A this way.

Another possible explanation was that this 3-form is the Chern-Simons form of an E₈ bundle over spacetime:

5) Emanuel Diaconescu, Gregory Moore and Edward Witten, E₈ gauge theory, and a derivation of K-theory from M-theory, Adv. Theor. Math. Phys. 6 (2003) 1031-1134. Also available as arXiv:hep-th/0005090.

6) Emanuel Diaconescu, Daniel S. Freed and Gregory Moore, The M-theory 3-form and E₈ gauge theory, available as arXiv:hep-th/0312069.

This idea explains that factor of 1/6. And, it might move towards an explanation of how the octonions get into the act, because the group E₈ is deeply related to the octonions. But as the authors of the above paper say, "the E₈ gauge field plays a purely topological role and appears, in some sense, to be a 'fake'." In particular, you don't see any E₈ connection staring you in the face in the Lagrangian for 11d supergravity that I wrote down in "week158".

Later, it started becoming clear that both ideas - the twice categorified U(1) connection and the E₈ gauge theory - fit together in some way:

7) Paolo Aschieri and Branislav Jurco, Gerbes, M5-brane anomalies and E₈ gauge theory, JHEP 0410 (2004), 068. Also available as arXiv:hep-th/0409200.

It all became a lot clearer to me when Urs Schreiber read these papers and translated them into a language I like:

8) Leonardo Castellani, Lie derivatives along antisymmetric tensors, and the M-theory superalgebra, available as arXiv:hep-th/0508213.

9) Pietro Fré and Pietro Antonio Grassi, Pure spinors, free differential algebras, and the supermembrane, available as arXiv:hep-th/0606171.

The idea is to think of 11d supergravity as a twice categorifed gauge theory - not just the 3-form field in 11d supergravity, but all the fields, in a unified way!

For this, we need to do something much more clever than taking 11d spacetime and slapping a U(1) 2-gerbe on top of it. We need to combine the graviton, the gravitino and the 2-form field into a connection on a nonabelian 2-gerbe.

Here things get a bit technical, but Urs has covered the technical points quite nicely in his blog, so right now I'll just try to give you some hand-wavy intuitions.

Very roughly speaking, an connection on a bundle takes any path in spacetime

             f
  x------------>-----y

and gives you an element of some group, which says how a particle would transform if you moved it along this path. This group could be U(1) - the group of phases - or it could be something more fun, like a nonabelian group.

If we categorify this concept, we get the concept of a connection on a "2-bundle" (which is more or less the same as a gerbe). Such a connection takes any path and gives you an object in some 2-group, but it also takes any surface like this:

              f
    ----------->-----
   /        ||       \
  x         ||F       y  
   \        \/       /  
    ----------->-----
               g

and gives you a morphism in this 2-group. You see, 2-group is a kind of category that acts like a group, and a category has "objects" and "morphisms". The morphisms go between objects. For more on 2-groups, try:

10) Higher-dimensional algebra V: 2-Groups, with Aaron D. Lauda, Theory and Applications of Categories 12 (2004), available at http://www.tac.mta.ca/tac/volumes/12/14/12-14abs.html Also available as math.QA/0307200.

If we categorify once more, we get connections on a "3-bundle", which is more or less the same thing as a "2-gerbe" - unfortunately the numbering systems are off by one. This gives us objects, morphisms and 2-morphisms in a 3-group, which describe what happens when we move particles, strings and 2-branes.

And so on:

group         point particles
2-group       point particles and strings
3-group       point particles, strings and 2-branes
4-group       point particles, strings, 2-branes and 3-branes

etc.

So, if 11d supergravity is a twice categorified gauge theory, we need to know its symmetry 3-group.

But actually, since we're doing geometry, this 3-group should be a "Lie 3-group". In other words, very roughly speaking, a 3-group that has a manifold of objects, a manifold of morphisms, and a manifold of 2-morphisms, where all the operations are smooth.

But actually, since we're doing supersymmetric geometry, we need a "Lie 3-supergroup"! In other words, very roughly speaking, a 3-group that has a supermanifold of objects, a supermanifold of morphisms, and a supermanifold of 2-morphisms, where all the operations are smooth. (Maybe I should say "supersmooth", just to be consistent.)

If you don't know what a supermanifold is, now is probably not the time to learn. I mean, not right this second. The point is just this: supersymmetry infests everything once you let it in the door, just like n-categories, and just like manifolds - and now we're doing all three.

In fact, nobody has even written down a rigorous definition of a Lie 3-supergroup yet! But, Lie algebras are in some ways simpler than Lie groups, and they're a good start, so we can be glad that people do know what a Lie 3-superalgebra is!

And Urs describes, in his blog, the relevant Lie 3-superalgebra for 11d supergravity!

I would like to say more about this, but it's getting a bit tough trying to talk about this stuff in a fun, easily accessible style, and I have the feeling I'm no longer succeeding. In fact, I don't think I can give a "fun, easily accessible" description of this specific Lie 3-superalgebra - at least not yet. So, now I'll completely give up trying to be comprehensible, and simply state some facts.

As shown here:

11) Higher-dimensional algebra VI: Lie 2-Algebras, with Alissa Crans, Theory and Applications of Categories 12 (2004), available at http://www.tac.mta.ca/tac/volumes/12/15/12-15abs.html Also available as math.QA/0307200.

the category of Lie n-algebras is equivalent to the category of L_∞ algebras which as chain complexes have only n nonvanishing terms, the 0th to the (n-1)st. L_∞ algebras are just algebras of Stasheff's L_∞ operad in the category of chain complexes of vector spaces - see "week191" and especially these:

12) Martin Markl, Steve Schnider and Jim Stasheff, Operads in Algebra, Topology and Physics, AMS, Providence, Rhode Island, 2002.

James Stasheff, Hartford/Luminy talks on operads, available at http://www.math.unc.edu/Faculty/jds/operadchik.ps

But, we can replace vector spaces by Z/2-graded vector spaces and everything still works. Physicists call Z/2-graded vector spaces "super vector spaces". So, a "Lie n-superalgebra" is an algebra of the L_∞ operad in the category of chain complexes of super vector spaces.

Given this, to specify a Lie 3-superalgebra we first need to specify the 0-chains, then the 1-chains, then the 2-chains.

For the particular one Urs mentions, we have

{0-chains} = 11d Poincaré Lie superalgebra
{1-chains} = {0}
{2-chains} = R

Here R is the real numbers, and this 1-dimensional thing is what ultimately gives the 3-form field A in 11d supergravity. As a vector space, the 11d Poincaré Lie superalgebra is the direct sum of an even part, which is the usual Poincaré Lie algebra iso(11,1), and an odd part, which is the 32-dimensional real spinor rep of so(11,1). These give the graviton (or more precisely the Levi-Civita connection) and the gravitino in 11d supergravity.

Next we need to make this stuff into a chain complex. That's easy: the differential has to be zero.

Next, we need to specify the L_∞ structure on this chain complex. First, we need a binary bracket operation, like in an ordinary Lie superalgebra. The bracket of 0-chains is the usual bracket in the 11d Poincaré Lie superalgebra. All the other binary brackets are zero.

Then, we need a ternary bracket operation, which expresses how the Jacobi identity holds only up to chain homotopy. This is zero.

Then, we need a quaternary bracket operation (since that chain homotopy satisfies its own identity only up to chain homotopy). This is nonzero: when we take the quaternary bracket of four 0-chains we get a 2-chain, and there's a nontrivial way to define this! This is the interesting bit, since ultimately it relates the graviton/gravitino to the 3-form field.

How do we get that quaternary bracket? Well, here's where things get funky: D'Auria and Fré dreamt up a formula that gives a number from 2 spinors and 2 vectors:

(ψ, φ, v, w) |→ ψ* Γ^ab φ v_a w_b

where that "ψ*" should really be "ψ-bar". And, magically, in 11 dimensions this gives a 4-cocycle on the Poincaré Lie superalgebra! The proof of this uses some Fierz identity in 11 dimensions:

12) R. D'Auria and Pietro Fré, Geometric supergravity in D = 11 and its hidden supergroup, Nucl. Phys. B201 (1982), 101-140. Also available at http://www.math.uni-hamburg.de/home/schreiber/sdarticle.pdf

And, from HDA6 we know that the 4-cocycle condition is just what's needed to make the quaternary bracket satisfy the identity we need for a Lie 3-superalgebra. (Alissa and I just did the calculation for Lie n-algebras, but the "super" stuff should work too with a few signs thrown in.)

So, this is all very cool, but I need to understand Fierz identities in different dimensions to see what if anything is special to 11d here - or, alternatively, work out the cohomology of Poincaré Lie superalgebras, to see when they can be deformed to Lie n-superalgebras. Sounds like a lot of work - maybe someone already did it. Actually D'Auria and Fre make it look like a matter of understanding tensor products of irreps of so(n,1), which is not bad. A worthwhile project in any event.

I also need to understand what all this has to do with E₈. For that the paper by Diaconescu, Freed and Moore should help.

Well, this is just the beginning, but Urs explains the rest.

Addenda: I thank Noam Elkies for a correction. Aaron Bergman has this to say about E₈ and M-theory:

John Baez wrote:
> I also need to understand what all this has to do with E₈.
E₈ might not have much of anything to do with this. As mentioned in Diaconescu, Freed and Moore, E₈ appears to function solely as a convenient stand-in for K(Z,3).
On the other hand, the split form of the E-series (up to E₁₁ if you're feeling particularly speculative) is known to show up in describing the fields of 11D SUGRA, but the I don't think anyone knows of a connection between the two E₈s. Just to add to the fun, E₈ gauge fields also show up on the fixed points of M-theory on S¹/Z₂ giving the E₈ × E₈ heterotic string.
Aaron

Urs Schreiber replied:

Aaron Bergman wrote:
 > E₈ gauge fields also show up on the fixed points of 
 > M-theory on S¹/Z₂ giving the E₈ × E₈ heterotic string.
The topological part of the membrane action involves the integral of the sugra 3-form over the worldvolume. By DFW, part of that 3-form can be thought of as an E₈ CS 3-form.
So part of the membrane action looks similar to an E₈ CS-theory over the worldvolume.
Now let the membrane have a boundary. A bulk E₈ CS-theory is well known to induce an E₈ WZW theory on the boundary.
Could this be the connection between the DWF E₈ and the Horava-Witten E₈?
I have asked this question before: http://golem.ph.utexas.edu/string/archives/000791.html. Jarah then agreed that this must be about right. But it is not completely clear to me yet.
One problem is that in CS-theory we vary the connection, while in the topological membrane the E₈ connection on the background is fixed and we vary the embedding by which we pull it back to the worldvolume. Under suitable assumptions that might be equivalent to varying an E₈ connection on the worldvolume itself?

Aaron Bergman replied:

Urs Schreiber wrote:
 > Now let the membrane have a boundary. A bulk E₈ CS-theory is
 > well known to induce an E₈ WZW theory on the boundary.
 >
 > Could this be the connection between the DWF E₈ and the
 > Horava-Witten E₈?
A similar observation was made by Horava way back in arXiv:hep-th/9712130 (in the final section).
Aaron