July 26, 2006

This Week's Finds in Mathematical Physics (Week 236)

John Baez

This week I'd like to catch you up on some papers about categorification and quantum mechanics.

But first, since it's summer vacation, I'd like to take you on a little road trip - to infinity. And then, for fun, a little detective story about the history of the icosahedron.

Cantor invented two kinds of infinities: cardinals and ordinals. Cardinals are more familiar. They say how big sets are. Two sets can be put into 1-1 correspondence iff they have the same number of elements - where this kind of "number" is a cardinal.

But today I want to talk about ordinals. Ordinals say how big "well-ordered" sets are. A set is well-ordered if it's linearly ordered and every nonempty subset has a smallest element.

For example, the empty set

{}

is well-ordered in a trivial sort of way, and the corresponding ordinal is called

0.

Similarly, any set with just one element, like this:

{0}

is well-ordered in a trivial sort of way, and the corresponding ordinal is called

1.

Similarly, any set with two elements, like this:

{0,1}

becomes well-ordered as soon as we decree which element is bigger; the obvious choice is to say 0 < 1. The corresponding ordinal is called

2.

Similarly, any set with three elements, like this:

{0,1,2}

becomes well-ordered as soon as we linearly order it; the obvious choice here is to say 0 < 1 < 2. The corresponding ordinal is called

3.

Perhaps you're getting the pattern - you've probably seen these particular ordinals before, maybe sometime in grade school. They're called finite ordinals, or "natural numbers".

But there's a cute trick they probably didn't teach you then: we can define each ordinal to be the set of all ordinals less than it:

0 = {}            (since no ordinal is less than 0) 
1 = {0}           (since only 0 is less than 1)  
2 = {0,1}         (since 0 and 1 are less than 2)
3 = {0,1,2}       (since 0, 1 and 2 are less than 3)

Now, what comes after all the finite ordinals? Well, the set of all finite ordinals is itself well-ordered:

{0,1,2,3,...}

So, there's an ordinal corresponding to this - and it's the first infinite ordinal. It's usually called omega (ω). Using the cute trick I mentioned, we can actually define

ω = {0,1,2,3,...}

Now, what comes after this? Well, it turns out there's a well-ordered set

{0,1,2,3,...,ω}

containing the finite ordinals together with ω, with the obvious notion of "less than": ω is bigger than the rest. Corresponding to this set there's an ordinal called

ω+1

As usual, we can simply define

ω+1 = {0,1,2,3,...,ω}

(At this point you could be confused if you know about cardinals, so let me throw in a word of reassurance. The sets ω and ω+1 have the same "cardinality", but they're different as ordinals, since you can't find a 1-1 and onto function between them that preserves the ordering. This is easy to see, since ω+1 has a biggest element while ω does not.)

Now, what comes next? Well, not surprisingly, it's

ω+2 = {0,1,2,3,...,ω,ω+1}

Then comes

ω+3, ω+4, ω+5,...

and so on. You get the idea.

What next?

Well, the ordinal after all these is called ω+ω. People often call it "ω times 2" or "ω2" for short. So,

ω2 = {0,1,2,3,...,ω,ω+1,ω+2,ω+3,....}

What next? Well, then comes

ω2 + 1, ω2 + 2,...

and so on. But you probably have the hang of this already, so we can skip right ahead to ω3.

In fact, you're probably ready to skip right ahead to ω4, and ω5, and so on.

In fact, I bet now you're ready to skip all the way to "ω times ω", or ω² for short:

ω² = {0,1,2...ω,ω+1,ω+2,...,ω2,ω2+1,ω2+2,...}

It would be fun to have a book with ω pages, each page half as thick as the previous page. You can tell a nice long story with an ω-sized book. But it would be even more fun to have an encyclopedia with ω volumes, each being an ω-sized book, each half as thick as the previous volume. Then you have ω² pages - and it can still fit in one bookshelf!

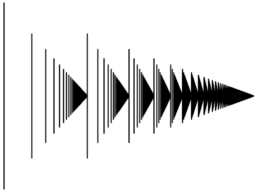
What comes next? Well, we have

ω²+1, ω²+2, ...

and so on, and after all these come

ω²+ω, ω²+ω+1, ω²+ω+2, ...

and so on - and eventually

ω² + ω² = ω² 2

and then a bunch more, and then

ω² 3

and then a bunch more, and then

ω² 4

and then a bunch more, and more, and eventually

ω² ω = ω³.

You can probably imagine a bookcase containing ω encyclopedias, each with ω volumes, each with ω pages, for a total of ω³ pages.

I'm skipping more and more steps to keep you from getting bored. I know you have plenty to do and can't spend an infinite amount of time reading This Week's Finds, even if the subject is infinity.

So, if you don't mind me just mentioning some of the high points, there are guys like ω⁴ and ω⁵ and so on, and after all these comes

ω^ω.

And then what?

Well, then comes ω^ω + 1, and so on, but I'm sure that's boring by now. And then come ordinals like

ω^ω 2,..., ω^ω 3, ..., ω^ω 4, ...

leading up to

ω^ω ω = ω^{ω + 1}

Then eventually come ordinals like

ω^ω ω² , ..., ω^ω ω³, ..., ω^ω ω⁴, ...

and so on, leading up to:

ω^ω ω^ω = ω^{ω + ω} = ω^{ω 2}

This actually reminds me of something that happened driving across South Dakota one summer with a friend of mine. We were in college, so we had the summer off, so we drive across the country. We drove across South Dakota all the way from the eastern border to the west on Interstate 90.

This state is huge - about 600 kilometers across, and most of it is really flat, so the drive was really boring. We kept seeing signs for a bunch of tourist attractions on the western edge of the state, like the Badlands and Mt. Rushmore - a mountain that they carved to look like faces of presidents, just to give people some reason to keep driving.

Anyway, I'll tell you the rest of the story later - I see some more ordinals coming up:

ω^ω3,... ω^ω4,... ω^ω5,...

We're really whizzing along now just to keep from getting bored - just like my friend and I did in South Dakota. You might fondly imagine that we had fun trading stories and jokes, like they do in road movies. But we were driving all the way from Princeton to my friend Chip's cabin in California. By the time we got to South Dakota, we were all out of stories and jokes.

Hey, look! It's

ω^{ω ω} = ω^ω2

That was cool. Then comes

ω^ω3, ... ω^ω4, ... ω^ω5, ...

and so on.

Anyway, back to my story. For the first half of our half of our trip across the state, we kept seeing signs for something called the South Dakota Tractor Museum.

Oh, wait, here's an interesting ordinal - let's slow down and take a look:

ω^ωω

I like that! Okay, let's keep driving:

ω^ωω + 1, ω^ωω + 2, ...

and then

ω^ωω + ω, ..., ω^ωω + ω 2, ..., ω^ωω + 3, ...

and then

ω^ωω + ω², ..., ω^ωω + ω³, ...

and eventually

ω^ωω + ω^ω

and eventually

ω^ωω + ω^ωω = ω^ωω 2

and then

ω^ωω 3, ..., ω^ωω 4, ..., ω^ωω 5, ...

and eventually

ω^ωω ω = ω^{ωω + 1}

and then

ω^{ωω + 2}, ..., ω^{ωω + 3}, ..., ω^{ωω + 4}, ...

This is pretty boring; we're already going infinitely fast, but we're still just picking up speed, and it'll take a while before we reach something interesting.

Anyway, we started getting really curious about this South Dakota Tractor Museum - it sounded sort of funny. It took 250 kilometers of driving before we passed it. We wouldn't normally care about a tractor museum, but there was really nothing else to think about while we were driving. The only thing to see were fields of grain, and these signs, which kept building up the suspense, saying things like "ONLY 100 MILES TO THE SOUTH DAKOTA TRACTOR MUSEUM!"

We're zipping along really fast now:

ω^ωωω, ..., ω^ωωωω,... , ω^ωωωωω,...

What comes after all these?

At this point we need to stop for gas. Our notation for ordinals runs out at this point!

The ordinals don't stop; it's just our notation that gives out. The set of all ordinals listed up to now - including all the ones we zipped past - is a well-ordered set called

ε₀

or "epsilon-nought". This has the amazing property that

ε₀ = ω^ε₀

And, it's the smallest ordinal with this property.

In fact, all the ordinals smaller than ε₀ can be drawn as trees. You write them in "Cantor normal form" like this:

ω^ωωω+ω+1 + ω^ωω+ωω + ω^ω + ω + ω + 1 + 1 + 1

using just + and exponentials and 1 and ω, and then you turn this notation into a picture of a tree. I'll leave it as a puzzle to figure out how.

So, the set of (finite, rooted) trees becomes a well-ordered set whose ordinal is ε₀. Trees are important in combinatorics and computer science, so ε₀ is not really so weird after all.

Another cool thing is that Gentzen proved the consistency of the usual axioms for arithmetic - "Peano arithmetic" - with the help of ε₀. He did this by drawing proofs as trees, and using this to give an inductive argument that there's no proof in Peano arithmetic that 0 = 1. But, this inductive argument goes beyond the simple kind you use to prove facts about all natural numbers. It uses induction up to ε₀.

You can't formalize Gentzen's argument in Peano arithmetic: thanks to Gödel, this system can't proof itself consistent unless it's not. I used to think this made Gentzen's proof pointless, especially since "induction up to ε₀" sounded like some sort of insane logician's extrapolation of ordinary mathematical induction.

But now I see that induction up to ε₀ can be thought of as induction on trees, and it seems like an obviously correct principle. Of course Peano's axioms also seem obviously correct, so I don't know that Gentzen's proof makes me more sure Peano arithmetic is consistent. But, it's interesting.

Induction up to ε₀ also lets you prove other stuff you can't prove with just Peano arithmetic. For example, it lets you prove that every Goodstein sequence eventually reaches zero!

Huh?

To write down a Goodstein sequence, you start with any natural number and write it in "recursive base 2", like this:

2²²⁺¹ + 2¹

Then you replace all the 2's by 3's:

3³³⁺¹ + 3¹

Then you subtract 1 and write the answer in "recursive base 3":

3³³⁺¹ + 1 + 1

Then you replace all the 3's by 4's, subtract 1 and write the answer in recursive base 4. Then you replace all the 4's by 5's, subtract 1 and write the answer in recursive base 5. And so on.

You can try some examples using the applet on this site:

1) National Curve Bank, Goodstein's theorem, http://curvebank.calstatela.edu/goodstein/goodstein.htm

You'll see that for any starting number bigger than 3, the Goodstein sequence seems to keep growing forever. So, it's shocking to learn that they all eventually go to zero!

For example, if you start with the number 4, you get this sequence:

4, 26, 41, 60, 83, 109, 139, 173, 211, 253, 299, 348, ...

Believe it or not, this goes to zero after about 7 × 10^121210694 steps! For a proof, see Kevin Buzzard's calculations in the Addendum at the bottom of this article.

In fact, it takes nothing but algebra, careful reasoning and persistence to work out when any given Goodstein sequence reaches zero. But, proving they all eventually reach zero uses induction up to ε₀.

How can that be?

The point is that these numbers in "recursive base n" look a lot like ordinals in Cantor normal form. If we translate them into ordinals by replacing n by ω, the ordinals keep getting smaller at each step, even when the numbers get bigger!

For example, when we do the translation

222+1 + 21       →    ωωω+1 + ω1
333+1 + 1 + 1    →    ωωω+1 + 1 + 1

we see the ordinal got smaller even though the number got bigger. Since ε₀ is well-ordered, the ordinals must bottom out at zero after a finite number of steps - that's what "induction up to ε₀" tells us. So, the numbers must too!

In short, induction up to ε₀ lets us prove all Goodstein sequences eventually reach zero. But Kirby and Paris showed something much deeper: they showed that you need induction up to ε₀ to get the job done.

And, they noted a big consequence of this fact. Suppose Peano arithmetic is consistent. Then you can't do induction up to ε₀ in this system - since if you could, Gentzen's work would let this system prove itself consistent, and Gödel's theorem would kick in and say it's not. But since you need induction up to ε₀ to prove all Goodstein sequences go to zero, you can't prove this in Peano arithmetic.

So, the fact that Goodstein sequences go to zero is obvious if you think about it the right way, but it's not provable in Peano arithmetic.

I don't know any results in mathematical physics that use induction up to ε₀, but these could be one - after all, trees show up in the theory of Feynman diagrams. That would be pretty interesting.

There's a lot more to say about this, but I hear what you're asking: what comes after ε₀?

Well, duh! It's

ε₀ + 1

Then comes

ε₀ + 2

and then eventually we get to

ε₀ + ω

and then

ε₀ + ω²,..., ε₀ + ω³,... ε₀ + ω⁴,...

and after a long time

ε₀ + ε₀ = ε₀ 2

and then eventually

ε₀²

and then eventually...

Oh, I see! You want to know the first really interesting ordinal after ε₀.

Well, this is a matter of taste, but you might be interested in ε₁. This is the first ordinal after ε₀ that satisfies this equation:

x = ω^x

How do we actually reach this ordinal? Well, just as ε₀ was the limit of this sequence:

ω, ω^ω, ω^ωω, ω^ωωω,...

ε₁ is the limit of this:

ε₀ + 1, ω^{ε₀ + 1}, ω^{ωε₀ + 1}, ω^{ωωε₀ + 1},...

In other words, it's the union of all these well-ordered sets.

In what sense is ε₁ the "first really interesting ordinal" after ε₀? I'm not sure! Maybe it's the first one that can't be built out of 1, ω and ε₀ using finitely many additions, multiplications and exponentiations. Does anyone out there know?

Anyway, the next really interesting ordinal I know after ε₁ is ε₂. It's the next solution of

x = ω^x

and it's defined to be the limit of this sequence:

ε₁ + 1, ω^{ε₁ + 1}, ω^{ωε₁ + 1}, ω^{ωωε₁ + 1},...

Maybe now you get the pattern. In general, ε_α is the αth solution of

x = ω^x

and we can define this, if we're smart, for any ordinal α.

So, we can keep driving on through fields of ever larger ordinals:

ε₂,..., ε₃,..., ε₄, ...

and eventually

ε_ω,..., ε_ω+1,..., ε_ω+2,...

and eventually

ε_ω²,... , ε_ω³,..., ε_ω⁴,...

and eventually

ε_ω^ω,..., ε_ω^ωω,...

As you can see, this gets boring after a while - it's suspiciously similar to the beginning of our trip through the ordinals, with them now showing up as subscripts under this "ε" notation. But this is misleading: we're moving much faster now. I'm skipping over much bigger gaps, not bothering to mention all sorts of ordinals like

ε_ω^ω + ε_{ω 248} + ω^{ωω + 17} + 1

Anyway... so finally we got to this South Dakota Tractor Museum, driving pretty darn fast at this point, about 85 miles an hour... and guess what?

Oh - wait a minute - it's sort of interesting here:

ε_ε0,..., ε_ε1,..., ε_ε2,...

and now we reach

ε_εω

and then

ε_εω^ω,..., ε_εω^ωω,...

and then as we keep speeding up, we see:

ε_εε0,... ε_εεε0,... ε_εεεε0,...

So, anyway: by the time we got that tractor museum, we were driving really fast. And, all we saw as we whizzed by was a bunch of rusty tractors out in a field! It was over in a split second! It was a real anticlimax - just like this little anecdote, in fact.

But that's the way it is when you're driving through these ordinals. Every ordinal, no matter how large, looks pretty pathetic and small compared to the ones ahead - so you keep speeding up, looking for a really big one... and when you find one, you see it's part of a new pattern, and that gets boring too...

Anyway, when we reach the limit of this sequence:

ε₀, ε_ε0, ε_εε0, ε_εεε0, ε_εεεε0,...

our notation breaks down, since this is the first solution of

x = ε_x

We could make up a new name for this ordinal, like η₀.

Then we could play the whole game again, defining η_α to be the αth solution of

x = ε_x

sort of like how we defined the epsilons. This kind of equation, where something equals some function of itself, is called a "fixed point" equation.

But since we'll have to play this game infinitely often, we might as well be more systematic about it!

As you can see, we keep running into new, qualitatively different types of ordinals. First we ran into the powers of ω, then we ran into the epsilons, and now these etas. It's gonna keep happening! For each type of ordinal, our notation runs out when we reach the first "fixed point" - when the xth ordinal of this type is actually equal to x.

So, instead of making up infinitely many Greek letters, let's use φ_γ for the γth type of ordinal, and φ_γ(α) for the αth ordinal of type γ.

We can use the fixed point equation to define φ_γ+1 in terms of φ_γ. In other words, we start off by defining

φ₀(α) = ω^α

and then define

φ_γ+1(α)

to be the αth solution of

x = φ_γ(x)

We can even define this stuff when γ itself is infinite. For a more precise definition see the Wikipedia article cited below... but I hope you get the rough idea.

This defines a lot of really big ordinals, called the "Veblen hierarchy".

There's a souped-up version of Cantor normal form that can handle every ordinal that's a finite sum of guys in the Veblen hierarchy: you can write them uniquely as finite sums of the form

φ_γ1(α₁) + ... + φ_γk(α_k)

where each term is less than or equal to the previous one, and each α_i is not a fixed point of φ_γi

But as you might have suspected, not all ordinals can be written in this way. For one thing, every ordinal we've reached so far is countable: as a set you can put it in one-to-one correspondence with the integers. There are much bigger uncountable ordinals - at least if you believe you can well-order uncountable sets.

But even in the realm of the countable, we're nowhere near done!

As I hope you see, the power of the human mind to see a pattern and formalize it gives the quest for large countable ordinals a strange quality. As soon as we see a systematic way to generate a sequence of larger and larger ordinals, we know this sequence has a limit that's larger then all of those! And this opens the door to even larger ones....

So, this whole journey feels a bit like trying to outrace our car's own shadow - the faster we drive, the faster it chases after us. But, it's interesting to hear what happens next. At this point we reach something a bit like the Badlands on the western edge of South Dakota - something a bit spooky!

It's called the Feferman-Schütte ordinal, Γ₀. This is just the limit, or union if you prefer, of all the ordinals mentioned so far: all the ones you can get from the Veblen hierarchy. You can also define Γ₀ by a fixed point property: it's the smallest ordinal x with

φ_x(0) = x

Now, we've already seen that induction up to different ordinals gives us different amounts of mathematical power: induction up to ω is just ordinary mathematical induction as formalized by Peano arithmetic, but induction up to ε₀ buys us more - it lets us prove the consistency of Peano arithmetic!

Logicians including Feferman and Schütte have carried out a detailed analysis of this subject. They know a lot about how much induction up to different ordinals buys you. And apparently, induction up to Γ₀ lets us prove the consistency of a system called "predicative analysis". I don't understand this, nor do I understand the claim I've seen that Γ₀ is the first ordinal that cannot be defined predicatively - i.e., can't be defined without reference to itself. Sure, saying Γ₀ is the first solution of

φ_x(0) = x

is non-predicative. But what about saying that Γ₀ is the union of all ordinals in the Veblen hierarchy? What's non-predicative about that?

If anyone could explain this in simple terms, I'd be much obliged.

As you can see, I'm getting out my depth here. That's pretty typical in This Week's Finds, but this time - just to shock the world - I'll take it as a cue to shut up. So, I won't try to explain the outrageously large Bachmann-Howard ordinal, or the even more outrageously large Church-Kleene ordinal - the first one that can't be written down using any computable system of notation. You'll just have to read the references.

For a fun introduction to the infinite, try

2) Rudy Rucker, Infinity and the Mind: The Science and Philosophy of the Infinite, Princeton University Press, Princeton, 2004.

Rucker also wrote a novel, White Light, about a mathematician who actually goes to the transfinite realms and climbs some transfinite mountains.

For online self-study, I urge you to start by reading the Wikipedia article on ordinal numbers, then the article on ordinal arithmetic, and then the one on large countable ordinals - they're really well-written:

3) Wikipedia, Ordinal numbers, http://en.wikipedia.org/wiki/Ordinal_number

Ordinal arithmetic, http://en.wikipedia.org/wiki/Ordinal_arithmetic

Large countable ordinals, http://en.wikipedia.org/wiki/Large_countable_ordinals

The last one has a tempting bibliography, but warns us that most books on this subject are hard to read and out of print. Apparently nobody can agree on notation for ordinals beyond the Veblen hierarchy, either.

Gentzen proved the consistency of Peano arithmetic in 1936:

4) Gerhard Gentzen, Die Widerspruchfreiheit der reinen Zahlentheorie, Mathematische Annalen 112 (1936), 493-565. Translated as "The consistency of arithmetic" in M. E. Szabo ed., The Collected Works of Gerhard Gentzen, North-Holland, Amsterdam, 1969.

Goodstein's theorem came shortly afterwards:

5) R. Goodstein, On the restricted ordinal theorem, Journal of Symbolic Logic, 9 (1944), 33-41.

but Kirby and Paris proved it independent of Peano arithmetic only in 1982:

6) L. Kirby and J. Paris, Accessible independence results for Peano arithmetic, Bull. London. Math. Soc. 14 (1982), 285-93.

That marvelous guy Alan Turing wrote his PhD thesis at Princeton under the logician Alonzo Church. It was about ordinals and their relation to logic:

7) Alan M. Turing, Systems of logic defined by ordinals, Proc. London Math. Soc., Series 2, 45 (1939), 161-228.

This is regarded as his most difficult paper. The idea is to take a system of logic like Peano arithmetic and throw in an extra axiom saying that system is consistent, and then another axiom saying that system is consistent, and so on ad infinitum - getting a new system for each ordinal. These systems are recursively axiomatizable up to (but not including) the Church-Kleene ordinal.

These ideas were later developed much further....

But, reading original articles is not so easy, especially if you're in Shanghai without access to a library. So, what about online stuff - especially stuff for the amateur, like me?

Well, this article is great fun if you're looking for a readable overview of the grand early days of proof theory, when Hilbert was battling Brouwer, and then Gödel came and blew everyone away:

8) Jeremy Avigad and Erich H. Reck, "Clarifying the nature of the infinite": the development of metamathematics and proof theory, Carnegie-Mellon Technical Report CMU-PHIL-120, 2001. Also available as http://www.andrew.cmu.edu/user/avigad/Papers/infinite.pdf

But, it doesn't say much about the newer stuff, like the idea that induction up to a given ordinal can prove the consistency of a logical system - the bigger the ordinal, the stronger the system. For work up to 1960, this is a good overview:

9) Solomon Feferman, Highlights in proof theory, in Proof Theory, eds. V. F. Hendricks et al, Kluwer, Dordrecht (2000), pp. 11-31. Also available at http://math.stanford.edu/~feferman/papers.html

For newer stuff, try this:

10) Solomon Feferman, Proof theory since 1960, prepared for the Encyclopedia of Philosophy Supplement, Macmillan Publishing Co., New York. Also available at http://math.stanford.edu/~feferman/papers.html

Also try the stuff on proof theory, trees and categories mentioned in "week227", and this book mentioned in "week70" - now you can get it free online:

11) Jean-Yves Girard, Y. Lafont and P. Taylor, Proofs and Types, Cambridge Tracts in Theoretical Computer Science 7, Cambridge U. Press, 1989. Also available at http://www.cs.man.ac.uk/~pt/stable/Proofs+Types.html

Finally, sometime I want to get ahold of this book by someone who always enlivened logic discussions on the internet until his death in April this year:

12) Torkel Franzen, Inexhaustibility: A Non-Exhaustive Treatment, Lecture Notes in Logic 16, A. K. Peters, Ltd., 2004.

The blurb sounds nice: "The inexhaustibility of mathematical knowledge is treated based on the concept of transfinite progressions of theories as conceived by Turing and Feferman."

Okay, now for a bit about the icosahedron - my favorite Platonic solid.

I've been thinking about the "geometric McKay correspondence" lately, and among other things this sets up a nice relationship between the symmetry group of the icosahedron and an amazing entity called E₈. E₈ is the largest of the exceptional Lie groups - it's 248-dimensional. It's related to the octonions (the number "8" is no coincidence) and it shows up in string theory. It's very beautiful how this complicated sounding stuff can be seen in distilled form in the icosahedron.

I have a lot to say about this, but you're probably worn out by our road trip through the land of big ordinals. So for now, try "week164" and "week230" if you're curious. Let's talk about something less stressful - the early history of the icosahedron.

I spoke about the early history of the dodecahedron in "week63". It's conjectured that the Greeks got interested in this shape from looking at crystals of iron pyrite. These aren't regular dodecahedra, since normal crystals can't have 5-fold symmetry - though "quasicrystals" can. Instead, they're "pyritohedra". The Greeks' love of mathematical perfection led them to the regular dodecahedron....

... and it also led them to invent the icosahedron:

13) Benno Artmann, About the cover: the mathematical conquest of the third dimension, Bulletin of the AMS, 43 (2006), 231-235. Also available at http://www.ams.org/bull/2006-43-02/S0273-0979-06-01111-6/

According to Artmann, an ancient note written in the margins of a copy of Euclid's Elements says the regular icosahedron and octahedron were discovered by Theaetetus!

If you're a cultured sort, you may know Theaetetus through Plato's dialog of the same name, where he's described as a mathematical genius. He's also mentioned in Plato's "The Sophist". He probably discovered the icosahedron between 380 and 370 BC, and died at an early age in 369. Euclid wrote his construction of the icosahedron that we find in Euclid's Elements:

14) Euclid, Elements, Book XIII, Proposition 16, online version due to David Joyce at http://aleph0.clarku.edu/~djoyce/java/elements/bookXIII/propXIII16.html

Artmann says this was the first time a geometrical entity appeared in pure thought before it was seen! An interesting thought.

Book XIII also contains a complete classification of the Platonic solids - perhaps the first really interesting classification theorem in mathematics, and certainly the first "ADE classification":

15) Euclid, Elements, Book XIII, Proposition 18, online version due to David Joyce at http://aleph0.clarku.edu/~djoyce/java/elements/bookXIII/propXIII18.html

If you don't know about ADE classifications, see "week62".

I got curious about the "ancient note written in the margins of a copy of Euclid" that Artmann mentions. It seemed too good to be true. Just for fun, I tried to track down the facts about this, using only my web browser here in Shanghai.

First of all, if you're imagining an old book in a library somewhere with marginal notes scribbled by a pal of Theaetetus, dream on. It ain't that simple! Our knowledge of Euclid's original Elements relies on copies of copies of copies... and centuries of detective work, with each detective having to root through obscure journals and dim-lit library basements to learn what the previous detectives did.

The oldest traces of Euclid's Elements are pathetic fragments of papyrus. People found some in a library roasted by the eruption of Mount Vesuvius in 79 AD, some more in a garbage dump in the Egyptian town of Oxyrhynchus (see "week221"), and a couple more in the Fayum region near the Nile. All these were written centuries after Euclid died. Here's one from Oxyrhynchus, photographed by Bill Casselman, who kindly let me include this picture:

What math is being discussed here? What's that red "29" doing there? For the answer to these and other questions, check out his website!

16) Bill Casselman, One of the oldest extant diagrams from Euclid, http://www.math.ubc.ca/~cass/Euclid/papyrus/

The oldest nearly complete copy of the Elements lurks in a museum called the Bodleian at Oxford. It dates back to 888 AD, about a millennium after Euclid.

More copies date back to the 10th century; you can find their stories here:

17) Thomas L. Heath, editor, Euclid's Elements, chap. V: the text, Cambridge U. Press, Cambridge, 1925. Also available at http://www.perseus.tufts.edu/cgi-bin/ptext?lookup=Euc.+5

18) Menso Folkerts, Euclid's Elements in Medieval Europe, http://www.math.ubc.ca/~cass/Euclid/folkerts/folkerts.html

All these copies are somewhat different. So, getting at Euclid's original Elements is as hard as sequencing the genome of Neanderthal man, seeing a quark, or peering back to the Big Bang!

A lot of these copies contain "scholia": comments inserted by various usually unnamed copyists. These were collected and classified by a scholar named Heiberg in the late 1800s:

19) Thomas L. Heath, editor, Euclid's Elements, chap. VI: the scholia, Cambridge U. Press, Cambridge, 1925. Also available at http://www.perseus.tufts.edu/cgi-bin/ptext?lookup=Euc.+6

One or more copies contains a scholium about Platonic solids in book XIII. Which copies? Ah, for that I'll have to read Heiberg's book when I get back to UC Riverside - our library has it, I'm proud to say.

And, it turns out that another scholar named Hultsch argued that this scholium was written by Geminus of Rhodes.

Geminus of Rhodes was an astronomer and mathematician who may have lived between 130 and 60 BC. He seems like a cool dude. In his Introduction to Astronomy, he broke open the "celestial sphere", writing:

... we must not suppose that all the stars lie on one surface, but rather that some of them are higher and some are lower.

Anyway, the first scholium in book XIII of Euclid's Elements, which Hultsch attributes to Geminus, mentions

... the five so-called Platonic figures which, however, do not belong to Plato, three of the five being due to the Pythagoreans, namely the cube, the pyramid, and the dodecahedron, while the octahedron and the icosahedron are due to Theaetetus.

20) Benno Artmann, Antike Darstellungen des Ikosaeders, Mitt. DMV 13 (2005), 45-50. (Here the drawing of the icosahedron in Euclid's elements is analysed in detail.)

21) A. E. Taylor, Plato: the Man and His Work, Dover Books, New York, 2001, page 322. (This discusses traditions concerning Theaetetus and Platonic solids.)

22) Euclid, Elementa: Libri XI-XIII cum appendicibus, postscript by Johan Ludvig Heiberg, edited by Euangelos S. Stamatis, Teubner BSB, Leipzig, 1969. (Apparently this contains information on the scholium in book XIII of the Elements.)

Now for something a bit newer: categorification and quantum mechanics. I've said so much about this already that I'm pretty much talked out:

23) John Baez and James Dolan, From finite sets to Feynman diagrams, in Mathematics Unlimited - 2001 and Beyond, vol. 1, eds. Björn Engquist and Wilfried Schmid, Springer, Berlin, 2001, pp. 29-50.

24) John Baez and Derek Wise, Quantization and Categorification, Quantum Gravity Seminar lecture notes, available at: http://math.ucr.edu/home/baez/qg-fall2003/ http://math.ucr.edu/home/baez/qg-winter2004/ http://math.ucr.edu/home/baez/qg-spring2004/

As I explained in "week185", many basic facts about harmonic oscillators, Fock space and Feynman diagrams have combinatorial interpretations. For example, the commutation relation between the annihilation operator a and the creation operator a*:

aa* - a*a = 1

comes from the fact that if you have some balls in a box, there's one more way to put a ball in and then take one out than to take one out and then put one in! This way of thinking amounts to using finite sets as a substitute for the usual eigenstates of the number operator, so we're really "categorifying" the harmonic oscillator: giving it a category of states instead of a set of states.

Working out the detailed consequences takes us through Joyal's theory of "structure types" or "species" - see "week202" - and on to more general "stuff types". Some nice category and 2-category theory is needed to make the ideas precise. For a careful treatment, see this thesis by a student of Ross Street:

25) Simon Byrne, On Groupoids and Stuff, honors thesis, Macquarie University, 2005, available at http://www.maths.mq.edu.au/~street/ByrneHons.pdf and http://math.ucr.edu/home/baez/qg-spring2004/ByrneHons.pdf

However, none of this work dealt with the all-important phases in quantum mechanics! For that, we'd need a generalization of finite sets whose cardinality can be be complex. And that's what my student Jeffrey Morton introduces here:

26) Jeffrey Morton, Categorified algebra and quantum mechanics, Theory and Application of Categories 16 (2006), 785-854. Available at http://www.emis.de/journals/TAC/volumes/16/29/16-29abs.html; also available as math.QA/0601458.

He starts from the beginning, explains how and why one would try to categorify the harmonic oscillator, introduces the "U(1)-sets" and "U(1)-stuff types" needed to do this, and shows how the usual theorem expressing time evolution of a perturbed oscillator as a sum over Feynman diagrams can be categorified. His paper is now the place to read about this subject. Take a look!

Jeffrey Winkler wrote:

Are the ridiculously infinite forms of infinity you discuss in your article ever used for anything?

If they only refer to themselves, if the only thing these infinite sets refer to is other infinite sets, then it's pointless self-reflexive recursive circular reasoning. A set that has the same number of elements as the number of apples on your table, or the number of points in a line or a plane, or in infinitely dimensional Hilbert space, could be said to refer to something, but give an example of something, other than one of the sets you're talking about, which would have ε₀ elements. Where in mathematics or physics would you ever use such a concept? If you never would, then what's the point? In other words, is there anything where you could have ε₀ "many" of something, other than the sets themselves, and if there isn't, then are these actually numbers? If nothing is ever "that many", then is it a number? Of course, we've expanded the concept of "number" to include complex numbers, quaternions, octonions, vectors, tensors, matrices, etc. where they don't literally correspond to "how many" something is, yet in all those examples, they have uses in various fields of mathematics and physics, other than just when talking about themselves, so there is a reason for inventing them.

Jeffery

Jeffery Winkler wrote:

 > Are the ridiculously infinite forms of infinity you discuss 
 > in your article ever used for anything?

Without ε₀ you can't prove that Goodstein sequences converge to zero - an obviously true fact. As I mentioned, the main use of these ordinals is to measure the strength of axiom systems. But, I didn't write about these ordinals because they're useful. I wrote about them because they're fun.

They're not "ridiculously infinite", though. The ordinals I mentioned are all countable ordered sets, and you can describe them all explicitly as subsets of the rational numbers.

More precisely: any one of the ordinals I mentioned, up to and including the Feferman-Schütte ordinal (and quite a ways beyond), is isomorphic as an ordered set to a subset of the rational numbers. Moreover, you can write a computer program that will decide whether or not any given fraction is in this subset. As a consequence, you can also write a computer program that lists the fractions in this set.

It's pretty obvious how to do this for ω²:

But you can do it for any one of the ordinals I mentioned! David Madore has drawn a picture of ε₀, for example.

So, for someone to reject these ordinals as "ridiculously infinite", they must have some doubts about the legitimacy of computable subsets of the rational numbers as valid objects of study. That seems like an extreme position.

The Church-Kleene ordinal is much larger than any of the ordinals I discussed in detail. It's still countable. Any ordinal below it can be described in a computable way - but it itself can't. So, if you believe that only computable mathematical entities are worth studying, you might want to stop shy of this one. I stopped far short of this one.

 > If they only refer to themselves, if the only thing these 
 > infinite sets refer to is other infinite sets, then it's 
 > pointless self-reflexive recursive circular reasoning. 

I hope you see that this is not true for the countable ordinals I was discussing. I deliberately refrained from mentioning the large cardinals that logicians often discuss, precisely because I share your distaste for such stuff.

I realized after I posted "week236" that some people might think I was talking about mystical entities, when I was actually talking about very concrete things. So, I'm glad you brought this up.

Best,
jb

And now for Kevin Buzzard's wonderful calculation! In the original version of this Week's Finds, I wrote:

if you start with the number 4, you get this Goodstein sequence:

4, 26, 41, 60, 83, 109, 139, 173, 211, 253, 299, 348, ...

and apparently it takes about 3 × 10^60605351 steps to reach zero!

Kevin Buzzard then sent me an email in which he worked out the number himself. After correcting a few small mistakes, we seem to have settled on a different answer.

Kevin writes:

 You write this as if it were some kind of mystery. I remember working
 out this number explicitly when I was a graduate student!  There is
 some nice form for it, as I recall.  Let's see if I can reconstruct
 what I did.

 If I've understood the sequence correctly, it should be (where "n)" 
 at the beginning of a line denotes we're working in base n on this 
 line, so strictly speaking it's probably the n-1st term in the sequence)
 
 2) 2^2 = 4
 3) 3^3-1 = 2.3^2+2.3+2 = 26 [note: base 3, ends in 2, and 3+2=5]
 4) 2.4^2+2.4+1 = 41 [note: base 4, ends in 1, and 4+1=5]
 5) 2.5^2+2.5 = 60 [we're at a limit ordinal here, note 3+2=4+1=5]
 6) 2.6^2+2.6-1 = 2.6^2+6+5 = 83 [note: base 6, ends in 5]
 7) 2.7^2+7+4 [note: base 7, ends in 4]
 8) 2.8^2+8+3 [note: base 8, ends in 3, so we next get a limit ordinal at...]
 .
 .
 11) 2.11^2+11
 12) 2.12^2+12-1 = 2.12^2+11
 13) 2.13^2+10
 .
 .
 .
 23) 2.23^2 (as 23 = 12+11 = 13+10= ...)
 24) 24^2+23.24+23
 .
 .
 .
 47) 47^2+23.47
 48) 48^2+22.48+47
 .
 .
 .
 95) 95^2+22.95
 96) 96^2+21.96+95
 .
 .
 .
 
 and now we spot a pattern: we're just doubling---getting a limit ordinal
 at bases 24-1, 48-1, 96-1 and so on. Let's look again at those limit
 ordinals:
 
 47) 47^2+23.47
 95) 95^2+22.95
 .
 .
 .
 24*2^t-1) (24*2^t-1)^2+(24-t)*(24*2^t-1)
 .
 .
 .
 
 so the last one with a square in it will be the case t=24, corresponding 
 to
 
 r) r^2
 
 where 
 
 r = 24 * 2^24 - 1 = 402653183. 
 
 All those 24s, but I'm sure you'll not get carried away.  Let's define 

 n = r+1 = 24 * 2^24 

 and continue on. At the next step, the ordinal decreases sharply:

 n)      n^2-1 = (n-1)n + (n-1)
 n+1)   (n-1)(n+1) + (n-2) [note: now back to the usual tricks]
 .
 .
 .
 2n-1) (n-1)(2n-1)        [the next limit, at base 2n-1]
 2n)   (n-2)(2n) + (2n-1)
 .
 .
 .
 4n-1) (n-2)(4n-1)
 4n)   (n-2)(4n)+(4n-1)
 .
 .
 .
 
 and the limit ordinals we're running into now (and we're going to
 run into about n of them, which is a lot), are
 
 2n-1)      (n-1)(2n-1)
 4n-1)      (n-2)(4n-1)
 8n-1)      (n-3)(8n-1)
 .
 .
 .
 n2^s-1)    (n-s)(n2^s - 1)
 .
 .
 .
 
 and finally when s = n-1
 
 m)           m
 
 where m = n 2^{n-1} - 1.  The sequence now looks like
 
 m+1) (m+1)-1 = m  
 m+2)  m-1        
 m+3)  m-2
 .
 .
 .
 2m+1) 0
 
 So the sequence becomes zero at base n2^n - 1, where n = 24 * 2^24.
 If 2^2 is the first term in the sequence, I guess this is
 the (n2^n - 2)th term.  I make this about 6.9*10^{121210694} -
 curses, you got something else!  Actually, I have about the square
 of what you wrote and hence I have most likely made a slip.  On the 
 other hand you can see that it's not a mystery at all, it's just an
 elementary exercise.  It really helps you learn about why the 
 countable ordinals are well-ordered too: as you continue working
 out the numbers, you always have this impending sense of doom 
 telling you that your gut feeling that the sequence tends to 
 infinity might just be wrong...

 Kevin

n = 24 · 2²⁴ = 402653184.

By the (2n)th term it reaches almost 2n².

Then it grows by steps of n-2, and by the (4n)th term it reaches almost 4n².

Then it grows by steps of n-3, and by the (8n)th term it reaches almost 8n².

And so on... it's slowing down now.

After about the (2^n-2n)th term it levels off completely, and by the (2^n-1n)th term it equals almost 2^n-1n. Note these numbers are the same.

From this point on the sequence decreases by one each time, and it hits zero at about the (2ⁿ n)th term.

So, it spends the last half of its life decreasing by one each time. Right before that, it spends a quarter of its life remaining constant. Right before that, it spends an eighth of its life growing by one each time. Right before that it, it spends a sixteenth of its life growning by two each time. And so on, but not indefinitely: this description covers the phase after the nth term.

In particular, it reaches its maximum and then levels off after about quarter of its life is done. It spends about the next quarter of its life being constant, and the next half going down one step at a time.

Let's be a bit more precise. For this let's call the ith term of the 4th Goodstein sequence a_i, where we count things so that

a1 = 4, a2 = 26, ...

Then a_i first reaches its maximum value at exactly

i = (1/4) 24 224 2(24 224) - 2 

  ~  1.72 × 10121210694

Its value at this point is exactly

ai = (1/2) 24 224 2(24 224) - 1

  ~  3.45 × 10121210694

i = 24 224 2(24 224) - 2
  
  ~ 6.89 × 10121210694

I was worried that Kevin and I had made a mistake until we found this thesis which gets the same answer (though the author starts the sequence at a₀ = 4, so it looks one off from ours):

27) Justin T. Miller, On the Independence of Goodstein's Theorem, Masters thesis, University of Arizona, 2001. Also available as http://www.u.arizona.edu/~miller/thesis/thesis.html

Tim Chow had some comments about why the Feferman-Schütte ordinal is considered the first "impredicative" ordinal. He wrote:

John Baez wrote:

 >Logicians including Feferman and Schütte have carried out a detailed 
 >analysis of this subject.  They know a lot about how much induction 
 >up to different ordinals buys you.  And apparently, induction up to 
 >Γ0 lets us prove the consistency of a system called "predicative
 >analysis".  I don't understand this, nor do I understand the claim
 >I've seen that Γ0 is the first ordinal that cannot be defined
 >predicatively - i.e., can't be defined without reference to itself.  
 >Sure, saying Γ0 is the first solution of
 >
 >φx(0) = x
 >
 >is non-predicative.  But what about saying that Γ0 is the union 
 >of all ordinals in the Veblen hierarchy?  What's non-predicative
 >about that?

The situation is somewhat akin to the situation with the Church-Turing thesis, in that one is tentatively equating an informal notion (predicativity or computability) with a precise mathematical notion. Therefore there is no definitive answer to your question, and Feferman himself has articulated potential objections to the "standard view" that Γ₀ marks the boundary of predicativity.

Having said that, I'll also say that one of the reasons for the standard view is that Γ₀ marks the boundary of "autonomous progressions" of arithmetical theories. The book by Torkel Franzen that you cited is probably the most accessible introduction to this subject. Roughly speaking, the idea is that if anyone fully accepts first-order Peano arithmetic PA, then implicitly he accepts its consistency Con(PA), as well as Con(PA+Con(PA)), etc. If one tries to articulate exactly what is "implicitly" involved in accepting PA in this sense, then one can make a plausibility argument that Γ₀ is a natural stopping point. I think you have a better shot at grasping the underlying intuition via this approach than by staring at Γ₀ itself and trying to figure out what is non-predicative about its definition.

There's also someone named Nik Weaver who has debated Feferman on this subject:

http://www.cs.nyu.edu/pipermail/fom/2006-April/010472.html
http://www.math.wustl.edu/~nweaver/conceptualism.html

He seems to claim that Γ₀ and even larger ordinals have predicative definitions. However, I'm too ignorant to follow this debate. Usually in physics I have a sense for when people are being reasonable even if I don't follow the details. In this debate I can't even do that.

Let's look more closely at what the notion of "one theory like this per ordinal" means. There's no difficulty figuring out what "Con(PA)" means or how to express that statement in the first-order language of arithmetic. Ditto with "Con(PA+Con(PA))". However, once you start ascending the ordinal hierarchy, a difficulty appears. The language of arithmetic doesn't let you talk about "ordinals" directly---that's a set-theoretical concept. In order to express a statement like "Con(T)" for some theory T, you need at minimum to be able to give some sort of "recursive description" or "recursive axiomatization" of T (where here I use the word "recursive" in the technical sense of recursive function theory) in the first-order language of arithmetic. This observation already yields the intuition that we're not going to be able to ascend beyond the Church-Kleene ordinal, because we won't even be able to figure out how to say "T is consistent" for a theory T that requires that many iterations to reach from PA.

There are other problems, though, that potentially get in the way before we reach the Church-Kleene ordinal. Once we realize that what we need is a system of "ordinal notations" to "fake" the relevant set theory, we may (if we are predicativists) worry about issues such as:

1. As we ascend the ordinal hierarchy, isn't it illegitimate to make a jump to an ordinal α unless we've already proved, at the level of some ordinal β that we've already reached, that an ordinal of type α exists?

2. And isn't it illegitimate to create sets by quantification over things other than the natural numbers themselves and sets that we've already created?

Condition 1 goes by the name of "autonomy" and condition 2 goes by the name of "ramification." If one formalizes these notions in a certain plausible manner, then one arrives at Γ₀ as the least upper bound of theories that you can get to, starting with (for example) PA.

One can of course wonder whether 1 and 2 above really capture the concept of "predicativity." Some secondary evidence has accumulated of the following form: Some argument that intuitively seems to be predicative but that is not immediately seen to be provable in the Feferman-Schütte framework is shown, after some work, to indeed be provable below Γ₀.

It's still possible, of course, for someone---you mentioned Nik Weaver--- to come along and argue that our intuitive notion of predicativism, fuzzy though it is, can't possibly be identified with the level Γ₀. The reason you can't seem to decide immediately whether Weaver's position is nonsensical or not is probably because the critical questions are not mathematical but philosophical, and of course it's usually harder to arrive at definitive answers in philosophy than in mathematics.

28) Hilbert Levitz, Transfinite ordinals and their notations: For the uninitiated, available at http://www.cs.fsu.edu/~levitz/research.html

This paper introduced the "Schütte Klammersymbole", which generalize the Veblen hierarchy:

29) Kurt Schütte, Kennzeichnung von Orgnungszahlen durch rekursiv erklärte Funktionen, Math. Ann 127 (1954), 15-32.

These papers discuss a general concept of "ordinal notation system", which includes the Schütte Klammersymbole and also something called the "n-ary Veblen hierarchy":

30) Anton Setzer, An introduction to well-ordering proofs in Martin-Löf's type theory, in Twenty-Five Years of Constructive Type Theory, eds. G. Sambin and J. Smith, Clarendon Press, Oxford, 1998, pp. 245-263. Also available at http://www.cs.swan.ac.uk/~csetzer/index.html

Anton Setzer, Ordinal systems, in Sets and Proofs, Cambridge U. Press, Cambridge, 2011, pp. 301-331. Also available at http://www.cs.swan.ac.uk/~csetzer/index.html

This paper has a nice expository section on generalizations of the Veblen hierarchy:

31) Jean H. Gallier, What's so special about Kruskal's theorem and the ordinal Γ₀? A survey of some results in proof theory, sec. 7, A glimpse at Veblen hierarchies, Ann. Pure Appl. Logic 53 (1991), 199-260. Also available at http://www.cis.upenn.edu/~jean/gallier-old-pubs.html

This paper is very useful, since it compares different notations:

32) Larry W. Miller, Normal functions and constructive ordinal notations, J. Symb. Log. 41 (1976), 439-459.

You can get it through JSTOR if you have access to that.

This webpage gives a nice definition of "ordinal notation system" as a coalgebra of a certain functor - nice if you understand categories, that is:

33) Peter Hancock, Ordinal notation systems, http://homepages.inf.ed.ac.uk/v1phanc1/ordinal-notations.html

Kevin Watkins pointed out this website, which contains several papers on ordinal notations:

34) Harold Simmons, Abstracts of papers and notes, http://www.cs.man.ac.uk/~hsimmons/DOCUMENTS/papersandnotes.html

Finally, the Wikipedia article on "large countable ordinals" has some references to books which are, alas, out of print.

Then he almost fell flat on his face on the floor
When I picked up the chalk and drew one letter more!
A letter he never had dreamed of before!
And I said, "You can stop, if you want, with the Z
Because most people stop with the Z
But not me!
In the places I go there are things that I see
That I never could spell if I stopped with the Z.
I'm telling you this 'cause you're one of my friends.
My alphabet starts where your alphabet ends!" - Doctor Seuss

© 2006 John Baez
baez@math.removethis.ucr.andthis.edu