




|
 
|

|
After leaving the Perimeter Institute near the end of June, I went home to Riverside and then took off for a summer in Shanghai. That's where I am now. I'm having a great time - you can read about it in my online diary!
Today I'll talk about classical and quantum computation, then quantum gravity, and finally a bit about higher gauge theory.
My interest in quantum computation was revived when Scott Aaronson invited me to this building near the Perimeter Institute:
1) Institute for Quantum Computing (IQC), http://www.iqc.ca/
Raymond Laflamme gave me a fun tour of the labs, especially the setup where he's using nuclear magnetic resonance to control the spins of three carbon-13 nuclei in a substance called malonic acid. Each molecule is its own little quantum computer:
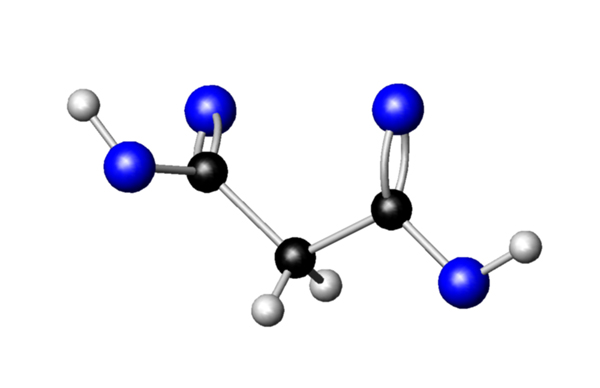
This picture was drawn by Osama Moussa, a grad student working with Laflamme on this project. The black spheres are carbons, the whites are hydrogens and the blues are oxygens.
One of the banes of quantum computation is "decoherence", in which the quantum state of the computer interacts with its environment and becomes correlated with it, or "entangled", in a way that appears to "collapse its wavefunction" and ruin the calculation.
In general it's good to keep things cool if you don't want things to get messed up. Surprisingly, Laflamme said that for liquids, keeping them hot reduces the rate of decoherence: the different molecules zip around so fast they don't stay near each other long enough to affect each other much!
But malonic acid is a solid, so the main way to keep the molecules from disturbing each other is to keep them far apart on average. So, they dilute the malonic acid made using carbon-13 nuclei in a lot of ordinary malonic acid made using carbon-12. Since 12 is an even number, such carbon atoms have no unpaired spinning neutron in their nuclei. So, the ordinary malonic acid serves as an inert "shield" that keeps the active molecules well separated most of the time.
So, each active molecule acts like an isolated system, doing its own computation as they zap it with carefully timed pulses of microwaves and the three spinning nuclei interact. About a quadrillion of these molecules are doing their thing in parallel, mixed in with a bunch more made using carbon-12. For more details, see:
2) Jonathan Baugh, Osama Moussa, Colm A. Ryan, Raymond Laflamme, Chandrasekhar Ramanathan, Timothy F. Havel and David G. Cory, Solid-state NMR three-qubit homonuclear system for quantum information processing: control and characterization, Phys. Rev. A 73 (2006), 022305. Also available as quant-ph/0510115.
Laflamme also showed me some beams of spin-entangled photons which they can use as keys for quantum cryptography. Nobody can peek at these photons without affecting them! It's a great scheme. If you don't know it, try this simple explanation:
3) Artur Ekert, Cracking codes, part II, Plus Magazine, http://pass.maths.org.uk/issue35/features/ekert/index.html
There are already two companies - idQuantique and MagiQ - selling quantum key distribution systems that send entangled photons down optical fibers. But the folks at the IQC are planning to send them right through the air!
Eventually they want to send them from satellites down to the Earth. But as a warmup, they'll send beams of entangled photons from an intermediate building to the Institute of Quantum Computing and the Perimeter Institute.
4) IQC, Free-space quantum key distribution, http://www.iqc.ca/laboratories/peg/free_space.php
Then they can share secrets with nobody able to spy on them unnoticed. They should do something to dramatize this capability! Unfortunately they don't actually have any secrets. So, they might need to make some up.
The really cool part, though, is that Scott helped me see that at least in principle, quantum computers could keep from drifting off course without the computation getting ruined by quantum entanglement with the environment. I had long been worried about this.
You see, to make any physical system keep acting "digital" for a long time, one needs a method to keep its time evolution from drifting off course. It's easiest to think about this issue for an old-fashioned, purely classical digital computer. It's already an interesting problem.
What does it mean for a physical system to act "digital"? Well, we like to idealize our computers as having a finite set of states; with each tick of the clock it jumps from one state to another in a deterministic way. That's how we imagine a digital computer.
But if our computer is actually a machine following the laws of classical mechanics, its space of states is actually continuous - and time evolution is continuous too! Physicists call the space of states of a classical system its "phase space", and they describe time evolution by a "flow" on this phase space: states move continuously around as time passes, following Hamilton's equations.
So, what we like to idealize as a single state of our classical computer is actually a big bunch of states: a blob in phase space, or "macrostate" in physics jargon.
For example, in our idealized description, we might say a wire represents either a 0 or 1 depending on whether current is flowing through it or not. But in reality, there's a blob of states where only a little current is flowing through, and another blob of states where a lot is flowing through. All the former states count as the "0" macrostate in our idealized description; all the latter count as the "1" macrostate.
Unfortunately, there are also states right on the brink, where a medium amount of current is flowing through! If our machine gets into one of these states, it won't act like the perfect digital computer it's trying to mimic. This is bad!
So, you should imagine the phase space of our computer as having a finite set of blobs in it - macrostates where it's doing something good - separated by a no-man's land of states where it's not doing anything good. For a simple 2-bit computer, you can imagine 4 blobs like this:
--------------------------
|??????????????????????????|
|??? ----- ?????? ----- ???|
|???| |??????| |???|
|???| 0 0 |??????| 0 1 |???|
|???| |??????| |???|
|??? ----- ?????? ----- ???|
|??????????????????????????|
|??? ----- ?????? ----- ???|
|???| |??????| |???|
|???| 1 0 |??????| 1 1 |???|
|???| |??????| |???|
|??? ----- ?????? ----- ???|
|??????????????????????????|
--------------------------
though in reality the phase space won't be 2-dimensional, but
instead much higher-dimensional.
Now, as time evolves for one tick of our computer's clock, we'd like these nice macrostates to flow into each other. Unfortunately, as they evolve, they sort of spread out. Their volume doesn't change - this was shown by Liouville back in the 1800s:
5) Wikipedia, Liouville's theorem (Hamiltonian), http://en.wikipedia.org/wiki/Liouville's_theorem_(Hamiltonian)
But, they get stretched in some directions and squashed in others. So, it seems hard for each one to get mapped completely into another, without their edges falling into the dangerous no-man's-land labelled "???".
We want to keep our macrostates from getting hopelessly smeared out. It's a bit like herding a bunch of sheep that are drifting apart, getting them back into a tightly packed flock. Unfortunately, Liouville's theorem says you can't really "squeeze down" a flock of states! Volume in phase space is conserved....
So, the trick is to squeeze our flock of states in some directions while letting them spread out in other, irrelevant directions.
The relevant directions say whether some bit in memory is a zero or one - or more generally, anything that affects our computation. The irrelevant ones say how the molecules in our computer are wiggling around... or the molecules of air around the computer - or anything that doesn't affect our computation.
So, for our computer to keep acting digital, it should pump out heat!
Here's a simpler example. Take a ball bearing and drop it into a wine glass. Regardless of its initial position and velocity - within reason - the ball winds up motionless at the bottom of the glass. Lots of different states seem to be converging to one state!
But this isn't really true. In fact, information about the ball's position and velocity has been converted into heat: irrelevant information about the motion of atoms.
In short: for a fundamentally analogue physical system to keep acting digital, it must dispose of irrelevant information, which amounts to pumping out waste heat.
In fact, Rolf Landauer showed back in 1961 that getting rid of one bit of information requires putting out this much energy in the form of heat:
kT ln(2)
where T is the temperature and k is Boltzmann's constant. That's not much - about 3 x 10-21 joules at room temperature! But, it's theoretically important.
What had me worried was how this would work for quantum computation. A bunch of things are different, but some should be the same. When we pump information - i.e., waste heat - from the computer into the environment, we inevitably correlate its state with that of the environment.
In quantum mechanics, correlations often take the form of "entanglement". And this is a dangerous thing. For example, if our quantum computer is in a superposition of lots of states where it's doing interesting things, and we peek at it to see which, we get entangled with it, and its state seems to "collapse" down to one specific possibility. We say it "decoheres".
Won't the entanglement caused by pumping out waste heat screw up the coherence needed for quantum computation to work its wonders?
I finally realized the answer was: maybe not. Yes, the quantum state of the computer gets entangled with that of the environment - but maybe if one is clever, only the irrelevant aspects of its state will get entangled: aspects that don't affect the computation. After all, it's this irrelevant information that one is trying to pump out, not the relevant information.
So, maybe it can work. I need to catch up on what people have written about this, even though most of it speaks the language of "error correction" rather than thermodynamics. Here are some things, including material Scott Aaronson recommended to me.
Gentle introductions:
6) Michael A. Nielsen and Isaac L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 2000.
7) John Preskill, Quantum computation - lecture notes, references etc. at http://www.theory.caltech.edu/people/preskill/ph229/
8) John Preskill, Fault-tolerant quantum computation, to appear in "Introduction to Quantum Computation", eds. H.-K. Lo, S. Popescu, and T. P. Spiller. Also available as quant-ph/9712048.
Chapter 7 of Preskill's lecture notes is about error correction.
This is a nice early paper on getting quantum computers to work despite some inaccuracy and decoherence:
9) Peter Shor, Fault-tolerant quantum computation, 37th Symposium on Foundations of Computing, IEEE Computer Society Press, 1996, pp. 56-65. Also available as quant-ph/9605011.
This more recent paper shows that in a certain model, quantum computation can be made robust against errors that occur at less than some constant rate:
10) Dorit Aharonov and Michael Ben-Or, Fault-tolerant quantum computation with constant error rate, available as quant-ph/9906129.
Here's a paper that assumes a more general model:
11) Barbara M. Terhal and Guido Burkard, Fault-tolerant quantum computation for local non-markovian noise, Phys. Rev. A 71, 012336 (2005). Also available as quant-ph/0402104.
Rolf Landauer was a physicist at IBM, and he discovered the result mentioned above - the "thermodynamic cost of forgetting" - in a study of Maxwell's demon. This is a fascinating and controversial subject, and you can learn more about it in this book of reprints:
12) H. S. Leff and Andrew F. Rex, editors, Maxwell's Demon: Entropy, Information and Computing, Institute of Physics Publishing, 1990.
I think Landauer's original paper is in here. He figured out why you can't get free energy from heat by using a little demon to watch the molecules and open a door to let the hot ones into a little box. The reason is that it takes energy for the demon to forget what it's seen!
Finally, on a somewhat different note, if you just want a great read on the interface between physics and computation, you've got to try this:
13) Scott Aaronson, NP-complete problems and physical reality, ACM SIGACT News, March 2005. Also available as quant-ph/0502072.
Can a soap film efficiently solve the traveling salesman problem by minimizing its area? If quantum mechanics were slightly nonlinear, could quantum computers solve NP problems in polynomial time? And what could quantum gravity computers do? Read and learn and the state of the art on puzzles like these.
At the Perimeter Institute I also had some great discussions with Laurent Freidel and his student Aristide Baratin. They have a new spin foam model that reproduces ordinary quantum field theory - in other words, particle physics in flat spacetime. It's not interesting as a model of quantum gravity - it doesn't include gravity! Instead, it serves as a convenient target for spin foam models that do include gravity: it should be the limit of any such model as the gravitational constant approaches zero.
14) Aristide Baratin and Laurent Freidel, Hidden quantum gravity in 4d Feynman diagrams: emergence of spin foams. Available as hep-th/0611042.
It's the sequel of this paper for 3d spacetime:
15) Aristide Baratin and Laurent Freidel, Hidden quantum gravity in 3d Feynman diagrams. Available as gr-qc/0604016.
Freidel, Kowalski-Glikman and Starodubtsev have also just come out with a paper carrying out some of the exciting project I mentioned in "week208":
16) Laurent Freidel, Jerzy Kowalski-Glikman and Artem Starodubtsev, Particles as Wilson lines in the gravitational field, available as gr-qc/0607014.
Their work is based on the MacDowell-Mansouri formulation of gravity. This is a gauge theory with gauge group SO(4,1) - the symmetry group of deSitter spacetime. DeSitter spacetime is a lot like Minkowski spacetime, but it has constant curvature instead of being flat. It's really just a hyperboloid in 5 dimensions:
{(w,x,y,z,t) : w2 + x2 + y2 + z2 - t2 = k2}
for some constant k. It describes an exponentially expanding universe, a lot like ours today. It's the most symmetrical solution of Einstein's equation with a positive cosmological constant. The cosmological constant is proportional to 1/k2.
When you let the cosmological constant approach zero, which is the same as letting k → ∞, DeSitter spacetime flattens out to Minkowski spacetime, and the group SO(4,1) contracts to the symmetry group of Minkowski spacetime: the Poincare group.
So, MacDowell-Mansouri gravity is similar to the formulation of gravity as gauge theory with the Poincare group as gauge group. I explained that pretty carefully back in "week176".
But, there's one way SO(4,1) is better than the Poincare group. It's a "simple" Lie group, so it has an inner product on its Lie algebra that's invariant under conjugation. This lets us write down the BF Lagrangian:
tr(B ^ F)
where tr is defined using the inner product, F is the curvature of an SO(4,1) connection A, and B is an so(4,1)-valued 2-form. Spin foam models of BF theory work really well:
17) John Baez, An introduction to spin foam models of BF theory and quantum gravity, in Geometry and Quantum Physics, eds. Helmut Gausterer and Harald Grosse, Lecture Notes in Physics, Springer-Verlag, Berlin, 2000, pp. 25-93. Also available as gr-qc/9905087.
So, the MacDowell-Mansouri approach is a natural for spin foam models. It's not that MacDowell-Mansouri gravity is a BF theory - but its Lagrangian is the BF Lagrangian plus extra terms. So, we can think of it as a perturbed version of BF theory.
There's also one way SO(4,1) is worse than the Poincare group. It's a simple Lie group - so it doesn't have a god-given "translation" subgroup the way the Poincare group does. The Poincare gauge theory formulation of general relativity requires that we treat translations differently from boosts and rotations. We can't do this in an SO(4,1) gauge theory unless we break the symmetry down to a smaller group: the Lorentz group, SO(3,1).
So, to get MacDowell-Mansouri gravity from SO(4,1) BF theory, we need to add extra terms to the Lagrangian that break the symmetry group down to SO(3,1). This isn't bad, just a bit sneaky.
The new paper by Freidel, Kowalski-Glikman and Starodubtsev is mainly about the SO(4,1) BF theory rather than full-fledged MacDowell-Mansouri gravity. They show that if you cut out curves in spacetime and couple them to the A field in the right way, they act like the worldlines of point particles. In particular, they have a mass and spin, and they trace out geodesics when their spin is zero. Spinning particles do something a bit fancier, but it's the right thing.
This generalizes some results for 3d gravity that I explained in detail back in "week232". It's nice to see it working in 4 dimensions too.
Back then I also explained something else about 4d BF theory: if you cut out surfaces in spacetime and couple them to the B field, they act like the worldsheets of 1-dimensional extended objects, which one might call strings. I don't think they're the wiggling stretchy strings that string theorists like; I think their equation of motion is different. But I should actually check! It's stupid; I should have checked this a long time ago.
Ahem. Anyway, it's really neat how particles couple to the A field and "strings" couple to the B field in BF theory.
This is vaguely reminiscent of how the A and B field form two parts of a "2-connection" - a gadget that lets you define parallel transport along curved and surfaces. You can read about 2-connections here:
18) John Baez and Urs Schreiber, Higher gauge theory, to appear in the volume honoring Ross Street's 60th birthday, available as math.DG/0511710.
The cool thing is that a pair consisting of an A field and a B field gives well-behaved parallel transport for curves and surfaces only if they satisfy an equation... which is implied by the basic equation of BF theory!
The above paper is a summary of results without proofs. Before one can talk about 2-connections, one needs to understand 2-bundles, which are a "categorified" sort of bundle where the fiber is not a smooth manifold but a smooth category. My student Toby Bartels recently finished writing an excellent thesis that defines 2-bundles and relates them to "gerbes" - another popular approach to higher gauge theory, based on categorifying the concept of "sheaf" instead of "bundle":
19) Toby Bartels, Higher Gauge Theory I: 2-bundles, available as math.CT/0410328.
The detailed study of 2-connections will show up in the next installment - a paper I'm writing with Urs Schreiber.
You can also see transparencies of some talks about this stuff:
20) John Baez, Alissa Crans and Danny Stevenson, Chicago lectures on higher gauge theory, available at http://math.ucr.edu/home/baez/namboodiri/
21) John Baez, Higher gauge theory, 2006 Barrett lectures, available at http://math.ucr.edu/home/baez/barrett/
It'll be lots of fun if higher gauge theory and the work relating MacDowell-Mansouri gravity to BF theory fit together and develop in some nontrivial direction. But the funny thing is, I don't how they fit together yet.
Here's why. In gauge theory, there's a famous way to get a number from a connection A and a loop. First you take the "holonomy" of A around the loop, and then you take the trace (in some representation of your gauge group) to get a number. This number is called a "Wilson loop".
This is an obvious way to define an action for a particle coupled to a connection A - at least if the particle moves around a loop. For example, it's this action that let us compute knot invariants from BF theory: you use the BF action for your fields, you use the Wilson loop as an action for your particle, and you compute the amplitude for your particle to trace out some knot in spacetime.
One might guess from the title "Particles as Wilson lines in the gravitational field" that this is the action Freidel and company use. But it's not!
Instead, they use a different action, which involves extra fields on the particle's worldline, describing its position and momentum. I explained a close relative of this action back in "week232", when I was coupling particles to 3d gravity.
The same funny difference shows up when we couple strings to the B field. In higher gauge theory you can define holonomies and Wilson loops using the A field, but you can also define "2-holonomies" and "Wilson surfaces" using both the A and B fields. The 2-holonomy describes how a string changes as it moves along a surface, just as the holonomy describes how a particle changes as it moves along a curve. If you have a closed surface you can take a "trace" of the 2-holonomy and get a number, which deserves to be called a "Wilson surface".
This is an obvious way to define an action for a string coupled to the A and B fields - at least if it traces out a closed surface. But, it's not the one Perez and I use! Why not? Because we were trying to do something analogous to what people did for particles in 3d gravity.
So, there's some relation between this "particles and strings coupled to 4d BF theory" business and the mathematics of higher gauge theory, but it's not the obvious one you might have guessed at first.
Mysteries breed mysteries. For more musings on these topics, try my talk at the Perimeter Institute:
22) John Baez, Higher-dimensional algebra: a language for quantum spacetime, colloquium talk at Perimeter Institute, available at http://math.ucr.edu/home/baez/quantum_spacetime/
John Baez wrote:Here's what Nathan Urban wrote:In fact, Rolf Landauer showed back in 1961 that getting rid of one bit of information requires putting out this much energy in the form of heat: kT ln(2)Ben Rubiak-Gould replied:It's easy to understand where this formula comes from. Getting rid of a bit means emitting one bit of entropy, which is k ln 2 in conventional units. The associated quantity of heat is ST = kT ln 2.Thanks; I should have said that.Landauer's analysis showing that "forgetting information" costs energy is still interesting, and it was surprising at the time. There had been a number of other analyses of why Maxwell's demon can't get you something for nothing, by Szilard and others, but none (I think) had focussed on the key importance of resetting the demon's memory to its initial state.
But it seems to me that you're conflating two different issues here. One is the cost of forgetting a bit, which only affects irreversible computation, and the other is the cost of keeping the computation on track, which affects reversible computation also. Landauer's formula tells you the former, but I don't think there's any lower bound on the latter.Not in principle: with a perfectly tuned dynamics, an analogue system can act perfectly digital, since each macrostate gets mapped perfectly into another one with each click of the clock. But with imperfect dynamics, dissipation is needed to squeeze each macrostate down enough so it can get mapped into the next - and the dissipation makes the dynamics irreversible, so we have to pay a thermodynamic cost.If I were smarter I could prove an inequality relating the "imperfection of the dynamics" (how to quantify that?) to the thermodynamic cost of computation, piggybacking off Landauer's formula.
John Baez wrote:[quantum computation] So, maybe it can work. I need to catch up on what people have written about this, even though most of it speaks the language of "error correction" rather than thermodynamics.A nice recent overview of some of this work can be found in the latest Physics Today:23) Sarma, Freedman, and Nayak, Topological quantum computation, Physics Today (July 2006).
In this approach, error-free computation is accomplished using topological quantum field theories, as topological theories are robust against local perturbations.
The article has some nice discussion of anyons, braidings, non-Abelian topological phases of condensed matter systems, etc. It speculates that the ν = 12/5 state of the fractional quantum Hall effect might support universal topological quantum computation (meaning that its braiding operators could realize any desired unitary transformation).
Here's my reply:
Long time no see, Nathan!The article in the latest Physics Today isn't free for nonsubscribers, but this is, and it seems to cover similar ground:Nathan Urban wrote:
John Baez wrote: >[quantum computation] >So, maybe it can work. I need to catch up on what people >have written about this, even though most of it speaks the >language of "error correction" rather than thermodynamics. A nice recent overview of some of this work can be found in the latest Physics Today (July 2006), in the article "Topological quantum computation" by Sarma, Freedman, and Nayak. (Nayak is at UCLA if you ever get out that way.)Thanks, I'll check that out.
I'm usually too lazy to drive into LA, but now that I'm in Shanghai, I thought I'd take the chance to visit Zhenghan Wang in the nearby city of Hangzhou and talk to him about topological quantum computation.
Wang and Freedman both work for "Project Q", aptly named after the Star Trek villain - it's Microsoft's project to develop quantum computers using nonabelian anyons:
24) Topological quantum computing at Indiana University, http://www.tqc.iu.edu/
The article has some nice discussion of anyons, braidings, non-Abelian topological phases of condensed matter systems, etc. It speculates that the ν=12/5 state of the fractional quantum Hall effect might support universal topological quantum computation (meaning that its braiding operators could realize any desired unitary transformation).Freedman, Larsen and Wang have already proved that certain versions of Chern-Simons theory support universal quantum computation:25) Michael Freedman, Michael Larsen, and Zhenghan Wang, A modular functor which is universal for quantum computation, available as quant-ph/0001108.
The fractional quantum Hall effect is supposedly described by Chern-Simons theory, so this is relevant. I don't know anything about the "ν = 12/5 state" of the fractional quantum Hall effect, but the folks at Project Q do want to use the fractional quantum Hall effect for quantum computation, and some people are looking for nonabelian anyons in the ν = 5/2 state:
26) Parsa Bonderson, Alexei Kitaev and Kirill Shtengel, Detecting non-abelian statistics in the ν = 5/2 fractional quantum Hall state, Phys. Rev. Lett. 96 (2006) 016803. Also available as cond-mat/0508616.
Apparently there's just one lab in the world that has the capability of producing these fractional quantum Hall states!
27) Charles Day, Devices based on the fractional quantum Hall effect may fulfill the promise of quantum computing, Physics Today (October 2005), also available at http://www.physicstoday.org/vol-58/iss-10/p21.html
It discusses both the ν = 12/5 and ν = 5/2 states.
Alas, I never managed to visit Zhenghan Wang in Hangzhou.
K. Eric Drexler writes:
Dear John,For an introduction to Drexler's plans for atomically-precise reversible computers, see:To continue a thread in Week 235:
John Baez wrote:
> [...] with a perfectly tuned dynamics, an analogue system > can act perfectly digital, since each macrostate gets > mapped perfectly into another one with each click of > the clock. But with imperfect dynamics, dissipation > is needed to squeeze each macrostate down enough so it > can get mapped into the next - and the dissipation > makes the dynamics irreversible, so we have to pay a > thermodynamic cost.Logically reversible computation can, in fact, be kept on track without expending energy and without accurately tuned dynamics. A logically reversible computation can be embodied in a constraint system resembling a puzzle with sliding, interlocking pieces, in which all configurations accessible from a given input state correspond to admissible states of the computation along an oriented path to the output configuration. The computation is kept on track by the contact forces that constrain the motion of the sliding pieces. The computational state is then like a ball rolling along a deep trough; an error would correspond to the ball jumping out of the trough, but the energy barrier can be made high enough to make the error rate negligible. Bounded sideways motion (that is, motion in computationally irrelevant degrees of freedom) is acceptable and inevitable.Keeping a computation of this sort on track clearly requires no energy expenditure, but moving the computational state in a preferred direction (forward!) is another matter. This requires a driving force, and in physically realistic systems, this force will be resisted by a "friction" caused by imperfections in dynamics that couple motion along the progress coordinate to motion in other, computationally irrelevant degrees of freedom. In a broad class of physically realistic systems, this friction scales like viscous drag: the magnitude of the mean force is proportional to speed, hence energy dissipation per distance travelled (equivalently, dissipation per logic operation) approaches zero as the speed approaches zero.
Thus, the thermodynamic cost of keeping a classical computation free of errors can be zero, and the thermodynamic cost per operation of a logically reversible computation can approach zero. Only Landauer's ln(2)kT cost of bit erasure is unavoidable, and the number of bits erased is a measure of how far a computation deviates from logical reversibility. These results are well-known from the literature, and are important in understanding what can be done with atomically-precise systems.
With best wishes,
Eric
28) K. Eric Drexler, Nanosystems: Molecular Machinery, Manufacturing, and Computation, John Wiley and Sons, New York, 1992.
The issue of heat dissipation in such devices is also studied here:
29) Ralph C. Merkle, Two types of mechanical reversible logic, Nanotechnology 4 (1993), 114-131. Also available at http://www.zyvex.com/nanotech/mechano.html
I need to think about this stuff more!
© 2006 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|