week240

October 22, 2006

This Week's Finds in Mathematical Physics (Week 240)

John Baez

I'm back from Shanghai, and classes are well underway now. For the last few weeks I'd been frantically preparing a talk for Stewart Brand's "Seminars About Long-Term Thinking", up in San Francisco. I talked about how we need to "zoom out" of our short-term perspective to understand the history of the earth's climate and what we're doing to it now:

1) John Baez, Zooming out in time, http://math.ucr.edu/home/baez/zoom/

There's a lot of tricky physics in this business. Consider, for example, this graph of cycles governing the Earth's precession, the obliquity of its orbit, and the eccentricity of its orbit:

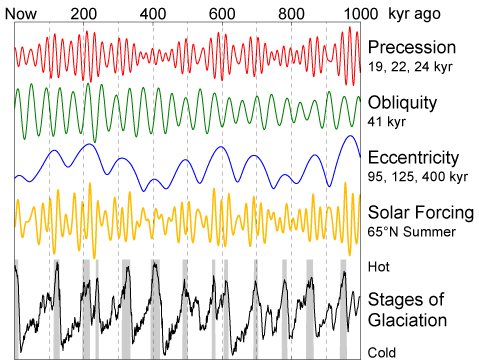
2) Wikipedia, Milankovitch cycles, http://en.wikipedia.org/wiki/Milankovitch_cycles

Here a "kyr" is a thousand years. The yellow curve combines information from all three of these cycles and shows the amount of solar radiation at 65 degrees north latitude. The bottom black curve shows the amount of glaciation. As Milankovitch's theory predicts, you can sort of see a correlation between the yellow and black curves - but it's nothing simple or obvious. One reason is the complex feedback mechanisms within the Earth's climate.

Here's a great place to read about this stuff:

3) Barry Saltzman, Dynamical Paleoclimatology: Generalized Theory of Global Climate Change, Academic Press, New York, 2002.

Anyway, now this talk is done, and I can focus more on teaching.

In my seminar this year, we're focusing on two topics: quantization and cohomology, and classical versus quantum computation. I'm trying out something new: not only are the notes available on the web, there's also a blog entry for each class, where you can ask questions, make comments and correct my mistakes!

4) John Baez, Fall 2006 seminars: Quantization and cohomology, and Classical versus quantum computation. Notes by Derek Wise, homeworks and blog entries available at http://math.ucr.edu/home/baez/qg-fall2006/

I hope more people blend teaching with blogging. It's not too much work if someone with legible handwriting takes notes and the lectures can actually be followed from the notes. You can use blogging to interactively teach people scattered all over the planet!

This week, James Dolan gave a talk on something he's been working on for a long time: games and cartesian closed categories. Lately he's been working with Todd Trimble, and they reproved some important results in a fun new way. Let me sketch the ideas for you....

Let's play a game. I have a set X in my pocket, and I'm not telling you what it is. Can you pick an element of X in a systematic way?

No, of course not: you don't have enough information. X could even be empty, in which case you're clearly doomed! But even if it's nonempty, if you don't know anything about it, you can't pick an element in a systematic way.

So, you lose.

Okay, let's play another game. Can you pick an element of

X^X

in a systematic way? Here A^B means the set of functions from B to A. So, I'm asking if you can pick a function from X to itself in a systematic way.

Yes! You can pick the identity function! This sends each element of X to itself:

x |→ x

You don't need to know anything about X to describe this function. X can even be empty.

So, you win.

Are there any other ways to win? No.

Now let's play another game. Can you pick an element of

X^{( X^X )}

in a systematic way?

An element in here takes functions from X to itself and turns them into elements of X. When X is the set of real numbers, people call this sort of thing a "functional", so let's use that term. A functional eats functions and spits out elements.

You can scratch your head for a while trying to dream up a systematic way to pick a functional for any set X. But, there's no way.

So, you lose.

Let's play another game. Can you pick an element of

(X^X)^{( X^X )}

in a systematic way?

An element in here eats functions and spits out functions. When X is the set of real numbers, people often call this sort of thing an "operator", so let's use that term.

Given an unknown set X, can you pick an operator in a systematic way? Sure! You can pick the identity operator. This operator eats any function from X to itself and spits out the same function:

f |→ f

Anyway: you win.

Are there any other ways to win? Yes! There's an operator that takes any function and spits out the identity function:

f |→ (x |→ x)

This is a bit funny-looking, but I hope you get what it means: you put in any function f, and out pops the identity function x |→ x.

This arrow notation is very powerful. It's usually called the "λ calculus", since when Church invented it in the 1930s, he wrote it using the Greek letter λ instead of an arrow: instead of

x |→ y

he wrote

λ x.y

But this just makes things more confusing, so let's not do it.

Are there more ways to win this game? Yes! There's also an operator called "squaring", which takes any function f from X to itself and "squares" it - in other words, does it twice. If we write the result as f², this operator is

f |→ f²

But, we can express this operator without using any special symbol for squaring. The function f is the same as the function

x |→ f(x)

so the function f² is the same as

x |→ f(f(x))

and the operator "squaring" is the same as

f |→ (x |→ f(f(x)))

This looks pretty complicated. But, it shows that our systematic way of choosing an element of

(X^X)^{( X^X )}

can still be expressed using just the λ calculus.

Now that you know "squaring" is a way to win this particular game, you'll immediately guess a bunch of other ways: "cubing", and so on. It turns out all the winning strategies are of this form! We can list them all using the λ calculus:

f |→ (x |→ x)

f |→ (x |→ f(x))

f |→ (x |→ f(f(x)))

f |→ (x |→ f(f(f(x))))

etc. Note that the second one is just a longer name for the identity operator. The longer name makes the pattern clear.

So far, all these methods of picking an element of (X^X)^{( X^X )} for an unknown set X can be written using the λ calculus. There are other sneakier ways. For example, there's the operator that sends functions with fixed points to the identity function, and sends functions without fixed points to themselves. It's an interesting challenge to figure out all these sneaky ways, but it's way too hard for me. So, from now on, just to keep things simple, let's only consider "systematic ways" that can be expressed using the λ calculus. To win one of my games, you need to use the λ calculus to pick an element of the set I write down.

So, let's play another game. Can you write down an element of

X ^{( X^{( X^X )} )}

using the λ calculus?

An element in here eats functionals and spits out elements of X. So, it's called a "functionalal" on X. At least that's what Jim calls it.

If I have an unknown set in my pocket, can you write down functionalal on this set using the λ calculus?

Yes! You need to dream up a recipe that takes functionals on X and turns them into elements of X. Here's one recipe: take any functional and evaluate it on the identity function, getting an element of x.

In λ calculus notation, this recipe looks like this:

f |→ f(x |→ x)

Can you think of other ways to win this game? I hope so: there are infinitely many! Jim and Todd figured out a systematic way to list them all.

Now let's play another game. Can you write down an element of

X^{(X^{(X^{(X^X)})})}

using the λ calculus? The parentheses are getting a little obnoxious by now, so let's adopt the convention that A^{B^C} is short for A^{(B^C)}, which lets us write the above expression as

X^{X^{X^{X^X}}}

A thing in here eats functionalals and spits out elements of X, so it's called a "functionalalal".

So, can you write down a functionalalal on an unknown set using the λ calculus?

The answer is no: you lose.

How about writing down an element of

((X^X)^{(X^X)})^{((X^X)^{(X^X)})}

using the λ calculus? Such a thing eats operators and spits out operators, so it's called an "operatorator".

The answer is yes: there are lots of ways to win this game. The real challenge is listing all of them! This is the sort of question Dolan and Trimble figured out the answer to - though as we'll see, they weren't the first.

In fact, instead of moving on to functionalators, operatorals, operatoralatorals, and so on, let me just tell you trick for instantly deciding which of all these games you can win.

You just take your game, like this:

((X^X)^{(X^X)})^{((X^X)^{(X^X)})}

and evaluate it by setting X = 0. If you get 0, there's no way to win. If you get 1, there's at least one way to win.

To use this trick, you need to know that

0⁰ = 1

This is something they don't teach in school! In analysis, X^Y can approach anything between 0 and 1 when X and Y approach 0 from above. So, teachers like to say 0⁰ is undefined. But X^X approaches 1 when X → 0. More importantly, in set theory, A^B stands for the set of functions from B to A, and the number of elements in this set is

|A^B| = |A|^|B|

When A and B are empty, there's just one function from B to A, namely the identity. So, for our purposes we should define 0⁰ = 1.

Consider the case of functionals, which are elements of X^{X^X}. If we evaluate this at X = 0 we get

0^0⁰ = 0¹ = 0

So, there are no functionals when X is the empty set. So, you can't pick a functional on a unknown set in any systematic way. That's why you lose when your game evaluates to 0. It's more interesting to prove that for games evaluating to 1, there's a way to win, using the λ calculus.

But we'd really like to understand all the ways to win using the λ calculus. And for this, Dolan and Trimble used the theory of holodeck games.

In Star Trek, the "holodeck" is a virtual reality environment where you can play various games:

On the holodeck, if you regret a move you made, you can back up to any earlier point in the game and make a new move.

Actually I'm deviating from the technical specifications of the holodeck on Star Trek, as explained here:

6) Wikipedia, Holodeck, http://en.wikipedia.org/wiki/Holodeck

So, if you're a Star Trek purist, it's better to imagine a video game where you can save your game at any state of play, and go back to these saved games whenever you want. And, you have to imagine being so paranoid that you always save your game before making a move. This allows games to go on forever, so we only say you have a winning strategy if you can win in a finite number of moves, no matter what the other player does.

To make this completely precise, we consider two-player games where the players take turns making moves. When a player can't make a move, they lose. Any such game can be written as a "game tree", like this:

     | \/ 
   \ | /
    \|/

In this example, the first player has three choices for her first move. If she picks the middle branch, the second player has one choice for his first move. Then the first player has one choice for her second move. Then the second player has no choice for his second move - so he loses.

So, in this particular example the second player has no winning strategy.

A cool thing about such a game is that we can take its game tree and turn it into an expression built from some variable X using products and exponentials. To do this, just put an X at each vertex of the tree except the root:

     X  X  X 
     |   \/ 
 X   X   X
  \  |  /
   X X X
    \|/

Then blow on the tree with a strong westerly wind, so strong that the branches blow away and only the X's are left:

        X   XX
   X   X   X
  X   X   X

This is just a way of writing an expression built from X using products and exponentials:

X^X X^{X^X} X^{X^XX}

Conversely, any such expression can be turned back into a tree, at least after we simplify it using these rules:

(AB)^C = A^C B^C

(A^B)^C = A^BC

For example, consider the set of operators:

(X^X)^{(X^X)}

If we simplify this, we get

X^{X X^X}

     X
  X X
 X

giving the tree

or in other words

      /
   \ /
    |

And here's a cool fact: if you take any expression built from X using products and exponentials, and evaluate it at X = 0, you can tell which player has a winning strategy for the game described by the corresponding tree! If you get 1, the second player has a winning strategy; if you get 0, they don't.

It's pretty easy to prove: try it.

But if you've been paying attention, you'll have noticed something weird.

I've told you two ways to get a game from any expression built from X using products and exponentials. First, the game of defining an element of the resulting set, using the λ calculus. Second, the game we get by turning this expression into a game tree, like I just did.

For both these games, you can decide if there's a winning strategy by evaluating the expression at X = 0.

But are they the same game? No! One is the holodeck version of the other!

Let's look at the familiar example of operators:

(X^X)^{(X^X)} = X^{X X^X}

This evaluates to 1 at X = 0. So, if we turn it into a tree

      /
   \ /
    |

we get a game where the second player has a winning strategy.

This game is not very exciting, but it becomes more exciting if you call it "The Lady or the Tiger". In this game, the first player has only one first move: he takes the second player to a room with two doors, corresponding to the two branches of the above tree.

Then it's the second player's turn.

If he opens the left door, a beautiful lady pops out and they instantly get married and live happily ever after. If he opens the right door, the first player opens a tiger cage. Then the tiger jumps out and eats the second player.

In this game, the second player has just one winning strategy: on his first move he should choose the left door.

Next look at the game of defining an element of

(X^X)^{(X^X)} = X^{X X^X}

using the λ calculus. We've seen there are infinitely many strategies for winning this:

f |→ (x |→ x)

f |→ (x |→ f(x))

f |→ (x |→ f(f(x)))

f |→ (x |→ f(f(f(x))))

and so on. These correspond to 2nd-player winning strategies for the holodeck version of The Lady or the Tiger.

What are these strategies?

One is just to play the game and win by choosing the left door.

Another is to choose the right door - and then, just when the tiger is about to eat you, back up and choose the left door!

Another is to choose the right door - and then, just when the tiger is about to eat you, back up and choose... the right door!

Then, when the tiger is about to devour you again, back up again, and this time choose the left door.

And so on: for each n, there's a strategy where you choose the right door n times before wising up and choosing the left door.

Now, if you want a really nice math project, ponder the pattern relating all these strategies to the corresponding λ calculus expressions:

f |→ (x |→ x)

f |→ (x |→ f(x))

f |→ (x |→ f(f(x)))

f |→ (x |→ f(f(f(x))))

Then, figure out how to prove that for any 2-person game, say:

     | \/ 
   \ | /
    \|/

there's a 1-1 correspondence between winning second-person strategies for the holodeck verson of this game and ways of using the λ calculus to define elements of the corresponding set:

X^X X^{X^X} X^{X^XX}

Apparently this result goes back to work of Hyland and Ong in the early 1990s. Dolan rediscovered the idea, and Trimble and he have recently worked out a new proof.

If you get stuck proving this result yourself, first try these notes from Dolan's talk, for some hints:

7) James Dolan, Holodeck strategies and cartesian closed categories, lecture at UCR, notes by John Baez, Oct. 19, 2006, available at http://math.ucr.edu/home/baez/qg-fall2006/f06week03b.pdf

Then try Trimble's more rigorous, technical treatment, and the original paper by Hyland and Ong:

8) Todd Trimble, Holodeck games and CCCs, available at http://math.ucr.edu/home/baez/trimble/holodeck.html

9) Martin Hyland and C.-H. Luke Ong, On full abstraction for PCF, Information and Computation, 163 (2000), 285-408. Also available at ftp://ftp.comlab.ox.ac.uk/pub/Documents/techpapers/Luke.Ong/pcf.ps.gz

Dolan's talk also explains some other fun stuff, like how to multiply and exponentiate games. So, if you read these notes, you'll learn how to play

chess × go

and

chess^go

at least after chess and go have been "improved" so games never last forever and the last player able to make a move wins.

But, if you're planning to study this stuff, I'd better admit right now that Dolan and Trimble make heavy use of the relation between the λ calculus and cartesian closed categories.

A category is "cartesian" if it has finite products - or in other words, binary products and a terminal object. It's "cartesian closed" if it also has exponentials. All these terms are carefully defined in the week 2 and week 3 notes of my classical versus quantum computation course, so let me just illustrate them with an example: the category of sets. Here the product A × B of two sets A and B is their usual Cartesian product. The exponential A^B is the set of functions from B to A. Any 1-element set is a terminal object.

Dolan and Trimble don't really talk about an unknown set X, as I did above. What they really study is the "free cartesian closed category on one object x", which I like to call CCC[x]. Any object in CCC[x] is built from the object x by means of binary products, exponentials and the terminal object. For example, we have objects like this:

x¹ 1^{x^x} (x x)^{x 1 x^{x^x}}

where I've omitted the times symbols for products.

However, every object is isomorphic to one in "tree form". For example, the above object is isomorphic to

x x^{x x^{x^x}} x^{x x^{x^x}}

which we can draw as a tree:

   x     x
   |    /
 x x x x 
  \| |/  
 x x x   
  \|/

Dolan and Trimble consider the set of elements of any object in CCC[x], where an "element" is a morphism from the terminal object, e.g.

f: 1 → x x^{x x^{x^x}} x^{x x^{x^x}}

And, they show these elements are in 1-1 correspondence with second-player winning strategies for the holodeck version of the game whose tree is constructed as above.

If we pick any set X, the universal property of CCC[x] gives a functor

F: CCC[x] → Set

This maps elements of any object in CCC[x] to elements of the corresponding object in Set:

F(f): 1 → X X^{X X^{X^X}} X^{X X^{X^X}}

So, the element f gives a systematic way of picking elements of any set built from any arbitrary set X using finite products and exponentials.

By the way, in a cartesian closed category, there's a 1-1 correspondence between morphisms

f: B → A

and elements

f: 1 → A^B

So, one can use games to describe all the objects and morphisms in the free cartesian closed category on one object! One can also describe composition of morphisms using games. In short, there's a complete description of CCC[x] in terms of games.

Now let me give you some references on cartesian closed categories, the λ calculus, categorical semantics, and games. It's an interesting network of subjects.

Categorical semantics was born in Lawvere's celebrated 1963 thesis on algebraic theories:

10) F. William Lawvere, Functorial Semantics of Algebraic Theories, Dissertation, Columbia University, 1963. Also available at http://www.tac.mta.ca/tac/reprints/articles/5/tr5abs.html

Semantics deals with theories and their models. Dual to the concept of semantics is the concept of "syntax", which deals with proofs. In the case of algebraic theories, the syntax was studied before Lawvere in the subject called "universal algebra":

11) Stanley Burris and H.P. Sankappanavar, A Course in Universal Algebra, available at http://www.math.uwaterloo.ca/~snburris/htdocs/ualg.html

Lawvere modernized universal algebra by realizing that an algebraic theory is just a cartesian category, and a model is a product-preserving functor from this theory into Set or some other cartesian category - hence his thesis title, "Functorial Semantics". I explained this in much more detail back in week200.

The relevance of all this to computer science becomes visible when we note that a proof in universal algebra can be seen as a rudimentary form of computation. The "input" of the computation is a set of assumptions, while the "output" is the equation to be proved.

Treating proofs as computations may seem strained, but it becomes less so when we move to richer formalisms which allow for more complex logical reasoning. One of best-known of these is the λ calculus, invented by Church and Kleene in the 1930s as a model of computation. Any function computable by the λ calculus is also computable by a Turing machine, and according to the Church-Turing thesis these are all the functions computable by any sort of systematic process. Moreover, computations in the λ calculus can actually be seen as proofs.

The usefulness of this way of thinking was brought out in Landin's classic paper:

12) P. Landin, A correspondence between ALGOL 60 and Church's λ-notation, Comm. ACM 8 (1965), 89-101, 158-165.

This began a long and fruitful line of research - see for example this:

13) H. Barendregt, The Lambda Calculus, its Syntax and Semantics, North-Holland, 1984.

The power of the λ calculus is evident in the textbook developed for MIT's introductory course in computer science, which is available online:

14) H. Abelson, G. J. Sussman and J. Sussman, Structure and Interpretation of Computer Programs, available at http://www-mitpress.mit.edu/sicp/

It cites pioneers like Haskell Curry, and it even has a big "λ" on the cover!

Students call it "the wizard book", because the cover also features a picture of a wizard. It's used at over 100 colleges and universities, and it has spawned a semi-mythical secret society called The Knights of the Lambda Calculus, whose self-referential emblem celebrates the ability of the λ calculus to do recursion:

In 1980, Lambek made a great discovery:

15) Joachim Lambek, From lambda calculus to Cartesian closed categories, in To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, eds. J. P. Seldin and J. Hindley, Academic Press, 1980, pp. 376-402.

He showed that just as algebraic theories can be regarded as cartesian categories, theories formulated in the λ calculus can be regarded as cartesian closed categories (or CCCs, for short).

Lambek's discovery introduced a semantics for the λ calculus, since it lets us to speak of "models" of theories formulated in the λ calculus, just as we could for algebraic theories. In computer programming, the importance of a model is that it gives a picture of what a program actually accomplishes. A model in the category of Sets, for example, sends any program to an actual function between sets.

There's no way to list all the interesting references to CCCs and the λ-calculus, but here are some online places to get going on them, starting out easy and working up to the harder ones. This Wikipedia article is quite good:

16) Wikipedia, Lambda calculus, available at http://en.wikipedia.org/wiki/Lambda_calculus These blog entries by Mark Chu-Carroll are lots of fun - just the kind of readable, informal exposition I aspire to:

17) Mark Chu-Carroll, Lambda calculus, available at http://goodmath.blogspot.com/2006/06/lamda-calculus-index.html

Mark Chu-Carroll, Category theory, available at http://scienceblogs.com/goodmath/goodmath/category_theory/

These go deeper:

18) Peter Selinger, Lecture notes on the lambda calculus, available at http://www.mscs.dal.ca/~selinger/papers.html#lambdanotes

and deeper:

19) Phil Scott, Some aspects of categories in computer science, available at http://www.site.uottawa.ca/~phil/papers/handbook.ps

and here's a classic:

20) Joachim Lambek and Phil Scott, Introduction to Higher Order Categorical Logic, volume 7 of Cambridge Studies in Advanced Mathematics, Cambridge U. Press, 1986.

Dolan and Trimble are far from the first to study the relation between games and categories. In the 1970s, Conway invented a wonderful theory of games and surreal numbers:

21) John H. Conway, On Numbers and Games, Academic Press, New York, 1976. Second edition: A. K. Peters, Wellesley, Massachusetts, 2001.

22) Elwyn Berlekamp, John H. Conway, Richard Guy, Winning Ways, vols. 1-2, Aadmic Press, New York, 1982. Second edition, vols. 1-4, A. K. Peters, Wellelsey, Massachusetts, 2001-2004.

23) Dierk Schleicher and Michael Stoll, An introduction to Conway's games and numbers, available as math.CO/0410026.

In 1977, Joyal modified Conway's work a bit and related it explicitly to category theory:

24) André Joyal, Remarques sur la theorie des jeux a deux personnes, Gazette des Sciences Mathematiques du Quebec, Vol I no 4 (1977), 46-52.

For an online version in English, try:

25) André Joyal, trans. Robin Houston, Remarks on the theory of two-person games, 2003. Available at http://www.ma.man.ac.uk/~rhouston/Joyal-games.ps

I don't know the subsequent history very well - I'm no expert on any of this stuff! - but by 1990 Martin Hyland was giving lectures on Conway games and logic. In 1992, Andreas Blass published an influential paper on "game semantics" for logic, where propositions are interpreted as games and winning strategies are proofs:

26) Andreas R. Blass, Game semantics and linear logic, Annals of Pure and Applied Logic 56 (1992), 183-220.

Then came these important papers:

27) Samson Abramsky and Radha Jagadeesan, Games and full completeness for multiplicative linear logic, Journal of Symbolic Logic, 59 (1994), 543 - 574. Also available at http://citeseer.ist.psu.edu/564168.html

28) Martin Hyland and C.-H. Luke Ong, Fair games and full completeness for multiplicative linear logic without the MIX-rule, available at http://citeseer.ist.psu.edu/hyland93fair.html

According to Samson Abramsky,

After these results, it was clear that the most notorious issue in programming language semantics, the "full abstraction problem for PCF", was in range. Remarkably enough, two different teams:

Abramsky, Jagadeesan and Malacaria

Hyland and Ong

produced really quite different constructions which yielded in the end the same result: a synthetic construction of the fully abstract model. (The technical issue in both cases was how to accomodate the linear exponentials, i.e. the possibility to copy and delete inputs to functions. It turned out there are two very different approaches which can be taken. The HO approach (also independently found by Hanno Nickau, incidentally) is quite related to the ideas of the Lorenzen school, but, crucially, done compositionally. The AJM approach is related to the Geometry of Interaction - but takes the quite demanding step of making an honest CCC out of it.)
After that, the next key step was to see that the whole space of programming languages and computational features opened up to a game theoretic analysis in a very systematic way, by varying the conditions on strategies. This step was taken by myself and my students, and has led to a substantial further development. More recently, Luke Ong, Dan Ghica, Andrzej Murawski and myself have developed algorithmic game semantics, as a basis for compositional program analysis and verification, and - in Luke and Andrzej's hands - as a beautiful meeting point between semantics and algorithmics.
There have of course been many other developments too, and many people have contributed. There have been recent workshops on these topics, e.g. in Seattle as part of the Federated Logic Conference in August.

"PCF" is a souped-up version of the typed λ calculus that allows one to do arithmetic and full-fledged computation. Here are the papers on PCF mentioned above:

29) Samson Abramsky, R. Jagadeesan, and P. Malacaria, Full abstraction for PCF, Information and Computation, 163 (2000), 409-470. Available at http://web.comlab.ox.ac.uk/oucl/work/samson.abramsky/pubs.html

30) Martin Hyland and C.-H. Luke Ong, On full abstraction for PCF, In Information and Computation 163 (2000), 285-408.

Luke Ong has also written other papers using game theory to study the λ calculus:

31) A. D. Ker, H. Nickau, and C.-H. Luke Ong, A universal innocent game model for the Böhm tree λ theory, in Computer Science Logic: Proceedings of the 8th Annual Conference on the EACSL Madrid, Spain, September 1999, LNCS Volume 1683, Springer-Verlag, 1999, pp. 405-419.

32) A. D. Ker, H. Nickau, and C.-H. Luke Ong, Innocent game models of untyped λ-calculus, Theoretical Computer Science, 272 (2002), 247-292.

For a good introduction to all this work, try these:

33) Robin Houston, Categories of Games, M.Sc. thesis, U. Manchester, 2003. Available at http://www.cs.man.ac.uk/~houstorx/msc.pdf

Robin Houston, Mathematics of Games, continuation report, U. Manchester, 2004. Available at http://www.cs.man.ac.uk/~houstorx/continuation.pdf

Finally, for more on categories, intuitionistic logic, and linear logic, see "week227".

Addenda: I thank Samson Abramsky, James Dolan, Dominic Hughes, Tom Payne, Esa Peuha and Vaughn Pratt for helpful corrections. When I wrote the first version of this Week's Finds, I was ignorant of work before Dolan and Trimble's that also described the free cartesian closed category on one object in terms of games. In addition to Abramsky's corrections (some of which are above), I was gently set straight by Dominic Hughes, who has permitted me to attach this post of his from the category theory mailing list:

This "backtracking game" characterisation has been known since around
'93-'94, in the work of Hyland and Ong:

  M. Hyland and L. Ong. On full abstraction for PCF.  Information and
  Computation, Volume 163, pp. 285-408, December 2000. [Under review for
  6 years!]
  ftp://ftp.comlab.ox.ac.uk/pub/Documents/techpapers/Luke.Ong/pcf.ps.gz

(PCF is an extension of typed λ calculus.)  My D.Phil. thesis
extended the λ calculus (free CCC) characterisation to second-order,
published in:

  Games and Definability for System F. Logic in Computer Science, 1997
  http://boole.stanford.edu/~dominic/papers/

To characterise the free CCC on an arbitrary set {Z,Y,X,...} of
generators (rather than a single generator, as you discuss), one simply
adds the following Copycat Condition:

  (*) Whenever first player plays an occurrence of X, the second player
      must play an occurrence of X.

[Try it: see how X → Y → X has just one winning strategy.] Although the
LICS'97 paper cited above appears to be the first place the Copycat
Condition appears in print, I like to think it was already understood at
the time by people working in the area.  Technically speaking, winning
strategies correspond to η-expanded β-normal forms.  See pages 5-7 of
my thesis for an informal description of the correspondence.

It sounds like you've reached the point of trying to figure out how
composition should work.  Proving associativity is fiddly.  Hyland and
Ong give a very elegant treatment, via a larger CCC of games in which
both players can backtrack.  The free CCC subcategory is carved 
out as the so-called innocent strategies.  This composition is 
almost identical to that presented by Coquand in:

  A semantics of evidence for classical arithmetic.  Thierry Coquand.
  Proceedings of the CLICS workshop, Aarhus, 1992.

Dominic

PS A game-theoretic characterisation with an entirely different flavour
(winning strategies less "obviously" corresponding to η-long β-normal
forms) is:

  Abramsky, S., Jagadeesan, R. and Malacaria, P., Full Abstraction for
  PCF.  Info. & Comp. 163 (2000), 409-470.
  http://web.comlab.ox.ac.uk/oucl/work/samson.abramsky/pcf.pdf
  [Announced concurrently with Hyland-Ong, around '93-'94.]

On a different subject, James Dolan had this to say:

you describe holodeck strategies for "lady or tiger" where you take back "just when the tiger is about to eat you", but that's not the way it works. you take back just _after_ the tiger has eaten you.
(i guess that this is partially because of your lack of experience with computer games with a "saved game" feature. typically you die in the game and the computer plays some sort of funeral or at least funereal music; then you're taken to the reincarnation gallery where you select one to return to from your catalog of previous lives. or something like that.)

In the first version of this Week's Finds I claimed that all systematic ways of picking an element of (X^X)^{(X^X)} could be defined using the λ calculus. I was disabused of this notion by Vaughan Pratt, who wrote:

Hi, John,
In "week240", you said
  The moral of this game is that all systematic methods for picking
  an element of (X^X)^(X^X) for an unknown set X can be written
  using the λ calculus.
What is unsystematic about the contagious-fixpoint functional? This is the functional that maps those functions that have any fixpoints to the identity function (the function that makes every element a fixpoint) and functions without fixpoints to themselves (thus preserving the absence of fixpoints). It's a perfectly good functional that is equally well defined for all sets X, its statement in no way depends on X, and conceptually the concept of contagious fixpoints is even intuitively natural, but how do you write it using the λ calculus?
Many more examples in this vein at JPAA 128, 33-92 (Pare and Roman, Dinatural numbers, 1998). The above is the case K = {0} of Freyd's (proper) class of examples.
Vaughan

Here Pratt uses "functional" to mean what I was calling an "operator".

For more discussion, go to the n-Category Café.

Unlike chess or astrology, mathematics has the curious property of being an intellectual game that really matters. - Rudy Rucker