




|
 
|

|
I've been working too hard, and running around too much, to write This Week's Finds for a while. A bunch of stuff has built up that I want to explain. Luckily I've been running around explaining stuff - higher gauge theory, and tales of the dodecahedron.
This weekend I went to Baton Rouge. I was invited to Louisiana State University by Jorge Pullin of loop quantum gravity fame, and I used the opportunity to get a look at LIGO - the Laser Interferometry Gravitational-Wave Observatory!
I described this amazing experiment back in "week189", so I won't rehash all that. Suffice it to say that there are two installations: one in Hanford Washington, and one in Livingston Louisiana. Each consists of two evacuated tubes 4 kilometers long, arranged in an L shape - here's the one in Livingston:

Laser beams bounce back and forth between mirrors suspended at the ends of the tubes, looking for tiny changes in their distance that would indicate a gravitational wave passing through, stretching or squashing space. And when I say "tiny", I mean smaller than the radius of a proton! This is serious stuff.
Jorge drove me in his SUV to Livingston, a tiny town about 20 minutes from Baton Rouge. While he runs the gravity program at Louisiana State University, which has links to LIGO, he isn't officially part the LIGO team. His wife is. When I first met Gabriela Gonzalez, she was studying the Brownian motion of torsion pendulums. The mirrors in LIGO are hung on pendulums made of quartz wire, to minimize the effect of vibrations. But, the random jittering of atoms due to thermal noise still affects these pendulums. She was studying this noise to see its effect on the accuracy of the experiment.
This was way back when LIGO was just being planned. Now that LIGO is a reality, she's doing data analysis, helping search for gravitational waves produced by pairs of neutron stars and/or black holes as they spiral down towards a sudden merger. Together with an enormous pageful of authors, she helped write this paper, based on data taken from the "first science run" - the first real LIGO experiment, back in 2002:
1) The LIGO Scientific Collaboration, Analysis of LIGO data for gravitational waves from binary neutron stars, Phys. Rev. D69 (2004), 122001. Also available at gr-qc/0308069.
She's one of the folks with an intimate knowledge of the experimental setup, who keeps the theorists' feet on the ground while they stare up into the sky.
On the drive to Livingston, Jorge pointed out the forests that surround the town. These forests are being logged:

I asked him about this - when I last checked, the vibrations from falling trees were making it impossible to look for gravitational waves except at night! He said they've added a "hydraulic external pre-isolator" to shield the detector from these vibrations - basically a super-duper shock absorber:

Now they can operate LIGO day and night.
I also asked him how close LIGO had come to the sensitivity levels they were seeking. When I wrote "week189", during the first science run, they still had a long way to go. That's why the above paper only sets upper limits on neutron star collisions within 180 kiloparsecs. This only reaches out to the corona of the Milky Way - which includes the Small and Large Magellanic Clouds. We don't expect many neutron star collisions in this vicinity: maybe one every 3 years or so. The first science run didn't see any, and the set an upper limit of about 170 per year: the best experimental upper limit so far, but definitely worth improving, and nowhere near as fun as actually seeing gravitational waves.
But Jorge said the LIGO team has now reached its goals: they should be able to see collisions out to 15 megaparsecs! By comparison, the center of the Virgo cluster is about 20 megaparsecs away. In fact, they should already be able to see about half the galaxies in this cluster.
They're now on their seventh science run, and they'll keep upping the sensitivity in future projects called "Enhanced LIGO" and "Advanced LIGO". The latter should see neutron star collisions out to 300 megaparsecs:
2) Advanced LIGO, http://www.ligo.caltech.edu/advLIGO/
When we arrived at the gate, Jorge spoke into the intercom and got us let in. Our guide, Joe Giaime, was running a bit a late, so we walked over and looked at the interferometer's arms, each of which stretched off beyond sight, 2.5 kilometers of concrete tunnel surrounding the evacuated piping - the world's largest vacuum facility:

Schoolkids have been invited to paint pictures on some of these pipes:

One can tell this is the South. The massive construction caused pools of water to form in the boggy land near the facility, and these pools then attracted alligators. These have been dealt with firmly. The game hunters who occasionally fired potshots at the facility were treated more forgivingly: instead of feeding them to the alligators, the LIGO folks threw a big party and invited everyone from the local hunting club. Hospitality works wonders down here.
The place was pretty lonely. During the week lots of scientists work here, but this was Saturday, and on weekends there's just a skeleton crew of two. There's usually not much to do now that the experiment is up and running. As Joe Giaime later said, there have been no "Jodie Foster moments" like in the movie Contact, where the scientists on duty suddenly see a signal, turn on the suspenseful background music, and phone the President. There's just too much data analysis required to see any signal in real time: data from both Livingston and Hanford is sent to Caltech, and then people grind away at it. So, about the most exciting thing that happens is when the occasional tiny earthquake throws the laser beam out of phase lock.
When Joe showed up, I got to see the main control room, which is dimly lit, full of screens indicating noise and sensitivity levels of all sorts - and even some video monitors showing the view down the laser tube:

This is where the people on duty hang out - you can see those video monitors on top:

One of them had brought his sons, in a feeble attempt to dispose of the huge supply of Halloween candy that had somehow collected here.
I also got to see a sample of the 400 "optical baffles" which have been installed to absorb light spreading out from the main beam before it can bounce back in and screw things up. The interesting thing is that these baffles and their placement were personally designed by Kip Thorne and some other godlike LIGO figure. Moral: unless they've gone soft, even bigshot physicists like to actually think about physics now and then, not just manage enormous teams.
But overall, there was surprisingly little to see, since the innermost workings are all sealed off, in vacuum. The optics are far more complicated than my description - "a laser bouncing between two suspended mirrors" - could possibly suggest. But, all I got to see was a chart showing how they work:
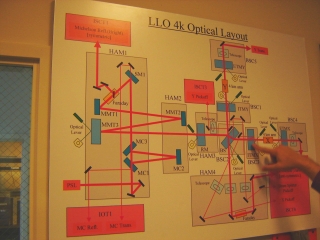
Oh well. I'm glad I don't need to understand this stuff in detail. It was fun to get a peek.
By the way, I wasn't invited to Louisiana just to tour LIGO and eat beignets and alligator sushi. My real reason for going there was to talk about higher gauge theory - a generalization of gauge theory which studies the parallel transport not just of point particles, but also strings and higher-dimensional objects:
3) John Baez, Higher gauge theory, http://math.ucr.edu/home/baez/highergauge
This is a gentler introduction to higher gauge theory than my previous talks, some of which I inflicted on you in "week235". It explains how BF theory can be seen as a higher gauge theory, and briefly touches on Urs Schreiber's work towards exhibiting Chern-Simons theory and 11-dimensional supergravity as higher gauge theories. The webpage has links to more details.
I was also travelling last weekend - I went to Dartmouth and gave this talk:
4) John Baez, Tales of the Dodecahedron: from Pythagoras through Plato to Poincare, http://math.ucr.edu/home/baez/dodecahedron/
It's full of pictures and animations - fun for the whole family!
I started with the Pythagorean fascination with the pentagram, and how you can use the pentagram to give a magical picture proof of the irrationality of the golden ratio.
I then mentioned how Plato used four of the so-called Platonic solids to serve as atoms of the four elements - earth, air, water and fire - leaving the inconvenient fifth solid, the dodecahedron, to play the role of the heavenly sphere. This is what computer scientists call a "kludge" - an awkard solution to a pressing problem. Yes, there are twelve constellations in the Zodiac - but unfortunately, they're arranged quite differently than the faces of the dodecahedron.
This somehow led to the notion of the dodecahedron as an atom of "aether" or "quintessence" - a fifth element constituting the heavenly bodies. If you've ever seen the science fiction movie The Fifth Element, now you know where the title came from! But once upon a time, this idea was quite respectable. It shows up as late as Kepler's Mysterium Cosmographicum, written in 1596.
I then went on to discuss the 120-cell, which gives a way of chopping a spherical universe into 120 dodecahedra.
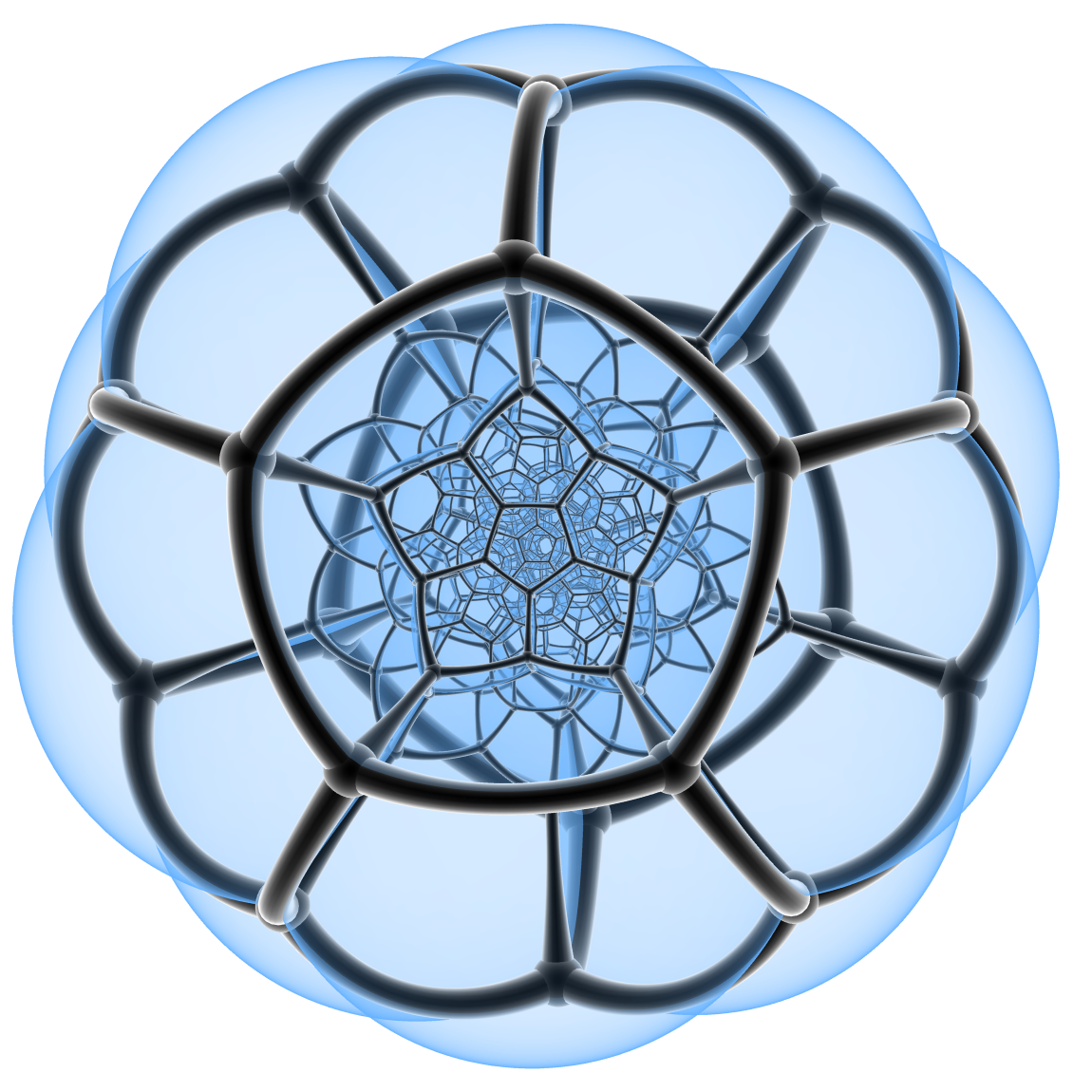
This leads naturally to the Poincare homology sphere, a closely related 3-dimensional manifold made by gluing together opposite sides of one dodecahedron.
The Poincare homology sphere was briefly advocated as a model of the universe that could explain the mysterious weakness of the longest-wavelength ripples in the cosmic background radiation - the ripples that only wiggle a few times as we scan all around the sky:
5) J.-P. Luminet, J. Weeks, A. Riazuelo, R. Lehoucq, and J.-P. Uzan, Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background, Nature 425 (2003), 593. Also available as astro-ph/0310253.
The idea is that if we lived in a Poincare homology sphere, we'd see several images of each very distant point in the universe. So, any ripple in the background radiation would repeat some minimum number of times: the lowest-frequency ripples would be suppressed.
Alas, this charming idea turns out not to fit other data. We just don't see the same distant galaxies in several different directions:
6) Neil J. Cornish, David N. Spergel, Glenn D. Starkman and Eiichiro Komatsu, Constraining the topology of the universe, Phys. Rev. Lett. 92 (2004) 201302. Also available as astro-ph/0310233.
For a good review of this stuff, see:
7) Jeffrey Weeks, The Poincare dodecahedral space and the mystery of the missing fluctuations, Notices of the AMS 51 (2004), 610-619. Also available at http://www.ams.org/notices/200406/fea-weeks.pdf
In the abstract of my talk, I made the mistake of saying that the regular dodecahedron doesn't appear in nature - that instead, it was invented by the Pythagoreans. You should never say things like this unless you want to get corrected!
Dan Piponi pointed out this dodecahedral virus:
8) Liang Tang et al, The structure of Pariacoto virus reveals a dodecahedral cage of duplex RNA, Nature Structural Biology 8 (2001), 77-83. Also available at http://www.nature.com/nsmb/journal/v8/n1/pdf/nsb0101_77.pdf
The first black line is 100 angstroms long (10-8 meters), while the second is 50 angstroms long.
Garett Leskowitz pointed out the molecule "dodecahedrane", with 20 carbons at the vertices of a dodecahedron and 20 hydrogens bonded to these:
9) Wikipedia, Dodecahedrane, http://en.wikipedia.org/wiki/Dodecahedrane
This molecule hasn't been found in nature yet, but chemists can synthesize it using reactions like these:
10) Robert J. Ternansky, Douglas W. Balogh and Leo A. Paquette, Dodecahedrane, J. Am. Chem. Soc. 104 (1982), 4503-4504.
11) Leo A. Paquette, Dodecahedrane - the chemical transliteration of Plato's universe (a review), Proc. Nat. Acad. Sci. USA 14 part 2 (1982), 4495-4500. Also available at http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=346698
So, there's probably a bit somewhere in our galaxy.
Of course, what I meant was that people didn't come up with regular dodecahedra after seeing them in nature - that instead, the Pythagoreans dreamt them up, possibly after seeing pyrite crystals that look sort of similar. These crystals are called "pyritohedra".
But, even here I made a mistake. The Pythagoreans seem not to have been the first to discover the dodecahedron. John McKay told me that stone spheres with Platonic solids carved on them have been found in Scotland, dating back to around 2000 BC!
13) Michael Atiyah and Paul Sutcliffe, Polyhedra in physics, chemistry and geometry, available as math-ph/0303071.
14) Dorothy N. Marshall, Carved stone balls, Proc. Soc. Antiq. Scotland, 108 (1976/77), 40-72. Available at http://ads.ahds.ac.uk/catalogue/library/psas/
Indeed, stone balls with geometric patterns on them have been found throughout Scotland, and occasionally Ireland and northern England. They date from the Late Neolithic to the Early Bronze age: 2500 BC to 1500 BC. For comparison, the megaliths at Stonehenge go back to 2500-2100 BC.
Nobody knows what these stone balls were used for, though the article by Marshall presents a number of interesting speculations.
The pyritohedron is interesting in itself, so before I turn to some really fancy math, let me talk a bit about this guy. Since pyrite is fundamentally a cubic crystal, the pyritohedron is basically made out of little cubic cells, as shown here:
12) Steven Dutch, Building isometric crystals with unit cells, http://www.uwgb.edu/dutchs/symmetry/isometuc.htm
It has 12 pentagonal faces, orthogonal to these vectors:
(2,1,0) (2,-1,0) (-2,1,0) (-2,-1,0) (1,0,2) (-1,0,2) (1,0,-2) (-1,0,-2) (0,2,1) (0,2,-1) (0,-2,1) (0,-2,-1)You can see how this works by going here:
13) mindat.org, Pyrite, http://www.mindat.org/min-3314.html
If your webbrowswer can handle Java, go to this webpage and click on "Pyrite no. 3" to see a rotating pyritohedron. Then, while holding your left mouse button down when the cursor is over the picture of the pyritohedron, type "m" to see the vectors listed above.
Why "m"? These vectors are called "Miller indices". In general, Miller indices are outwards-pointing vectors orthogonal to the faces of a crystal; we can use them to classify crystals.
The Miller indices for the pyritohedron have a nice property. If you think of these 12 vectors as points in space, they're the corners of three 2×1 rectangles: a rectangle in the xy plane, a rectangle in the xz plane, and a rectangle in the yz plane.
These points are also corners of an icosahedron! It's not a regular icosahedron, though. It's probably the "pseudoicosahedron" shown in Steven Dutch's site above:
Apparently iron pyrite can also form a pseudoicosahedron - see "Pyrite No. 7" on the mindat.org website above. Does anyone have actual photos?
To get the corners of a regular icosahedron, we just need to replace the number 2 by the golden ratio Φ = (√ 5 + 1)/2:
(Φ,1,0) (Φ,-1,0) (-Φ,1,0) (-Φ,-1,0) (1,0,Φ) (-1,0,Φ) (1,0,-Φ) (-1,0,-Φ) (0,Φ,1) (0,Φ,-1) (0,-Φ,1) (0,-Φ,-1)Now our rectangles are golden rectangles:
Since the pseudoicosahedron does a cheap imitation of this trick, with the number 2 replacing the golden ratio, the number 2 deserves to be called the "fool's golden ratio". I thank Carl Brannen for explaining this out to me!
The regular docahedron is "dual" to the regular icosahedron: the vertices of the icosahedron are Miller indices for the dodecahedron. Similarly, I bet the pyritohedron is dual to the pseudoicosahedron.
So, we could call the pyritohedron the "fool's dodecahedron", and the pseudoicosahedron the "fool's icosahedron". Fool's gold may have fooled the Greeks into inventing the regular dodecahedron, by giving them an example of a fool's dodecahedron.
As pointed out by Noam Elkies and James Dolan, there is a sequence of less and less foolish dodecahedra whose faces have normal vectors
(B,A,0) (B,-A,0) (-B,A,0) (-B,-A,0) (A,0,B) (-A,0,B) (A,0,-B) (-A,0,-B) (0,B,A) (0,B,-A) (0,-B,A) (0,-B,-A)where A and B are the nth and (n+1)st Fibonacci numbers, respectively. As n → ∞, these dodecahedra approach a regular dodecahedron in shape, because the ratio of successive Fibonacci numbers approaches the golden ratio.
When A = 1 and B = 2, we get the fool's dodecahedron, since only a fool would think 2/1 is the golden ratio.
However, this is not the most foolish of all dodecahedra! The case A = 1 and B = 1 gives the rhombic dodecahedron, which doesn't even have pentagonal faces:
14) Wikipedia, Rhombic dodecahedron, http://en.wikipedia.org/wiki/Rhombic_dodecahedron
So, the rhombic dodecahedron deserves to be called the "moron's dodecahedron" - at least for people who think it's actually a regular dodecahedron.
But actually, even this dodecahedron isn't the dumbest. The Fibonacci numbers start with 0:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
So, even more foolish is the case A = 0 and B = 1. Here our 12 vectors reduce to just 6 different ones:
(1,0,0) (1,-0,0) (-1,0,0) (-1,-0,0) (0,0,1) (-0,0,1) (0,0,-1) (-0,0,-1) (0,1,0) (0,1,-0) (0,-1,0) (0,-1,-0)These are normal to the faces of a cube. So, the cube deserves to be called the "half-wit's dodecahedron": it doesn't even have 12 faces, just 6.
Moving in the direction of increasing wisdom, we can consider the case A = 2, B = 3. This gives a dodecahedron which is closer to regular than the pyritohedron. And, apparently it exists in nature! It shows up as number 12 in this list of crystals:
15) Ian O. Angell and Moreton Moore, Projections of cubic crystals, section 4: The diagrams, http://www.iucr.org/education/pamphlets/12/full-text
They also call this guy a pyritohedron, so presumably some pyrite forms these less foolish crystals! You can compare it with the A = 1, B = 2 case here:
16) Ian O. Angell and Moreton Moore, Projections of cubic crystals, Graphical index of figures, http://www.iucr.org/education/pamphlets/12/graphical-index
The A = 1, B = 2 pyritohedron is figure 9, while the A = 2, B = 3 pyritohedron is figure 12. It's noticeably better!
Let me wrap up by mentioning a fancier aspect of the dodecahedron which has been intriguing me lately. I already mentioned it in "week230", but in such a general setting that it may have whizzed by too fast. Let's slow down a bit and enjoy it.
The rotational symmetries of the dodecahedron form a 60-element subgroup of the rotation group SO(3). So, the "double cover" of the rotational symmetry group of the dodecahedron is a 120-element subgroup of SU(2). This is called the "binary dodecahedral group". Let's call it G.
The group SU(2) is topologically a 3-sphere, so G acts as left translations on this 3-sphere, and we can use a dodecahedron sitting in the 3-sphere as a fundamental domain for this action. This gives the 120-cell. The quotient SU(2)/G is the Poincare homology sphere!
But, we can also think of G as acting on C2. The quotient C2/G is not smooth: it has an isolated singular coming from the origin in C2. But as I mentioned in "week230", we can form a "minimal resolution" of this singularity. This gives a holomorphic map
p: M → C2/G
where M is a complex manifold. If we look at the points in M that map to the origin in C2/G, we get a union of 8 Riemann spheres, which intersect each other in this pattern:
/\ /\ /\ /\ /\ /\ /\
/ \ / \ / \ / \ / \ / \ / \
/ \ \ \ \ \ \ \
/ / \ / \ / \ / \ / \ / \ \
\ \ / \ / \ / \ / \ / \ / /
\ \ \ \ \ /\ \ \ /
\ / \ / \ / \ / \ \ \ / \ /
\/ \/ \/ \/ / \/ \ \/ \/
/ \
\ /
\ /
\ /
\/
Here I've drawn linked circles to stand for these intersecting
spheres, for a reason soon to be clear. But, already you can
see that we've got 8 spheres corresponding to the dots in this
diagram:
o----o----o----o----o----o----o
|
|
o
where the spheres intersect when there's an edge between the
corresponding dots. And, this diagram is the Dynkin diagram for
the exceptional Lie group E8!
I already mentioned the relation between the E8 Dynkin diagram and the Poincare homology sphere in "week164", but now maybe it fits better into a big framework. First, we see that if we take the unit ball in C2, and see what points it gives in C2/G, and then take the inverse image of these under
p: M → C2/G,
we get a 4-manifold whose boundary is the Poincare homology 3-sphere. So, we have a cobordism from the empty set to the Poincare homology 3-sphere! Cobordisms can be described using "surgery on links", and the link that describes this particular cobordism is:
/\ /\ /\ /\ /\ /\ /\
/ \ / \ / \ / \ / \ / \ / \
/ \ \ \ \ \ \ \
/ / \ / \ / \ / \ / \ / \ \
\ \ / \ / \ / \ / \ / \ / /
\ \ \ \ \ /\ \ \ /
\ / \ / \ / \ / \ \ \ / \ /
\/ \/ \/ \/ / \/ \ \/ \/
/ \
\ /
\ /
\ /
\/
Second, by the "McKay correspondence" described in "week230", all this stuff also works for
other Platonic solids! Namely:
If G is the "binary octahedral group" - the double cover of the rotational symmetry group of the octahedron - then we get a minimal resolution
p: M → C2/G
which yields, by the same procedure as above, a cobordism from the empty set to the 3-manifold SU(2)/G.
This cobordism can be described using surgery on this link:
/\ /\ /\ /\ /\ /\
/ \ / \ / \ / \ / \ / \
/ \ \ \ \ \ \
/ / \ / \ / \ / \ / \ \
\ \ / \ / \ / \ / \ / /
\ \ \ \ /\ \ \ /
\ / \ / \ / \ \ \ / \ /
\/ \/ \/ / \/ \ \/ \/
/ \
\ /
\ /
\ /
\/
which encodes the Dynkin diagram of E7:
o----o----o----o----o----o
|
|
o
And, if G is the "binary tetrahedral group" - the double
cover of the rotational symmetry group of the tetrahedron - then a
minimal resolution
p: M → C2/G
yields, by the same procedure as above, a cobordism from the empty set to the 3-manifold SU(2)/G. This cobordism can be described using surgery on this link:
/\ /\ /\ /\ /\
/ \ / \ / \ / \ / \
/ \ \ \ \ \
/ / \ / \ / \ / \ \
\ \ / \ / \ / \ / /
\ \ \ /\ \ \ /
\ / \ / \ \ \ / \ /
\/ \/ / \/ \ \/ \/
/ \
\ /
\ /
\ /
\/
which encodes the Dynkin diagram of E6:
o----o----o----o----o
|
|
o
I don't fully understand this stuff, that's for sure. But, I
want to. The Platonic solids are still full of mysteries.
Addenda: Someone with the handle "Dileffante" has found another nice example of the dodecahedron in nature - and even in Nature:
While perusing a Nature issue I found this short notice on a paper, and I remembered that in your talk (which I saw online) you mentioned that the dodecahedron was not found in nature. Now I see in "week241" that there are some things dodecahedral after all, but nevertheless, I send this further dodecahedron which was missing there.Dodecahedrane is a molecule built from carbon and hydrogen - a bit different from an "atomic cluster" of the sort discussed here. It's a matter of taste whether that's important, but I bet these gold-palladium nanoparticles occur in nature, while dodecahedrane seems to be unstable.Nature commented in issue 7075:
15) The complete Plato, Nature 439 (26 January 2006), 372-373.
According to Plato, the heavenly ether and the classical elements - earth, air, fire and water - were composed of atoms shaped like polyhedra whose faces are identical, regular polygons. Such shapes are now known as the Platonic solids, of which there are five: the tetrahedron, cube, octahedron, icosahedron and dodecahedron. Microscopic clusters of atoms have already been identified with all of these shapes except the last.The article is in:Now, researchers led by José Luis Rodríguez-López of the Institute for Scientific and Technological Research of San Luis Potosé in Mexico and Miguel José-Yacamén of the University of Texas, Austin, complete the set. They find that clusters of a gold-palladium alloy about two nanometres across can adopt a dodecahedral shape.
16) Juan Martín Montejano-Carrizales, José Luis Rodríguez-López, Umapada Pal, Mario Miki-Yoshida and Miguel José-Yacamán, The completion of the Platonic atomic polyhedra: the dodecahedron, Small, 2 (2006), 351-355.
Here's the abstract:
Binary AuPd nanoparticles in the 1-2 nm size range are synthesized. Through HREM imaging, a dodecahedral atomic growth pattern of five fold axis is identified in the round shaped (85%) particles. Our results demonstrate the first experimental evidence of this Platonic atomic solid at this size range of metallic nanoparticles. Stability of such Platonic structures are validated through theoretical calculations.Either there is some additional value in the construction, or the authors (and Nature editors) were unaware of dodecahedrane.
My friend Geoffrey Dixon contributed these pictures of Platonic life forms:
They look a bit like Ernst Haeckel's pictures from his book "Kunstformen der Natur" (artforms of nature).
Finally, here's a really important addendum: in March 2009, Lieven le Bruyn discovered that the ancient Scots did not carve stone balls to look like Platonic solids! The whole story is something between a hoax and a series of misunderstandings:
17) Lieven le Bruyn, The Scottish solids hoax, from his blog neverendingbooks, March 25, 2009, http://www.neverendingbooks.org/index.php/the-scottish-solids-hoax.html
18) John Baez, Who discovered the icosahedron?, talk at the Special Session on History and Philosophy of Mathematics, 2009 Fall Western Section Meeting of the AMS, November 7, 2009. Available at http://math.ucr.edu/home/baez/icosahedron/
You can read a bunch of freewheeling discussions triggered by this Week's Finds at the n-Category Café.
© 2006 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|